Савельвев А.Я. Основы информатики

Подождите немного. Документ загружается.

2.3.

Основные понятия алгебры логики

Таблица 2.2

функция

/о

Ло

/и

/l!

/п

/|.

/|,

(К)

,Т|

1(1

Примечание

Уо — абсолютная ложь

.Х|

-Т;

{конъюнкция)

л:,

jt2

(запрет

Х2

)

XjX2 V

х,Х2

(переменная л,)

л,Д2 (запрет Л|)

Л|Л2

х^х2

= Х2

(переменная Л;)

JC|

Х2

(сложение по модулю 2)

Jf| V

Х2

(дизъюнкция)

jC|

Х2

(функция Пирса)

.Т|

= Х2

(равнозначность)

д,3с2

л,

jtj =

Х2

(переменная Дз )

Х2

-»

Л,

(импликация)

I|j(j

J,j(j = J| (переменная i,)

JC|

-»

(импликация)

^\1н (функция Шеффера)

/j — абсолютная истина

От дизъюнкции следует отличать функцию /б(Х|, Хз), которая называ-

е1ся функцией сложения по модулю 2 {функцией исключительное ИЛИ) и

являе|ся исгиииой, когда истинны или х,, или Xj, в отдельности. Условное

обозначение этой функции f(,{x^, Хз) = х, ©Xj.

Конъюнкция (логическое умножение) — функция /i(x,,X2), которая

истинна только тогда, когда и х,, и Xj истинны. Конъюнкцию часто назывануг

также функцией И; условно обозначают так: /j (х,, Xj)

== Xj

х-^

л Xj.

Пример

2.1.

Имеются два высказывания: «Завтра будет холодная погода», «Завтра пой-

дет сне1)>.

/ипъюикция 1гих высказываний — новое высказывание: «Завтра будет холодная погода

или нойдеч cnei» Соединигельный союз, который образовал новое предложение, — ИЛИ.

Коньюнкция образуется следующим образом: «Завтра будет холодная погода и пойдет

снег» Эю высказывание образовано с помощью союза И.

Штрих Шеффера — функция fxi^{x^,Xj), которая ложна только тогда,

когда Х| и Xj истинны. Условное обозначение функции Шеффера:

2 Автомат как основной элемент информационных систем

/]4(Х],Х2)-

xjx2 . Немецкий математик Д. Шеффер на основе этой функ-

ции создал алгебру, названную алгеброй Шеффера.

Функция Пирса {Вебба) — функция /^{х^, д^;)' которая истинна только

тогда, когда л, и х^ ложны. Условное обозначение этой функции:

Математики Ч. Пирс и Д. Вебб, независимо друг от друга изучавшие

свойства этой функции, создали алгебру, названную алгеброй Пирса (Вебба).

Импликация — функция

/,з(^{,

^2)» которая ложна тогда и только югда,

когда д:, истинной Xj ложно. Условное обозначение:

J\->.{x^,X2)

х^

—>•

.YJ

Все логические функции, приведенные в таблице 2.2, — элеме^ггарные

функции.

Две функции равносильны друг другу, если принимают на всех воз-

можных наборах переменных одни и те же значения:

/,(:г,,д:з,...,д:„) = Уз(д:,,д:2'---'^Л-

Булевы переменные могут быть действительными или фиктивными.

Переменная х, Эе«с/пбы/пельна, если значение функции /{х,,..., ж,,...,-v,,)

изменяется при изменении л,. Переменная х, фиктивна, если значение

функции f{x^,...,x,,...,x^) не изменяется при изменении х,.

Пример логической функции от трех переменных представлен в таб-

лице 2.3.

Из таблицы видно, что переменные л, и Xj —действительные, а пере-

менная ^3 —фиктивная, так как /{х,,^2,0) = /(x,,^2J) Д^я всех наборов

Таблица 2.3

.т,

Jtj

/(-I|.-«2.'j)

/^,."2.-'])

Использование фиктивных функций дает возможность сокращать или

расширять количество переменных для логических функций.

Так как число значений переменных х, ограничено, то можно опреде-

лить количество функций

от любого числа переменных «;

Л^

- 2 .

23 Основные понятия алгебры логики

Рассмотрим некоторые практические примеры использования алгебры

логики.

Пример 2.2. В школе произошла неприятная история: разбито окно в одном из классов.

Подозревают четырех учеников: Леню, Диму, Толю и Мишу. При опросе каждый из детей

сделал по три заявления:

Леия:

1) я не виноват— Л,;

2) я не подходил к окну — Л;;

3) Миша uiaei. кю разбил, — Л, ,

Дима:

1) стекло разбил не я — Д, ;

2) с Ми!пеГ1 я не был знаком до 1юс-|ур|ления в школу — Д^;

3)')10 сделал 1оля— Д^ ,

Толя:

1) я не виповаг— Г, ;

2) -Jto сделал Миша — Г;:

3) Дима говорит неправду, утверждая, что я разбил окно, — Tj.

Миша:

i) я не впмопаг — М, :

2) сгекло разбил Леия— М;;

3) Дима может поручиться замени, так как знает меня со дня рождения,— Mj.

В дальнейшем все признали, что одно нз трех заявлений является неверным. Это приго-

дится при посгроепин более сложных формул, поскольку показания каждого ученика в це-

лом исгиниы только при условии, что два заявления истинны, а одно ложно. Используя эле-

меигарные логические-<|)ункции, можно описать показания всех учеников в таком виде:

Л =

П^П^И^

+ Л,Л2Лз

Л.Л^Л,;

д = Д1Д2Д3 + ДДзД^ + Д1Д2Дз;

Т = Т|ТДз+Т|Т2Тз + Т,ТзТз;

и = MiMjM, + M,MjM3 + М,МзМ, .

lenepb ociaeicfl решить эту систему уравнений и определить, какие показания истинны.

Для эюги надо упростить выражения, используя аксиомы.

Рассмотрим третье уравнение. По условию, Т, =Тз, а значит, Т, =Тз, но Т,?, =0,

Т|1|

= 1', или

= Т|Т2. Поэтому оно верно тогда, когда Т, =1; Тг =0. Значит, Толя не

виноват и Миша не виноват. Отсюда следует, что Д, ложно, т. е. Дз =

(Дз = 1). Следо-

вате1п,н(>, Д =

J\i)\2)\%

•

Отсюда Д, = I; Дз = i. Дима не виноват.

Д, противоположно Mj, т. е. Дз = Мз. Значит. М^ =

или М = МрМ^Мз. Оно верно

только гогда, когда М, = I; М, =

1 •

Ответ стекло разбил Леня.

2 Автомат как основной элемент информационных систем

Пример 2.3. Предположим,

что

имеется система кондиционирования воздуха для

по-

мешенич,

где

установлена ЭВМ, состоящая

из

двух кондиционеров малой

большой

моипюсчи

работающая при таких условиях: кондиционер малой мошности аключаося.

если icMiieparypa воздуха

помещении достигает 19° С

;

конди[[ионср большой мошносги

включается, ecjrn температура воздуха достигает 22° С (малый кондиционер при этом

от-

К]ночас1СЯ), оба кондиционера включаются при температуре воздуха 30° С

ilycib информация

температуре воздуха поступает

ог

датчиков, когорыс сраба-

тывают

ори

достижении темпера

уры соответственно

19, 22,

30° С , Каждый

из них

датчиков выдает входную ин(|)ормаии10 для устройства управления коидиииопсрамч

Первые три датчика определяют рабочие режимы,

и их

можно Г1релстави1ь

как

входы

управляющею автомата. Используя двоичный алфавит для задания состояний да пика

(О

— нет

сигнала

достижении заданного уровня тем11ерат>ры,

1 —

ectb сигнал),

(|(ункниопиронамис системы управления кондиционерами можно описать следующим

oGpajoM

--,

~г

'-,

(1)2

'"|

Здесь

г, -

СИ1

пал да[чика, срабагывающего

при f

~19°С;

г, -

(), ес;ги iCMnepaTvpa

меньше !9°t';

г, =

если температура равна или болыне

19°С; Zj

—да1чпк, cpaGai

[>i-

ваюший 1гри

/ =

22°С. Гз-О.если /<22°С, Z2=l fipn

> 22° С

; Zj

—датчик. сраба1ы-

вающий При

= 3(ГС;

г, =0

ггри /<30°С,

при /

> 30° С

; (0| и Ш; —

cooiBeici-

мсшю

СИ1

палы управления ма]юмощпым

мошиым К(»идициоперами (tu

коилициоиер выключен,

I —-кондиционер включен).

!<1блииа описр>1вает функционирование системы управле1шя без нарушений работы.

Впервые теория Дж. Ьуля была применена П. С. Эренфесюм к ппшииу

контактных цепей (1910 г.). Возможность описания переключательных

схем с помощью логических формул оказалась весьма ценной гю двум при-

чинам. Во-первых, с помощью формул удобнее проверять работу схем. Во-

вторых, задание условий работы любой переключательной схемы в виде

формул упрощает процесс построения самой переключательной схемы, так

как оказалось, что существует ряд эквивалентных преобразований, в ре-

зультате которых логические формулы упрощаются. При описании irepe-

ключательных схем замкнутое состояние контакта принимается за истин-

ное высказывание, а разомкнутое — за ложное, поэтому последовагельиое

соединение контактов можно рассматривать как функцию И, а параллель-

ное — как функцию ИЛИ.

2 4 Свойства элементарных функций алгебры логики

Использование логических функций оказалось особенно полезным для

описания работы логических элементов ЭВМ.

2,4.

Свойства элементарных функций алгебры логики

Из таблицы 2.2 видно, что элементарные функции типа отрицания,

дизъюнкции, Шеффера, Пирса, импликации и т. д. находятся в определен-

ной связи друг с другом. Рассмотрим эти связи и свойства исходных функ-

ций.

Конъюнкция, дизъюнкция, отрицание (функции И,

ИЛИ,

НЕ). Используя основные положения алгебры логики, нетрудно убе-

диться в cnpaBe4J!HB0CTH следующих восьми аксиом. Пусть х — некоторая

логическая неременная. Гогда

.Y ^ JC, что означает возможность исключения из логического выра-

жения всех чле1юв, имеющих двойное отрицание, заменив их исходной ве-

личиной;

2. х + х^х-.хх = х — правила подобных преобразований позволяют

сокращай, длину Jюгичecкиx выражений;

г +

т :

= I;

5. .тО-О;

6. X

• 1

- X ;

XT - О;

Н. X i х^1 .

Дизъюнкция и конъюнкция обладают рядом свойств, аналогичных

свойствам обычных арифметических операций сложения и умножения:

1) свойсмн) ассоциативности (сочетательный закон):

Д", +(,Гз + Х,) = (^1 +

-'^2)'*'^3'

Х^(Х2Х^)

(Х^Х2)Х^

;

2) свойство коммутативности (переместительный закон):

Х| + Х2 -=Х2 +Х, , X,.V2

=^2^1^

3) СВОЙС1ВО дистрибутивности (распределительный закон):

для коньюнкции относительно дизъюнкции

&(х2 +x^) = (Xi&x2) +

(Xi&Xj^);

для дизъюнкции относительно конъюнкции

X, 4- Х2Ху =(X^+X2)& (Х^

+Xj,).

Автомат

как

основной элемент информационных

систем

Свойство дистрибутивности фактически определяет правила раскры-

тия скобок или взятия в скобки логических выражений.

Справедливость указанных свойств легко доказывается с помощью

вышеизложенных аксиом.

Докажем, например, что

ДГ|

Ж,.Гз

(Х|

+ X, ) &

(ДГ|

+Ху).

в самом деле, (х,+.г,ХдГ| + дг,) =

ДГ|ДГ|

дГ|Дг,

ДГ|ДГ,

дг,.1,

.v,

+ хух, +

+ .V|J:, +

JCJX,

- Х,(1 +^2 +

x-f,)^-

XjXy

= д:, + ^3^:3 •

Аналогично можно доказать и другие законы.

Несложно установить правильность соотношений, извес!ных как ншо-

иы де Моргана:

' ' ' _J (2.1)

Из законов де Моргана вытекают следствия:

^ (2.2)

с помощью которых появляется возможность выражагь копъюпкцто че-

рез дизъюнкцию и отрицание njrn дизъюнкцию через конъюнкцию и от-

рицание.

Законы де Моргана и следствия из них справедливы для любого

KOJHI-

чества переменных:

X, 4-х, +... + Х = X,

&...&д:„,

\ I _" _

_" (2.3)

X^Xi

..-Х,,

= X| 4- ^2

+•..-+•

Х„ .

Для логических функций устанавливаются соотношения, известные

как законы поглощения:

Х< т

^ Xi,

\ ' (2.4)

X^{x^+X^)=Xf.

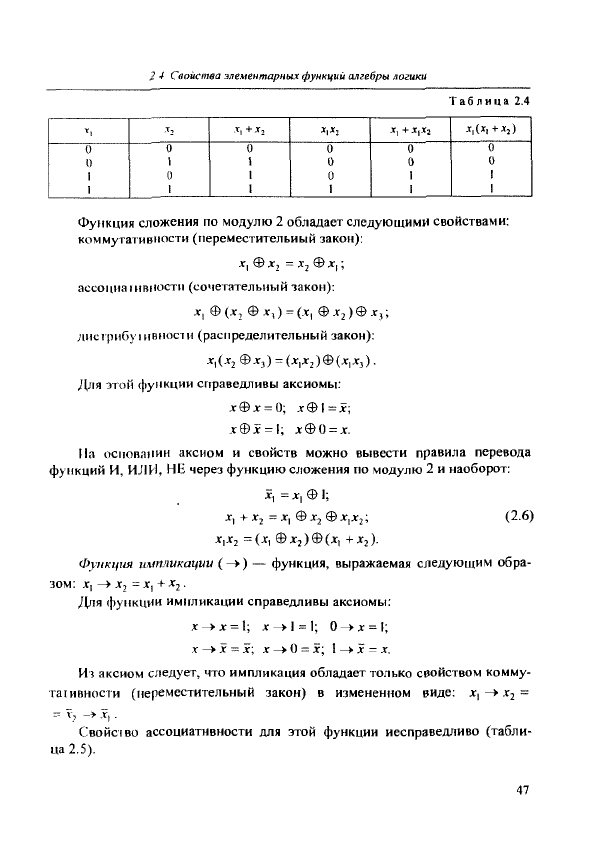
в таблице 2.4 показана справедливость законов поглощения.

Функция слолсения по модулю 2 (исключительное ИЛИ) — функция,

выражаемая следующим образом:

Xj ФХ2 =

Х^Х2

+X,X2

~{Х^

^^2){^\

-+-.^2)

• (2-5)

2 4 Свойства элементарных функций алгебры логики

Таблица 2.4

г,

х^

.т,

+ jr^

дг,д:2

JC|

Х^Х2

Jt|(^l+-<2)

функция сложения по модулю 2 обладает следующими свойствами:

коммутативности (переместительиый закон):

Xj Ш

д:,

= Л'2 Ш

Х^

ассоциа1ивиостн (сочетательный закон):

д:,

Ф(д:, ®х,)

(х^

®Х2)®х,;

лисгри6у1нвнос1И (распределительный закон):

х^(х-2

®Xj,)

(x^x-i)®(x^x-^).

Д/гя этой функции справедливы аксиомы:

x®x

f3;

х®\=х;

х®х^\; x®{i

Па основании аксиом и свойств можно вывести правила перевода

функций И, ИЛИ, НЕ через функцию сложения по модулю 2 и наоборот:

>1;

(2.6)

Х^

^2 — ^1

У? ^2 Ш Xj ^2 i

Х^Х2

(X|

® Х2)® (X| + Х2

Функция импликации (->) — функция, выражаемая следующим обра-

зом: Xf ^^ Xj ~

Х^

-i-

Х2

Для (функции импликации справедливы аксиомы:

х-*х

= \;

д:->1 =

0->x = l;

^>х ~х; X —>0 = х; I —>х - X.

Из аксиом следует, что импликация обладает только свойством комму-

ташвноети (иереместительныи закон) в измененном виде: х,-> д^з =

= Ь ->

^^1 •

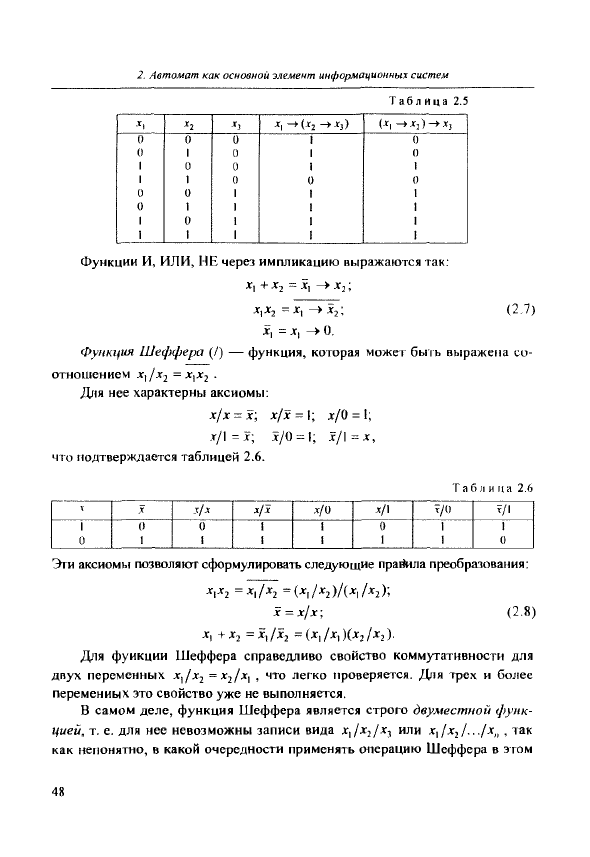
Свойс1во ассоциативности для этой функции несправедливо (табли-

ца 2.5).

Автомат как основной элемент информационных систем

Таблица 2.5

Jt,

J^)

X, ->(_Г2 ->-rj)

(ДГ|

->.rj)->jr,

функции и, или, НЕ через импликацию вь!ражаются так;

Х\ т" Лт

—

Х\

"~~т

Хл ,

Функция Шеффера (/)

отношением x^/xj =^^1^:2 •

Для нее характерны аксиомы:

х/х

х;

xjx -

x(Q =

-r/l - х; х/0 -

J/I - х

что подтверждается таблицей 2.6.

Xi Xj

—

"~~т

Xj ^

.X,

Х|

—>

функция, которая може! быгь выражена

(2-7)

х/0

г/1)

Эти

аксиомы позволяют сформулировать следующие прайила преобразования:

x^X2

=xjxj ={xjxj)l{xjx2)\

х/х; (2.8)

Х,

Д^т

•^i

/Xj

*™

\Х\ IХ\

jyXj

/Х2 )•

Для функции Шеффера справедливо свойство коммутативности для

двух переменных xjx2 ^Xjjx^ , что легко проверяется. Для трех и более

переменных это свойство уже не выполняется.

В самом деле, функция Шеффера является строго двуместной функ-

цией, т. е. для нее невозможны записи вида xjxj/x-^ или x^jxjl...jx^^ , так

как непонятно, в какой очередности применять операцию Шеффера в этом

2.4. Свойства элементарных функций алгебры логики

выражении. Следовательно, очередность применения операции Шеффера

должна указываться с помощью скобок, как, например,

((xjx^)lx,)lx^ или (X|/Xj)/(X3/*4)-

Э1И выводы подтверждаются также тем, что свойства ассоциативности

и дистрибутивности для функции Шеффера несправедливы. В самом деле,

справедливость свойства ассоциативности ведет к тому, что должны быть

равны выражения (xjx2)/x, и xj^x^jx^).

Применяя правила преобразования к этим выражениям, получаем

-Г] j{X2lx-^) = X^ i- Xj -f Д^з •

Проверка равнозначности этих выражений представлена в таблице 2.7.

-^i

)

Х,Х2

х-^х.

х,х^

+ jtj

i,+v,

Следовательно, функции (х,/х2)/х, и xJ(x2Xi) не равны, значит,

функция Шеффера не обладает свойством ассоциативности в случае трех

переменных, что можно распространить и на «и» переменных.

/1ля функции Шеффера свойство дистрибутивиости означает, что

должны быть равны две функции: xJ{x2X,) и (д:|/х2)/(*|/*з). Преобразуем

эти функции, используя аксиому J =

дг/1:

'|/(*2^з) = ^|

+*2^3

=(*|

+*2К*|

+*з)-(^1/*2Х*|/*з) =

(х,/(х2/т^/{х,/\))

(x,/(xjl

))/(х,

/(х,/\

))/1;

(,xJX2)(xJx,) = (x,X2)(XfX,) =

XfX2

+ Х^Х, = Х,(Х2 + *з) = ^^1(^2*3) =

= X,((X2/\){X,/\)) = xJ((x2mx,/l)) = (xJiiX2mx,/m/l.

Все этапы этих преобразований показывают, что

х^/{х2/х,)*

*(xjx2)l(xjx^).

Т.е. свойство дистрибутивности несправедливо для

2 Автомат как основной элемент информационных систем

функции Шеффера от трех переменных, а следовательно, несправедливо и

для ««» переменных.

Необходимо указать на возможность возникновения следующего за-

блуждения: функция Шеффера равносильна функции отрицания конъюнк-

ции. Так как конъюнкция обладает всеми свойствами (коммутативностью,

ассоциативностью, дистрибутивностью), то по этой причине и функция

Шеффера должна была бы иметь эти же свойства. Однако равносильность

функций на всех наборах не обязательно совпадает с наличием одинаковых

свойств, что и подтверждает пример функций Шеффера и НЕ—И.

Функция Пирса (Вебба) (-1) — функция, которая описывается выраже-

нием А', i ^2 -

.V,

+ Х2

= Д:|Хз •

Для функций Пирса (Вебба) справедливы аксиомы;

xi х

х\

дг

О =

А;

= 0;

xix

f3;

xif3

x; i-J.| = 0,

что подтверждается таблицей 2.8.

I а б л

!! а 2-8

xix

.liO

.ai

Till

()

Элементарные булевы функции И, ИЛИ, НЕ выражаются через функ-

цию Пирса (Вебба) следующим образом:

i Х\

дг,дг2 =(Xi J.jr,)J.(Aj J-Xj); (2-9)

Х^+Х^ = (Х,

Д^2 )

•!-

(*1

J-

)•

Для функции Пирса (Вебба) справедливо свойство коммутативности

только для двух переменных: дг, i

дг,

= Xj

•

Функция Пирса (Вебба), так

же как и функция Шеффера, является двуместной функцией. Следова-

тельно, невозможны записи вида: х^ i

х-^

i ...i х^; для установления

приоритетов обязательно должны использоваться скобки, которые опре-

деляют последовательность осуществления операций:

(x^

ix2)ix,i(x,

ix^)).