Савельвев А.Я. Основы информатики

Подождите немного. Документ загружается.

! I 6

Времепи^Ле

булевы функции

памятью состоит в том, что алгоритм их работы зависит от времени. Следо-

вательно, в число переменных, от которых зависит выходная функция схе-

мы с памятью, должно входить время t. Но время не является двоичной пе-

ременной. Поэтому вводится понятие автоматного времени, принимающего

дискретные целочисленные значения О, I, 2 и т. д. Это означает, что работа

схемы с памятью распадается на ряд интервалов, в течение которых авто-

матное время условно принимает постоянное значение.

Временная булева функция (ВБФ) — логическая функция

V ^ф(Г|, .v,,..., V,,, ^), принимающая значение (О, ]] при 0<^<.v-1,гдe

,v — количество интервалов автоматного времени.

Можно утверждать, что число различных ВБФ равно 2' . В самом де-

ле,

если функция времени принимает s значений, т. е. г =

0,1,

2, ...,5 - 1, и

каждому интервалу времени соответствует 2" различных двоичных набо-

ров,

то всегда будет .v2" различных наборов. Следовательно, общее число

ВБФ равно 2'" -

Любая времещшя булева функция может быть представлена в виде

у - ф(Х|, Х^, •••»-У„,0-Фо'^0 "^ Ф|'^1 '^•••'^ Ф,-1'^(-| ,

(11.7)

[дс ф, — копьюик1нвныи или дизъюнктивный терм от переменных

(ЛрХ,,.-.,^,,); т^ — вспомогательная функция, принимающая значение

X, ={0.!} в момент времени г..

<1>орма представления временных логических функций (11.7) позволяет

применить к функциям у все методы упрощения и минимизации, рассмот-

ренные ранее.

Пример ! 1.8.11реобразов;пь функцию, прелсгавлеииуютаблицей ! !.7, в вил (1 !.7).

Таблица 11.7

()

.«,

(

Wl.'l-')

'^1

<p(i|. д:;,))

!'С m е И

е Функцию v ^ ф(Л|, х-,,1) представляем совокупностью трех логических

ф\икиин <pjj( \|. х-,) - Я'А^г

'^2)

•

*?i(-^]-

^2) • которые

ДЛЯ

1аблиць! 11.7 имеют вид

277

/ / Логическое описание и анализ электронных

На (1Снова1Ши (117) записываем окопчагсльпый вид временной логической ф>икиии

у = X^XJTQ V{J|.V2 V

Х\Х^)Х^

vtjTj,

с i.8)

Ответ: см. формулу (! 1.8)-

Разложение (11.7) можно применить только к периодическим времен-

ным функциям. Переход к схеме от логического выражения вида (П.7)

можно осуществить следующим образом.

Предположим, что на выходах некоторой схемь! (деи1и<|)раторй) в мо-

менты времени i появляются сигналы:

если ^1 = О, то на выходе

сигнал т^, = 1, при Х| - О, Xj -

;

если Ь ~ Ь то на выходе 2 сигнал т, = 1, при Тд =

, Xj - О;

если

t•^

= 2, то на выходе 3 сигнал ij = I, при t„ =

, т, -0.

Для каждой функции (р, строим соответствуюи^ую логическую схему,

не зависящую от переменной t. После этого все схемы соединяем между

собой в соответствии с (М .7).

Рекуррентная булева функция (РБФ) — логическая функция, завися-

щая как от текущих значений .т, входных переменных, так и от нредшесг-

вуюших значений самой функции

у^,_ц-

Полная аналитическая запись та-

кой функции

У, =^(0,

при

>0,

где х, —- текущие значения входных переменных; з', — значения выход-

ных функций в момент времени j -t -\; 1-2 и т. д.

Чтобы гфедставить иеобходимос1ь рекуррентных булевых ||)ункпнй,

рассмотрим некоторый физический элемент, работа которого оппсишается

соответствием;

/..,0 1 2-.J, I I,

д..-

Vji Л| г,... г, , х,

V, =/(v./)..-0 -Хо

-'^i----^,

2 Ч !

Следовательно,

у^_^^

=х,. Отсюда значение выходною cni пала в мо-

мент времени t

равно значению входного сигнала в момент времени /.

Такой элемент называют задержкой: D{t)

-—

его логический опера iop.

Рассмотрим логическую схему, имеющую цепь обратной связи с вклю-

ченной в нее схемой задержки (рис. 11.I7, а). Предположим, что в качес1ве

278

117 Иоследовательноспшый автомат

схемы с функцией /(х, у) взята логическая схема ИЛИ. Тогда в совокуп-

ности эта схема работает так, как показано на временной диаграмме

{рис.

11.17, б), т. е. /(х, у) = х,^| V >>,,

т)

>'*

""^ЬгЬтг

Рис.

11.17. Схема с обрат

мой

связью

В схеме рис. 11.17 выходной сигнал зависит как от входного сигнала в

д:1И11Ь!й момен! времени, 1ак и от выходного сигнала в предшествующий

момент времени, В самом общем случае при наличии и входов и к цепей об-

ратной связи, в которых осуществляется равная задержка, такие схемы могут

быть описаны с помощью рекуррентных временных логических функций.

Следовательно, любая рекуррентная булева функция может быть

реалтована с помощью набора логических операторов функциональных

элементов, иредставчяющнх обычные функции алгебры логики, и операто-

ров i:\eM Ш()ержки.

ИЛ. Последовательностный автомат

Рассмотрим частный случай рекуррентной временной логической

ф\нкции, так называемой вырож-дениои. Это соответствует случаю, когда

на вход функциональной схемы не подаются входные переменные, а посту-

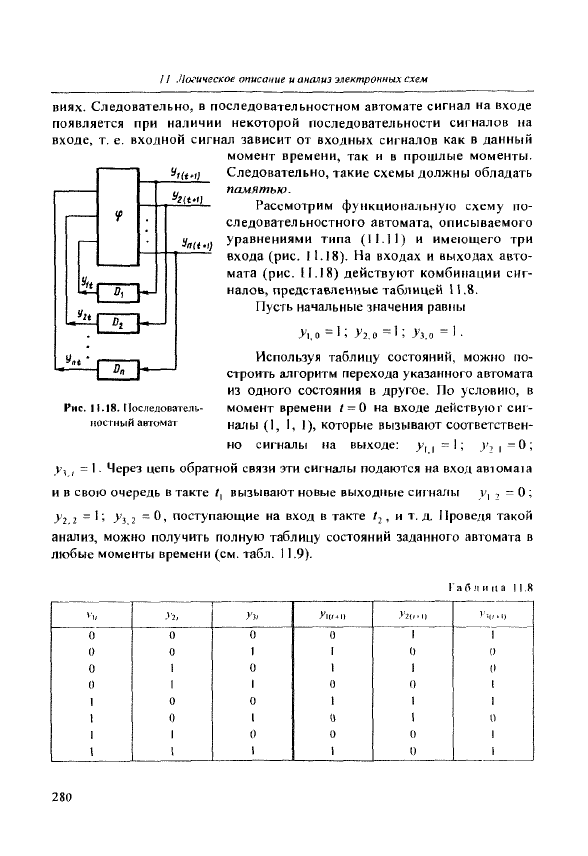
uaioi юлько сигналы по цепям обратных связей (рис. 11.18). /|ля таких

случаев рекуррентные функции имеют вид

»'ими ='ff>,(.Vi,.>'n,-it----Vi(,-,)---'y«/M •-•'>'«,('-»)• (11.10)

Для ф>икцпй (il.lO) должны быть заданы начальные условия при

/-().

Предположим, что обратная связь осуществляется с задержкой на

I такг. Го1дп уравнения (I 1.10) примут вид

Иоследовательностные автоматы — это функциональные схемы,

описываемые уравнениями типа (11.I I), при заданных начальных усло-

279

/ / Логическое описание и анализ электронных схем

ВИЯХ. Следовательно, в последовательностном автомате сигнал на входе

появляется при наличии некоторой последовательности сигналов па

входе, т. е. входной сигнал зависит от входных сигналов как в данный

момент времени, так и в прошлые моменты.

Следовательно, такие схемы должны обладать

памятью.

Рассмотрим функциональную схему по-

следовательностного автомата, описываемого

уравнениями типа {11.11) и имеющего три

входа (рис. 11.18). На входах и выходах авто-

мата {рис. 11.18) действуют комбинации сиг-

налов, представленные таблицей П .8.

Пусть начальные значения равны

1=1;

Рис.

11.18. Последователь-

постный автомат

Л.о ^ f • До =i;

У2.(

Используя таблицу состояний, можно по-

строить алгоритм перехода указанного автомата

из одного состояния в другое. По условию, в

момент времени

= 0 на входе действуют сиг-

налы (1, 1, I), которые вызывают соответствен-

но сигналы на выходе: у^

=\-^ ^^ i ^

;

Vi , =

1 -

Через цепь обратной связи эти сигналы подаются на вход автомата

и в свою очередь в такте г, вызь!вают новые выходные cm налы y^ ^ =

;

У2 2 =^у >'з 3 ~ *^' поступающие на вход в такте г^, и т. д. Проведя такой

анализ, можгю получить полную таблицу состояний заданного автомата в

любые моменты времени (см. табл. 11.9).

1'аб

л II

на N8

^'и

V-;,

УУ

ЛС!)

.>'2(..1|

1'1(мИ

()

280

Последовательно!

ыи автомат

Если поменять начальные условия, то таблица состояний автомата из-

менится. Читателю предлагается самому убедиться

этом, приняв у^

=\;

у^

=]-^

у^ ^ =0.

Надо помнить, что алгоритм функционирования автома-

та задается таблицей 11.8. Состояния автомата

процессе его функциони-

рования могут повторяться

определенным периодом (для таблицы 11.9

он

равен 6).

Таблица

П.9

.V,,

Уи

у 1.1

ЛО»!)

Л(..|)

Л(-.|)

Имея таблицу состояний автомата, можно получить логическое описа-

ние устройства,

помощью которого можно реализовать этот автомат.

11о таблице 11.8 запишем СНДФ для всех выходных переменных:

{У10>1)=У1,У2,УУ '•^УиУ2,У11 •^У!,У2,Уз, '^УчУьУзГ,

\У21,*1) =УиУ2,У>, '^УиУ2,Уг,

УиУ2,Уц'^ УиУ2,У},'

[>'м<.|) =УиУ2,У2., '^УиУ2,Уг, "^УиУг/Уу, ^УьУг.Уг, '^УчУ2,Уу,-

Используя методы минимизации, получим после преобразований сле-

дующие формулы:

\Уч,,,) ={УиУ2, ^У|,.ь,)Л, '^(УьУ2, ^УьУнЖ',

\У1ы\)=УмУ^:'^УиУ2,;

\Ум,.\)

=УьУ1, '^

У2,УУ

^У21УЪ,-

(11.12)

11а осповапии логических формул можно построить функциональную

схему логического автомата.

281

// Логическое описание и анализ

-улектрпиных

схем

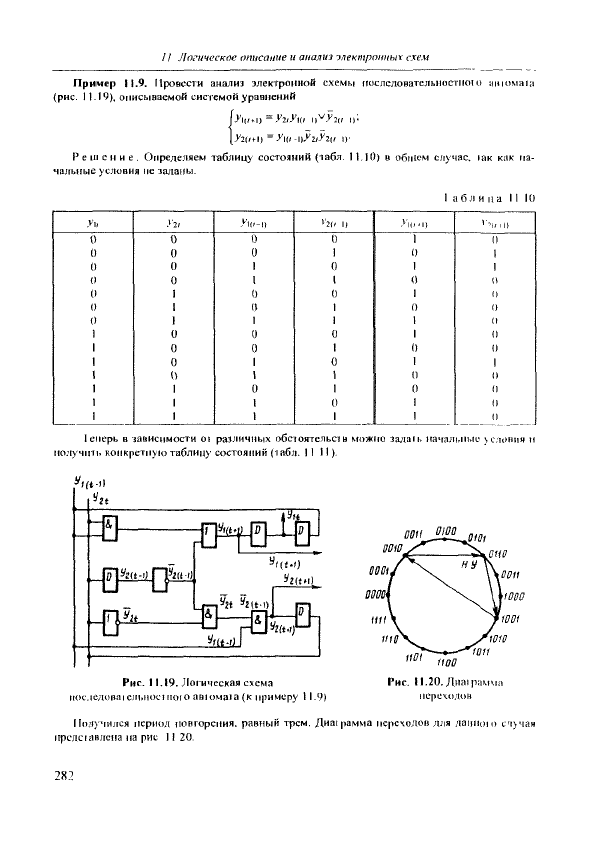
Пример И.9. Провести анализ электронной схемы 1Госле;ювателы!остно1 о iinioMaia

(рис.

11.19), описываемой системой уравнений

У2и^ц=У\(>-\)У2>Уги

I,-

Решение, Определяем таблицу состояний (табл. 11.10) в общем случае. 1ак как на-

чальные условия не заданы.

i абли на II 10

>'|.

(}

Ун

>11--1)

^'гl/

>'i(IM|

'•.„,„

leiiepb в зависимости oi различных обсгоятельсчв можно задан, начальные \с.'к>»пя н

по.чучни. конкретную таблицу состояний (табл. 11 11)-

е-

№tfb%^

'(((•I)

Aitji

4llt.,f-

Рис. 11.!9. Логическая схема

иос.|едова|ел1.иосп1010 ав!ома1а(к примеру 11.9)

Рис.

1.20. Дна! рамм

персчолов

Получился |гериол повторения, равный трем. Диаграмма переходов лля данН()И)

1:'1>чая

прелс1авлена на рис 11 20.

282

I! 8 Анализ последоватвльностных автоматов

Таблица li.l!

v„

{)

Ун

Уч,^»

Л(,-|,

}

^(,.1)

Л|„|)

Отает япали! ргрелставнеи п габлицах 11.10 и !!,!!.

11.8.

Анализ иоследователыюстных автоматов

с помощью рекуррентных булевых функций

/1ля liejien анализа введем понятие обобщенног-о последовательностно-

I о aBioMaia, схема которого представлена иа рис.

11.21.

Такой автомат опи-

сываечся следующей системой уравнений:

чн,,1> ='Pi(-fi(/.i).---.-^«(-ti);?i/'••-.?«;?!«-») •••?.(«-»));

'/,(,.1)

='p,(-f

к,.i).-----f„('.i);?i,.

•••.'/«;

?!('-*)

•••?.(<-*));

{11.13)

^.(,.1) '4',{.fi(,tii.---..f„(-.i);'/i,,•••.?„;?!(,-») •••?.(,-»)X

'ЛЬ'

f,(,,i) — входные переменные в момент (' + !); q,, — внутреннее со-

С10ЯПИС схемы в момент времени f;

(/,,,+1)

— внутреннее состояние в мо-

меш {I fl);Z(,,|, —выходные переменные в момент времени {( +1).

IpcflnojrojKHM, что некоторая схема описывается таблицей состояний

(1абл.

11.12),

В соответствии с основной теоремой выходная функция д,^, записыва-

йся в виде уравнения

283

// Логическое описание и анализ электронных схем

которое после преобразований и минимизации определяется следующим

образом:

?,*1 =^2(«1)'?, VX||,^|,?, . (11.14)

Схемы,

функционирование которых описывается уравнениями типа

1.14),

назовем триггерными схемами. Они обладают двумя устойчивыми

внутренними состояниями (д, не/,), выходной сигнал в таких схемах зави-

сит как от входного сигнала, так и от внутреннего состояния.

Таблица 11.!2

^|(/.|)

^Цп\)

я,

?,.!

ч,„

Таким образом, триггерные схемы являются частным случаем обоб-

щенного последовательностного автомата.

Для системы уравнений (1113) введем сле-

•'('•'J дующие условные обозначения:

"((О!)

»'(t-l.

i's,...,

ffb

•Ии%

«Р~-

LiT

Q, =(?i,.?2,-•••.?«};

Тогда уравнения (11.13) приобретаю i вид:

г,„=Ф(х„|,й)

и назьрваются каноническими уравнениями авю-

мата.

Эти уравнения подтверждают, что в любом

последовательиостном автомате внутреннее со-

стояние автомата в момент времени (? + 1) зависит ог внутренне!о сосгоя-

ния в момент t и от входных сигншюв в момент (/ + I). Выходной сигнал

I'lic.

11.2!. Обобтеппый

логический автомат

11.9. Разновидности триггерных схем

автомата в момент (? + I) зависит также от внутреннего состояния автомата

в предшествующий момент и от состояния входов в момент (/ + I).

Рассмотрим следующую важную теорему.

Любую логическую схему с памятью можно представить в виде

совокупности логических схем И, ИЛИ, НЕ и триггерной схемы.

В самом деле, опираясь на следствие 1 из теоремы о разложении

функции по к переменным, любое уравнение из системы (11.13) мож-

но преобразовать следующим образом:

OcyuiecTBHB замену, получим

Ч10 RBJifleicfl уравнением триггерной схемы с двумя входами, причем

функции Мц,.^|, и «2(;+1) ЯВЛЯЮТСЯ ВХОДНЫМИ функциями триггсрй.

проведя подобное преобразование всех уравнений в системе (11.I3),

приходим к выводу, что теорема справедлива.

[Ipiiiviep И,10. Уравнение Уц,*]) "-'^n'+o^i'^-'^20*1) преобразовать так, чтобы его можно

было

реалмзова!

с помощью триггера и других логических функций.

Решение. Гак как триггер описывается уравнением у^ =

Х;

l^.\Уl

^ ^\

1*\У,.

тО' введя

обозначения Xj ,^\ =

y\i,\'

^i /*i =

У\.и,\

•,

У1

I^\ ~

У\

/ц "Р" >'/='. в результате подстановки

V,, "

п vicxoiiHoe уравнение получим у1 ,^| = л, ,^| v-Xj „, .

Однако у^,,1

'-=

у,^, при у, =

, Значит, подставив у, =0 в исходное уравнение, полу-

чим >', ,,| -

V-,

,,|

Отвепг y^ ,^| = (г, r,i ^ Xj ,.ц)>', v

.х^

^^у, -

И.9.

Разновидности триггерных схем

Л.

Трнпериые схемы с раздельной установкой входов {RS-

трнггеры) (рис. 11.22).

Это наиболее распространенная и простая схема, которая может быть

реализована с помощью различных элементов И—НЕ, ИЛИ—НЕ. Схема

285

/ / Логическое описание и анализ электронных схем

имеет два входа S и R vi два выхода Q а Q' • Работа такой схемы огшсывает-

ся следующими уравнениями:

Применив теорему де-Моргана, указанные уравнения можно преобра-

зовать:

e = Sve';y = /?vy.

Рассмотрим следующие наиболее характерные ситуации, когорые мо-

гут возникнуть при работе Дб'-триггера.

S - R = 0 (активных сигналов на входе нет).

Это нормальное состояние схемы и уравнения функционирования

триггера показывают, что Q = Q'. В самом деле, если У = 1, то У =

, или

если у-О, то Q' = ]. Значит, есть два устойчивых состояния, в одном из

которых система остается до прихода очередного входного сигнала. Однако

уравнения этого не регистрируют.

S =

Д = О.

Из уравнения следует, что y = lvy' = l и

Q'-OvQ'

= 0. Следова-

тельно, при таких входных условиях выход принимает значение 1.

акое

состояние схемы назовем единичным.

3. 5 = 0, Д =

Это состояние противоположно состоянию 2. Назовем это состояние

ну.чевым.

5 = Д =

Рис. 11.22. Схема /?5-триггера

Возникла самая трудная ситуация, так как получается Q = Q' = i ,

Невозможность такого состояния обусловливает нестабильность рабо-

286