Сараев П.В. Нейросетевые методы искусственного интеллекта

Подождите немного. Документ загружается.

Если матрица G(w

) аппроксимируется на каждом шаге диагональной

матрицей µ

I, µ

 0, получается метод Левенберга-Марквардта

∆w

= −



T



)+µ



T

)R(w

). (2.21)

При этом шаг спуска вдоль найденного направления всегда является единич-

ным, а параметр µ

выбирается так, чтобы минимизировать целевую функ-

цию. В отличие от других метод Левенберга-Марквардта не попадает под

рассматриваемую схему оптимизации; он относится к классу методов дове-

рительной окрестности. При µ

→ 0 направление почти совпадает с направле-

нием метода Гаусса-Ньютона, при µ →∞— с направлением антиградиента.

В задачах с большим значением целевой функции (с большой невязкой)

целесообразно использовать квазиньютоновские приближения H

матрицы

G(w

). Если используется формула BFGS для нахождения приближения, то

получается следующее:

t+1

= H

−

где M

= R

T



+ H

, s

= w

− w

t−1

и g

= R

T

J(w

) − R

T

t−1

J(w

t−1

).Нана-

чальной итерации берется H =0. Периодически для уменьшения влияния

погрешностей округлений снова полагают H =0. Если приближение осу-

ществляется на основе DFP-метода, то

t+1

= H

(g

− H

) g

+ g

(g

− H

)

−

(g

− H

)





где g

= R

T

J(w

)−R

T

t−1

J(w

). Следует отметить, что специальные методы ре-

шения НЗНК не всегда работают лучше методов оптимизации произвольных

дифференцируемых функций.

Расчет производных выходов сети по весам НС ПР возможен с помо-

щью процедуры, учитывающей суперпозиционный характер структуры сети

аналогично методу ОРО. При этом процедура построения матрицы Якоби да-

же несколько упрощается ∇

y(w

) в связи с тем, что подлежит вычислению

производная не функционала, а выхода сети.

2.3.4. Обучение на основе декомпозиции вектора весов с исполь-

зованием псевдообращения

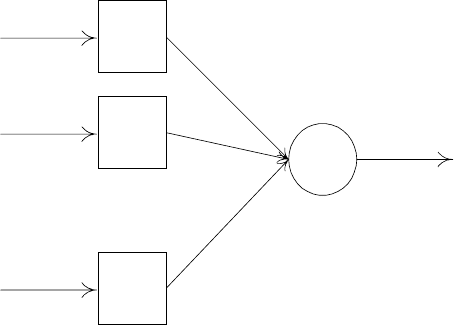
Простейшей НС ПР является НС, не содержащая скрытых слоев, с

единичной функции активации (рис. 2.6). Функция y =



i=1

, реализуемая

данной сетью, представляет собой линейную по весам функцию.

Рис. 2.6. Простейшая нейронная сеть

Ее обучение может быть произведено за один шаг и аналитически пред-

ставлено в виде

w =



y, (2.22)

где



X ∈ R

k×n

— матрица, составленная из входов обучающего множества:



X =







x

... x

x

... x

... ... ... ...

x

... x







Формула (2.22) является псевдорешением уравнения



Xw = y.

Перейдя к рассмотрению стандартной НС ПР, заметим, что ее функ-

ционирование можно представить формулой

y =Ψ(v)u,

где Ψ(v) — матрица выходов нейронов скрытого слоя, зависящая от векто-

ра нелинейно входящих весов v (веса матрицы W

(1)

); u — вектор линейно

входящих весов, состоящий из весов нейрона выходного слоя (W

(2)

). Таким

образом, вектор весов w разбит на два подвектора — v и u.

Для фиксированного вектора v аналогично (2.22) следует справедли-

вость формулы

u =Ψ(v)

y. (2.23)

Формулу (2.23) будем называть базовым линейно-нелинейным соотношением

(БЛНС), связывающим линейно и нелинейно входящие в НС веса. Она поз-

воляет находить оптимальный вектор u при заданном v,однако,как(2.22),

полностью решить задачу обучения НС ПР не в состоянии. Для вектора v

формулы, аналогичной (2.22), нет, т.к. неизвестно, какие значения должны

выдавать нейроны скрытого слоя.

Можно записать, что НС ПР реализует функцию

y(u, v; x)=



j=1

(v, x), (2.24)

где ψ

(v, x) —выходj-го нейрона скрытого слоя при входном векторе сети

x. Здесь u ∈ R

, v ∈ R

, p + q — суммарное количество весов НС. Функцио-

нал (1.8) можно переписать в следующем виде:

J(u, v)=



i=1



j=1

(y(u, v; x

) − y

)



i=1



j=1

(v, x

) − y

)

. (2.25)

Функция (2.24) может быть представлена в векторно-матричной форме

y(u, v; x)=ψ(v, x)

u, (2.26)

где ψ(v, x)=



(v, x) ψ

(v, x) ... ψ

(v, x)



∈ R

. На обучающем множе-

стве рассматриваемая функция ψ(v, x) образует матрицу Ψ(v) ∈ R

k×q

Ψ=







(v, x

) ψ

(v, x

) ... ψ

(v, x

)

(v, x

) ψ

(v, x

) ... ψ

(v, x

)

... ... ... ...

(v, x

) ψ

(v, x

) ... ψ

(v, x

)







Для НС ПР матрица Ψ(v) состоит из выходов нейронов скрытого слоя на

обучающем множестве.

С учетом этого задача оптимизации функционала (1.8) (или, что то же

самое, (2.25)) может быть записана как

J(u, v)=

Ψ(v)u − y

→ min . (2.27)

Из БЛНС (2.23) следует, что НЗНК (2.27) эквивалентна задаче



J(v)=Ψ(v)Ψ(v)

y − y

→ min . (2.28)

Преимущество минимизации функционала в задаче (2.28) состоит в том, что

оптимизация производится лишь по нелинейно входящим параметрам v

, ли-

нейные определяются на основе соотношения (2.23). Недостатком является

то, что снижение размерности задачи приводит к необходимости оптимизации

более сложной функции. Данная задача впервые была поставлена Голубом

(Golub) и Перейрой (Pereyra) в 1973 г.

Для вывода метода обучения НС на основе декомпозиции вектора весов

с псевдообращением введем обозначение

H(v)=Ψ(v)Ψ(v)

y − y =(Ψ(v)Ψ(v)

− I

)y, (2.29)

где I

— единичная матрица порядка k. Основной задачей является определе-

ние матрицы Якоби H



(v) по вектору нелинейно входящих весов v. На основе

матрицы H



(v) можно реализовывать алгоритмы обучения НС, базирующи-

еся на методах решения НЗНК. Соотношение

∇



J(v)=H



(v)

H(v) (2.30)

позволяет использовать другие алгоритмы оптимизации, использующие ин-

формацию о градиенте минимизируемой функции ∇



J(v) по вектору v.

Производная матрицы A(B) ∈ R

m×n

по матрице B ∈ R

k×p

определяется

следующим образом (для упрощения записи аргумент в дальнейшем будем

опускать):



∂A

∂B







∂A

∂b

∂A

∂b

...

∂A

∂b

∂A

∂b

∂A

∂b

...

∂A

∂b

∂A

∂b

∂A

∂b

...

∂A

∂b







∈ R

mk×np

Матрицу Якоби A



= A



по вектору v ∈ R

будем рассчитывать как

производную матрицы по вектор-строке v



∂A

∂v



∂A

∂v

∂A

∂v

...

∂A

∂v



∈ R

m×np

. (2.31)

Такой способ вычисления связан с определением матрицы Якоби как матри-

цы, составленной из транспонированных градиентов.

В общем случае для производной произведения AB двух матриц A ∈

m×n

и C ∈ R

n×l

по третьей C ∈ R

k×p

, справедлива следующая формула:

(AC)



∂(AC)

∂B

∂A

∂B

⊗ C)+(I

⊗ A)

∂C

∂B

= A



⊗ C)+(I

⊗ A)C



где ⊗ — символ тензорного (кронекеровского) произведения матриц. Тензор-

ное произведение определяется как блочная матрица следующего вида:

A ⊗ B =







B ... a







∈ R

mk×np

Если дифференцирование ведется по вектор-строке v

∈ R

1×p

, то производ-

ная произведения матриц вычисляется как

(AC)



∂(AC)

∂v

∂A

∂v

⊗ C)+

∂C

∂v

= A



⊗ C)+C



. (2.32)

Пример 2.2.

Проверим справедливость формулы (2.32). Пусть даны зависящие от v =





векторы a =



(v) a

(v)



и c =



(v)



. Прямое вычисление (ac)



∂(ac)

∂v

дает следующий вектор:

(ac)



=(a

+ a

)





+ a

)



+ a

)









+ a



+ a



+ a



+ a



+ a



+ a





а применение формулы (2.32) приводит к

(ac)















0 c





















+ a



+ a









+ a



+ a









+ a



+ a



+ a



+ a



+ a



+ a





Оба способа дают идентичный результат. 

Для разработки метода обучения найдем способ вычисления производ-

ной псевдообратной матрицы (A

(v))



, состоящей из элементов-функций. По-

лучение в общем случае аналитической формулы для вычисления требуемой

производной невозможно (прямой способ). Имеется возможность вычисления

(v))



косвенным способом. Вывод формулы для вычисления производной

псевдообратной матрицы осуществляется в четыре этапа:

1. Нахождение производной обратной матрицы.

2. Определение производной в случае, когда дана прямоугольная матрица

полного столбцового ранга.

3. Получение аналогичной формулы для прямоугольной матрицы полного

строкового ранга.

4. Получение искомой формулы на основе скелетного разложения матри-

цы.

Этап 1.

Для квадратной невырожденной матрицы A с учетом (2.32) имеем



−1





= A





⊗ A

−1



+ A



−1





= I



=0,

откуда следует



−1





= −A

−1





⊗ A

−1



. (2.33)

Этап 2.

Пусть B — матрица полного столбцового ранга. В этом случае ее псевдооб-

ратная выражается как





−1

. (2.34)

Применение формулы (2.32) дает









−1







⊗ B







−1







Матрица B

B — квадратная невырожденная, применение к ней (2.33), при-

водит к формуле







= −(B

−1



⊗ (B

−1

)(I

⊗ B





−1







= −(B

−1

)



⊗ B)(I

⊗ (B

−1

)(I

⊗ B

)−

− (B

−1



⊗ (B

−1

)(I

⊗ B

)+(B

−1

)



Обычное и тензорное произведение связаны следующим образом:

(A ⊗ B)(C ⊗ D)=(AC) ⊗ (BD),

если матрицы имеют согласованные размеры. Из этой формулы получаем

важное для нас следствие

⊗ B)(I

⊗ D)=(I

) ⊗ (BD)=I

⊗ (BD), (2.35)

и поэтому







= −(B

−1

)



⊗ B(B

−1

)−

− (B

−1



⊗ (B

−1

)+(B

−1

)



На основе (2.34) и равенства (B

−1

=(B

= B

получается







= −B

)



⊗ BB

) − B



⊗ B

)+B

)



Группируя первое слагаемое с третьим и считая, что матрица B состоит из

k строк, приходим к формуле







= B

)



− (I

⊗ BB

)) − B



⊗ B

Операция тензорного произведения дистрибутивна относительно сложения

матриц, а I

= I

⊗ I

, поэтому:

− (I

⊗ BB

)=I

⊗ I

− (I

⊗ BB

)=I

⊗ (I

− BB

на основании чего приходим к окончательной формуле для производной псев-

дообратной матрицы полного столбцового ранга







= B

)



⊗ (I

− BB

)) − B



⊗ B

). (2.36)

Этап 3.

Рассмотрим случай с матрицей полного строкового ранга C. Псевдообратная

такой матрицы выражается так:

= C





−1

Вывод формулы для расчета (C

)



аналогичен выводу (2.36):







=(C

)





⊗ (CC

)

−1



+ C



(CC

)

−1





=(C

)





⊗ (CC

)

−1



− C

(CC

)

−1

(CC

)





⊗ (CC

)

−1



=(C

)





⊗ C



− C





⊗ C



− C









⊗ C



откуда получается формула









− C



)





⊗ C



− C





⊗ C



. (2.37)

Здесь q — число столбцов в матрице C,а(C

)



=(C



)

. Формулы (2.36)

и (2.37) обладают определенной симметрией.

Этап 4.

Рассмотрим матрицу A ∈ R

k×q

произвольного ранга r  min{k, q}. В этом

случае существуют матрица полного столбцового ранга B ∈ R

k×r

и матрица

полного строкового ранга C ∈ R

r×q

такие, что A = BC. Такое разложение

матрицы называется скелетным. При этом справедливо равенство

= C

. (2.38)

Учитывая формулы (2.32), (2.36), (2.37), (2.35), а также некоторые другие

свойства псевдообратных матриц, получаем формулу для вычисления произ-

водной псевдообратной матрицы произвольного ранга:







=(I

− A

A)(A

)



⊗ A

+ A

)



⊗ (I

− AA

)) − A



⊗ A

). (2.39)

Здесь A



∈ R

k×qp

и (A

)



∈ R

q×kp

. Из анализа размерностей матриц видно,

что действительно, (A

)



∈ R

q×kp

Вернемся к нахождению формулы для вычисления H



(v).Дляэтого

необходимо знать производную не самой матрицы Ψ, а производную произ-

ведения ΨΨ



ΨΨ





=Ψ



⊗ Ψ

)+Ψ(Ψ

)



=Ψ



⊗ Ψ

)+Ψ(I

− Ψ

Ψ)(Ψ

)



⊗ Ψ

+ΨΨ

(Ψ

)



⊗ (I

− ΨΨ

)) − ΨΨ



⊗ Ψ

Принимая во внимание, что

ΨΨ

=(ΨΨ

)

=(Ψ

ΨΨ

)

=Ψ

аслагаемое

Ψ(I

− Ψ

Ψ) = Ψ − ΨΨ

Ψ=0,

получаем формулу



ΨΨ





=Ψ

(Ψ

)



⊗ (I

− ΨΨ

)) + (I

− ΨΨ

)Ψ



⊗ Ψ

). (2.40)

Размеры матриц согласованы, (ΨΨ

)



∈ R

k×kp

Формула (2.40) позволяет найти производную (точнее, матрицу Якоби)

H(v), определенную по (2.29), по вектору нелинейно входящих весов v:



=(ΨΨ

)



⊗ y)=

=Ψ

(Ψ

)



⊗ (I

− ΨΨ

)y)+(I

− ΨΨ

)Ψ



⊗ Ψ

y) ∈ R

k×p

. (2.41)

Метод обучения НС ПР на основе декомпозиции вектора весов с псев-

дообращением может быть применен и к многослойным сетям. Функциони-

рование m-слойной НС ПР можно представить в виде

y = y(u, v, x)=



i=1

m−1

(v, x),

где y

m−1

(v, x) —выходi-го нейрона последнего скрытого, (m − 1)-го, слоя.

Рассмотренный выше метод обучения одновыходных стандартных НС ПР

практически без изменений применяется к многослойным сетям. Изменения

касаются только процесса нахождения матрицы Якоби для Ψ(v) (и, соответ-

ственно, Ψ

(v)) по вектору весов v. Для этого применяется способ, анало-

гичный процедуре ОРО и связанный с учетом суперпозиционного характе-

ра НС ПР. Требующая вычисления производная

∂y

(m−1,l

)

∂w

(h,i)

, l =1,...,N

m−1

h =1,...,m− 2, i =1,...,N

, определяется как

∂y

(m−1,l)

∂w

(h,i)

∂y

(m−1,l)

∂y

(h,i)

∂y

(h,i)

∂net

(h,i)

∂net

(h,i)

∂w

(h,i)

(l,h,i)

∂y

(m−1,i)

∂y

(h,i)

h+1



d=1

∂y

(m−1,l)

∂y

(h+1,d)

∂y

(h+1,d)

∂y

(h,i)

h+1



d=1

(l,h+1,d)

∂y

(h+1,d)

∂y

(h,i)

Начальное условие получается следующим образом:

(l,m−1,i)

∂y

(m−1,l)

∂y

(m−1,i)



1,i= j

0,i= j

2.3.5. Глобальное обучение нейронных сетей

Рассмотренные выше методы оптимизации носят локальный характер,

т.е. позволяют оптимизировать функцию не на всей области определения, а