Рогов А.А, Семенова Е.Е, Чернецкий В.И, Щеголева Л.В - Уравнения математической физики. Сборник примеров и упражнений

Подождите немного. Документ загружается.

30 Глава I. Основы операционного исчисления

2) x

− x

− 6x = 4, x(0) = 1, x

(0) = 0;

3) x

+ 2x

− 3x = e

−t

, x(0) = 0, x

(0) = 1;

4) x

+ 2x

= t sin t, x(0) = x

(0) = 0;

5) x

000

+ 3x

− 4x = 0, x(0) = x

(0) = 0, x

(0) = 2;

6) x

000

+ x

= sin t, x(0) = x

(0) = 1, x

(0) = 0;

7) x

000

+ 6x

+ 11x

+ 6x = 1 + t + t

, x(0) = x

(0) = x

(0) = 0;

8) x

− x

= −2t, x(2) = 8, x

(2) = 6;

9) x

+ 2x

+ x = 2 ·e

1−t

, x(1) = x

(1) = −1;

10) x

+ 2x

+ x = sin t, x(0) = x

(0) = x

000

(0) = 0.

13. Найдите решения систем уравнений, удовлетворяющие заданным

условиям:

(

+ y = 0,

+ x = 0,

x(0) = 1, y(0) = −1;

(

+ 7x − y = 0,

+ 2x + 5y = 0,

x(0) = y(0) = 1;

(

− y

− 2x + 2y = 1 − 2t,

+ 2y

+ x = 0,

x(0) = y(0) = x

(0) = 0;

(

− 3x

+ 2x + y

− y = 0,

−x

+ x + y

− 5y

+ 4y = 0,

x(0) = x

(0) = y

(0) = 0,

y(0) = 1;

(

− x

+ 9x − y

− y

− 3y = 0,

+ x

+ 7x − y

+ y

− 5y = 0,

x(0) = x

(0) = 1,

y(0) = y

(0) = 0;

(

+ y

− y = e

+ y

+ 2y = cos t,

x(0) = y(0) = 0;











= −x + y + z + e

= x − y + z + e

= x + y + z + 4,

x(0) = y(0) = z(0) = 0;

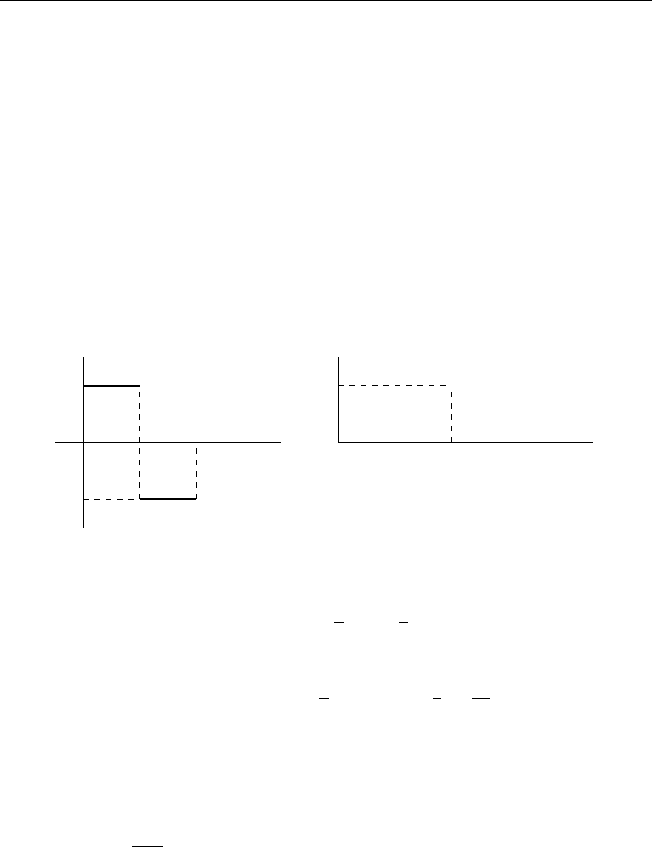
§ 3. Применение преобразования Лапласа 31











= y + z,

= 3x + z,

= 3x + y,

x(0) = 0, y(0) = z(0) = 1;











= 3(y − x + z),

= x − y,

= −z,

x(0) = x

(0) = 0,

y(0) = 0, y

(0) = −1,

z(0) = 1, z

(0) = 0.

14. Решите задачи Коши в случае, когда функция f(t) в уравнении за-

дана графически:

1) x

+ x = f(t), 2) x

+ 9x = f(t),

x(0) = x

(0) = 0, x(0) = 0, x

(0) = 1

f(t)

−1

0 1 2

¡@

f(t)

0 1 2 3

15. Решите следующие краевые задачи:

1) x

(t) + x

(t) = 2t, x(1) = 0, x

(1) = −1;

2) x

+ x = 2 sin t, x(0) = 1, x(

) = −

;

3) x

(t) − x

(t) = t ·e

, x(0) = 1, x(2) = e

;

4) x

+ x = t ·cos t, x(π) = −

, x(π/2) =

− 1

2. Дифференциальные уравнения с переменными коэффициентами. Рас-

смотрим уравнение вида

(t)x

(n)

(t) + a

(t)x

(n−1)

(t) + . . . + a

(t)x(t) = f(t), (3.3)

где a

(t), i = 0, n – многочлены степени m

, а функция f (t) является

оригиналом. Обозначим m = max{m

, m

, . . . , m

}. Будем предпола-

гать, что задача Коши для уравнения (3.3) с условиями

x(0) = x

, x

(0) = x

, . . . , x

(n−1)

(0) = x

n−1

(3.4)

32 Глава I. Основы операционного исчисления

имеет решение на множестве оригиналов. Пусть x(t)

↔

X(p). По теореме

о дифференцировании изображения имеем

(s)

(t)

↔

(−1)

L{x

(s)

(t)}

= (−1)

X(p) − p

s−1

− . . . − x

s−1

Таким образом, применяя к обеим частям уравнения (3.3) преобразова-

ние Лапласа, уравнение (3.3) преобразуем в дифференциальное уравне-

ние m–го порядка относительно изображения X(p). После этого задача

интегрирования уравнения (3.3) упрощается.

Пример 8. Найти решение уравнения:

(t) − (1 + t)x

(t) + 2(1 − t)x(t) = 0.

Решение.. Пусть x(t)

↔

X(p). Тогда, используя свойства дифференци-

рования оригинала и дифференцирования изображения, запишем:

(t)

↔

pX(p) − x(0),

(t)

↔

X(p) − px(0) − x

(0),

tx(t)

↔

−

dX(p)

(t)

↔

−

{pX(p) − x(0)} = −p

− X(p),

(t)

↔

−

X(p) − px(0) −x

(0)

= −p

− 2pX(p) + x(0).

Применив к заданному уравнению преобразование Лапласа, получим

следующее операторное уравнение:

− p

dX(p)

− 2pX( p) + x(0)−

−pX(p) + x(0) + p

dX(p)

+ X(p ) + 2X(p) + 2

dX(p)

= 0,

которое легко привести к виду:

− p − 2)

+ 3(p − 1)X(p) = 2x(0).

Решив полученное обыкновенное дифференциальное уравнение, напри-

мер, методом вариации произвольной постоянной, построим его общее

решение:

X(p) =

x(0)

p − 2

(p − 2)(p + 1)

§ 3. Применение преобразования Лапласа 33

Здесь c – произвольная постоянная. Далее, так как

p − 2

↔

(p + 1)

↔

t · e

−t

(p − 2)(p + 1)

↔

τe

−τ

· e

2(t−τ)

dτ =

− (3t + 1)e

−t

то общее решение заданного уравнения будет иметь вид:

x(t) = x(0)e

+ c

−

(3t + 1)e

−t

= (x(0) + c

− c

(3t + 1)e

−t

где c

– произвольная постоянная. /

Упражнения

16. Найдите решения уравнений:

1) t · x

− 2x

= 0; 2) t · x

+ (2t − 1) · x

+ (t − 1) · x = 0;

3) t · x

+ 2x

= 0; 4) x

+ (t + 1) · x

+ t · x = 0,

x(0) = 1, x

(0) = −1;

5) x

+ (t + b) · x

= 0, 6) x

+ t · x

− (t + 1) · x = 0,

x(0) = −1, x

(0) = 0, x(0) = x

(0) = 1.

b ∈ R;

17. Решите систему уравнений:











3tx

= 2x + y − z,

2ty

= x + 3y + z,

6tz

= −x + 7y + 5z,

x(1) = y(1) = z(1) = 1.

3. Применение формул Дюамеля (2.7) к решению дифференциальных

уравнений

Задача. Пусть ˜x(t) – решение уравнения

L[x] ≡ a

(n)

(t) + a

(n−1)

(t) + . . . + a

x(t) = 1, (3.5)

где a

= const, ∀i = 0, n, удовлетворяющее нулевым начальным услови-

ям

x(0) = x

(0) = . . . = x

(n−1)

(0) = 0. (3.6)

34 Глава I. Основы операционного исчисления

Показать, что решение уравнения

L[x] = f(t), (3.7)

где функция f (t) является оригиналом, удовлетворяющее условиям

(3.6), можно представить в виде

x(t) =

˜x

(τ)f(t − τ) dτ (3.8)

или в виде

x(t) = ˜x(t)f (0) +

(τ)˜x(t − τ) dτ. (3.9)

• Заметим, что результат задачи позволяет находить решение линейно-

го дифференциального уравнения с постоянными коэффициентами при

нулевых начальных условиях, не находя изображения правой части это-

го уравнения.

Пример 9. Найти решение уравнения

(t) + x(t) =

1 + cos

удовлетворяющее условиям: x(0) = x

(0) = 0.

Решение.. Построим решение вспомогательной задачи:

(t) + x(t) = 1, x(0) = x

(0) = 0. (∗)

Соответствующее уравнению (∗) операторное уравнение имеет вид:

X(p) + X(p) =

Откуда получаем

X(p) =

p(p

+ 1)

−

+ 1

↔

1 − cos t.

Таким образом, решением задачи (∗) является функция

˜x(t) = 1 −cos t.

§ 3. Применение преобразования Лапласа 35

С помощью формулы (3.8), учитывая свойство симметричности сверт-

ки, найдем решение заданного уравнения:

x(t) =

1 + cos

· sin (t −τ) dτ.

Вычислив интеграл, получим

x(t) = −

√

sin t ·ln

sin t −

√

sin t +

√

+ cos t ·arctg (cos t) −

cos t. /

• Требование, чтобы начальные условия были нулевыми, является несу-

щественным, так как простой заменой искомой функции задачу с нену-

левыми начальными условиями можно свести к задаче с нулевыми усло-

виями.

Действительно, пусть требуется найти решение уравнения (3.7), удовле-

творяющее ненулевым начальным условиям:

x(0) = x

, x

(0) = x

, . . . , x

(n−1)

(0) = x

n−1

. (3.10)

Выполним замену

x(t) = y(t) + w(t), (3.11)

где y(t) – новая неизвестная функция, а функция w(t) – определена

следующим образом:

w(t) = x

+ x

t +

+ . . . +

n−1

(n − 1)!

n−1

и, очевидно, удовлетворяет условиям:

w(0) = x

, w

(0) = x

, . . . , w

(n−1)

(0) = x

n−1

Тогда задача для уравнения (3.7) с условием (3.10) с помощью замены

(3.11) приводится к следующей: найти решение уравнения

L[y] = f(t) − L[w] ≡ f

(t),

удовлетворяющее нулевым начальным условиям:

y(0) = y

(0) = . . . = y

(n−1)

= 0.

36 Глава I. Основы операционного исчисления

Упражнения

18. Найдите решения уравнений, удовлетворяющие заданным началь-

ным условиям x(0) = x

(0) = 0 :

1) x

(t) − x(t) =

1 + e

; 2) x

(t) − x

(t) =

(1 + e

)

;

3) x

(t) + 2 · x

(t) + x =

−t

1 + t

; 4) x

− x

2 + e

;

5) x

− x

1 + e

; 6) x

+ x =

2 + cos t

§4. Применение преобразования Лапласа к решению

дифференциальных уравнений с запаздывающим

аргументом

Рассмотрим линейное дифференциальное уравнение с запаздываю-

щим аргументом с постоянными коэффициентами:

(n)

(t) =

n−1

k=0

(k)

(t − τ

) + f(t), 0 < t < +∞, (4.1)

где a

= const, τ

= const ≥ 0. Будем считать, что

x(t) = x

(t) = . . . = x

(n−1)

(t) ≡ 0 для ∀t < 0.

Пусть требуется найти решение уравнения (4.1), удовлетворяющее на-

чальным условиям:

x(0) = x

(0) = . . . = x

(n−1)

(0) = 0. (4.2)

Применяя к обеим частям уравнения (4.1) преобразование Лапласа

и учитывая свойство запаздывания оригинала, получим операторное

уравнение для изображения X(p)

↔

x(t) :

X(p) =

n−1

k=0

X(p)e

−τ

+ F (p), (4.3)

где F (p)

↔

f(t). Из (4.3) для X(p) будем иметь:

X(p) =

F (p)

−

n−1

k=0

−τ

. (4.4)

§ 4. Применение преобразования Лапласа 37

Оригинал для изображения (4.4) определяет решение уравнения (4.1),

удовлетворяющее условиям (4.2).

Сформулируем задачу для уравнения с запаздывающим аргумен-

том, описывающую процесс с последействием. Требуется найти непре-

рывно дифференцируемое решение x(t) при t ≥ t

уравнения

(t) = f(t, x(t), x(t −τ)), τ = const > 0, (4.5)

если известно, что

x(t) = φ(t) для t ∈ [t

− τ; t

]. (4.6)

Начальная функция φ(t) – заданная непрерывно дифференцируемая

функция. Отрезок [t

− τ; t

], на котором задается функция φ(t), на-

зывается начальным множеством.

Если уравнение (4.5) является линейным, то его решение, удовлетворя-

ющее условию (4.6), можно найти с помощью преобразования Лапла-

са. Пусть t

= 0, тогда при построении соответствующего операторного

уравнения следует учитывать то, что для изображения функции x(t−τ)

имеем

x(t − τ)

↔

∞

−pt

x(t − τ) dt =

∞

−τ

−p(η+τ)

x(η) dη =

−τ

−p(η+τ)

x(η) dη +

∞

−p(η+ τ )

x(η) dη =

= e

−pτ

−τ

−pη

φ(η) dη + e

−pτ

X(p). (4.7)

При восстановлении оригиналов по известным изображениям можно

воспользоваться следующим разложением:

1 −

γe

−np

(p+a)

= 1+

γe

−np

(p + a)

γe

−np

(p + a)

+. . . =

∞

γe

−np

(p + a)

, (4.8)

которое справедливо для любых n, m ∈ N при условии Re p > 0.

Пример 1. Найти решение уравнения

(t) = x(t −1) + 1, x(0) = 0.

38 Глава I. Основы операционного исчисления

Решение.. Считая, что x(t) ≡ 0 для t ∈ [−1; 0], применение преобра-

зования Лапласа к заданному уравнению дает следующее операторное

уравнение:

pX(p) = X(p)e

−p

Откуда

X(p) =

p − e

−p

1 −

−p

Далее, применяя формулу (4.8), получим

X(p) =

∞

k=0

−p

∞

k=0

−pk

k+2

Учитывая теорему запаздывания, построим выражение для соответ-

ствующего оригинала x(t) в виде:

x(t) =

∞

k=0

(t − k)

k+1

(k + 1)!

χ(t − k).

Оно определяет решение задачи. /

Пример 2. Найти решение уравнения

(t) = x(t −1),

если x(t) ≡ 2 для ∀x ∈ [−1; 0].

Решение.. Пусть x(t)

↔

X(P ). Из условия следует, что x(0) = 2, по-

этому имеем:

(t)

↔

pX(p) − x(0) = pX(p) − 2.

Применим к обеим частям заданного уравнения преобразование Лапла-

са. Для правой части уравнения имеем:

x(t − 1)

↔

∞

−pt

x(t − 1) dt =

∞

−1

−p(z+1)

x(z) dz =

−1

−p(z+1)

x(z) dz +

∞

−p(z+1)

x(z) dz =

= 2

−1

−p(z+1)

dz + e

−p

X(p) =

(1 − e

−p

) + e

−p

X(p).

§ 4. Применение преобразования Лапласа 39

Следовательно, соответствующее операторное уравнение имеет вид:

pX(p) − 2 =

(1 − e

−p

) + e

−p

X(p).

Отсюда получаем:

X(p) = 2 ·

p + 1 − e

−p

− pe

−p

p(p − e

−p

)

Используя результат предыдущего примера, построим оригинал в виде:

x(t) = 2

χ(t) +

∞

k=0

(t − k)

k+1

(k + 1)!

χ(t − k)

. /

Пример 3. Найти решение уравнения

(t) + 2x(t) − x(t − 1) = f(t),

если x(0) = 0 и x(t) ≡ 0 для ∀t < 0.

Решение.. Пусть x(t)

↔

X(p), f(t)

↔

F (p). Так как при заданных усло-

виях x(t − 1)

↔

−p

X(p), то операторное уравнение, соответствующее

заданному, имеет вид:

pX(P ) + 2X(p) − e

−p

X(p) = F(p).

Решение этого уравнения запишем в виде произведения:

X(p) =

p + 2 − e

−p

· F (p).

Построим оригинал для функции:

Y (p) =

p + 2 − e

−p

выполнив следующие преобразования:

Y (p) =

p + 2 − e

−p

p + 2

1 −

−p

p+2

∞

k=0

(p + 2)

k+1

Последнее равенство записано, учитывая формулу (4.8). Переходя

к оригиналам для слагаемых суммы ряда, используя соответствие