Рогачев Г.Н. Построение эмпирических моделей с применением пакета MATLAB. Методические указания к лабораторной работе по курсу Моделирование систем
Подождите немного. Документ загружается.


Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматика и управление в технических системах»
ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ МОДЕЛЕЙ
С ПРИМЕНЕНИЕМ ПАКЕТА MATLAB
Методические указания к лабораторной работе
по курсу "Моделирование систем"
Самара 2005

Составитель: Рогачев Г.Н.
УДК 62-50
Построение эмпирических моделей с применением пакета MATLAB. Методические указания
к лабораторной работе по курсу "Моделирование систем" / Cамар. гос. техн. ун-т; Сост.
Рогачев Г.Н. Самара, 2005. 10 с.
Пособие призвано облегчить выполнение лабораторных работ по дисциплине
«Моделирование систем».
Методические указания предназначены для студентов специальностей 22.01.01
Управление и информатика в технических системах и 22.03.01 Автоматизация
технологических процессов и производств (компьютерные системы управления в
производстве и бизнесе).
Ил. 9.
Печатается по решению редакционно-издательского Совета СамГТУ
2
Лабораторная работа № 1. Построение эмпирических моделей с
применением пакета MATLAB
Цель работы
Научиться строить эмпирические модели в пакете MATLAB.
Теоретические сведения
1. Построение полиномиальной регрессии
Использование пакета MATLAB существенно упрощает расчетную часть
процедуры построения эмпирических моделей, позволяя всецело
сосредоточиться на содержательной стороне решаемой задачи. Рассмотрим
следующий пример.
Предположим, что измерялось количество вещества у, произведенного в
химическом реакторе за единицу времени, при изменении в некотором
диапазоне значений количества катализатора t. Считая, что в данном
химическом процессе существует связь количества произведенной продукции с
количеством внесенного катализатора, построим математическую модель
процесса в виде зависимости у от t.
Введем исходные данные.
>> t=[0 .3 .8 1.1 1.6 2.3]';
>> y=[0.5 0.82 1.14 1.25 1.35 1.40]';
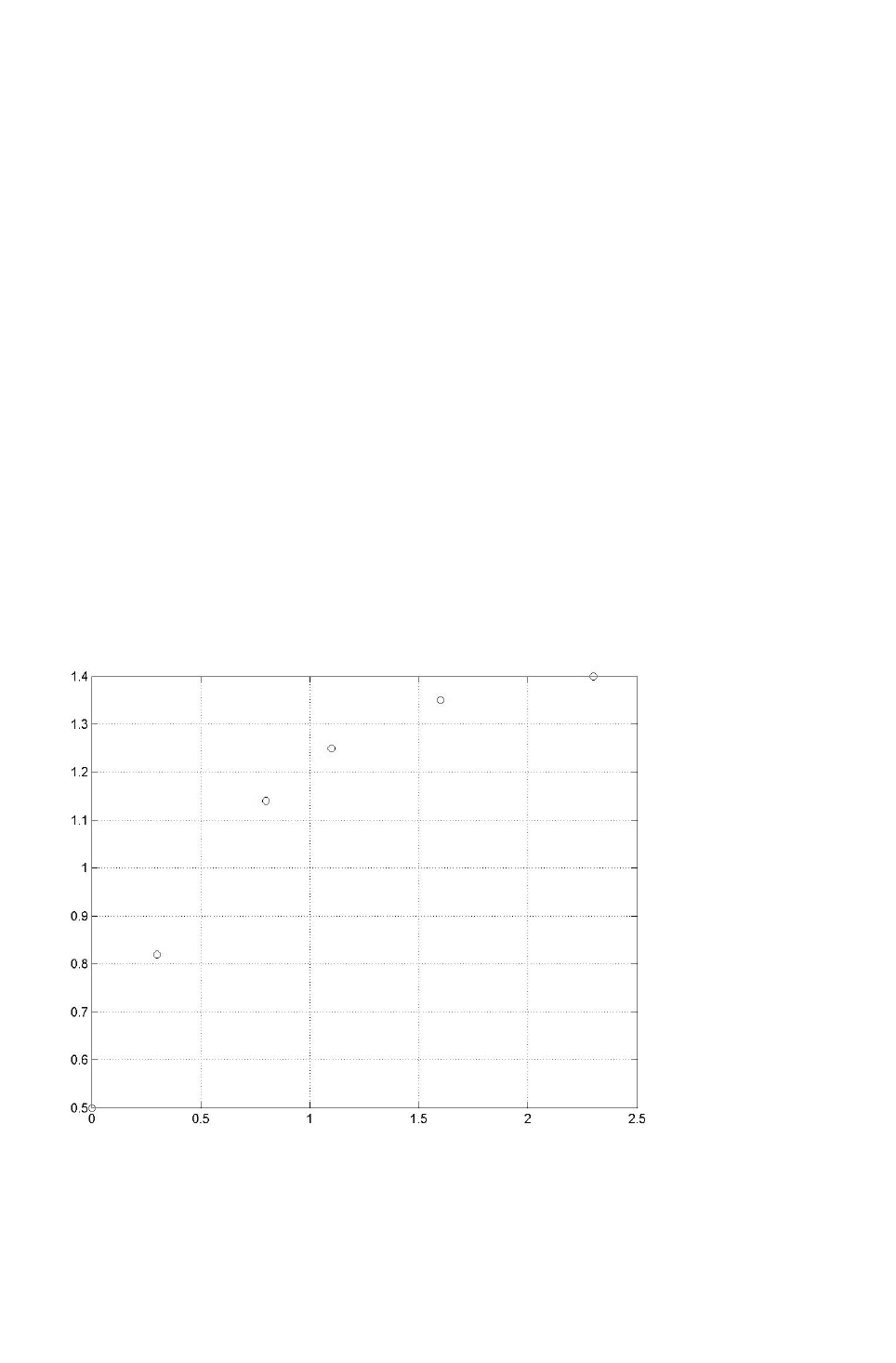
Построим график зависимости количества произведенного вещества y от
количества катализатора t
>> plot(t,y,'o'), grid on
Рис.1. График зависимости количества произведенного вещества у от количества
катализатора t
Прежде чем заниматься построением модели, необходимо убедиться в том, что
между входом t и выходом у имеется взаимосвязь, т. е. выбранная нами в
качестве входной величина действительно оказывает влияние на
интересующую нас выходную величину. Взаимосвязь некоторых зависимостей,
представленных данными (векторами или матрицами), называется корреляцией.
3

Общепринятой мерой этой связи является коэффициент корреляции. Его
близость к 1 указывает на высокую степень такой зависимости.
Выясним, имеется ли какая-то зависимость между переменными t и у.
>> C=corrcoef(t,y)
C=
1.0000 0.9080
0.9080 1.0000
Диагональные элементы C(i,i) представляют дисперсии для столбцов. Не
диагональные элементы C(i,j) представляют ковариации столбцов i и j. В
данном случае зависимость является очень сильной и наше предположение о
влиянии t на у подтвердилось.
Найдем теперь функцию, описывающую отношения между переменными.
Исходя из вида графика рис. 1, можно предположить, что данные могут быть
представлены параболой, т.е. полиномиальной функцией вида y=a
0
+a
1
t+a
2
t
2
.
Нам неизвестны коэффициенты модели а
0
, а
1
и а
2
. Для их определения имеются
шесть уравнений. (Построение эмпирических моделей довольно часто приводит
к переопределенным системам уравнений.) Неизвестные величины можно
вычислить методом наименьших квадратов, минимизируя сумму квадратов
отклонений экспериментальных данных от вычисленных по модели. Используя
оператор \ (backslash или наклонная черта влево), можно легко найти
неизвестные. Сформируем матрицу коэффициентов системы
>> X=[ones(size(t)) t t.^2]
Х =
1.0000 0 0
1.0000 0.3000 0.0900
1.0000 0.8000 0.6400
1.0000 1.1000 1.2100
1.0000 1.6000 2.5600
1.0000 2.3000 5.2900
Решение найдем используя оператор \ (backslash)
>> a=X\y
а =
0.5318
0.9191
-0.2387
Таким образом искомая парабола имеет вид y=0.5318+0.9191t-0.2387t
2
Приведенный график рис. 2 позволяет визуально оценить отклонение
расчетных данных от экспериментальных.
4

Рис. 2. График зависимости количества произведенного вещества у от количества
катализатора t (эксперимент- о, полиномиальная модель-----)
Идентичный результат может быть получен другим способом, а именно за счет
использования команды Tools>Basic Filling графического окна пакета MATLAB
(рис. 3).
Рис. 3. Построение полиномиальной модели при помощи GUI (Graphical User Interface-
Графический Интерфейс Пользователя) Basic Filling пакета MATLAB
Из этих графиков также хорошо видно, что полином второго порядка
аппроксимирует данные со значительной погрешностью. Мы можем увеличить
порядок полинома или исследовать некоторую другую функцию, чтобы
получить лучшую аппроксимацию.
5
Задания
1. Файл census.mat содержит данные о населении США с 1790 по 1990 год.
Командой load census загрузите его. Теперь workspace содержит две
новые переменные: cdate и pop. Первая из них – год, вторая –
соответствующая им численность населения. Найдите модель роста
численности населения, погрешность которой была бы не более 4 млн.
человек.
2. В 2000 году численность населения составила 281 422 тыс. человек.
Найдите ошибку прогноза по найденной модели.
2. Построение линейной по параметрам регрессии
Вместо полиномиальной функции в качестве модели можно попробовать
использовать другую функцию, например экспоненциальную.
Рассмотрим линейную относительно неизвестных параметров модель
следующего вида: y=a
0
+a
1
e
-t
+a
2
tе
-t
. Несмотря на использование трансцендентной
функции, данная модель остается линейной относительно неизвестных
коэффициентов а
0
, a
1
и а
2
, следовательно в вычислительном плане процедура
построения модели не стала сложнее.
Неизвестные коэффициенты вычислим, используя методом наименьших
квадратов. Для этого создадим и решим систему уравнений, формируя матрицу
X и используя оператор \ (backslash).
>> X=[ones(size(t)) exp(-t) t.*exp(-t)];
>> a= X\y
a=
1.3974
-0.8988
0.4097
Следовательно, эта модель имеет вид у=1.3974-0.8988е
-t
+0.4097te
-t
. Теперь
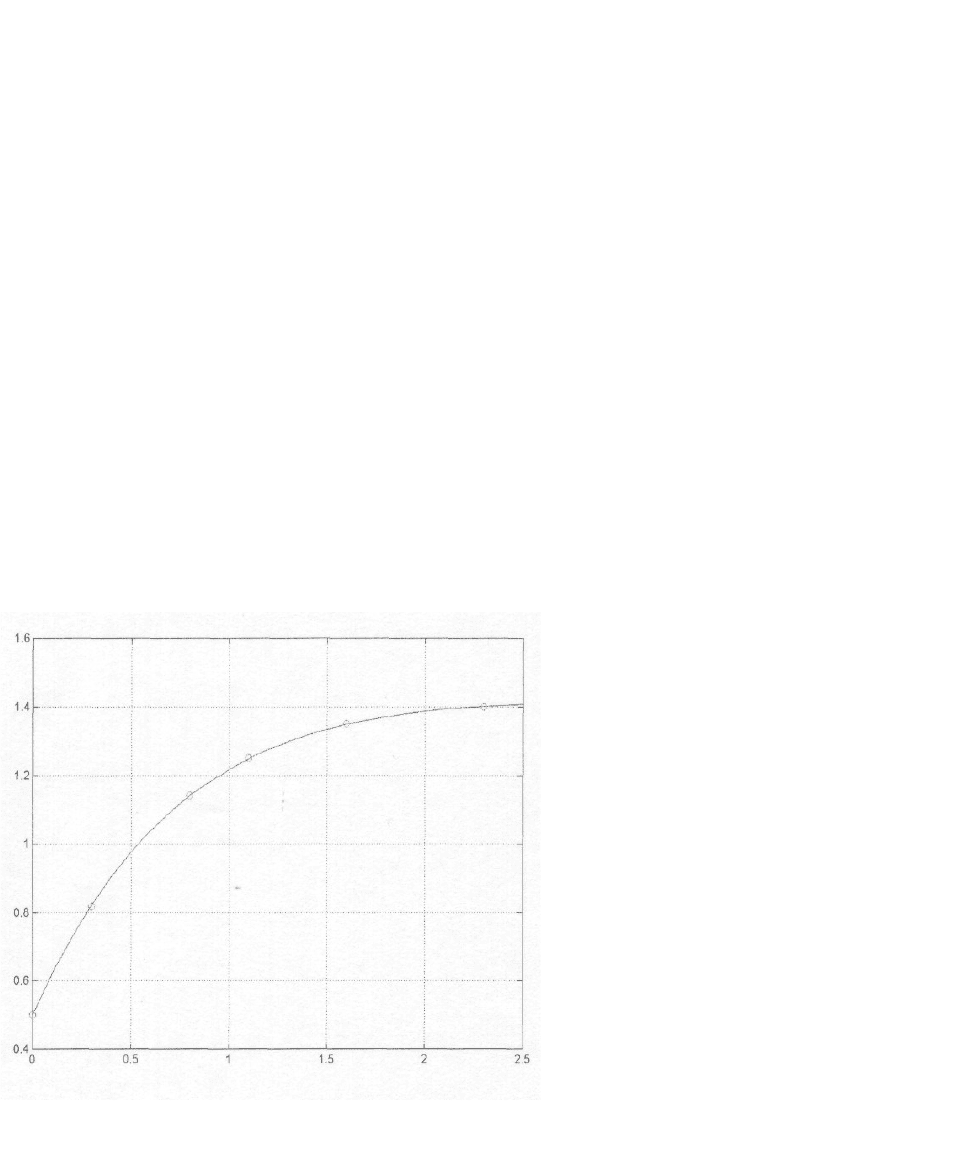
оценим модель по графику рис 4.
Рис. 4. График зависимости количества произведенного вещества у от количества
катализатора t (эксперимент- о, экспоненциальная модель-----)
6

Очевидно, что такая модель намного точнее, чем полиномиальная функция
второго порядка.
Задания
1. Найдите экспоненциальную модель роста численности населения США,
погрешность которой была бы не более 2 млн. человек.
2. В 2000 году численность населения составила 281 422 тыс. человек.
Найдите ошибку прогноза по найденной модели.
3. Построение многомерной регрессии
Если у - функция более чем одной независимой переменной, матричные
уравнения, которые выражают отношение между переменными, могут быть
расширены, чтобы учесть дополнительные данные.
Предположим, что измерялось количество произведенного вещества у для
нескольких значений параметров x
1B
и х
2B
. Наблюдения выглядят следующим
образом
>> x1=[.2 .5 .6 .8 1.0 1.1]';
>> x2=[.1 .3 .4 .9 1.1 1.4]';
>> y =[.17 .26 .28 .23 .27 .24]';
Многомерная регрессионная модель этой системы в простейшем случае
полинома первой степени будет иметь вид
Y=a
o
+a
1
x
1
+a
2
x
2
Неизвестные коэффициенты а
0
, a
1
и а
2
по-прежнему определяются методом
наименьших квадратов. Создадим систему уравнений, формируя
регрессионную матрицу X, и решим ее относительно коэффициентов а
0
, а
1
и а
2
,
используя оператор \ (backslash).
>> x1=[.2 .5 .6 .8 1.0 1.1]';
>> x2=[.1 .3 .4 .9 1.1 1.4]';
>> y =[.17 .26 .28 .23 .27 .24]';
>> X=[ones(size(x1)) x1 x2];
>> a =X\y
>> a=
0.1018
0.4844
-0.2847
Это значит, что модель имеет вид Y=0.1018 + 0.4844х
1
+0.2847х
2
Проверим модель, вычислив максимум модуля отклонения вычисленных
данных от эксперимента
>> Y=X*a;
>> MaxErr= max(abs(Y-y))
MaxErr=
0.0038
Такую максимальную ошибку можно считать удовлетворительной.
Задание
Для исходных данных из части 2, относящихся к зависимости количества
7

произведенного вещества у от значений параметров x
1
и х
2
, построить модель
вида Y=a
o
+a
1
x
1
+a
2
x
2 B
+a
3
x
1
2
+a
4
x
2
2
+a
5
x
1
x
2
4. Построение авторегрессионной модели
Рассмотрим набор экспериментальных данных, представленный на рис 5. Это -
график изменения во времени сигнала на выходе динамической системы.
Рис. 5. График изменения во времени выходной величины у
Используя рассмотренный в лабораторной работе 1 GUI Basic Filling пакета
MATLAB, рассчитаем полиномиальную модель для этого набора данных.
Рис. 6. Построение полиномиальной модели при помощи GUI (Graphical User Interface-
Графический Интерфейс Пользователя) Basic Filling пакета MATLAB
8

Результаты не утешают. Теперь даже десятый порядок полинома дает весьма
значительную погрешность. Что же можно сделать в данном случае?
Заметим, что график этого набора экспериментальных данных весьма сильно
напоминает переходную характеристику колебательного звена или, иначе,
решение дифференциального уравнения второго порядка
ubya
dt
dy
a
dt
yd
a
01
2
2
2
для
)(1 tu
.
Заменим производные на конечные разности по формулам
T
yy
dt
dy
kk 1
,
2
21
2
2
2
T
yyy
dt
yd
kkk
.
или аналогичным. Дифференциальное уравнение второго порядка
преобразуется в разностное уравнение вида
ubyayay
kkk
*
2
*
21
*
1
или иначе
zUbzYzaza
*2*
2
1*
1
1
c подлежащими определению параметрами модели
аP
*PB
1B
,аP
*PB
2,B
bP
*P
Отсюда
ubyayay
kkk
*
2
*
21
*
1
. Теперь хорошо видна связь текущего
значения функции не только с текущим значением аргумента, но и с
предыдущими значениями функции. Таково фундаментальное свойство
динамических систем -«память», т.е. зависимость текущего состояния системы
от предыстории.
Найдем неизвестные коэффициенты а
1
*
, а
2
*
,
b
*
. Для этого используем System
Identification Toolbox. Графический интерфейс пакета System Identification
Toolbox запускается из командной строки командой ident. Запустив его,
импортируем данные.
Оценим параметры модели, задав ее структуру. Для этого в раскрывающемся
списке Estimate (Выбор) остановимся на варианте Parametric models
(Параметрические модели). Данный выбор приведет к открытию диалогового
окна задания структуры модели. По умолчанию пользователю предлагается
ARX-модель (ARX - AutoRegressive with external input - авторегрессионная с
внешним входом). Эта модель описывается следующим образом:
teubububyayay
nbknbkknaknakk
11
*
2
*
1
*
1
*
1
......
где e(t) - белый шум.
Выберем простейший вариант ARX-модели с параметрами na=2, nb=l, nk=0 (nk-
количество звеньев с запаздыванием). Результатом будет агх210-модель.
9
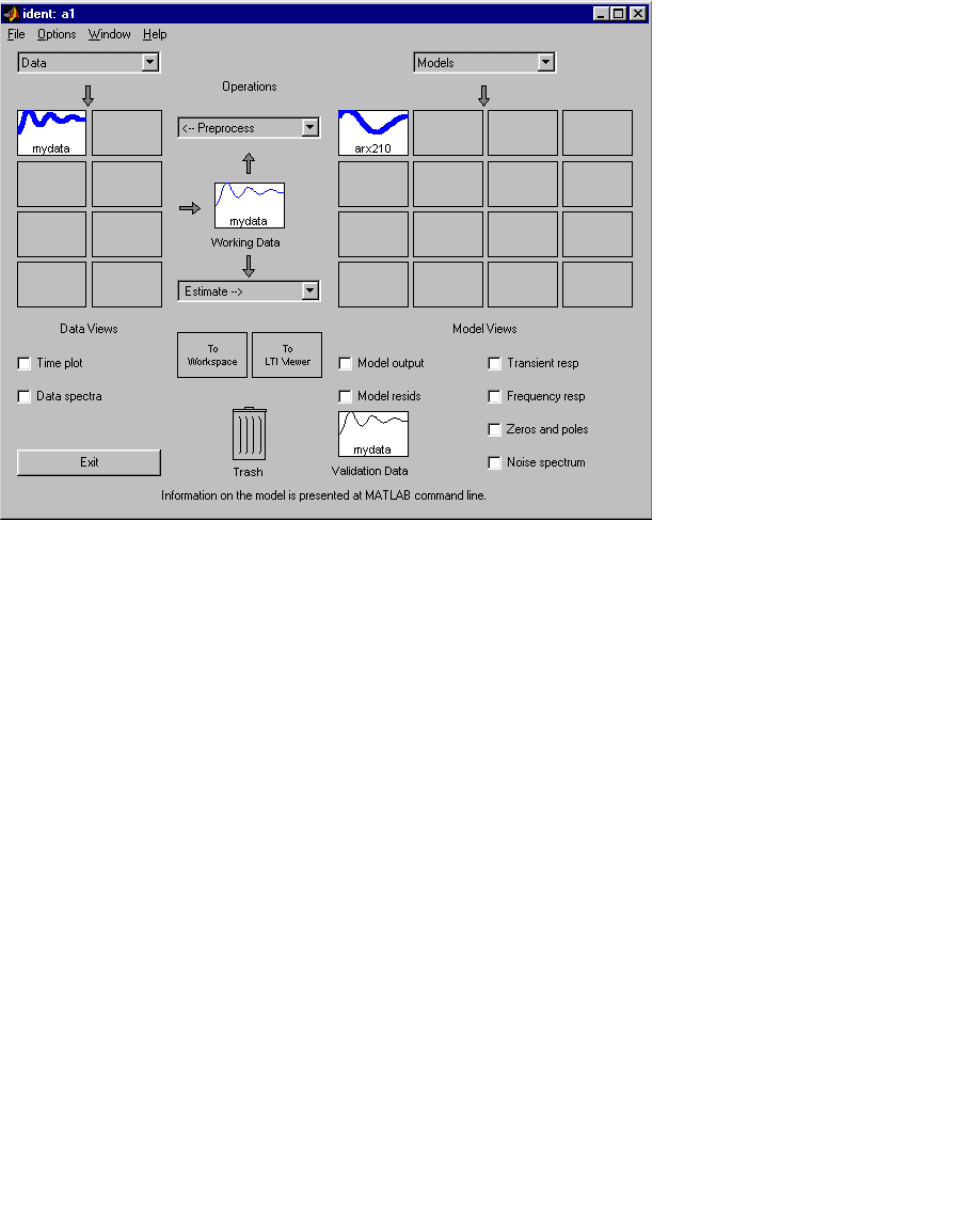
Рис. 7. Построение авторегрессионной модели при помощи GUI System Identification Toolbox
пакета MATLAB
Выполнив команду
>> агх210,
получим следующий отклик пакета MATLAB:
Discrete –time IDPOLY model: A(q)y(t) = B(q)u(t) +e(t)
A(q) =1-1.771 q^-1 +0.9231 q^-2
B(q) =0.1517
Estimated using ARX from data set mydata
Loss function 2.48273e-030 and FPE 2.79307e-030
Sampling interval: 0.4.
Следовательно, полученная модель выглядит так:
uyyy
kkk
1517.09231.0771.1
21
Рассчитаем выходной сигнал ARX-модели.
>> simout1=simout;
>> simout1(3)=0.1517+1.771*simout1(2)-0.9231*simout(1);
>> simout1(4)=0.1517+1.771*simout(3)-0.9231*simout(2);
>> for i=5:51
>> simout1(i)=0.1517+1.771*simout1(i-1)-0.9231*simout(i-2);
>> end;
Построим график изменения во времени выходной величины
10
