Robertson C.R. Fundamental electrical and electronic principles
Подождите немного. Документ загружается.


Electromagnetism
Chapter 5
Learning Outcomes
This chapter concerns the principles and laws governing electromagnetic induction and the
concepts of self and mutual inductance.
On completion of this chapter you should be able to use these principles to:
1 Understand the basic operating principles of motors and generators.
2 Carry out simple calculations involving the generation of voltage, and the production of
force and torque.
3 Appreciate the signifi cance of eddy current loss.
4 Determine the value of inductors, and apply the concepts of self and mutual inductance to
the operating principles of transformers.
5 Calculate the energy stored in a magnetic fi eld.
6 Explain the principle of the moving coil meter, and carry out simple calculations for the
instrument.
7 Describe the operation of a wattmeter and simple ohmmeter.
141
5.1 Faraday ’ s Law of Electromagnetic Induction
It is mainly due to the pioneering work of Michael Faraday, in the
nineteenth century, that the modern technological world exists as
we know it. Without the development of the generation of electrical
power, such advances would have been impossible. Thus, although the
concepts involved with electromagnetic induction are very simple, they
have far-reaching infl uence. Faraday ’ s law is best considered in two
interrelated parts:
1 The value of emf induced in a circuit or conductor is directly
proportional to the rate of change of magnetic fl ux linking with it.
2 The polarity of such an emf, induced by an increasing fl ux, is
opposite to that induced by a decreasing fl ux.
142
Fundamental Electrical and Electronic Principles
The key to electromagnetic induction is contained in part one of the
law quoted above. Here, the words ‘ rate of change ’ are used. If there is
no change in fl ux, or the way in which this fl ux links with a conductor,
then no emf will be induced. The proof of the law can be very simply
demonstrated. Consider a coil of wire, a permanent bar magnet and a
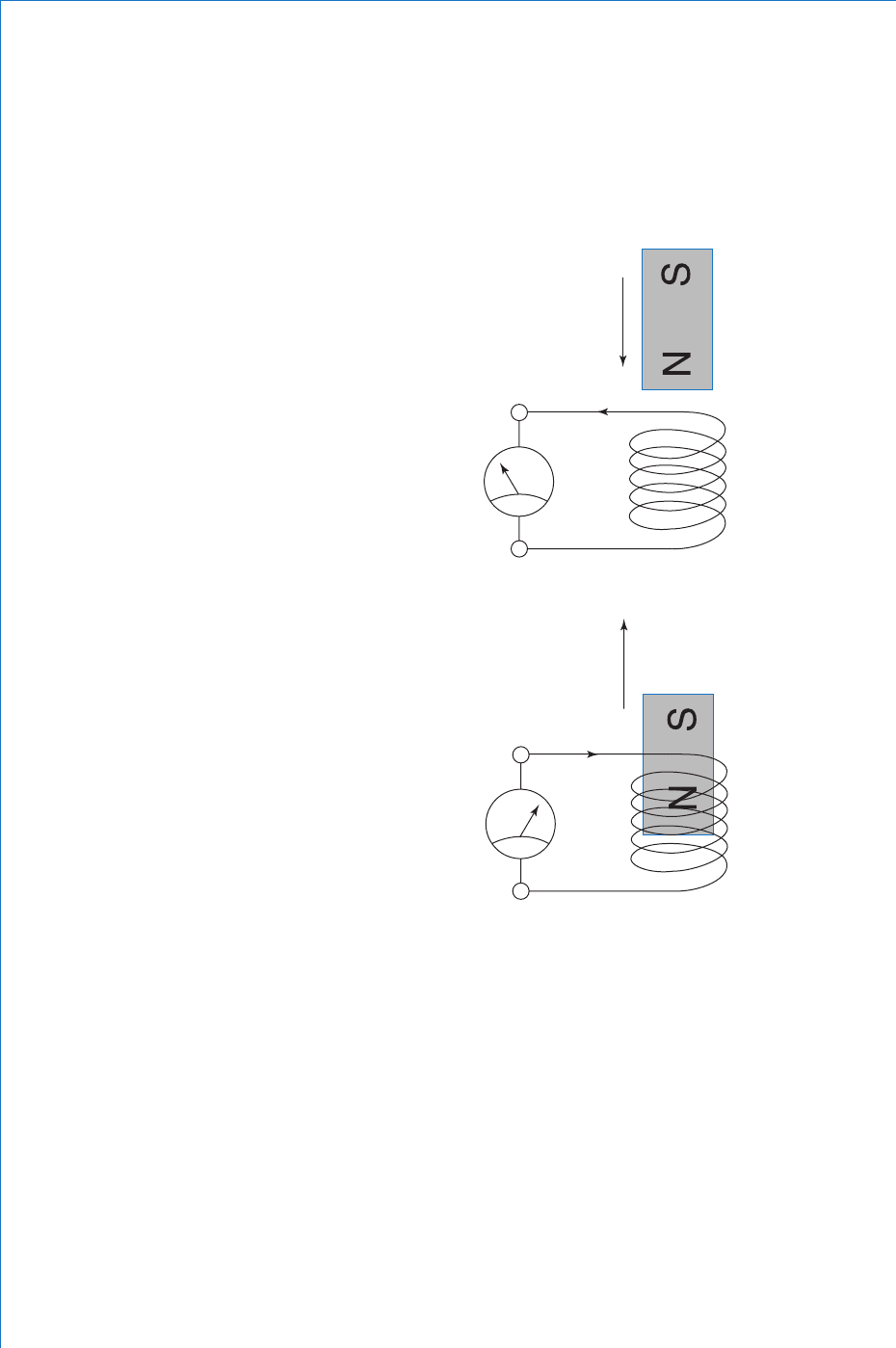
galvanometer as illustrated in Figs. 5.1 and 5.2 .
Consider the magnet being moved so that it enters the centre of
the coil. When this is done it will be seen that the pointer of the
galvo defl ects in one direction. This defl ection of the pointer is only
momentary, since it only occurs whilst the magnet is moving. The
galvo is of course a current measuring device. However, any current
fl owing through it must be due to a voltage between its terminals. Since
there is no other source of emf in the circuit, then it must be concluded
that an emf has been induced or created in the coil itself. The resulting
current indicated by the galvo depends on the value of this emf. It will
also be observed that when the magnet is stationary (either inside or
outside the coil) the galvo does not defl ect. Hence, emf is induced into
the coil only when the magnet is in motion.
Fig. 5.1
Fig. 5.2

Electromagnetism
143
When the magnet is withdrawn from the coil, the galvo will again be
seen to defl ect momentarily. This time, the defl ection will be in the
opposite direction. Provided that the magnet is removed at the same
rate as it was inserted, then the magnitudes of the defl ections will be
the same. The polarities of the induced emfs will be opposite to each
other, since the current fl ow is reversed. Thus far, we have confi rmation
that an emf is induced in the coil when a magnetic fl ux is moving
relative to it. We also have confi rmation of part two of the law.
In order to deduce the relationship between the value of induced
emf and the rate of change of fl ux, the magnet needs to be moved at
different speeds into and out of the coil. When this is done, and the
resulting magnitudes of the galvo defl ection noted, it will be found that
the faster the movement, the greater the induced emf.
This simple experiment can be further extended in three ways. If the
magnet is replaced by a more powerful one, it will be found that for
the same speed of movement, the corresponding emf will be greater.
Similarly, if the coil is replaced with one having more turns, then for a
given magnet and speed of movement, the value of the emf will again be
found to be greater. Finally, if the magnet is held stationary within the
coil, and the coil is then moved away, it will be found that an
emf is once more induced in the coil. In this last case, it will also be
found the emf has the same polarity as obtained when the magnet was
fi rst inserted into the stationary coil. This last effect illustrates the point
that it is the relative movement between the coil and the fl ux that induces
the emf.
The experimental procedure described above is purely qualitative.
However, if it was refi ned and performed under controlled conditions,
then it would yield the following results:
The magnitude of the induced emf is directly proportional to the value
of magnetic fl ux, the rate at which this fl ux links with the coil, and the
number of turns on the coil. Expressed as an equation we have:
e
N
t
d
d
volt
(5.1)
Notes:
1
The symbol for the induced emf is shown as a lower-case letter e.
This is because it is only present for the short interval of time
during which there is relative movement taking place, and so has
only a momentary value.
2 The term d /d t is simply a mathematical means of stating ‘ the
rate of change of fl ux with time ’ . The combination N/ d t is often
referred to as the ‘ rate of change of fl ux linkages ’ .
3 The minus sign is a reminder that Lenz ’ s law applies. This law is
described in the next section.

144
Fundamental Electrical and Electronic Principles
4 Equation (5.1) forms the basis for the defi nition of the unit of
magnetic fl ux, the weber, thus:
The weber is that magnetic fl ux which, linking a circuit of one turn,
induces in it an emf of one volt when the fl ux is reduced to zero at a
uniform rate in one second.
In other words, 1 volt 1 weber/second or 1 weber 1 volt second.
5.2 Lenz ’ s Law
This law states that the polarity of an induced emf is always such that it
opposes the change which produced it. This is similar to the statement
in mechanics, that for every force there is an opposite reaction.
5.3 Fleming ’ s Righthand Rule
This is a convenient means of determining the polarity of an induced emf
in a conductor. Also, provided that the conductor forms part of a complete
circuit, it will indicate the direction of the resulting current fl ow.
The fi rst fi nger, the second fi nger and the thumb of the right hand are
held out mutually at right angles to each other (like the three edges of
a cube as shown in Fig. 5.3 ). The F irst fi nger indicates the direction of
the F lux, the thu M b the direction of M otion of the conductor relative
to the fl ux, and the s EC ond fi nger indicates the polarity of the induced
E mf, and direction of Current fl ow. This process is illustrated in
Fig. 5.4 , which shows the cross-section of a conductor being
thuMb
seCond finger
first finger
Fig. 5.3
v
x
Fig. 5.4
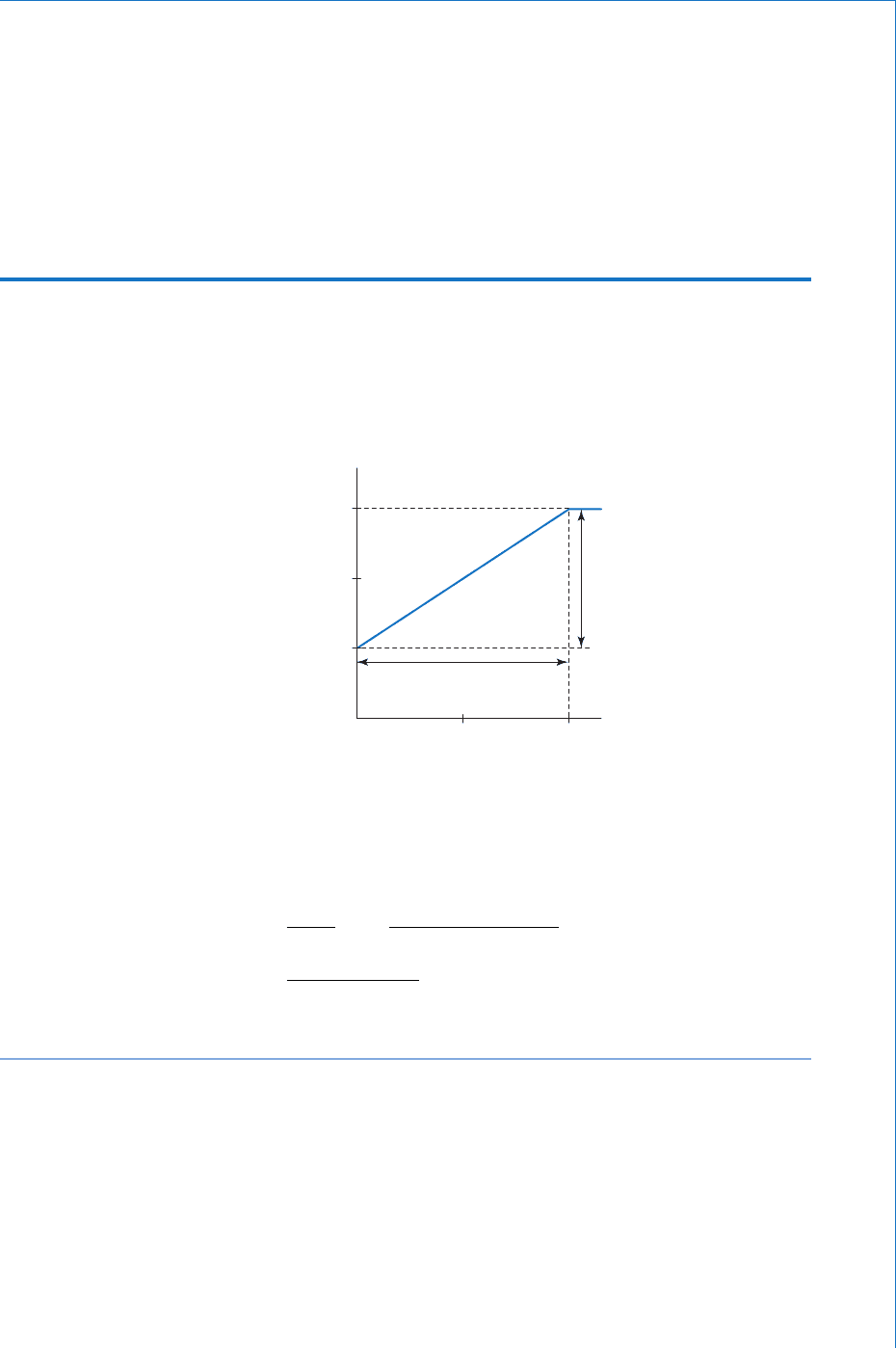
Electromagnetism
145
moved vertically upwards at a constant velocity through the magnetic
fi eld.
Note: The thumb indicates the direction of motion of the conductor
relative to the fl ux. Thus, the same result would be obtained from the
arrangement of Fig. 5.4 if the conductor was kept stationary and the
magnetic fi eld was moved down.
Worked Example 5.1
Q T h e ux linking a 100 turn coil changes from 5 mWb to 15 mWb in a time of 2 ms. Calculate the average
emf induced in the coil; see Fig. 5.5 .
15
10
5
01
dt
t(ms)
dΦ
Φ(mWb)
2
Fig. 5.5
A
N 100; d (15 5) 10
3
Wb; d t 2 10
3
s
e
N
t
e
d
d
volt
so
11 1
1
111
1
00 5 5 0
20
0000
20
3
3
3
3
()
500 V Ans
Note that if the fl ux was reduced from 15 mWb to 5 mWb, then the
term shown in brackets above would be 10. The resulting emf would
be 500 V. When quoting equation (5.1), the minus sign should always
be included. However, since it is often the magnitude of the induced
emf that is more important, it is normal practice to ignore the minus
sign in the subsequent calculation. One of the major exceptions to this
practice arises when considering the principles of operation of the
transformer.
146
Fundamental Electrical and Electronic Principles
Worked Example 5.2
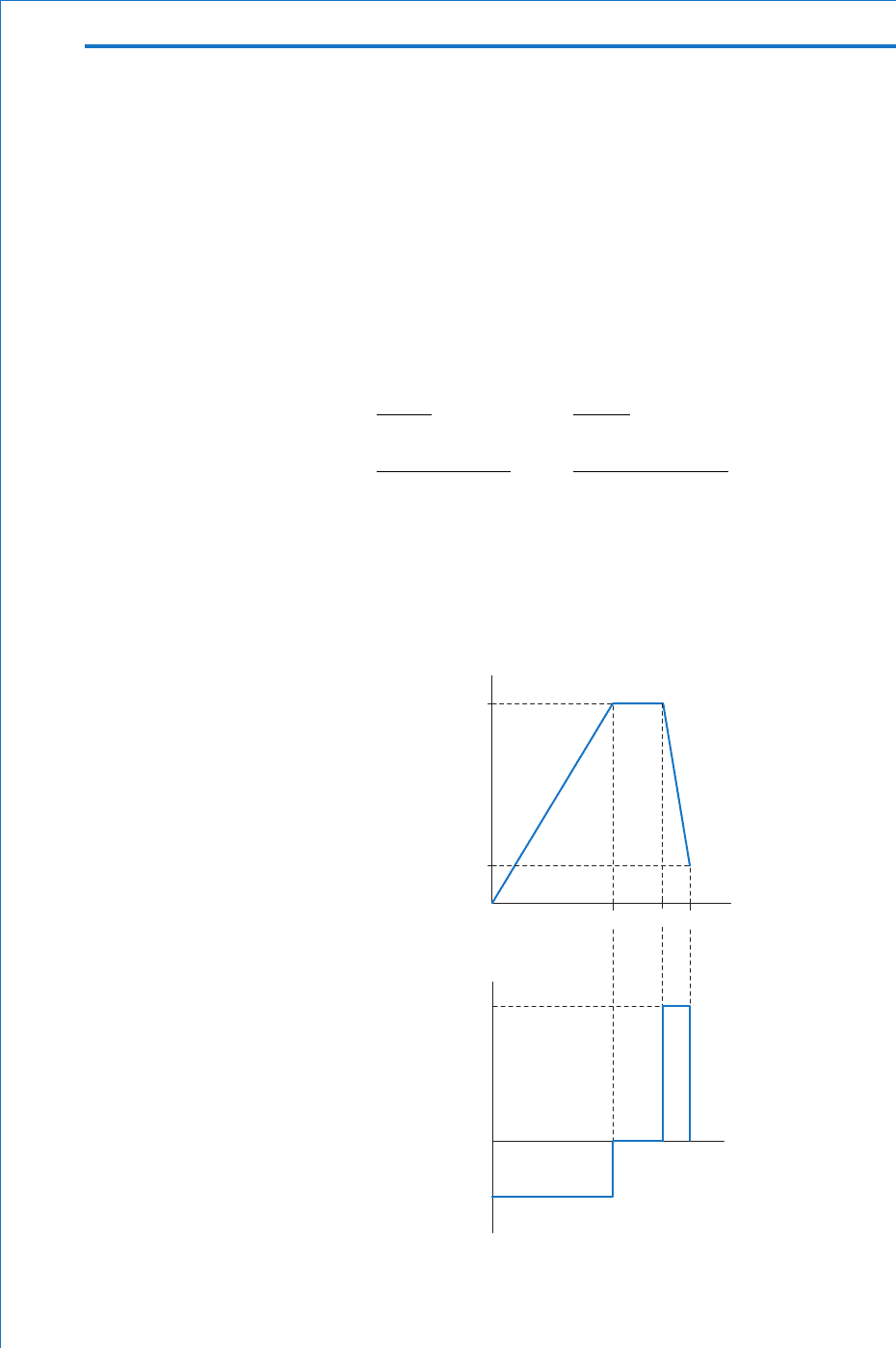
Q A 250 turn coil is linked by a magnetic ux that varies as follows: an increase from zero to 20 mWb in
a time of 0.05 s; constant at this value for 0.02 s; followed by a decrease to 4 mWb in a time of 0.01 s .
Assuming that these changes are uniform, draw a sketch graph (i.e. not to an accurate scale) of the
variation of the ux and the corresponding emf induced in the coil, showing all principal values.
A
Firstly, the values of induced emf must be calculated for those periods when the
ux changes.
d
1
(20 0) 10
3
Wb; d t
1
0.05 s
d
2
(4 20) 10
3
Wb; d t
2
0.01 s
e
N
t
e
N
t
1
1
1
1
d
d
volt and
d
d
volt
2
2
2
3
250 20 0
005
250
.
( 111
1
1
1
60
00
00 400
3
2
)
.
so V and Vee
The resulting sketch graph is shown in Fig. 5.6 .
20
4
0
400
100
0
e (V)
t(ms)
t(ms)
Φ(mWb)
50 70 80
Fig. 5.6

Electromagnetism
147
Worked Example 5.3
Q A coil when linked by a ux which changes at the rate of 0.1 Wb/s, has induced in it an emf of 10 0 V .
Determine the number of turns on the coil.
A
e
t
1100 V;
d
d
Wb/s
0.
e
N
t
N
e
t
N
d
d volt
so
d/d
turns
1
1
1
00
0
000
.
Ans
Note that the minus sign has been ignored in the calculation. A negative
value for number of turns makes no sense.
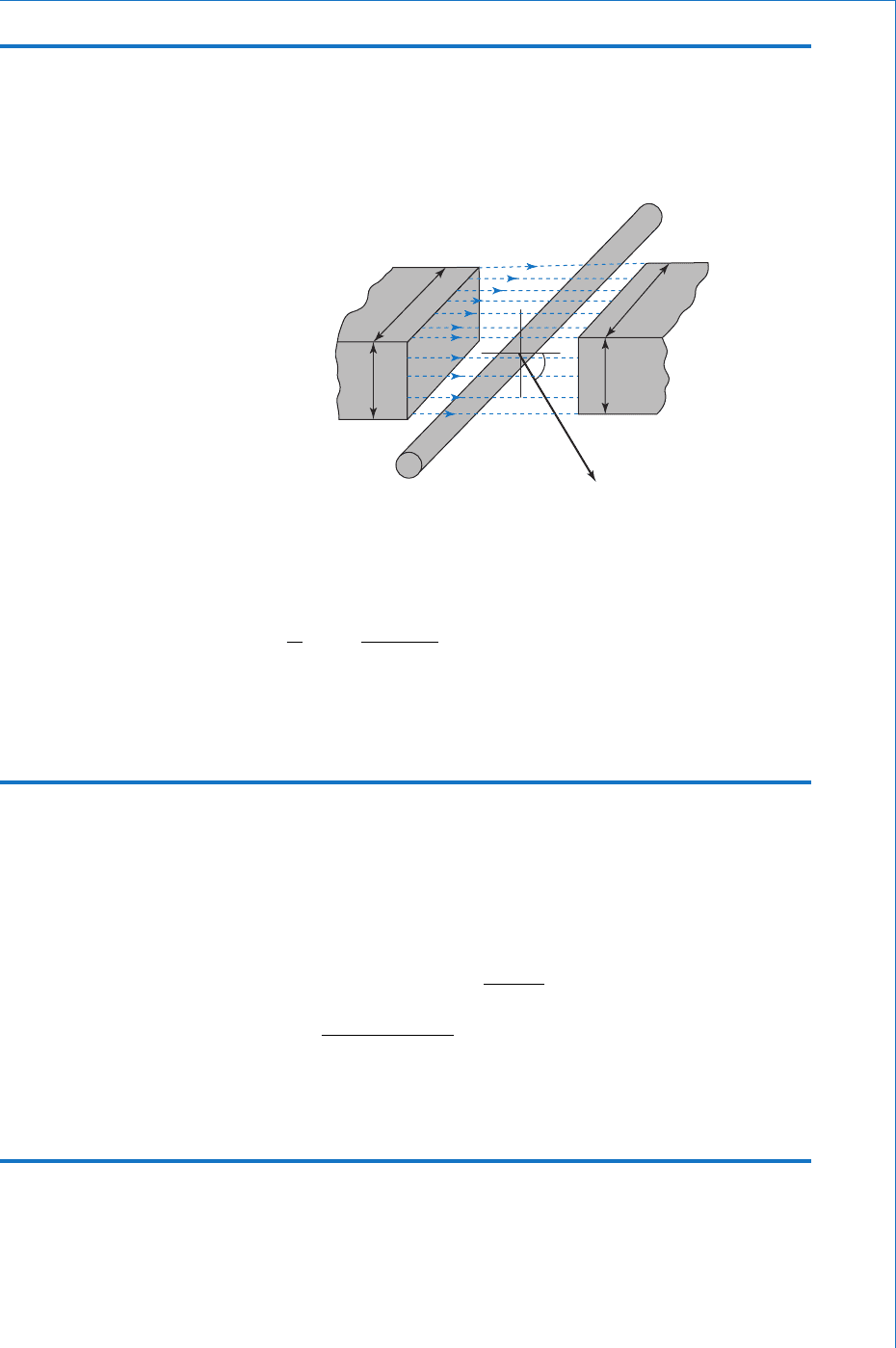
5.4 EMF Induced in a Single Straight Conductor
Consider a conductor moving at a constant velocity v metre per second
at right angles to a magnetic fi eld having the dimensions shown in
Fig. 5.7 . The direction of the induced emf may be obtained using
Fleming ’ s righthand rule, and is shown in the diagram. Equation (5.1)
is applicable, and in this case, the value for N is 1.
d
V
Fig. 5.7
Thus,
d
d
volt, and since is constant
then volt
but
e
t
e
t
BA
e
BA
t
weber
so
148
Fundamental Electrical and Electronic Principles
also, the csa of the fi eld, A d metre
2
so
e
Bd
t
and since
d
t
v velocity ,
then
eBv volt
(5.2)
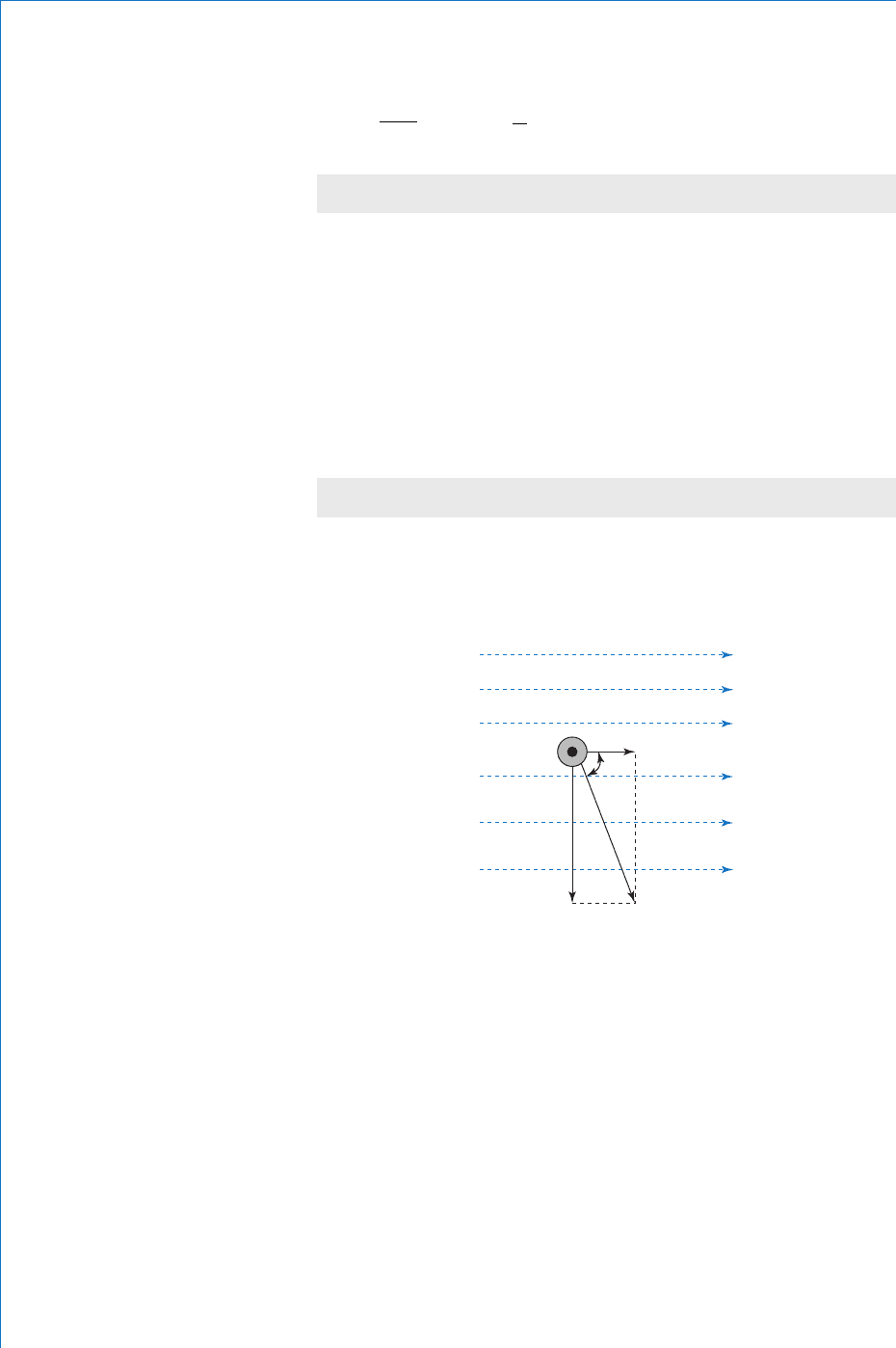
The above equation is only true for the case when the conductor is
moving at right angles to the magnetic fi eld. If the conductor moves
through the fi eld at some angle less than 90°, then the ‘ cutting ’
action between the conductor and the fl ux is reduced. This results in
a consequent reduction in the induced emf. Thus, if the conductor
is moved horizontally through the fi eld, the ‘ cutting ’ action is zero,
and so no emf is induced. To be more precise, we can say that only
the component of the velocity at 90° to the fl ux is responsible for the
induced emf. In general therefore, the induced emf is given by:
eBv sin volt
(5.3)
where v sin is the component of velocity at 90° to the fi eld, as
illustrated in Fig. 5.8 .
v sinθ
θ
v cosθ
v
Fig. 5.8
This equation is simply confi rmed by considering the previous two
extremes; i.e. when conductor moves parallel to the fl ux, 0°; sin
0; so e 0. When it moves at right angles to the fl ux, 90°;
sin 1; so we are back to equation (5.2).
Note: is known as the effective length of the conductor, since it is
that portion of the conductor that actually links with the fl ux. The total
length of the conductor may be considerably greater than this, but
those portions that may extend beyond the fi eld at either end will not
have any emf induced.
Electromagnetism
149
Worked Example 5.4
Q A conductor is moved at a velocity of 5 m/s at an angle of 60° to a uniform magnetic eld of 1. 6 m W b .
The eld is produced by a pair of pole pieces, the faces of which measure 10 cm by 4 cm. If the
conductor length is parallel to the longer side of the eld, calculate the emf induced; see Fig. 5.9 .
d
5 m/s
4 cm
10 cm
60°
Fig. 5.9
A
v 5 m/s; u 60°; 1.6 10
3
Wb; ℓ 0.1 m ; d 0.04 m (see Fig. 5.9 )
B
A
eBv
tesla T
sin volt s
11
1
1
.
..
.
..
60
0004
04
04 0 5
3
ii n
so V
60
073
e .1 Ans
Worked Example 5.5
Q A conductor of e ective length 15 cm, when moved at a velocity of 8 m/s at an angle of 55° to a
uniform magnetic eld, generates an emf of 2.5 V. Determine the density of the eld.
A
ℓ 0.15 m ; v 8 m/s; u 55°; e 2.5 V
eBv B
e
v
B
sin volt, so
sin
tesla
hence,
si
25
05 8
.
.1
nn
T
55
2 543
B . Ans
Worked Example 5.6
Q The axle of a lorry is 2.2 m long, and the vertical component of the Earth ’ s magnetic eld density,
through which the lorry is travelling, is 38 T. If the speed of the lorry is 80 km/h, then calculate the
emf induced in the axle.

150
Fundamental Electrical and Electronic Principles
A
ℓ 2.2 m;
v
80 0
60 60
3
1
m/s
; B 38 10
6
T; sin u 1, since u 90°
eBv
e
sin volt
so, mV
38 0 2 2 80 0
3600
86
63
11
1
.
. Ans
This section, covering the induction or generation of an emf in a
conductor moving through a magnetic fi eld, forms the basis of the
generator principle. However, most electrical generators are rotating
machines, and we have so far considered only linear motion of the
conductor.
Consider the conductor now formed into the shape of a rectangular
loop, mounted on to an axle. This arrangement is then rotated between
the poles of a permanent magnet. We now have the basis of a simple
generator as illustrated in Fig. 5.10 .
Fig. 5.10
(a) (b)
The two sides of the loop that are parallel to the pole faces will each
have an effective length metre. At any instant of time, these sides
are passing through the fi eld in opposite directions. Applying the
righthand rule at the instant shown in Fig. 5.10 , the directions of
the induced emfs will be as marked, i.e. of opposite polarities.
However, if we trace the path around the loop, it will be seen that
both emfs are causing current to fl ow in the same direction around
the loop. This is equivalent to two cells connected in series as
shown in Fig. 5.11 .
The situation shown in Fig. 5.10 applies only to one instant in one
revolution of the loop (it is equivalent to a ‘ snapshot ’ at that instant).
