Research on oil recovery mechanisms in heavy oil reservoirs
Подождите немного. Документ загружается.

222
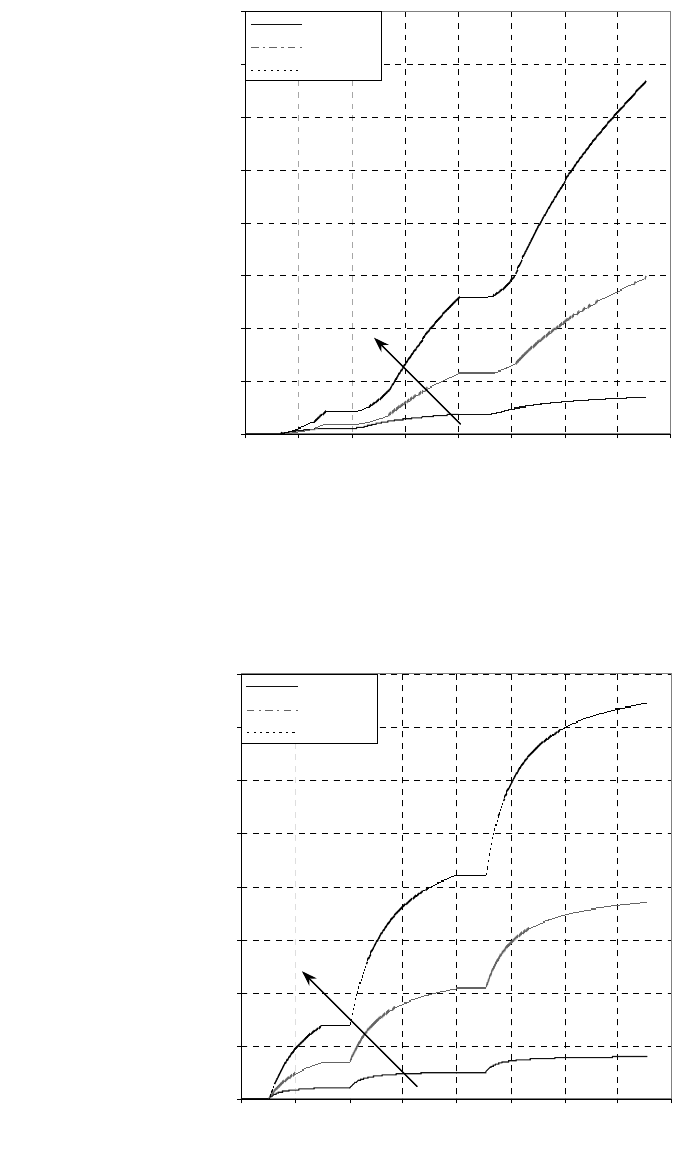
Fig.7 Sensitivity to steam injection rate (a) Cumulative oil production versus
cumulative time (b) Cumulative water production versus cumulative time (c)
Average steam zone temperature versus cumulative time (d) Steam zone volume
versus cumulative time
7(a)
0
1000
2000
3000
4000
5000
6000
7000
8000
0 50 100 150 200 250 300 350 400
Cumulative Time (days)
Cumulative Oil Production (STB/ft)
1.0 STB/D
5.0 STB/D
10.0 STB/D
0
200
400
600
800
1000
1200
1400
1600
0 50 100 150 200 250 300 350 400
Cumulative Time (days)
Cumulative Water Production (STB/ft)
1.0 STB/D
5.0 STB/D
10.0 STB/D
7(b)

223
0
50
100
150
200
250
300
350
400
0 50 100 150 200 250 300 350 400
Cumulative Time (days)
Temperature (
o
F)
1.0 STB/D
5.0 STB/D
10.0 STB/D
7(c)
0
1000
2000
3000
4000
5000
6000
7000
8000
0 50 100 150 200 250 300 350 400
Cumulative Time (days)
Volume of Heated Zone (ft
3
/ft)
1.0 STB/D
5.0 STB/D
10.0 STB/D
7(d)
Fig.7 Sensitivity to steam injection rate: (a) cumulative oil production versus cumulative time,
(b) cumulative water production versus cumulative time, (c) average steam zone temperature
versus cumulative time, (d) steam zone volume versus cumulative time
224
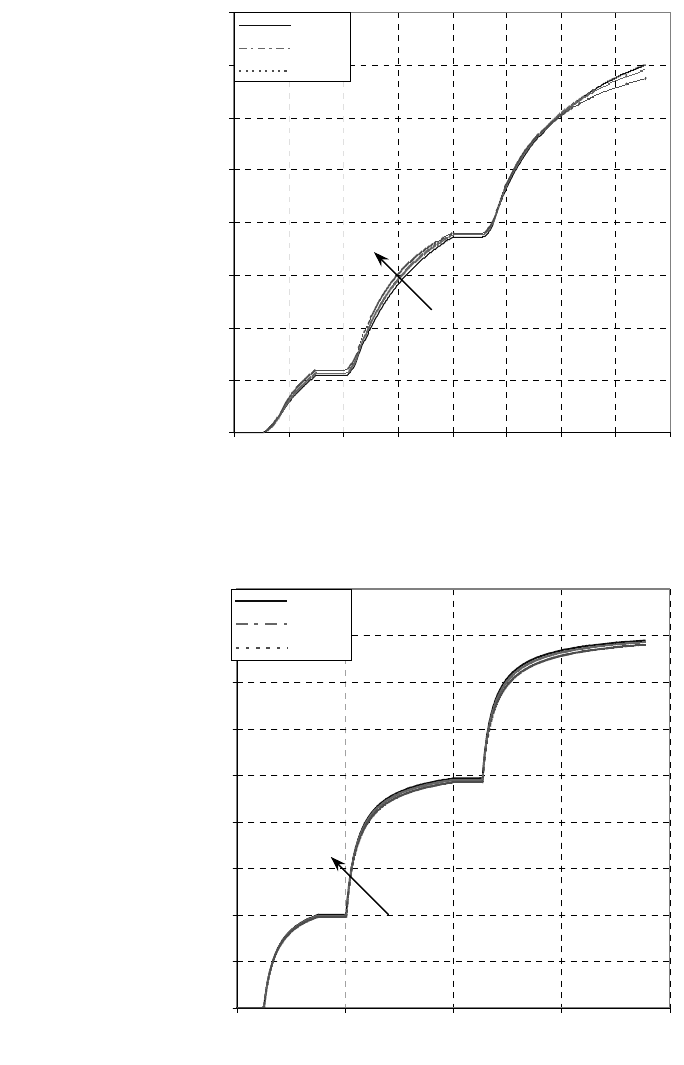
Fig.8 Sensitivity to bottom-hole pressure (a) Cumulative oil production versus
cumulative time (b) Cumulative water production versus cumulative time (c)
Average steam zone temperature versus cumulative time (d) Steam zone volume
versus cumulative time
8(a)
0
100
200
300
400
500
600
700
800
0 50 100 150 200 250 300 350 400
Cumulative Time (days)
Cumulative Oil Production (STB/ft)
150 psia
200 psia
300 psia
0
20
40
60
80
100
120
140
160
180
0 100 200 300 400
Cumulative Time (days)
Cumulative Water Production (STB/ft)
150 psia
200 psia
300 psia
8(b)

225
0
50
100
150
200
250
300
350
400
450
0 50 100 150 200 250 300 350 400
Cumulative Time (days)
Temperature (
o
F)
150 psia
200 psia
300 psia
8(c)
0
50
100
150
200
250
300
350
400
450
500
0 50 100 150 200 250 300 350 400
Cumulative Time (days)
Heated Zone Volume (ft
3
/ft)
150 psia
200 psia
300 psia
8(d)
Fig.8 Sensitivity to bottom-hole pressure: (a) cumulative oil production versus cumulative time,
(b) cumulative water production versus cumulative time, (c) average steam zone temperature
versus cumulative time, (d) steam zone volume versus cumulative time
226
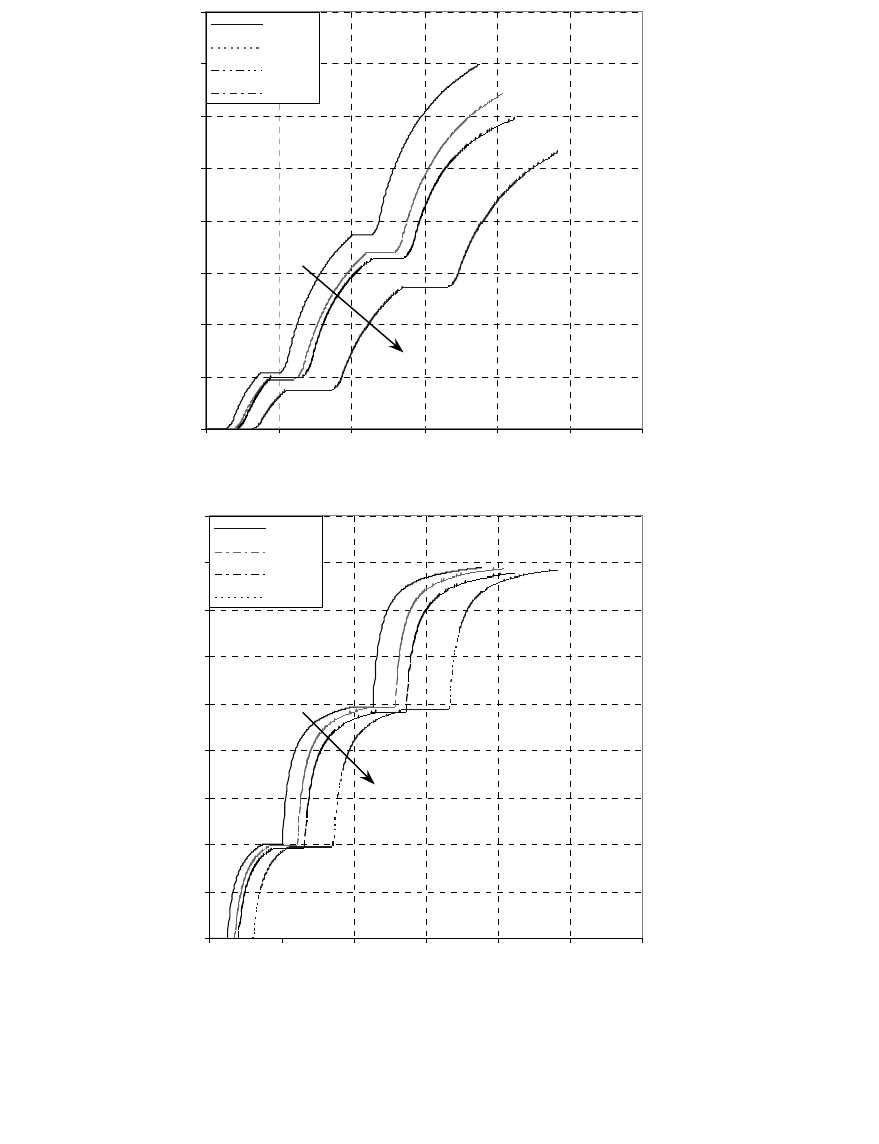
Fig.9 Sensitivity to soaking interval
(a) Cumulative oil production versus
cumulative time (b) Cumulative water production versus cumulative time
9(a)
0
20
40
60
80
100
120
140
160
180
0 100 200 300 400 500 600
Cumulative Time (days)
Cumulative Water Production (STB/ft)
15 days
25 days
30 days
50 days
9(b)
0
100
200
300
400
500
600
700
800
0 100 200 300 400 500 600
Cumulative Time (days)
Cumulative Oil Production (STB/ft)
15 days
25 days
30 days
50 days
Fig.9 Sensitivity to soaking interval: (a) cumulative oil production versus cumulative time (b)
cumulative water production versus cumulative time

227
Appendix A
Derivation for calculating
f
HD
The heat transfer model for conduction cooling of the heated zone can be solved for the horizontal
and vertical conduction mechanisms. We have solved the horizontal heat transfer mechanism
problem. When conduction occurs as described, the temperature at any point within the heated
geometry can be expressed as the product:
Rs
zx
TTV
V
−=
=
ννν
(A-1)
where,
ν
x
and
ν
z
are unit solutions of component conduction problems in the
x
and
z
directions,
respectively. Similarly, an integrated average temperature for the heated regions may be computed
as:
zx
V
ννν
=
(A-2)
The average unit solution for
x
ν
is obtained by solving the one-dimensional heat conduction
problem in the horizontal direction:
t
x
xx
∂
∂
=
∂
∂
νν
α
2
2
(A-3)
Initial and Boundary conditions:
1.
ν
x
= 1 ; t = t
init
; 0 < x < a
2.
ν
x
= 0 ; t = t
init
; |x| > a
3.
ν
x
= 0 ; t
≥
t
init
; x
→
∞
4.
Carlslaw and Jaeger have given the solution for the problem at hand with the boundary condition
specified as:
+
+
−
=
t
xa
erfc
t
xa
erfc
x
αα
ν
22
2
1
(A-4)
This solution holds at any vertical distance ‘ y ’ upwards from the horizontal well as shown in the
figure. To find the average
x
ν
over the entire triangular heated area, we have,
∫
∫
=
A
A
x
x
dA
dA
0
0
ν
ν
(A-5)
If we take an elementary strip parallel to the x-axis, we will be integrating the given function with
respect to x. The ends of this strip are bounded by the lines x = (b/h
t
).y and x = -(b/h
t
).y; so that
228
these are the limits of integration with respect to x. Next, we integrate with respect to y from y = 0
to y = h
t
. This, therefore, covers the whole area of the triangle.
Thus, the integral reduces to:
∫∫
∫∫
−
−
=
y
h
b
y
h
b
h
y
h
b
y
h
b
h
x
x
t
t
t
t
t
t
dxdy
dxdy
0
0
ν
ν
(A-6)
The final integration result is:
+
−
+
−+−+=
2
1
1
211
exp0.2
2
1
DH
DH
DH
DH
x
t
t
erf
t
t
π
π
ν
(A-7)
where,
(
)
2
h
inj
DH
R
tt
t
−
=
α
(A-8)
R
h
is the horizontal range of the extent of the steam zone and is given by,
()
θ
cot
th
hR =
(A-9)
245
4.2 PSEUDOSTEADY STATE FLOW
(William E. Brigham)
ABSTRACT
Whenever a closed system is being produced at a constant rate, after a period of time the
entire system starts to be depleted. This depletion rate is constant everywhere in the system. This
state of dynamic equilibrium is usually called pseudosteady state flow, for the forms of the
equations look a great deal like their steady state equivalents.
These equation forms follow the diffusivity equation. However, they can be derived
without using that equation, but rather, by integrating Darcy’s Law and by invoking the overall
material balance equation. The forms of these equations can be examined for all three of the
geometries commonly used by reservoir engineers; linear, radial and spherical. These solutions are
found to be imbedded in the published transient equations for these geometries. However, these
transient results are written in such a way that it is not obvious that these concepts have been
included in them.
Thus the results seen in these notes are not new. But, in the form presented, they give great
insight on the nature of these flow equations, and the concepts leading up to them. It is always
useful to clarify concepts of this sort.
INTRODUCTION
I have written a series of notes for steady state flow, and for successions of steady states
(Brigham, 1987). I’m going to deviate from that scenario to discuss transient flow in closed
bounded systems. This is flow that follows the diffusivity equation; however, in discussing this
type of flow behavior, the diffusivity equation will not need to be used.
PSEUDOSTEADY STATE CONCEPTS
If we have a well producing at a constant rate in a closed system, the pressure at the well
drops with time; also the effect of flow at the well is to cause the pressure drop to move further into
the reservoir with time. After a period of time the effect of the well is seen at the outer boundary.
Since it is a closed system, with no flow at the outer boundary, the pressure gradient there must be
zero. However, since the well is depleting the reservoir, the pressure must drop there with time just
as it does in the remainder of the reservoir.
After a period of time in this closed system, a state of dynamic equilibrium is reached where
the well begins to deplete the entire reservoir. From this time onward each part of the system will
be depleted at an equal rate, thus the rate at which the pressure declines becomes the same
everywhere. For now, I’ll have to ask you to take this statement on faith. Later, after we have
developed the equations, we will see if we can prove that it is valid.
246
This type of flow is often called pseudosteady state, for, as we will see later, it has many
characteristics and equation forms similar to steady state flow. It has also occasionally been called
quasisteady state; however, this phrase never seemed to catch on in the petroleum industry. Dake,
in his book (1978) calls it semisteady state. This seems to be commonly used by the worldwide
Shell organization. I don’t like it because it is bad English; the prefix “semi” means “half,” which is
a meaningless term in this context. Craft and Hawkins (1959) on pp. 285-289 and others even refer
to this type of flow as “steady state.” This is clearly wrong. So I will use “pseudosteady state”
when discussing constant rate depletion of closed bounded systems. Let us turn now to
consideration of the implications of the depletion mechanism discussed earlier.
If we were to look at a given point in a reservoir, we can ask ourselves how much fluid is
flowing past that point. It seems clear that the fluid flowing past that point is only that fluid which
is being produced from points further out and which is flowing toward the well. At the outside edge
the flow is zero, as we move closer to the well the flow increases, and finally, as we get to the well,
the flow reaches the constant rate that was stipulated earlier.
These concepts can be put into equations, the forms of which will depend on the geometry
of the system. There are three geometries that are convenient to consider; linear, radial and
spherical. I’ll discuss all three, starting with the cylindrical (radial) system, for that is the one most
commonly seen in reservoir flow.
CYLINDRICAL (RADIAL) FLOW
Let us consider a closed cylindrical reservoir with a drainage radius,
r
e
, and a wellbore
radius,
r
w
. If the flow, q(
r
), at any distance,
r
, is proportional to the volume being depleted
beyond
r
, and the flow at the well, q
w
, is proportional to the entire drainage volume, we can
write the following equation:
q(r)
q
w
=
r
e
2
−r
2
r
e
2
−r
w
2
(1)
which is merely a mathematical statement of the idea. Note that Eq. 1 tells us that q(
r
) becomes
zero at
r
e
, and q
w
at
r
w
, as it should.
Let us now write Darcy’s Law for flow at any radius,
r
, and substitute Eq. 1 into it.
q(r) =−
2
π
khrdp
µ
dr
= q
w
r
e
2
−r
2
r
e
2
−r
w
2
(2a)
or, upon rearranging:
−
2
π
kh
q
w
µ
dp=
r
e
2
−r
2
r
e
2
−r
w
2
dr
r
(2b)
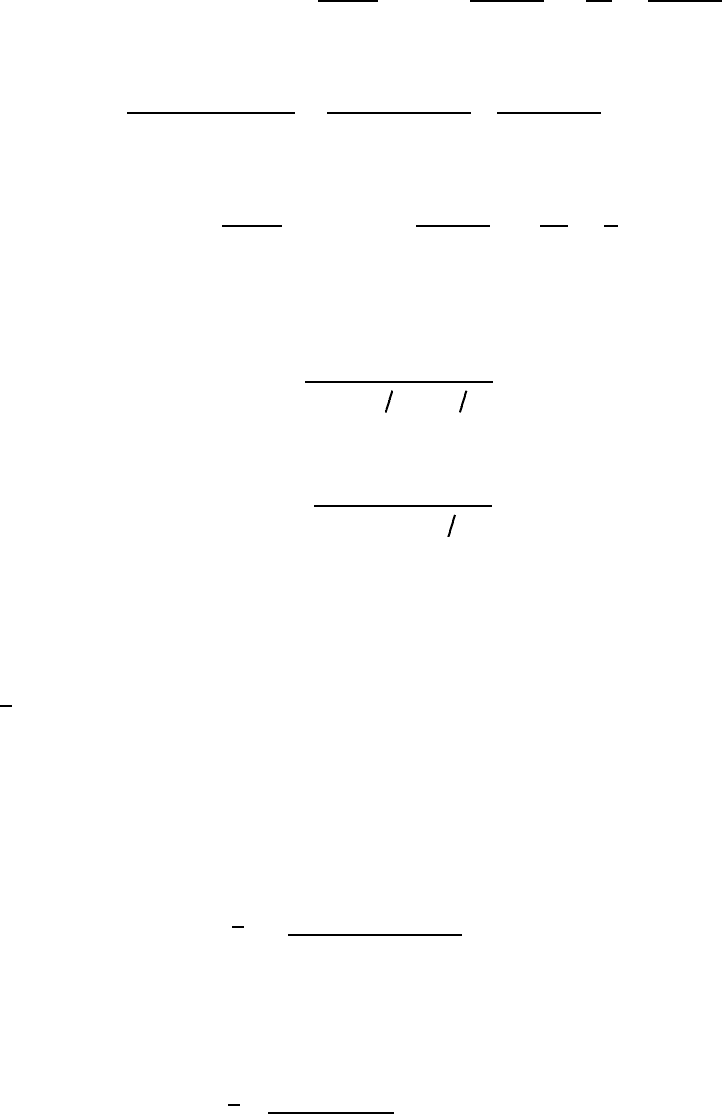
247
Let us integrate Eq. 2b from the wellbore out to a general radius,
r
, and also out to
r
e
:
−
2
π
kh
q
w
µ
p
w
p
(
r
)
∫
dp =
r
e
2
r
e
2
− r
w
2
dr
r
r
w
r
∫
−
1
r
e
2
−r
w
2
r
r
w
r
∫
dr
−
2
π
kh p(r)− p
w
[]
q
w
µ
=
r
e
2
lnr −lnr
w
()
r
e
2
−r
w
2
()
−
r
2
−r
w
2
()
2 r
e
2
−r
w
2
(
)
(3)
and, out to
r
e
:
−
2
π
kh
q
w
µ
p
e
− p
w
()=
r
e
2
r
e
2
−r
w
2
ln
r
e
r
w
−
1
2
(4)
In general, in reservoirs,
r
e
>>
r
w
; thus the ratio in front of the log term is nearly equal to 1.0, and
Eq. 4 can be simplified to:
q
w
=−
2
π
k
h
p
e
−
p
w
()
µ
ln r
e
r
w
()
−12
[]
or,
=−
2
π
k
h
p
e
−
p
w
()
µ
ln 0.607 r
e
r
w
()
(5)
A glance at either form of Eq. 5 will show why this type of flow is called pseudosteady state. The
equation certainly looks a great deal like the equation for steady state radial flow. It differs only by
the constant on the log term. Equation 5, however, is not very useful, for it contains the pressure
drop from the outer boundary to the well; and we seldom have a convenient way to measure that
outer boundary pressure. If we could, it would be much better to relate the equation to the average
pressure,
p
. This pressure could be measured easily in the field by merely shutting in the well and
allowing it to build up to its average pressure. Of course, transient testing pressure buildup
techniques could also be used to calculate this pressure.
The average pressure we want is the volumetric average. This means we need to integrate
pressure over the entire volume and divide it by the total volume, as follows:
p =−
r
w
r
e
∫
2
π
rh
φ
p(r)dr
r
w
r
e
∫
2
π
rh
φ
dr
or,
p =
r
w
r
e
∫
2rp(r)dr
r
e
2
−r
w
2
()
(6)
