Регеда В.В., Регеда О.Н. Основы алгоритмизации

Подождите немного. Документ загружается.

С помощью вложенных циклов выполняется и задача сортировки.

Сортировка – это расположение чисел в порядке возрастания или

убывания.

Наиболее распространенный и простой метод сортировки – метод

«пузырька». Он требует минимального объема памяти для данных,

но затраты времени на этот метод велики. Суть метода «пузырька» в

следующем. Пусть дано n чисел и необходимо расположить их (для

определенности) в порядке возрастания. При упорядочении можно

использовать следующий алгоритм:

1) числа сравниваются попарно: первое со вторым; второе с треть-

им; … , i-е с (i + 1)-м;

2) если меньшее стоит в паре на втором месте, то числа меняются

местами.

За один такой просмотр массива минимальное число перемещает-

ся по крайней мере на одно место вверх (вперед), а максимальное – в

самый конец, т. е. минимальное число как легкий пузырек воздуха в

жидкости постепенно «всплывает» в начало последовательности. От-

сюда название метода.

За K = (n

−

1) просмотров произойдет полное упорядочение масси-

ва при любом исходном расположении чисел в нем.

Рассмотрим алгоритм на примере шести чисел 2, 1, 4, 5, 6, 3

(n = 6).

2 1 4 5 6 3 – исходный массив

(Перестановка)

1 2 4 5 6 3 – после 1 шага

1 2 4 5 6 3 – после 2 шага

1 2 4 5 6 3 – после 3 шага

1 2 4 5 6 3 – после 4 шага

(Перестановка)

1 2 4 5 3 6 результат после 5 шага

Итак, после 5-го шага на последнем месте максимальное число «6»,

а минимальное число передвинулось на одно место вперед, и про-

изошли две перестановки. Если повторить указанный алгоритм еще

четыре раза (n – 2, где n – число элементов массива), то будет выпол-

нено полное упорядочение массива в порядке возрастания. На

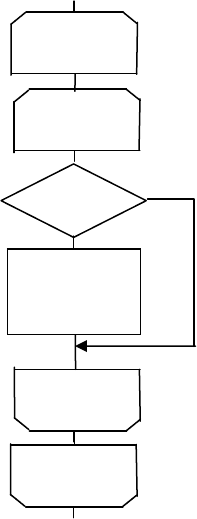
рис. 3.15 приведена соответствующая схема алгоритма.

Рис. 3.15

Глубину просмотра можно уменьшить, основываясь на том, что

большие числа «опускаются» вниз (в конец последовательности) и

затем не переставляются, поэтому их можно не анализировать при

последующих просмотрах.

При этом на схеме алгоритма конечное значение переменной

внутреннего цикла i должно зависеть от номера просмотра и рав-

няться n–K.

Сокращение количества просмотров улучшает временные характе-

ристики алгоритма. Этого можно достичь, проводя анализ того, были ли

K = 1, n

−

1, 1

i = 1, n

−

Нет

A(i)>A(i+1)

m = A(i + 1)

A(i + 1) = A(i)

A(i) = m

Да

перестановки на предыдущем просмотре. Если их не было, то можно

заканчивать сортировку – данные уже отсортированы. При большой

размеренности массивов это дает значительную экономию времени.

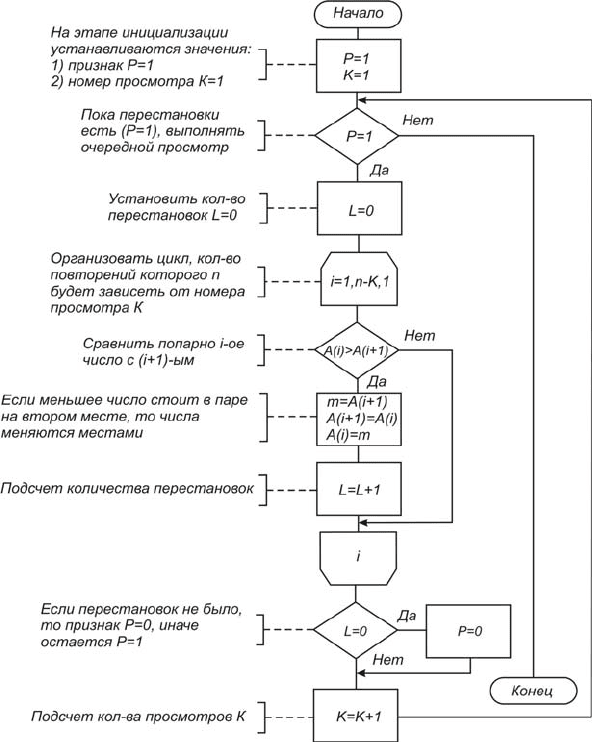
На рис. 3.16 приведен алгоритм, в котором для анализа наличия

перестановок при очередном просмотре введен признак: Р = 1 – пе-

рестановка есть; Р = 0 – перестановки нет.

Рис. 3.16

Двумерный массив, или матрица часто используется для описа-

ния данных одного типа. Например, таблицы сложения и умножения,

коэффициенты в системе линейных уравнений и т. п. Элементы мат-

рицы задают с помощью индексов: i – номер строки и j – номер

столбца

(1,1) (1, 2) . (1, )

(2,1) (2, 2) . (2, )

(, )

. ...

(,1) (,2) . (, )

AA Aj

А ij

Ai Ai Ai j

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

Для обработки массивов обычно образуют несколько вложенных

циклов. При этом в качестве переменной цикла будут выступать ин-

дексы матрицы. Для составления алгоритма необходимо определить,

как они меняются.

Рассмотрим фрагменты алгоритмов обработки массива.

Пример 10

Присвоить значения элементам матрицы А(5,3). Вычислить сумму

элементов заданной матрицы и вывести матрицу и полученную сум-

му на дисплей.

На рис. 3.17 приводится соответствующий алгоритм. После ввода

значения каждого элемента матрицы А(i, j) его значение выводится

на дисплей в строку и прибавляется к текущему значению перемен-

ной S. После завершения внутреннего цикла выполняется перевод

строки, алгоритм переходит на конец внешнего цикла и, пока i ≤ 5,

внутренний цикл снова повторяется, последовательно выводя все

пять строк матрицы. После выхода из внешнего цикла в переменной S

формируется искомая сумма, которая выводится на дисплей.

Пример 11

Ввести матрицу A(i, j) размерностью (i = 5, j = 8). Подсчитать ко-

личество отрицательных чисел в ней и заменить эти числа нулями.

Вывести новую матрицу. На рис. 3.18 приведен соответствующий

алгоритм.

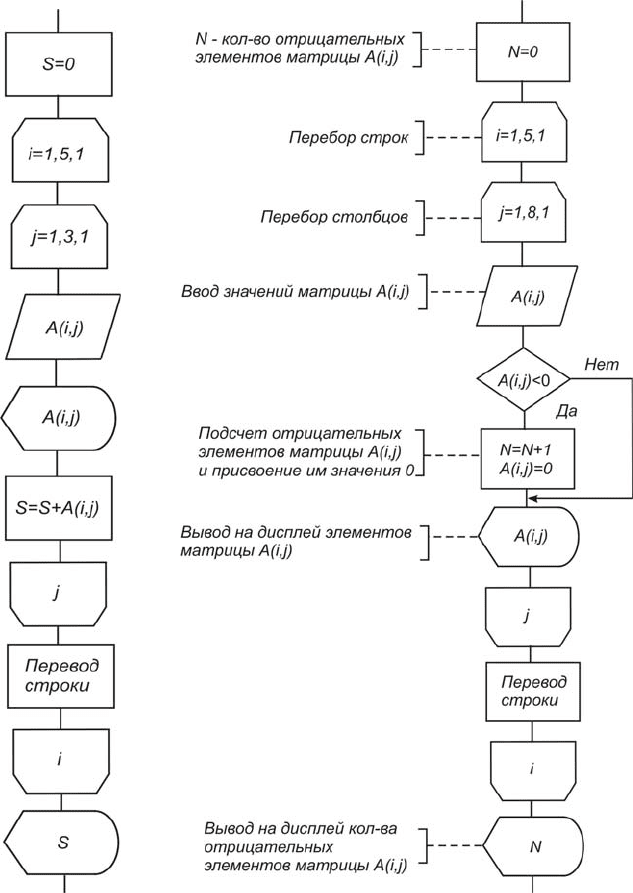
Рис. 3.17 Рис. 3.18

В данном алгоритме можно совместить в двух общих вложенных

циклах присвоение значений элементам матрицы, анализ их знака,

подсчет количества отрицательных элементов матрицы, их замену на

нуль и вывод матрицы.

Пример 12

Подсчитать и вывести на дисплей суммы элементов той же мат-

рицы по строкам. Схема алгоритма приведена на рис. 3.19.

Во внутреннем цикле для каждой строки матрицы формируются

промежуточные суммы элементов по строкам, а после выхода из

внутреннего цикла они выводятся на дисплей.

Прежде чем произойдет переход на следующую строку матри-

цы A(i, j), переменную S необходимо обнулить.

В некоторых случаях при обработке матриц достаточно организо-

вать только один цикл. Это, например, задачи, в которых обрабаты-

ваются диагонали матриц.

Пример 13

Для матрицы A(i, j) размерностью 8×8 подсчитать сумму элемен-

тов ее главной и побочной диагоналей и вывести их на дисплей.

При составлении схемы алгоритма (рис. 3.20) учтем, что элементы

главной диагонали имеют одинаковые индексы, а у побочной номер

строки и столбца связаны между собой следующим соотношением

j=9−i.

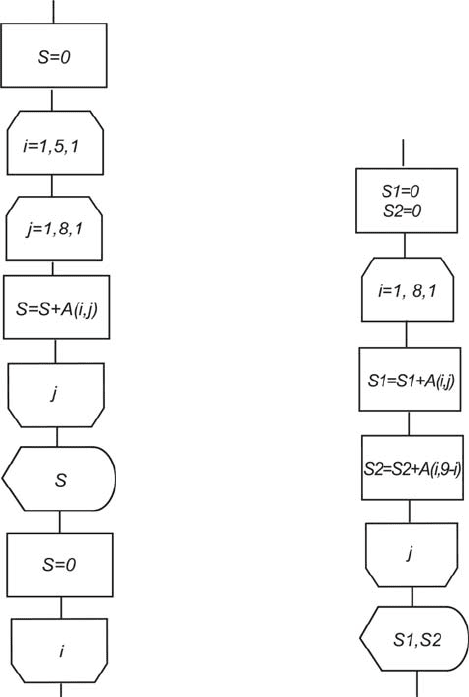
Рис. 3.19 Рис. 3.20

Задания для самостоятельного выполнения

1. Дана действительная матрица порядка M × N. Найти:

1.1. Сумму наибольших (наименьших) значений ее строк (столб-

цов).

1.2. Сумму элементов строки (столбца), в которой расположен

элемент с наименьшим (наибольшим) значением (предполагается,

что такой элемент единственный).

2. В данной действительной квадратной матрице порядка N × N:

2.1. Поменять местами строку, в которой расположен элемент с

наибольшим значением, со строкой, содержащей элемент с наи-

меньшим значением (предполагается, что такие элементы единст-

венны).

2.2. Указать индексы всех элементов с наибольшим (наименьшим)

значением.

2.3. Найти:

2.3.1. Строки (столбцы), элементы которых упорядочены по воз-

растанию (убыванию).

2.3.2. Сумму положительных (отрицательных) элементов на глав-

ной (побочной) диагонали.

2.3.3. Сумму элементов на обеих диагоналях.

2.3.4. Сумму положительных (отрицательных) элементов над/под

главной (побочной) диагональю.

2.3.5. Минимальный (максимальный) элемент на/над/под главной

(побочной) диагонали.

2.4. Для элементов главной диагонали, меньших/больших нуля,

вывести сумму/максимум/минимум элементов строки/столбца, где

этот элемент расположен.

2.5. Определить последовательность В(1)...В(N) из нулей и еди-

ниц, такую, что В(i) =1, если:

2.5.1. В строке/столбце матрицы есть хотя бы один отрицатель-

ный/положительный/нулевой элемент.

2.5.2. Строка/столбец образует возрастающую/убывающую по-

следовательность.

2.6. Вывести индексы ненулевых (или с другим признаком) эле-

ментов.

3. Транспонировать данную целочисленную квадратную матрицу

порядка 20×20.

4. Определить, является ли квадратная матрица симметричной от-

носительно главной (побочной) диагонали.

5. Даны две целочисленные квадратные матрицы порядка 20. Найти

по

мента i-й строки второй матрицы.

ых элементов i-й строки первой мат-

рицы той

в (некоторых переменных), участвующих в вы-

чи

ния

зад

а, т. е. не бу-

дет

тво состоит в том, что алгоритм должен

пр шению задачи за конечное число шагов.

о-

го

Пример 14

с п

−5

следовательность из нулей и единиц b

, …,b

, такую, что b

= 1, ко-

гда:

5.1. Все элементы i-х строк первой и второй матриц отрицательны.

5.2. Каждый элемент i-й строки первой матрицы больше соответ-

ствующего эле

5.3. Количество отрицательн

равно количеству отрицательных элементов же строки вто-

рой матрицы.

3.5. Итерационные циклы

Особенностью итерационного цикла является то, что число по-

вторений операторов тела цикла заранее неизвестно, а зависит от

значений параметро

слениях. Для его организации используется цикл типа «пока». Вы-

ход из итерационного цикла осуществляется в случае выполне

анного условия.

На каждом шаге вычислений происходят последовательное при-

ближение и проверка условия достижения искомого результата.

Алгоритм, в состав которого входит итерационный цикл, называ-

ется итерационным алгоритмом. Итерационные алгоритмы исполь-

зуются при реализации итерационных численных методов. В итера-

ционных алгоритмах необходимо обеспечить обязательное достиже-

ние условия выхода из цикла (сходимость итерационного процесса).

В противном случае произойдет зацикливание алгоритм

выполняться основное свойство алгоритма – результативность

(или конечность). Это свойс

иводить к ре

Рассмотрим применение итерационного метода для приближенн

вычисления функций.

Вычислить значение функции sin(Х) по приближенной формуле

F = sin

3 5

! − ... (Х) = X − X /3! + X / 5

огрешностью E=10 .

Функция F представляет с нов степенного ряда:

функции F

лен ряда; U – следующее слагаемое.

Запишем формулы для вычисления U учитывая, что в выраже-

нии для sin(Х) присутствуют только нечетные степени Х и факториа-

общий член ряда равен

обой сумму чле

F = U

+ U

+ ... + U

Условие окончания вычисления

– U

n+1

| ≤ E,

где U

– общий ч

n+1

Слагаемые можно определить:

1) непосредственно по формуле (но при большом значении n это

неэффективно);

2) используя предыдущее значение.

лы нечетных чисел. Если

(2 1)!

−

то следующее слагаемое

(2 1)!

=−

Откуда U

n+1

через U

можно определить как

2(2

−⋅

Рассмотрим сначала словесный алгоритм.

та X и точность вычисления Е.

, U

n+1

= Х .

= U

n+1

4. Вычислить F = F + U

5. Увеличить n = n + 2.

1. Ввести значения аргумен

2. Положить F = 0, n = 1

3. Заменить U

6. Вычисли ь

2(2 1)nn

−⋅

n+1

– U

| > E, повторять пункты 3−6.

7. Пока