Реферат - Автокорреляция уровней временного ряда и её последствия

Подождите немного. Документ загружается.

ОГЛАВЛЕНИЕ

I. ОПРЕДЕЛЕНИЕ АВТОКОРРЕЛЯЦИИ 3

II. АВТОКОРРЕЛЯЦИЯ УРОВНЕЙ ВРЕМЕННОГО РЯДА 5

III. ПОСЛЕДСТВИЯ АВТОКОРРЕЛЯЦИИ 13

СПИСОК ЛИТЕРАТУРЫ 14

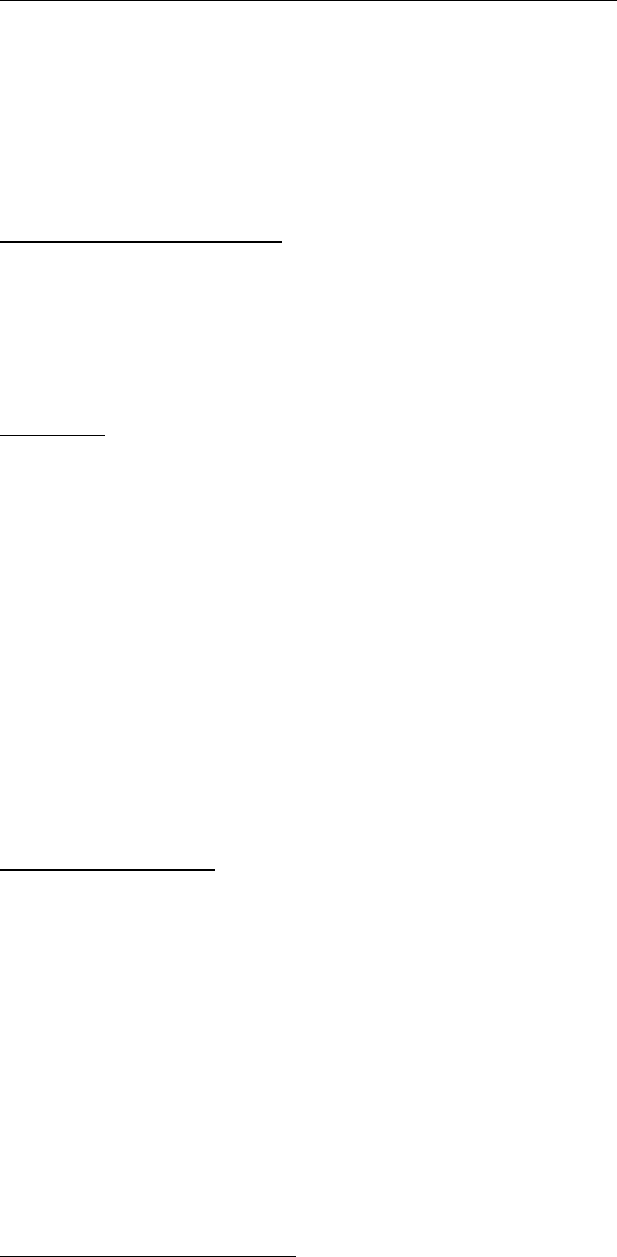
I. ОПРЕДЕЛЕНИЕ АВТОКОРРЕЛЯЦИИ

Автокорреляция (последовательная корреляция) определяется как

корреляция между ошибками в наблюдениях, упорядоченными во времени

(временные ряды) или в пространстве (пространственные данные).

Среди основных причин, вызывающих появление автокорреляции,

можно выделить следующие:

Ошибки спецификации. Отсутствие учета в модели какой-либо важной

объясняющей переменной либо неправильный выбор формы зависимости,

обычно приводит к системным отклонениям точек наблюдений от линии

регрессии, что может обусловить автокорреляцию.

Инерция. Многие экономические показатели (например, инфляция,

безработица, ВНП и т. п.) обладают определенной цикличностью, связанной

с волнообразностью деловой активности.

Действительно, экономический подъем приводит к росту занятости,

сокращению инфляции, увеличению ВНП и т.д. Этот рост продолжается до

тех пор, пока изменение конъюнктуры рынка и ряда экономических

характеристик не приведет к замедлению роста, затем остановке и движению

вспять рассматриваемых показателей. В любом случае эта трансформация

происходит не мгновенно, а обладает определенной инертностью.

Эффект паутины. Во многих производственных и других сферах

экономические показатели реагируют на изменение экономических условий с

запаздыванием (временным лагом). Например, предложение

сельскохозяйственной продукции реагирует на изменение цены с

запаздыванием (равным периоду созревания урожая). Большая цена

сельскохозяйственной продукции в прошедшем году вызовет (скорее всего)

ее перепроизводство в текущем году, а, следовательно, цена на эту

продукцию снизится и т.д.

Сглаживание данных. Зачастую данные по некоторому

продолжительному временному периоду получают усреднением данных по

составляющим его подынтервалам. Это может привести к определенному

сглаживанию колебаний, которые имелись внутри рассматриваемого

периода, что в свою очередь может послужить причиной автокорреляции.

I I. АВТОКОРРЕЛЯЦИЯ УРОВНЕЙ ВРЕМЕННОГО РЯДА

Обычно эконометрические модели строятся на основе двух типов исходных

данных:

 данные, характеризующие совокупность различных объектов в

определенный момент (период) времени;

 данные, характеризующие один объект за ряд последовательных

моментов (периодов) времени.

Модели, построенные по данным первого типа, называются

пространственными моделями. Модели, построенные на основе второго

типа данных, называются моделями временных рядов.

Временной ряд – совокупность значений какого-либо показателя за

несколько последовательных моментов или периодов времени. Каждый

уровень временного ряда формируется под воздействием большого числа

факторов, которые условно можно подразделить на три группы:

 факторы, формирующие тенденцию ряда (например, инфляция влияет

на увеличение размера средней заработной платы);

 факторы, формирующие циклические колебания ряда (например,

уровень безработицы в курортных городах в зимний период выше по

сравнению с летним);

 случайные факторы.

Очевидно, что реальные данные чаще всего содержат все три компоненты.

Модель, в которой временной ряд представлен как сумма перечисленных

компонент, называется аддитивной моделью временного ряда. Если же

временной ряд представлен как их произведение, то такая модель называется

мультипликативной.

Под временным рядом (time series) понимается последовательность

наблюдений значений некоторой переменной, произведенных через равные

промежутки времени. Если принять длину такого промежутка за единицу

времени (год, квартал, день и т.п.), то можно считать, что последовательные

наблюдения x1, ..., xn произведены в моменты

t = 1, …, n .

Основная отличительная особенность статистического анализа временных

рядов состоит в том, что последовательность наблюдений

x1, ..., xn рассматривается как реализация последовательности, вообще

говоря, статистически зависимых случайных величин X1, ..., Xn , имеющих

некоторое совместное распределение с функцией распределения

F(v1, v2, …, vn) = P{ X1 < v1, X2 < v2, ... , Xn < vn }.

Рассмотрим в основном временные ряды, у которых совместное

распределение случайных величин X1, ..., Xn имеет совместную плотность

распределения p( x1, x2, … , xn).

Чтобы сделать задачу статистического анализа временных рядов доступной

для практического решения, приходится так или иначе ограничивать класс

рассматриваемых моделей временных рядов, вводя те или иные

предположения относительно структуры ряда и структуры его

вероятностных характеристик. Одно из таких ограничений предполагает

стационарность временного ряда.

Ряд xt , t = 1, …, n , называется строго стационарным (или стационарным в

узком смысле), если для любого m ( m < n) совместное распределение

вероятностей случайных величин X t1…… X tm такое же, как и для X

t1+ш…… X tm + I , при любых t1,…, tm и I, таких, что 1 ≤ t1, … , tm ≤ n и 1

≤ t1+ д., … , tm+ I≤ n.

Другими словами, свойства строго стационарного временного ряда не

изменяются при изменении начала отсчета времени. В частности, при m = 1

из предположения о строгой стационарности временного ряда xt следует, что

закон распределения вероятностей случайной величины Xt не зависит от t, а

значит, не зависят от t и все его основные числовые характеристики (если,

конечно, они существуют), в том числе: математическое ожидание E (Xt) =

Mи дисперсия D(Xt)= Ớ2.

Значение М. определяет постоянный уровень, относительно которого

колеблется анализируемый временной ряд xt, а постоянная Ớ

характеризует размах этих колебаний.

Одно из главных отличий последовательности наблюдений,образующих

временной ряд, заключается в том, что члены временного ряда являются,

вообще говоря, статистически взаимозависимыми. Степень тесноты

статистической связи между случайными величинами Xt и Xt+ может

быть измерена парным коэффициентом корреляции

где

Если ряд xt стационарный, то значение не зависит от t и

является функцией только от ; мы будем использовать для него

обозначение :

В частности,

Соответственно, для стационарного ряда и значение коэффициента

корреляции

зависит только от ; мы будем использовать для него обозначение

так что

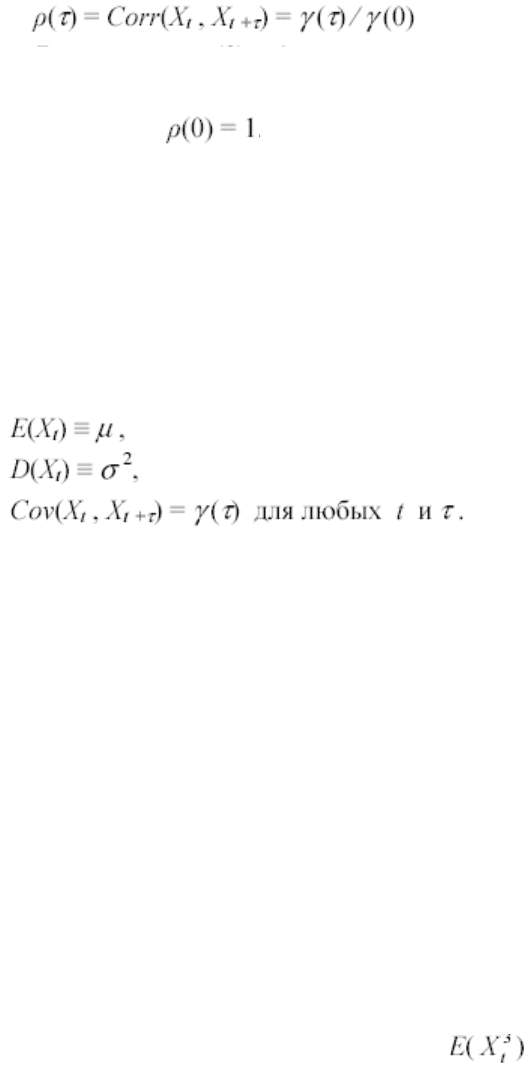
В частности,

Практическая проверка строгой стационарности ряда xt на основании

наблюдения значений x1, x2, …, xn в общем случае затруднительна. В связи с

этим под стационарным рядом на практике часто подразумевают временной

ряд xt , у которого

Ряд, для которого выполнены указанные три условия, называют

стационарным в широком смысле (слабо стационарным, стационарным

второго порядка или ковариационно стационарным).

Если ряд является стационарным в широком смысле, то он не обязательно

является строго стационарным. В то же время, и строго стационарный ряд

может не быть стационарным в широком смысле просто потому, что у него

могут не существовать математическое ожидание и/или дисперсия. (В

отношении последнего примером может служить случайная выборка из

распределения Коши.) Кроме того, возможны ситуации, когда указанные три

условия выполняются, но, например, зависит от t. Ряд xt , t = 1, …, n,

называется гауссовским, если совместное распределение случайных величин

X1, ... , Xn является n-мерным нормальным распределением. Для

гауссовского ряда понятия стационарности в узком и в широком смысле

совпадают.

В дальнейшем, говоря о стационарности некоторого ряда xt , мы (если не

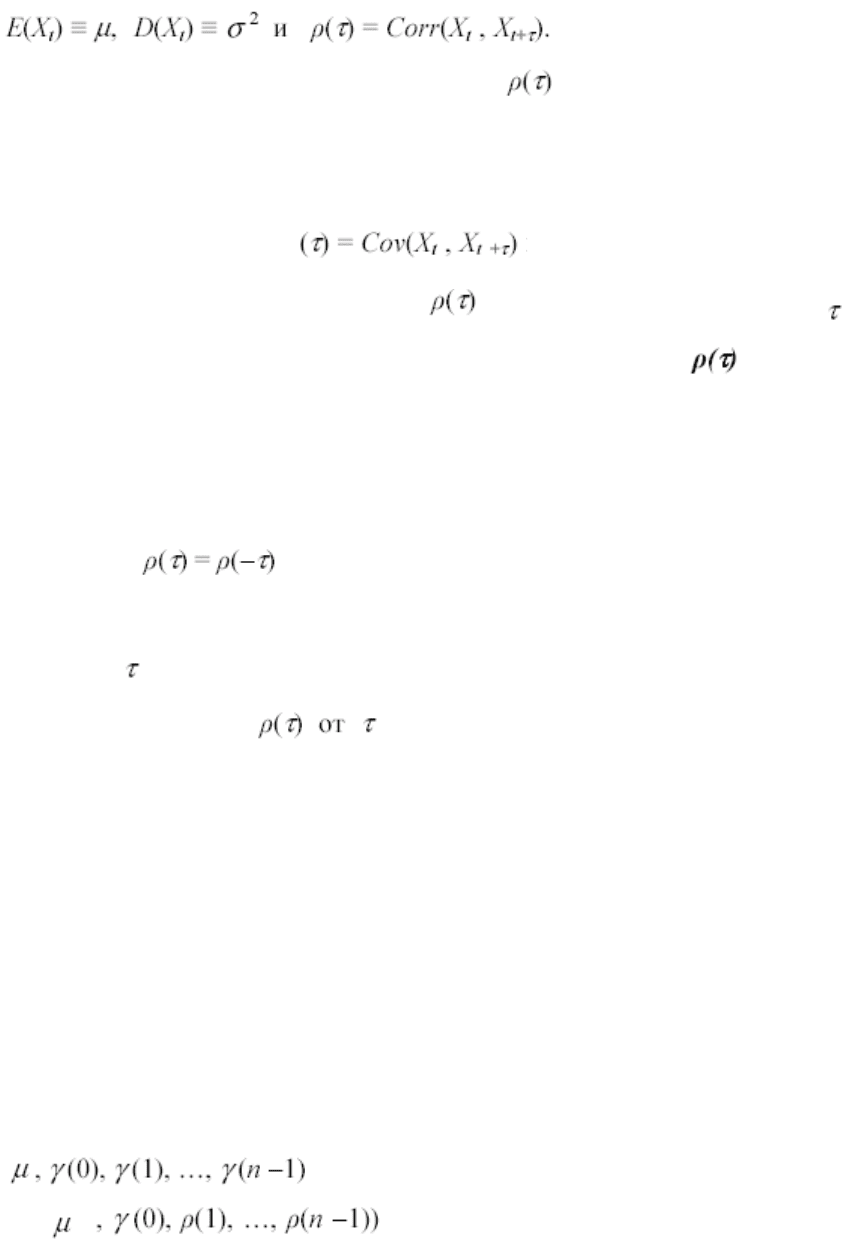
оговаривается противное) будем иметь в виду, что этот ряд стационарен в

широком смысле (так что у него существуют математическое ожидание и

дисперсия). Итак, пусть xt – стационарный ряд c

Поскольку в данном случае коэффициент измеряет корреляцию между

членами одного и того же временного ряда, его принято называть

коэффициентом автокорреляции (или просто автокорреляцией). По той же

причине о ковариациях говорят как об автоковариациях.

При анализе изменения величины в зависимости от значения

принято говорить об автокорреляционной функции .

Автокорреляционная функция безразмерна, т.е. не зависит от масштаба

измерения анализируемого временного ряда. Ее значения могут изменяться в

пределах от 1 до +1; при этом ρ(0) = 1. Кроме того, из стационарности ряда

xt следует, , так что при анализе поведения автокорреляционных

функций обычно ограничиваются рассмотрением только неотрицательных

значений .

График зависимости часто называют коррелограммой. Он может

использоваться для характеризации некоторых свойств механизма,

порождающего временной ряд. При этом заметим, что если

xt – стационарный временной ряд и

c – некоторая постоянная, то временные ряды

xt и (xt + c) имеют одинаковые коррелограммы.

Если предположить, что временной ряд описывается моделью стационарного

гауссовского процесса, то полное описание совместного распределения

случайных величин X 1, ..., X n требует задания n+1 параметров:

или

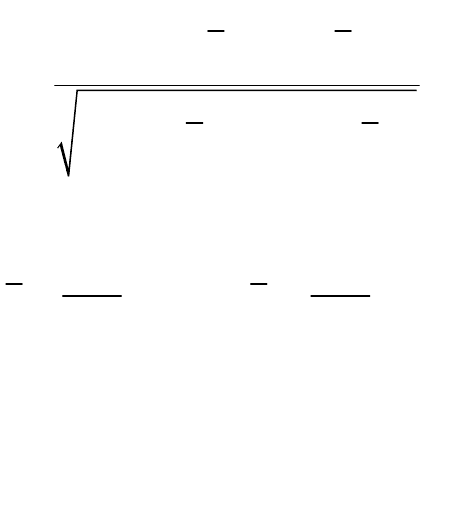
Это намного меньше, чем без требования стационарности, но все же больше,

чем количество наблюдений. В связи с этим, даже для стационарных

гауссовских временных рядов приходится производить дальнейшее

упрощение модели с тем, чтобы ограничить количество параметров,

подлежащих оцениванию по имеющимся наблюдениям. Мы переходим

теперь к рассмотрению некоторых простых по структуре временных рядов,

которые, в то же время, полезны для описания эволюции во времени многих

реальных экономических показателей.

При наличии во временном ряде тенденции и циклических колебаний

значения каждого последующего уровня ряда зависят от предыдущих.

Корреляционную зависимость между последовательными уровнями

временного ряда называют автокорреляцией уровней ряда.

Количественно ее можно измерить с помощью линейного коэффициента

корреляции между уровнями исходного временного ряда и уровнями этого

ряда, сдвинутыми на несколько шагов во времени.

Формула для расчета коэффициента автокорреляции имеет вид:

   

1 1 2

2 2

1 1 2

2 2

t t

n n

t t

y y y y







 

 



 



 

(4.1)

где

1 2 1

2 2

1 1

, .

1 1

n n

t t

y y y y

n n



 

 

 

Эту величину называют коэффициентом автокорреляции уровней ряда

первого порядка, так как он измеряет зависимость между соседними

уровнями ряда



Аналогично можно определить коэффициенты автокорреляции второго и

более высоких порядков. Так, коэффициент автокорреляции второго порядка

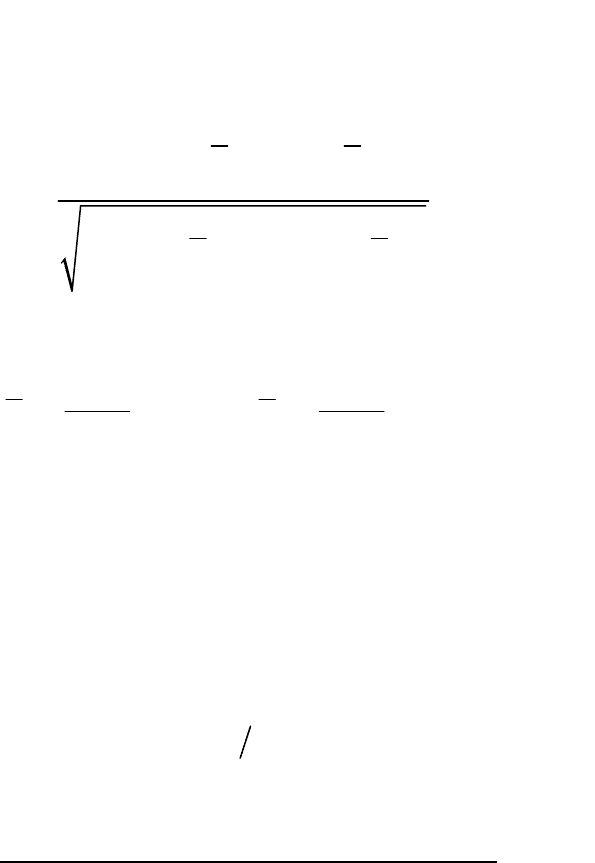
характеризует тесноту связи между уровнями



и определяется по

формуле:

   

3 2 4

2 2

3 2 4

3 3

t t

n n

t t

y y y y







 

 



 



 

(4.2)

где

3 4 2

3 3

1 1

, .

2 2

n n

t t

y y y y

n n



 

 

 

Число периодов, по которым рассчитывается коэффициент автокорреляции,

называют лагом. С увеличением лага число пар значений, по которым

рассчитывается коэффициент автокорреляции, уменьшается. Считается

целесообразным для обеспечения статистической достоверности

коэффициентов автокорреляции использовать правило – максимальный лаг

должен быть не больше

Свойства коэффициента автокорреляции.

Он строится по аналогии с линейным коэффициентом корреляции и

таким образом характеризует тесноту только линейной связи текущего и

предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции

можно судить о наличии линейной (или близкой к линейной) тенденции. Для

некоторых временных рядов, имеющих сильную нелинейную тенденцию

(например, параболу второго порядка или экспоненту), коэффициент

автокорреляции уровней исходного ряда может приближаться к нулю.

По знаку коэффициента автокорреляции нельзя делать вывод о

возрастающей или убывающей тенденции в уровнях ряда. Большинство

временных рядов экономических данных содержат положительную

автокорреляцию уровней, однако при этом могут иметь убывающую

тенденцию.