Рахман П.А. Основы защиты данных от разрушения. Коды Рида-Соломона
Подождите немного. Документ загружается.

РахманП.А., МЭИ(ТУ), 2007.
Основызащитыданныхотразрушения. КодыРида-Соломона.
Однаизнаиболееострыхпроблемвинформационныхтехнологиях– этозащита
данныхотразрушения. Какговорится, «энтропия»слепа, нотерпелива. «Энтропия» неимеет
собственной воли и неразрушаетцеленаправленноконкретный порядоквконкретной
структуре, ноунееестьединственнаяцель– глобальныйхаос, ионаслучайнымобразом,
вслепую, наносит свои удары по любым упорядоченным структурам, делая изних
бесформеннуюбессмыслицу. «Энтропия» вечна, фундаментальнаинепобедима. Скольконе
восстанавливайпорядок, онасноватерпеливостремитсявездедостичьбеспорядка. Чтобы
противостоять «энтропии» необходимо непрерывно затрачивать энергию, проявлять
изобретательностьиприменятьспециальныетехнологии.
Втечениебольшейчастивторойполовиныпрошлоговекаматематикииспециалисты
поаппаратным ипрограммным средствам ЭВМ ипроблемам передачиданныхупорно
билисьнадтем, чтобы выработатьтехнологию, позволяющую кодироватьинформацию
такимобразом, чтобы приразрушениислучайновыбранныхееблоков, этиблокиможно
быловосстановить. Послетого, какбылазаложенаматематическаяосновадлякодирования,
разработаныэффективныеалгоритмы кодированияидекодирования, технологияближек
концу прошлого векасталаболее или менееустоявшейся, и, честно говоря, вообще
превратиласьвширпотреб, которымпользуютсявсеповседневноидаженеподозреваютоее
существовании. Технологияприменяетсяприприеме/ передачеданныхвсетяхипричтении
/ записиданныхнабольшинственосителейинформации.
И здесь, еслипользователямидомохозяйкам можнопроститьихневежественно-
потребительскоеотношениеквысокимтехнологиям, тоужуважающиесебяспециалистыпо
системным и сетевым технологиям обязаны бытьзнакомы стонкостями и деталями
технологии. Ну, аужуважающиесебяпрограммисты, каквподтверждениесвоейвысокой
квалификации, должны иметь свои собственные корректно работающиепрограммные
реализациитехнепростыхалгоритмов, которыеиспользуютсявэтойтехнологии.
1. Краткооконечныхполях. ПоляГалуа.
Основнаятрудностьвпониманиитехнологиикодированиязаключаетсявтом, чтоона
базируетсянена привычной еще со школьной скамьи алгебре вбесконечном поле
вещественныхчисел, анаспециальнойалгебреконечныхполей[1], конкретнонаполях
Галуасколичествомэлементов, равным2
M
. ПолеГалуаобозначаетсяGF(2
M
). Аббревиатура
GF – этосокращениеотGalois Field. Какизвестно, впривычнойдлянасалгебреоперации
сложения/ вычитанияитемболееужумножения/ делениямогутдатьрезультат, который
выходитзапределынекоторогозаданногодиапазона. Например, еслимыимеемдиапазон
чиселот1 до100, иработаемтолькосчисламиизэтогодиапазона, то, например, результаты
операций: 45 + 90, 10 – 25, 50 * 30, 15 / 60 ужевыйдутзаэтотдиапазон. Авотвконечном
поле, любыеоперации слюбыми элементами этогополяврезультатедаютэлемент,
принадлежащийэтомужеполю. Соответственно, вконечныхполяхвообщеотсутствует
такиепроблемы, какпереполнениеприумноженииипотеряточностиприделении, делая
темсамымалгебруконечныхполейнаиболееестественнойсточкизренияЭВМ, которая
имеетконечнуюразряднуюсеткудляпредставленияданныхиконечнуюемкостьпамяти.
Впринципеалгебраконечныхполейнесложнее, аместамигораздодажепроще, чем
классическаяалгебра. Внейможновыполнятьлюбыеарифметическиеоперации, составлять
и решатьуравнения, и дажедифференцировать и интегрировать. Простыми словами,
конечное поле– это некоторая конечная совокупность чисел, над которыми можно
производитьчетыреарифметическиеоперации, невыходязапределыэтойсовокупности. В
частности, полеГалуаGF(2
8
), используемоевтехнологиикодирования, состоитиз2
8
= 256
целыхчиселот0 до2
8
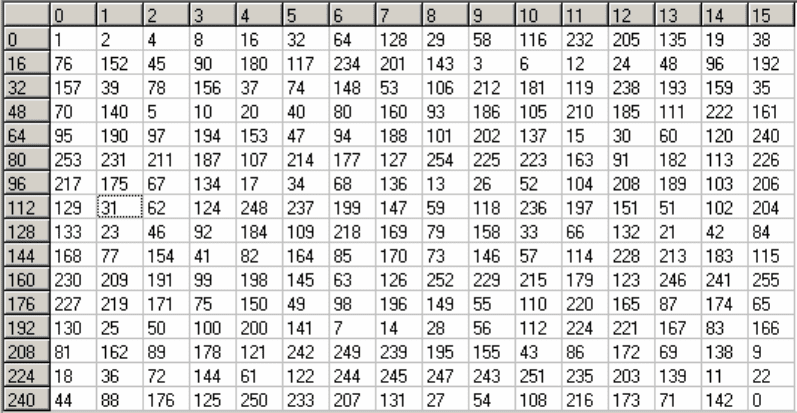
– 1, расположенныеневпорядкевозрастания, аособымобразом.
2
Согласнотеории, i-йэлементполяГалуа– эторезультатвозведениявi-ю степень
некоторогопримитивногоэлемента, вкачествекоторогообычноберетсяпростоечисло2,
гдеi = 0…2
8
– 1. Номысразувидим, что, уженачинаяi = 8, мыполучимрезультат, который
ужевыходитзапределы[0, 2
8
– 1] издесьиспользуетсяособыйподход.
Правилопервоначальнойгенерацииполятаково:
128]1[,285)1])1[(
128]1[),1]1[(
][
254...2
,0255,21,10
iGFiGF
iGFiGF
iGF
i
GFGFGF
Простымисловами, 0-йэлементполяэто1, 1-йэлемент– 2, а, начинаясо2-го
элементапо254-йэлемент, элементвычисляетсякакудвоенноезначениепредыдущего
элемента, иеслиудвоениепривелокчислу, вышедшемузаграницы8-разрядов, тонанего
делаетсяXOR счислом285
10
(11D
16
), наконец, последний255-йэлементполя– 0. Число285
– этодесятичноепредставление(11D вшестнадцатеричномпредставлении) такназываемого
неприводимогополиномаx
8
x
4
x
3
x
2
1, спомощью которогоипорождается
первоначальноеполе. Символом обозначаетсяоперацияXOR – побитовоесложениепо
модулю 2, асимволом<< обозначаетсялогическийсдвигвлеводвоичногопредставления
числанауказанноеколичестворазрядов, приэтомбиты, «вылезшиеслева» из8-разрядного
байта, пропадают, аразряды, «освобождающиесясправа», заполняютсянулями. Сдвигчисла
вдвоичномпредставлениинаодинразрядвлево– этоэквивалентноудвоениючисла.
Согласнотеории, сгенерированноеполеGF(2
8
), содержитрезультаты возведения
примитивногоэлемента«2» вовсестепени, начинаяс0, заканчивая255.
Помимо основного поляв технологии кодированиеважно также иметь и так
называемоеобратноеполе, позволяющеепозаданномузначению 2
k
выяснитьстепеньk, в
котороебыловозведенпримитивныйэлемент2, инымисловамииметьтаблицулогарифмов
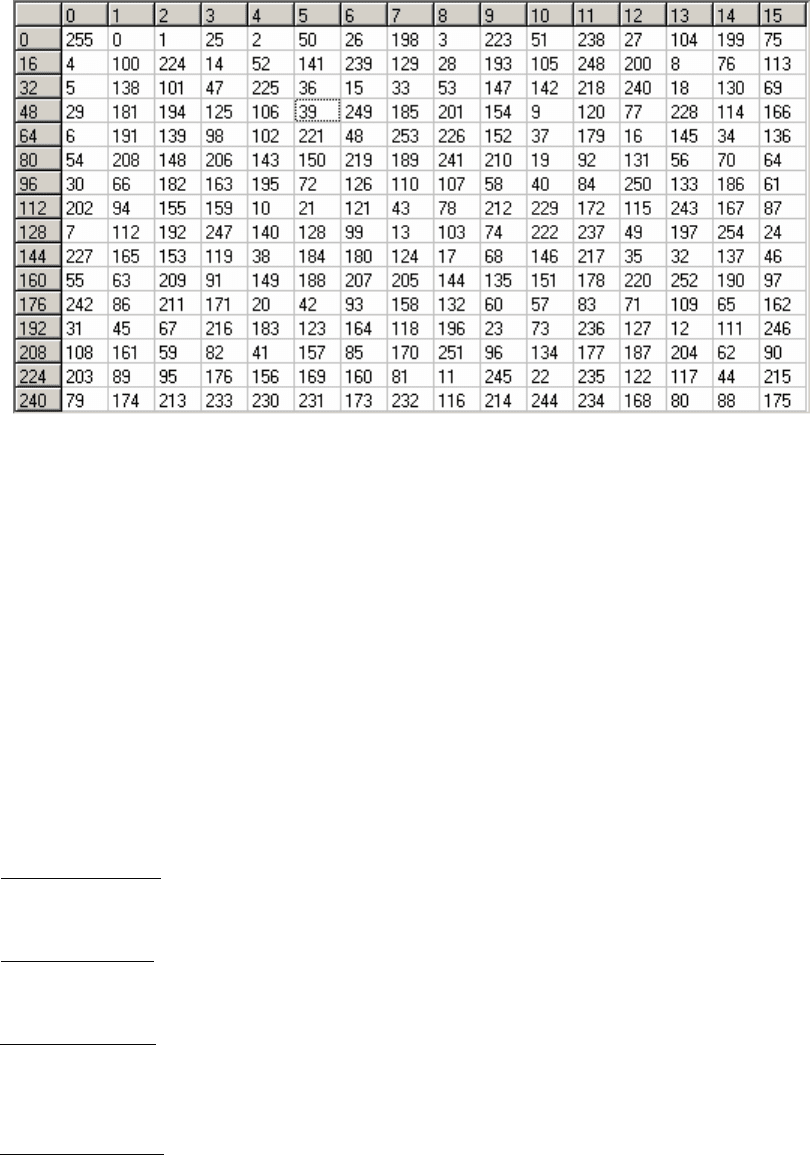
пооснованию2. Обратноеполевычисляетсядостаточнопросто:
iiGFGF
i
]][[
1
255...0
3
Согласнотеории, сгенерированноеобратноеполеGF
-1
(2
8
), содержитлогарифмывсех
элементов, начинаяс0, заканчивая255, пооснованиюпримитивногоэлемента2.
Такимобразом, используяэтидветаблицы, мы сводимоперациивычисления
i
2
и
)(
2
log i кпростомусчитыванию соответствующегоэлементаизосновногоилиобратного
поляГалуа. Вобычнойалгебревещественныхчиселотакойскоростиипростотевозведения
встепеньирасчеталогарифмадажеимечтатьнельзябыло.
Однако, мы ещенеопределили основныеарифметическиеоперации: сложение,
вычитание, умножениеиделение. Сосложениемивычитаниемэлементовполейвсепросто–
дляслучаяполяГалуаGF(2
8
) обеоперации считаютсяэквивалентными изаменяются
обычнойоперациейXOR – побитовоесложениепомодулю2.
Чтокасаетсяумноженияиделения, есливспомнитьшкольнуюалгебру, тологарифм
отпроизведениядвухчиселравнасуммелогарифмовоткаждогочиславотдельности, а
логарифм ототношения двух чисел равнаразности логарифмов откаждогочислав
отдельности. Тогдаоперацииумножения/ деленияможносвестиквычислениюлогарифмов
пооснованию2 отоперандов(пообратномуполюГалуа), сложению/ вычитаниюзначений
логарифмов, ивозведениечисла2 встепеньсуммы/ разности(поосновномуполюГалуа).
Примечание1. Длясложенияи вычитанияжестепеней используютсяобычные
правилаалгебры, операцияXOR здесьнедопустима. Еслисуммастепенейбольшеилиравна
255, тоизнеевычитается255. Еслиразностьстепенейменьше0, токнейприбавляется255.
Примечание2. Иногдатребуетсявычислитьпроизведениестепеней, вэтойситуации
такжеиспользуютумножениеизобычнойалгебры, однако, зарезультатберетсяостаток
произведенияпомодулю255.
Примечание3. Приоперацииумножения, еслиодинизоперандовравеннулю, то
сразувозвращаетсярезультат0. Иначевычисляютсялогарифмыотоперандов, ивычисляется
сумма. Еслисуммабольшелиборавна255, тоизсуммывычитается255. Послеэтогочисло2
возводитсяврезультирующуюстепень.
Примечание 4. При операции деления, если делитель равен нулю, то сразу
возвращаетсяошибка«делениянануль», аеслиделимоеравнонулю, ноделительнеравен
нулю, тосразувозвращается0. Иначевычисляютсялогарифмыотоперандов, ивычисляется
ихразность. Еслиразностьменьшенуля, токразностидобавляется255. Послеэтогочисло2
возводитсяврезультирующуюстепень.

4
Такимобразом, определим4 арифметическиеоперации:
)
8
2(,,
][
1
2
log
][2
0
255
2
log
2
log
20
2
log
2
log
2
log
2
log
20
2
log
2
log
0&0
00&0
/
255
2
log
2
log
2255
2
log
2
log
2
log
2
log
2255
2
log
2
log
0&0
00|0
GFxba
xGFx
xGF
x
Ошибкаb
ba
ba
ba
ba
ba
ba
ba
ba
ba
ba
ba
ba
ba
ba
baba
baba
Примечание1. ВполеГалуанетотрицательныхэлементов, операциисложенияи
вычитаниясведеныкоднойитойжеоперацииXOR. Еслиформальноговоритьо«замене
знака», то, воспользовавшисьправиломоперациивычитания, иположив 0
a , мыувидим,
что bb
. Положительныйэлементтождественноравенсебеотрицательному.
Примечание2. Вычислениеэлемента
1
b , приусловии 0
b и 1
b , сводитсяк
делениюэлемента
1
0
2
наb . Воспользовавшисьправиломделения, видим, что 01
2
log ,
0
2
log b , ихразностьменьшенуля, ирезультатравен
b
2
log255
2
. При 1
b , 1
1
b ,
при 0
b – ошибкаделениянануль.
Примечание3. Вычисление
uu
2/12
, приусловии 2550
u , учитывая, что
01
2
log и 02
2
log u
u
, ихразностьменьшенуля, сводитсяквычислению
u
255
2
.
При 0
u ,
1
2
u
. При 255
u степеньпредварительноберетсяпомодулю255.
Достаточнолегкоубедитсявнепротиворечивостиалгебрыконечногополя. Например,
еслисложить10 и15, получимрезультат10 XOR 15 = 5, теперьеслииз5 вычесть15,
получим5 XOR 15 = 10, такчтоусловиеa = (a + b) – b соблюдается. Или, например,
умножим7 на3, получим2 ^ (log
2
7 + log
2
3) = 2 ^ (198 + 25) = 2 ^ (223) = 9, теперьесли
разделить9 на3, получим 2 ^ (log
2
9 – log
2
3) = 2 ^ (223 – 25) = 2 ^ (198) = 7, такчто
соблюдаетсяусловие, a = (a / b) * b. Междупрочим, вслучаетрадиционнойалгебрывполе
вещественныхчисел, наЭВМ этоусловиенефактчтовыполнитсяточно, посколькупри
деленииможетпроизойтипотеряточности, иприпоследующемумножениичастногона
делительполучится неточно изначальноеделимое, а валгебреконечных полей все
абсолютноточно. Вообще, дляЭВМ вещественныечислаиоперациинаднимиглубоко
противоестественны, ЭВМ рожденадляработывконечныхполях.

5
2. Краткоополиномахиоперацияхнадними.
Такжекакивтрадиционнойалгебре, валгебреконечныхполей[1] можноговоритьо
функциях, представляемых в видестепенного ряда– иными словами, полиномах. В
частности, мыбудемрассматриватьфункцииоднойпеременной, причемсамапеременная
носитформальныйхарактер, исамапосебенеимееткакой-либосмысловойнагрузки. В
полиномеважны лишькоэффициенты, стоящиеприэтойпеременнойвсоответствующей
степениимыбудемкасатьсятолькослучая, когдаимиявляютсяэлементыполяГалуа.
10)
8
2(
1
0
0
1
1
1
1
k,iGF
i
A
k
i
i
x
i
AAxA
k
x
k
AxA
Примечание1. Особообратимвниманиенато, чтосамсимволсуммы, подразумевает
операциюсложенияпоправиламалгебрыполяГалуа, инымисловами, операциюXOR.
Примечание2. Припрограммнойреализацииполиномов, онипредставляютсяввиде
массивакоэффициентов, самажеформальнаяпеременная, иеестепенинигденехранятся.
«Степеньпеременной», при которойстоиткоэффициентоднозначно определяется, как
позиция(индекс) элементамассива, вкоторомхранитсякоэффициент.
Однаизнаиболееважныххарактеристикполинома– этоегостепень, определяемая
какнаивысшаястепеньпеременной, передкоторойстоитненулевойкоэффициент.
10
8
2
0:
10
maxdeg
k),iGF(
i
A
i
Ai
ki
xA
Над полиномамиможнопроизводитьарифметическиеоперации, такженаместо
формальнойпеременнойможноподставлятьконкретноезначение, являющеесяэлементом
поляГалуа, ивычислятьзначениефункции. Припересчетекоэффициентовполиномапри
выполненииоперациииливычислениизначениифункции, строгособлюдаютсяправила
арифметикидляполяГалуа. Основныеоперации, которыенампотребуютсявдальнейшем–
этосложение/ вычитаниеполиномов(внашемслучаеобеоперациисводятсякоперации
XOR), масштабированиеполинома, сдвигвлевонаоднупозицию, умножениеполиномови
вычисленияостаткаотделенияодногополиноманадругойполином.
Примечание3. Приперемноженииполиномов, очевидно, чтомассивкоэффициентов
результирующего полиномаимеетбольший размер, равный суммеразмеров массивов
коэффициентовперемножаемыхполиномов. Присдвигеполиномавлевонаоднупозицию,
массивкоэффициентоврезультирующегополиномаимеетразмернаединицубольше, чем
размермассивакоэффициентовисходногополинома.
Сложение/ вычитаниедвухполиномоввыполняетсяпутемвыполненияоперации
XOR длякоэффициентов, стоящихпередпеременнойводнойстепени. Отсутствующиев
полиномахкоэффициенты, разумеется, считаютсянулевыми.
10)
8
2(,
1
0
k,iGF
i
B
i
A
k
i
i
x
i
B
i
AxBxA
Масштабированиеполинома– умножениеполиноманаконстанту(являющуюся
элементомполяГалуа), котороесводитсякумножениювсехкоэффициентовэтогополинома
наконстантупоправиламполяГалуа.
10)
8
2(,
1
0
k,iGF
i
A
k
i
i
x
i
AxA
6
«Сдвигвлево» полиноманаоднупозицию эквивалентноумножениюполиномана
x, соответственно, при каждом коэффициенте степени переменной увеличивается на
единицу, сдругойточкизрения– коэффициенты«сдвигаются» наоднупозициювлево, ана
местомладшегокоэффициентаврезультирующемполиномезаписываетсянуль.
10,0
*
0
,
*
1
0
*
1
0
1
kiA
i
A
i
A
k
i
i
x
i
A
k
i
i
x
i
AxAx
Умножениедвухполиномовосуществляетсяпутемвычислениясуммырезультатов
произведенияодногополиноманакаждыйчлендругогополинома. Каждоепроизведение
сводитсякмасштабированиюодногополиномакаждымкоэффициентомдругогополиномаи
сдвигурезультирующегополиномавлевоначислопозиций, равномустепенипеременной,
прикоторойстоиткоэффициентвдругом полиноме, приэтомосвобождающиесясправа
позициизаполняютсянулями.
10,10)
8
2(,
2
0
10
10
1
0
1
0
ljk,iGF
j
B
i
A
lk
r
rji
lj
ki
j
B
i
A
r
x
k
i
l
j
j
x
j
B
i
x
i
AxBxA
Вычислениеостаткаотделенияодногополиноманадругойполином, илиболее
коротко– вычислениеостаткаодногополиномапомодулюдругого. Сделаемсразуоговорку,
что нам понадобитсятолько частный случай, когда старший коэффициентполинома
делителяравенединице, иэтосущественноупрощаетпроцедуруделения.
Пустьзаданполином-делимое )(xA степени 1
k , иполином-делитель )(xg степени
r
, причем 1
kr и 1
r
g . Делениеполиномовосуществляетсяпоправилам, похожимна
правила«делениявстолбик» втрадиционнойарифметике. Однако, естьиразличия.
Во-первых, вотличиеоттрадиционного деления, на каждом шагеделения «в
столбик» выполняется не вычитание, а операция XOR между соответствующими
коэффициентамисоответствующихполиномов, онихпойдетречьниже. Приэтомнакаждом
шаге rks
1 получается остаток )(
)(
x
s
R , который всегда состоит строго из
r
коэффициентов(столько же, сколько вделителе), старшиекоэффициенты могутбыть
нулевыми, и, темнеменее, эти«нулислева» никогданеотбрасываютсяиявляютсячастью
остатка. Изначально, за«начальныйостаток»принимаетсяследующийполином:
rj
rj
jrk
A
j
R
,0
10,
)0(
Во-вторых, при традиционном делении, на очередном шаге
s
остаток может
получатьсяразнойдлины (сразным количеством цифр), ивзависимостиотситуации,
«сверхуспускаются» необходимоеколичествоцифрделимоготак, чтобысформированное
таким образом число было больше либо равно делителя. Если «сверху спускается»
количествоцифр 1
w , товчастном справадописывают 1
w нулей. Приделенииже
полиномов«сверхуспускается» всегдатолькоодиночередной коэффициент
srk
A
делимогополинома )(xA , насоответствующемшаге ],1[ rks
.
7
В-третьих, вотличиеоттрадиционногоделения, «спущенныйсверху» коэффициент
srk
A
недописываетсясправа, аделаетсяпо-другому: остаток )(
)(
x
s
R , полученныйна
предыдущем шаге, сдвигаетсянаоднупозицию влево, анаместо младшей позиции,
записываетсяэтоткоэффициент.
0,
1,
)1(
1
)(*
j
srk
A
rj
s
j
R
s
j
R
Очевидно, при этом старший коэффициент
)1(
s
r
R старого полинома-остатка
пропадает, новэтомбеды нет, таккакнакаждомшаге ],1[ rks
деленияполучается
остаток, укоторогостаршийкоэффициентравеннулю, 0
)(
s
r
R , этобудетпоказанониже.
Крометого, какбылопоказаноранее, в«начальномостатке» также 0
)0(
r
R .
В-четвертых, притрадиционномделении, накаждомшагепослеприсоединенияк
очередномуостаткунеобходимогоколичествацифр, «спущенныхсверху» отделимого,
подбираетсяочереднаяцифрачастноготак, чтобыделитель, умноженныйнаэтуцифру, при
еговычитанииизсформированноговышечисладавалнеотрицательную разность, причем
меньшую, чем сам делитель. В случаежеделенияполиномов, очереднойкоэффициент
частного
)(s
Q выбирается так, чтобы старший коэффициент
r
g полинома-делителя,
умноженногонакоэффициентчастного(масштабированногокоэффициентомчастного), был
равенстаршемукоэффициентуполинома
)(* s
r
R , являющегосярезультатомсдвигавлевона
одну позицию остатка, полученного на предыдущем шаге. Иными словами, чтобы
соблюдалось
)(*)( s
r
R
r
g
s
Q . Учитываято, 1
r
g , нетруднозаметить, чтообеспечитьэто
условиедостаточнопросто, сделав«обратную связь», покоторой передаетсястарший
коэффициентполинома, являющегосярезультатомсдвигавлевонаоднупозицию остатка,
полученногонапредыдущемшаге, иименноонпринимаетсязаочереднойкоэффициент
частного. Инымисловами,
)1(
1
)(*)(
s
r
R
s
r
R
s
Q .
Послеэтого, остатокнатекущемшаге rks
1 вычисляетсякак:
rj
s
r
R
j
g
s
j
R
s
j
R 0,
)(*)(*)(
Учитывая, что 1
r
g , заметим, что 0
)(*)(*)(
s
r
R
s
r
R
s
r
R . Тогда, окончательно
получаемрекуррентноесоотношениедлявычисленияостатканашаге rks
1 :
0,
)1(
10
1,
)1(
1
)1(
1
)(
j
s
r
Rg
srk
A
rj
s
r
R
j
g
s
j
R
s
j
R
Тогдапослевыполненияпоследнегошага rks
, мыбудемиметьискомыйостаток
отделенияполинома )(xA наполином )(xg : )(
)(
)(mod)( x
rk
RxgxA
.
Заметим, чтостарший
й
r
коэффициентполинома-остаткабудетвсегдаравеннулю,
и фактическая степень полинома-остатка 1)(deg
rxR , поэтому именно полином
)(
0
)(
1
1
)(
1
rk
Rx
rk
R
r
x
rk
r
R
ипринимаетсязаостаток.

8
Пример1. Вычислимостатокполинома
00
2
51
3
50
4
49 xxxxxA по
модулюполинома
86
2
xxxg .
249148
2
49)(
86
2
)(
155248
2
0)(
15544
2
249
0
0212
2
249
212
2
249
3
0
212
2
95
3
148
1
0
2
166
3
148
2
166
3
148
4
0
2
149
3
166
4
49
2
2
51
3
50
4
49
3
3
50
4
4
49
5
0
)0(
xxxQ
xxxg
xxxR
xx
A
xx
xxx
xxx
x
A
xx
xxx
xxx
x
A
xx
x
A
x
A
x(x)R
Врезультатеполучаемостаток:
155248 xxR .
Пример 2. Проверим корректность операции деления в предыдущем примере,
вычислив выражение )()()( xRxgxQ
. Сложив произведение частного и делителя с
остатком, мыдолжнысноваполучитьисходноеделимое.
2
51
3
50
4
49155248155248
2
51
3
50
4
49
155248
824962498148
2
12496148849
3
1148649
4
149
15524886
2
249148
2
49)()()(
xxxxxxxx
x
xxxx
xxxxxxRxgxQ
Видим, что
2
51
3
50
4
49)()()( xxxxRxgxQ нечтоиное, какисходный
полином-делимое
xA впредыдущемпримере. Этоподтверждаеткорректностьпроцедуры
вычисленияостаткаодногополиномапомодулюдругогополинома.
9
Нетруднозаметить, чтокакврекуррентномсоотношениидлявычисленияостаткана
шаге rks
1 , так и в приведенном примере, явно видно, что на каждом шаге
вычисляетсястаршийкоэффициентостатка
)(s
r
R , который, во-первых, нигдепотом не
используется, авовторых, послекаждогошагастановитсянулевым. Издесь, еслимыдля
большейнаглядностиоперацииделения«держалидлясвоихнужд» этоткоэффициент, тов
практическойреализации, очевидно, делатьподобноесовершенноизбыточно.
Чтокасаетсяочередногокоэффициентачастного, тоегоможновзятьизостатка,
вычисленногонапредыдущемшаге
)1(
1
)(
s
r
R
s
Q , инымисловами, взятьпредпоследний
йr
)1( коэффициент остатка, полученного напредыдущем шаге, до того как мы
выполнимегосдвигнатекущемшаге. Тогдасучетомсказанного, окончательнополучаем
математическуюмодельпроцедурывычисленияостаткаполинома
xA помодулю )(xg :
rks
j
s
r
Rg
srk
A
rj
s
r
R
j
g
s
j
R
s
j
R
rj
jrk
A
j
R
1
0,
)1(
10
11,
)1(
1
)1(
1
)(
10,
)0(
Следует отметить, что процедура фактически сводится к последовательности
операцийсдвига, скажемтак, некоторого
r
разрядногорегистра(внашемслучаеразряд–
этонеодинбит, ацелыйбайт– 8-битноечисло), хранящегоостаток
)1(
0
)1(
1
s
R
s
r
R ,
полученныйнапредыдущемшаге, исложенияегос
r
разряднымделителем(безстаршего
коэффициента 1
r
g ), умноженногонастаршийкоэффициентостатка
)1(
1
s
r
R . Присдвиге
регистраостаткавегомладший й
0 разрядзагружаетсяочередной, коэффициент
srk
A
полинома-делимого. Перед началом процедуры, в регистр остатка загружаются
коэффициенты
rk
A
k
A
1
исходного полинома. Подобная схема легко реализуется
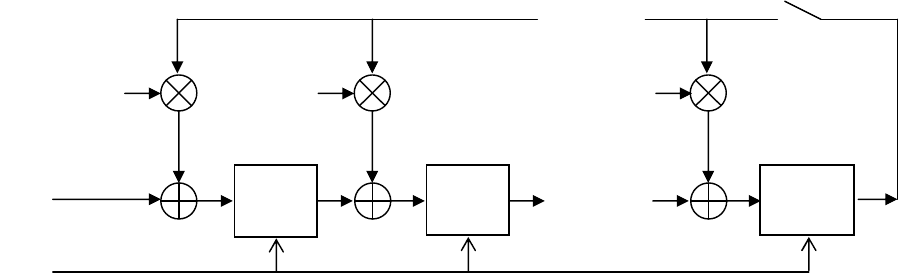
аппаратноввидесдвиговогорегистрасобратнойсвязью.
Вприведеннойнижесхеме, напервойфазе, ключобратнойсвязиSwitch разомкнути
в течение
r
тактов в регистре остатка загрузятся коэффициенты
rk
A
k
A
1
,
поступающиечерезмладший разряд регистра. Посколькуключ разомкнут, на схемах
сложенияонибудутскладыватьсяснулем, ипоступятврегистрвисходномвиде. Вовторой
фазе, ключ(Switch) замкнут, ивтечение rk
тактовбудетвычисленостаток. Искомый
остатокможнобудетсчитатьизрегистрапослепоследнеготакта. CLK – входдлятактовых
сигналов, понему«разряды» регистрапринимаютинформациюсосвоеговхода.
)(
0
s
R
)(
1
s
R
)(
1
s
r
R
10 k
AA
1
g
0
g
1
r
g
Switch
…
…
CLK

10
3. Введениевтеорию кодирования. КодыРида-Соломона.
Мы незрястольподробнорассматриваликонечныеполя, конкретнополеГалуа
GF(2
8
), иправилаарифметикивних, атакжеполиномыиоперациинаднимивполеГалуа,
посколькутехнологиякодированияидекодированиясприменениемтакназываемыхкодов
Рида-Соломона[2, 5, 6, 7] опираетсяименнонаних.
Идеяпредельнопроста, вЭВМ основнойединицейинформацииявляетсябайт, в
которомможетбытьзакодированоодноиз256 значений, именноэтоиобусловливаетвыбор
некакого-либо конечного поля, аименнополяГалуа GF(2
8
), котороесодержит256
различныхэлементов. Любоеинформационноесообщениеилиблокданныхмогутбыть
рассмотрены, как последовательности байтов. Более того, можно ввести формальную
переменную
x
итогдаэтибайты могутрассматриватьсякаккоэффициенты полинома,
причем, очевидно, чтостепеньполиноманаединицуменьшедлинысообщения.
Инымисловами, пустьимеетсянекотороесообщение, состоящееизk байтов.
Тогдамыможемеготакжепредставитьввидеполиномастепениk – 1:
10)2(
1
0
0
1
1
1
1
8
k,iGF
i
M
k
i
i
x
i
MMxM
k
x
k
MxM
Соднойстороныкаждыйбайтсообщенияможетсодержатьлюбоеиз256 возможных
значений, сдругойстороныполеГалуаGF(2
8
) такжесодержитвсевозможные256 различных
элемента, такчтоникакихпроблемневозникает. Простовполиномиальномпредставлении
«байты» сообщения уже являются не просто «байтами», они также трактуются как
коэффициентыполинома, являющиесяэлементамиполяГалуаGF(2
8
).
Важнымпонятиемвтеориикодирования[5] является, кодовоерасстояние. Пусть
заданыдвасообщения
A
и
B
одинаковойдлины k . Упрощенно, кодовоерасстояние– это
число байтов, которое у них отличаются значениями в соответствующих позициях.
Например, кодовоерасстояниемеждутекстовымисообщениямиABCDE иAFGDE равно2.
КодовоерасстояниемеждусообщениямиABCDE иACBDE такжебудетравно2, поскольку
имеетсянесовпадениевдвухпозициях, несмотрянато, чтовобоихсообщенияхучаствуют
символыизодногоитогоженабора. Болеестрогодатьопределениекодовогорасстояния
можно, еслипредставитьсообщенияввидеполиномов.
Пустьзаданы двасообщения
A
и
B
одинаковойдлины k , которыемогутбыть
представлены соответствующими полиномами
0
1
1
1
1
AxA
k
x
k
AxA
и
0
1
1
1
1
BxB
k
x
k
BxB
. Тогда кодовое расстояние
BAD , между этими
сообщенияопределяетсякак:
0,1
0,0
1
0
,
j
B
j
A
j
B
j
A
j
k
j
j
BAD
Всевозможныевариантыразличныхсообщенийдлины k образуют, такназываемое,
k -мерноепространство сообщений. Очевидно, чторазличныесообщенияпространства
могутотличатьсядруготдругавколичествепозицийот1 доk , инымисловамикодовое
расстояниемеждуразличнымисообщениямипространстванаходитсявпределах: kD
1 .
M
k – 1
… M
0
M
1
