Рахман П.А. Основы защиты данных от разрушения. Коды Рида-Соломона
Подождите немного. Документ загружается.

11
В теории кодирования исключительно важной характеристикой пространства
сообщенийявляетсяминимальноекодовоерасстояниеd , инымисловами, наименьшее
количествопозиций вкоторыхмогутразличатьсядваразныхсообщенияиззаданного
пространства. Внашемслучаеэтавеличинаравнаединице, посколькудваразныхсообщения
отличаются, какминимум, воднойпозиции, иначеонипростосовпадают.
1,
255,,0
,
min
BAD
Z
k
ZBA
d
Чтоещеболееважно– любоесообщение, принадлежащееk -мерномупространству
сообщений, является, так сказать, «легальным», «допустимым», имеющим право на
существование. Действительно, намможетпонадобитьсяпредставитьвсообщениисамые
разныекомбинациизначенийбайтов, длякодированияпроизвольныхвидовинформациии
мынеможемнакладыватьздесьникакихограничений. Именноэтопрепятствуетнамкаким-
либообразомобнаруживатьи, темболееуж, исправлятьискаженныесообщения.
Чтобы появиласьвозможностьобнаружения(атакже, частично, иисправления)
искаженийвсообщениях, согласнотеориикодированиятребуетсярасширитьпространство
сообщений, путем увеличения длины сообщений за счет введения, так называемых,
избыточныхсимволов: внашем случае– избыточныхбайтов. Номалопростоввести
избыточные байты, необходимо также расширенное пространство сообщений строго
поделитьнаподпространство«допустимых» («легальных») сообщенийиподпространство
«недопустимых» («нелегальных») сообщений. Тольковэтомслучаеунасбудетвозможность
приприемеилисчитываниисообщения, выявить«допустимость» сообщения. Очевидно
также, чтозначенияизбыточныхбайтов, должны как-тобытьсвязаны созначениями
информационныхбайтов, анебытьпроизвольными, посколькувтакомслучаемыбудем
иметьвсеголишьрасширенноепространство, вкоторомвсесообщения«допустимы».
Пусть задано исходное k -мерное пространство информационных сообщений
(множествовсевозможныхвариантовинформационныхсообщенийдлиныk ). Расширимэто
пространствопутем введенияизбыточных
r
байтовдо rkn
-мерногопространства,
причемпредъявимследующееключевоетребование:
r
избыточныхбайтовдолжнызависеть
от k информационныхбайтовтаким образом, чтобы минимальноекодовоерасстояние
подпространства «допустимых» сообщений было 1
rd . Иными словами чтобы
«допустимые» сообщения, вместе с корректно вычисленными для них значениями
избыточныхбайтов, отличалисьдруготдруганеменеечемв 1
rd позициях.
Вэтомслучаесогласнотеориикодированияприприемеилисчитываниисообщения
мысможемобнаруживатьискажениесообщения, вплотьдов
r
позициях. Болеетого, теория
кодированияутверждает, чтоможнотакжеобеспечитьгарантированноеисправлениеошибок
при искажениях вплоть до в
2/r позициях. Мы небудем излагатьздесьстрогих
доказательствэтих утверждений. Интуитивно понятно, чтомы можем гарантированно
обнаружить искажение, только если сообщение
*
M
«отклонилось» от исходного
«допустимого» сообщения
M
накодовоерасстояниеменеечемd , т.е. ( dMMD ),
*
( ). При
отклонении уже на расстояние d сообщение может попросту совпасть с другим
«допустимым» сообщениемиошибканебудетобнаружена. Чтожекасаетсявозможности
исправления, мы гарантированноможемисправитьошибки, толькоеслисообщение
*
M
«отклонилось» от исходного «допустимого» сообщения
M
менее чем половину
минимального кодового расстояния 2/),
*
( dMMD , и в этом случае мы можем
«притянуть» обратно искаженноесообщениекего исходному«допустимому» виду. В
противномслучае, еслисообщение«отклонилось» наполовинуилибольшеерасстояниеот
исходного сообщения, то оно уже«ближе» к другому «допустимому» сообщению и
корректноеисправление(восстановлениеисходногосообщения) невозможно.

12
Обозначим, через
t
- максимальную кратность исправляемой ошибки, иными
словами, предельное число искажаемых байтов, при котором еще возможно их
гарантированноеисправление. Учитываяпредыдущиерассуждения, несложнозаметить, что
этотпараметроднозначносвязанстребованиемкминимальномукодовомурасстоянию и
требуемымколичествомизбыточныхбайтов. Длятого, чтобыисправлятьошибкивплотьдо
t
-кратных, минимальноекодовоерасстояниеподпространства«допустимых» сообщений
должно быть, как минимум, быть больше чем удвоенная максимальная кратность
исправляемыхошибок, иными словами, td 2
. Какминимум, мы должны обеспечить
минимальноекодовоерасстояние, хотыбы наединицубольше, удвоенноймаксимальной
кратностиисправляемойошибки, инымисловами 12
td . Тогда, учитываячто 1
rd ,
нампонадобятся tr 2
избыточныхбайтов, чтобы обеспечитьминимальноетребование.
Заметимтакже, изприведенныхвышерассужденийследует, чтопритакомминимальном
кодовомрасстояниивозможнообнаружениеошибоквплотьдо trd 21
кратных.
Такимобразом, пустьзаданопространствосообщенийдлиныk . Тогда, введя, tr 2
избыточных байтов, то есть, расширивпространстводо rkn
-мерного, и наложив
главноетребованиеотом, чтоподпространство«допустимых» сообщенийдолжнообладать
минимальнымкодовымрасстоянием 121
trd , мы обеспечимобнаружениеошибок
кратностивплотьдо t2 , иисправлениеошибок, вплотьдократности
t
. Требованиевполне
логичноеивыполнимое. Мы имели пространствосообщений длины k , дляхранения
которыхтребовалосьk байт, которыеотличалисьвхудшемслучаетольководномбайте.
Потом же, «пожертвовав» избыточными tr 2
байтами, для хранения избыточной
информации, котораядолжнаоднозначновычислятьсяизисходной«полезной» информации,
хотимполучитьподпространство«допустимых» сообщенийдлины rkn
, которыебудут
отличатьсявхудшемслучаенеменее, чем 121
trd байтами.
Ключевойвопросвтом, какжеименновычислятьизбыточныебайты, такчтобыс
помощьюнихлюбоесообщениедлиныk исходногопространствасминимальнымкодовым
расстоянием 1
d , можно было преобразовать в сообщение длины rkn
подпространствасминимальнымкодовымрасстоянием 1
rd .
Теория кодирования предлагает следующий подход с использованием, так
называемыхкодовРида-Соломона, определенныхвконечномполеГалуаGF(2
8
). Вводится
понятие, такназываемогопорождающегополинома:
)2(2
2
1
2
8
GF
t
i
i
xxg
Порождающийполиномсогласнотеориикодированияиобеспечивает«генерацию»
tr 2
избыточныхбайтовизk байтовисходногосообщения(причемлюбого), такчтобы
результирующее«расширенное» сообщение, состоящееиз rkn
байтов, получающеесяв
результатесоединениябайтовисходногосообщениясизбыточнымибайтами, принадлежало
rkn
-мерному подпространству с минимальным кодовым расстоянием 1
rd .
Нетруднозаметить, чтопорождающий полином имеетстепень tr 2
, и егокорнями
являются элементы поля Галуа GF(2
8
), соответствующие результатам возведения
примитивногоэлемента2 встепени t22,1 , инымисловами, элементы:
t2
2,
2
2,
1
2 .
Примечание. Вычислимдляпримера, порождающийполиномдляслучаяпостроения
кодасвозможностьюисправленияодиночныхошибокислучаяошибокдвойнойкратности:
1
t :
86
2
2
1
2
xx
i
i
xxg
:2
t
116231
2
216
3
30
4
4
1
2
xxxx
i
i
xxg

13
Пустьзадан исходный полином
0
1
1
1
1
MxM
k
x
k
MxM
исходного
информационногосообщения. Пустьзаданполином )(xR , вычисленныйкакостатокот
деленияполинома
xM , сдвинутогона
r
позицийвлево(другимисловами, умноженногона
r
x ), напорождающийполином
xg . Инымисловами, пустьзаданполином:
1
0
mod
r
i
i
x
i
RxgxM
r
xxR
ТогдакодомРида-Соломонаназываюткоэффициентыинформационногополинома
xM иполиномаостатка
xgxM
r
xxR mod
, представленныевследующемвиде:
Следуетотметить, чтотакоекодированиеназываетсясистематическимвсилутого,
что«информационные» коэффициентыможнолегкоотделитьоткоэффициентовостаткабез
какого-либоспециальногодекодирования.
Говоря втерминологии криптографии, кодРида-Соломона– нечто иноекак,
исходноесообщениеиприсоединенныйкнемунекий«хэш»,вычисленныйпосообщению.
Нетруднозаметить, чтокодРида-Соломонапредставляеткоэффициентынекоторого
полинома
xF вычисляемогокаксуммасдвинутогона
r
позицийвлевоинформационного
полинома
xM иполиномаостатка )(xR :
xRxM
r
xxF
Относительно полинома
xF , в теории кодирование делается два достаточно
простых, новтожевремячрезвычайноважныхутверждения:
Полином
xF делитсябезостатканапорождающийполином
xg .
Полином
xF имееттежекорни, чтоиполином
xg : элементы:
r
2,
2
2,
1
2 .
Какпервое, такивтороеутверждениеособенноважны тем, чтоименнонанеми
базируетсявся логика обнаружения ошибок. Если коэффициенты полинома
xF не
искажены, тоегоделениенапорождающийполином дастнулевойостаток, такжекак
подстановкавнеголюбогоизкорнейпорождающегополиномаобратитеговнуль. Еслиже
коэффициентыполинома
xF былиискажены(припередачепосетиилиприхранениина
носителеинформации), тосоченьвысокойвероятностью, априискажениинеболее
r
байтовсо100% гарантией, делениенапорождающийполиномдастненулевойостаток, также
какиподстановкакорнейпорождающегополиномабудутдаватьненулевыерезультаты.
Здесьработаеттатехническаяуловка, что«окружающаясреда», конечно, враждебнак
нашейинформацииипытаетсяслучайнымнепредсказуемымобразомееискажать, но«она
ненастолькоумна», чтобыискажатьинформациютак, чтобыискаженныйполином, также
какинеискаженныйполиномделилсябезостатканапорождающийполином. Слишкомуж
«мудрыерасчеты», иокружающаясредаужточновних«невникает» (вотличие, кстати, от
человека-злоумышленника), она просто «портит» данные случайным образом и все.
Вероятностьтого, чтоискаженный полином разделитсябезостатканапорождающий
полином, весьма невелика при искажении более
r
байтов, и с увеличением числа
избыточныхбайтонастановитсяещегораздоменьше, априискажениинеболее
r
байтов,
вероятностьтакогоисходавообщенулевая– этотеоретическидоказаноиэкспериментально
подтвержденосоответствующимиучеными-специалистами.
M
k – 1
… M
0
R
r – 1
… R
0
14
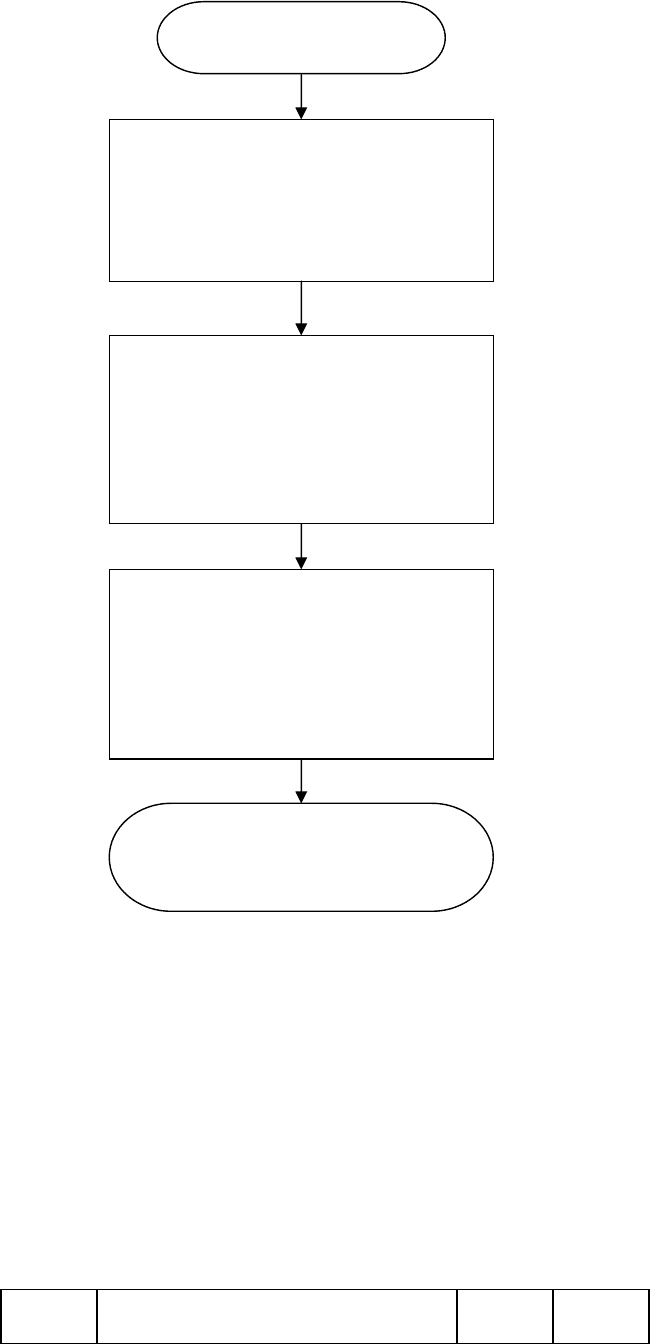
Тогдасучетом вышесказанногоможем представитьнесложную схемуалгоритма
кодирования(рис. 1) информационныхсообщенийсприменениемкодовРида-Соломона,
призаданнойдлинесообщения– k имаксимальнойкратностиисправляемойошибки–
t
.
Рис. 1. Схемаалгоритмакодированияинформационного
сообщениясприменениемкодаРида-Соломона
Припередачекадрапосетиилиприхранениикадраданныхнаносителе, информация
можетбытьискаженавсилутехилииныхфизическихпричин: шумывканалепередаче
данныхилиповреждениеносителяданных. Втакомслучаеможноговорить, чтонакадрF
будетналоженонекотороеискажениеE, илиинымисловами, полиномкадра
xF будет
складыватьсявместеснекоторым, такназываемым, полиномом искажения
xE и в
результате будем иметь искаженный полином
)()( xExFxC намоментприема
сообщенияизсетииличтенииданныхсносителя. Искажатьсямогутлюбыекоэффициенты
полинома(байтыкадра), какинформационные, такиизбыточные.
Витогебудемиметь, такназываемый, искаженныйкадрC.
tr 2
Вычислениеполинома
)
2
(
2
1
2
8
GF
r
i
i
xxg
Преобразованиеисходного
сообщенияM длиныk
вполином )(xM ивычисление
xgxM
r
xxR mod
Формированиеполинома
xRxM
r
xxF
и
преобразование
вкадрF длиныn = k + r
ПередачакадраF посети
илизаписьнаноситель
С
n – 1
…
C
0
C
1
15
4. ДекодированиекодовРида-Соломона
Пусть имеется кадр длины rkn
, состоящий из k информационных и
r
избыточныхбайтов, принятыйизсетиилисчитанныйсносителя, полином
xC которого
являетсясуммойполинома )(xF исходногонеискаженногокадра, отправленногопосетиили
записанногонаноситель, инекоторогополиномаискажения )(xE :
)()( xExFxC
Тогдабудем называтьсиндромом ошибки(синдром – совокупностьсимптомов,
характеризующеезаболевание) коэффициенты rj
j
S 1, , вычисляемыеподстановкойв
полином
xC корней
r
2,
2
2,
1
2 порождающегополинома
xg .
Тогдаполиномсиндромаошибок
xS можетбытьпредставленкак:
r
j
j
x
j
CxS
1
1
)2(
Заметим, чтокоэффициентыполиномасиндроманумеруютсяс1 по
r
. Крометого,
учитываято, чтомыранееустановили, чтополином )(xF неискаженногокадраобращается
внульприподстановкевнегокорней
r
2,
2
2,
1
2 , тосправедливоследующееравенство:
rj
j
E
j
C
j
S
1
)2()2(
Инымисловами, синдромнезависитотсамогонеискаженногокадраF иполностью
характеризуется только ошибкой E. Именно на этом и базируется вся технология
расшифровкисиндромасцельюнахожденияместоположенияошибокиихзначений.
Однако, несмотрянато, чтокоэффициенты синдроматаклегкоопределяютсяпо
полиному искажения )(xE , обратное же вычисление полинома )(xE по известным
коэффициентамполиномасиндромаошибок
xS весьмасложнаяинетривиальнаязадача.
Ситуацияухудшаетсяещетем, чтонеизвестносколькоименнобайтовбылоискажено.
Пусть,
– предполагаемоеколичествоискаженныхбайтоввкадреC.
Очевидно, чтоеслиполиномсиндромаравеннулю
0xS (всеегокоэффициенты
нулевые), томожноговорить, чтоискаженийлибонебыло, либопроизошлоискажение, не
обнаруживаемоепризаданномколичествеизбыточныхбайтоввсилутого, чтократность
произошедшейошибкибольшекратностьобнаруживаемойошибки, тоесть tr 2
.
Впротивномслучае, еслисиндромненулевой, томожнодекодироватьего. Введем
понятие, такназываемого, полиномалокаторовошибокследующеговида:
1
21
1
1
i
i
u
i
x
i
i
x
i
x
Очевидно, чтокорнямиполиномалокатораявляютсяэлементы
uu
2,,
1
2 , и
согласно теории кодированиясами степени
uu ,,
1
, этонечтоиное, как локаторы
местоположенияошибоквпринятомизсети(считанномсносителя) кадреС.
Согласнотеориикодирования, коэффициентыполиномасиндрома
xS иполинома
локаторов
x связанытакназываемойключевойсистемойуравненийдекодирования:
tj
i
ij
S
ij
S
21
1
16
Еслипереписатьсистемувразвернутомвиде, тоэтасистемавыглядиттак:
t
S
t
S
t
S
SSS
SSS
22121
2211
111
Каквидим, этонепростосистемауравнений, асистемаиз
t2 уравненийс
неизвестными, причемсампараметр
неизвестен.
При 0
, случайотсутствияошибок, системавырождается, инечегорешать.
При t
1 , системаимеетоднозначноерешение, поскольку число уравнений
ttt 12)2(
больше либо равно (при
t
), чем соответствующеечисло
неизвестных t1
. Предельныйслучай, когдасистемавсеещеимеетоднозначное
решение– это
t
, приэтомимеем
t
уравненийи
t
неизвестных.
При 121
tt
, системанеимеетоднозначногорешения, посколькучисло
уравнений 11)2(
tt
, оказывается меньше, чем число неизвестных
121
tt
, иоднозначноенахождениелокаторовстановитсяневозможным.
При t2
, системаопятьжевырождается, ирешениеневозможно.
Задачанахожденияполиномалокаторовмоглабыпривестикнеобходимостиполного
переборавсевозможныхрешенийприразличных 121
t
, однако, здесьсноваприходит
напомощьтеориякодирования. Онаутверждает, чтолибооднозначногорешенияне
существует, либосуществуетоднозначноерешениепри t
1 , иприэтомподходитне
первоепопавшеесярешение, аторешение, прикоторомстепеньполиномалокаторов
x ,
равная
, минимальна. Согласно теории именно в этом случае, полином локаторов
наименьшейстепени, коэффициенты которогоудовлетворяютвсейсистемеуравнений, и
являетсяистиннымполиномомлокаторовошибок.
Тогда, окончательно, имеемследующуюматематическую модельзадачинахождения
полиномалокаторов– система
t2 уравнений с
неизвестными с минимизацией
параметра
– степениполинома-решения(онажеипредполагаемаякратностьошибки).
)(
21
min)(deg
1
x
tj
x
i
ij
S
ij
S
Коды Рида-Соломонаиоснованныенанихметоды кодирования, обнаруженияи
исправленияошибокнеполучилибы широкогораспространение, еслибы всвоевремя
ученыеБерлекэмпиМессив1968-1969 годахнепредложиличрезвычайноэффективный
алгоритм[3, 8, 9] решенияэтойзадачи, которыйнаходитрешениенеболеечемза t2 шагов.
ИменноэтотмоментможносчитатьначаломмассовогоприменениякодовРида-Соломона
дляобнаруженияи исправленияошибок. Доэтоговсилудостаточноймедлительностии
сложностиваппаратнойреализации существующих натотмоменталгоритмовпоиска
полиномалокаторов, восновномобходилисьтольковычислениемсиндромовсцельютолько
обнаруженияошибки. Вслучаеобнаруженияошибкиделаласьпопыткаповторногозапроса
кадра, еслиэтобыловозможно, впротивномслучаевыдавалосьсообщениеобошибке.
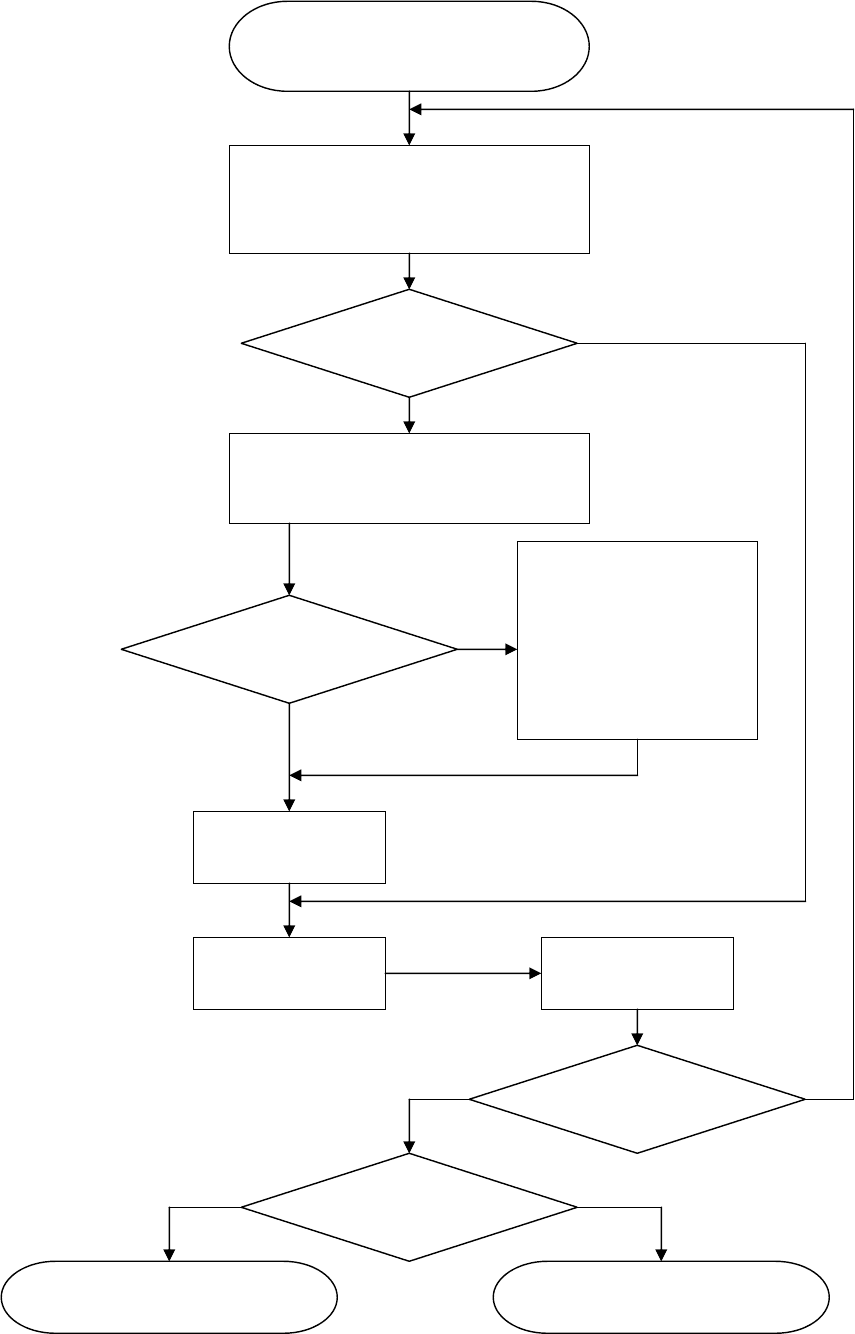
17
Рис. 2. СхемаалгоритмаБерлекэмпа-Мессидлянахожденияполиномалокаторов
1,0,0
)(,1)(
mLq
xxBx
L
i
iq
S
iq
0
1
?0
q
)()()(
*
xB
q
xx
?mqL
?2tq
?
deg
L
x
)(
*
)( xx
)()( xBxxB
1
qq
)(
1
)(
*
*
x
q
xB
LL
Lqm
mqL
Да
Нет
Нет
Нет
Да
Да
Да
Нет
(x) ненайден
(x) найден

18
ВалгоритмеБерлекэмпа-Месси(рис. 2) используютсяследующиеобозначения:
j
S – коэффициентысиндромаошибки.
x – рассчитываемыйполиномлокаторов.
q
– номеритерацииалгоритма.
q
– значениеневязки, этонечтоиное, каксуммалевойиправойчасти
го
q
уравнения, котораяобращаетсявнуль, еслиполиномлокаторовудовлетворяетуравнению.
m
– номершага, накоторомполиномлокаторапоследнийразмодифицировался.
L
– количествочленоввлевойчастиуравнений, фактическиэтотпараметротражает
количество
искаженныхбайтов, предполагаемоевовремяитерацийалгоритма.
xB – полином модификации, который используетсякак вспомогательный для
модификацииполиномалокаторовдля«подстройки»егоподуравнениясистемы.
Алгоритм достаточно нетривиален. Начиная с полинома локаторов
1x ,
вычисляется, так называемая, невязка (расхождение, несоответствие) этого полинома
первомууравнению. Далееучитываяэтуневязку, делаетсякоррекцияполиномалокаторов,
принеобходимостинаращиваетсяегостепень, адальшевсеповторяетсятак, чтобыпри
условии удовлетворениявсех предыдущих уравнений, он такжестал удовлетворятьи
текущемууравнению, и такдотехпор, поканебудутудовлетворены всеуравнения.
Посколькувалгоритместепеньполиноманаращиваетсятолькопринеобходимости, то
решениемибудетполиномминимальнойстепени.
Врезультатеработы алгоритма, вслучае, еслинастоящееколичествоискаженных
байт больше, чем максимальное количество исправляемых ошибок, возможно (но
необязательно), чтостепеньполиномалокаторовнебудетсовпадатьспредполагаемым
количествомискаженныхбайт, вэтомслучаесчитается, чторешениесистемыуравненийне
найдено. Этотслучайследуеттрактовать, какневозможностьисправленияошибок.
Вслучаееслиполиномлокаторов
x исоответствующаяпредполагаемаякратность
ошибки
найдены, тодальнейшеедекодированиелокаторовошибокнепредставляет
особойтрудности. Дляэтогополиномлокаторовприравниваетсянулю, инаходятвсекорни
uu
2,,
1
2 уравнения. Делаетсяэтополнымперебором элементов
255
2,,
1
2 поля
Галуаиподстановкойкаждогоизних вполином локаторов, еслиполином локаторов
обращаетсявнуль, то, значит, найденодинизкорней. Посколькупереборсоставляетвсего
255 итераций, такойподходвполнеоправдан. Наконец, понайденнымкорням, выделяются
ихстепени
uu ,,
1
, и, темсамымвычисляютсялокаторы:
uuU
uu
xΛ(x) ,,
1
2,,
1
2*0
Послевычислениялокаторов, следуетвыполнитьпроверкукаждого локаторана
условие
1],1,0[ ln
l
u , инымисловамилокаторнеможетбыть«указыватьзапределы
кадра». Еслихотябы одинизнайденныхлокаторов«указываетзапределы кадров», то
считается, чтодекодированиепрошлонекорректноиисправлениеошибокневозможно–
такоепроисходиттолько, еслиопятьженастоящееколичествоошибок, вдействительности,
больше, чеммаксимальноеколичествоисправляемыхошибок.
Важноепримечание. Конкретнодлякодов Рида-СоломонавполеГалуаGF(2
8
)
локаторыошибокмогутприниматьзначениятольковпределахот0 до254, посколькусами
являются, посути, логарифмамиотэлементовполеГалуаGF(2
8
), числокоторыхконечно. Из
этогоследуеточеньважноеограничениедляприменениякодовРида-СоломонавполеГалуа
GF(2
8
), длинакадрадолжнабытьменьшелиборавна255, тоесть 255
rkn . Впрактике
такоесерьезноеограничениеобходитсяпутемразбиенияданныхнамножествонебольших
кадров(блоков), длинакоторыхменьше255 икодированияихпоотдельности.

19
В случаеуспешноговычислениялокаторов
uu ,,
1
ошибок, остаетсяпоследняя
задача: вычислениязначенийошибок. Посколькумыимеетделонесбитами, сбайтамив
каждойпозициикадра, тозначениябайтаможетисказиться256 различнымиспособамии
величинуискажениянеобходимовыяснитьдлякаждогонайденноголокатораошибок.
В теории кодирования для вычисления величин ошибок используется, так
называемый, методФорни[4, 8, 9].
Вводится, такназываемый, полином величин ошибок –
x , которыйсвязан,
согласно теории, сполиномом синдрома
xS иполиномом локаторов
x ошибок
следующимуравнением:
r
xxxSx mod
Операциявычисленияостаткапомодулю
r
x фактическиэтонечтоиное, какпростое
обнулениевсехкоэффициентовсиндексами
r
i
, ииспользованиепроцедуры деления
полиномовздесьсовсемизлишне. Послеперемноженияполиномасиндромаиполинома
локатора, коэффициенты с индексами ti 2
результирующего полинома-произведения
обнуляются, ирезультатпереписываетсявкоэффициентыполинома
x .
Вводитсятакже, такназываемая, формальнаяпроизводнаяполиномалокаторов–
x
, котораявычисляетсяследующимобразом:
02mod,
2
1
12mod,
1
2
31
x
x
xx
dx
d
x
Тогдавеличины ошибок
vv ,,
1
впозициях, указываемыхлокаторамиошибок,
вычисляются, как отношение значения полинома
x величин ошибок к значению
производной
x
полиномалокаторавсоответствующихкорнях
1,2
l
l
u
.
]255,1[,,,
1
1
22
l
vvvV
l
l
u
l
u
v
l
Таким образом, вычисляютсявеличины
vv ,,
1
ошибок. Послеэтогонетрудно
сформироватьполиномискаженийпоизвестнымлокаторамивеличинамошибок.
τ
l
l
u
x
l
vxE
1
Наконец, последнеечтоостается– этосложитьполиномкадра(принятогоизсетиили
считанногосносителя) сполиномом искаженийитемсамымосуществитьисправление
ошибокивосстановлениеисходногополиноманеискаженногокадра:
xExCxF
Нижепредставленасхемаалгоритмадекодирования(рис. 3).
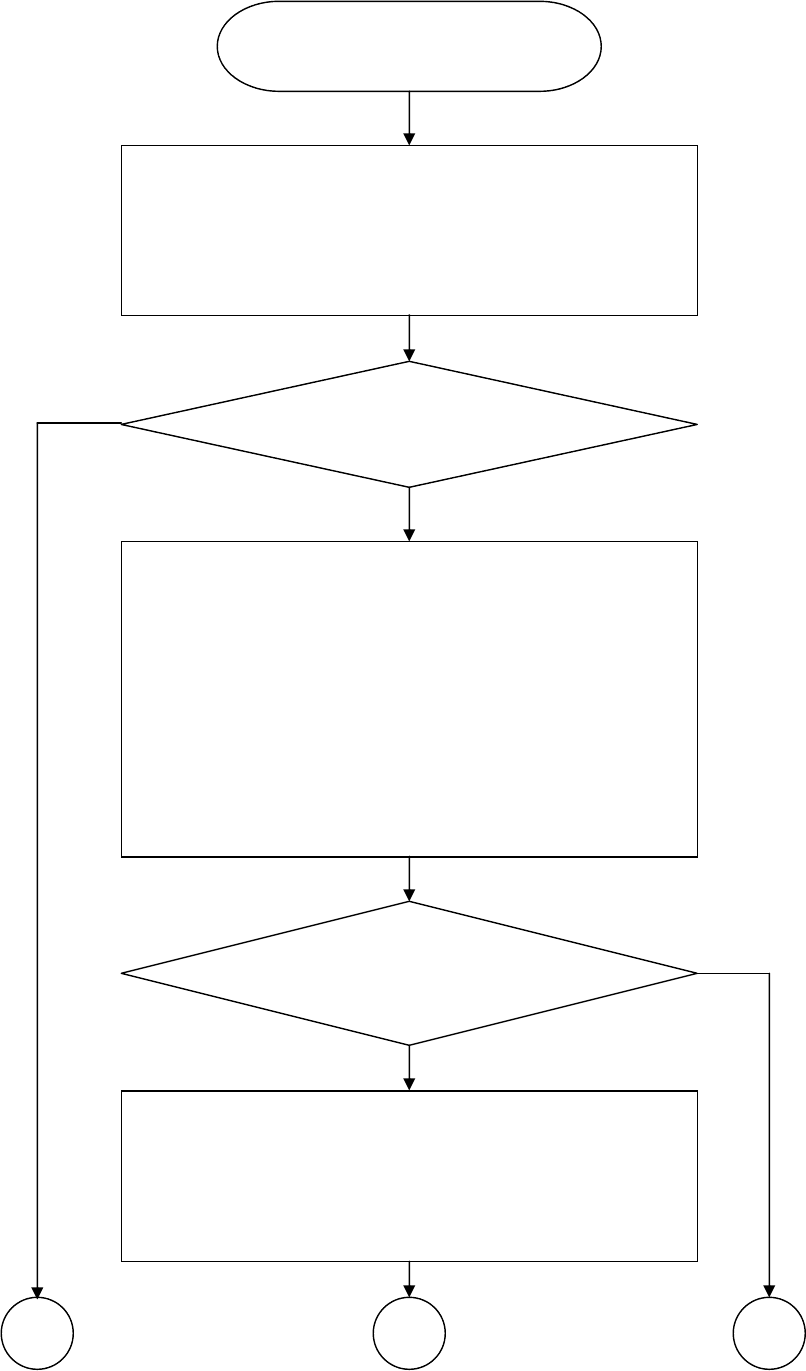
20
Рис. 3. СхемаалгоритмадекодированиякодаРида-Соломона(начало)
ПреобразованиекадраC длиныn = k +r
вполином )(xC ивычисление
коэффициентовполиномасиндрома:
rj
j
C
j
S 1),2(
Формированиеключевойзадачидекодированияи
нахождениеполинома )(x
локаторовошибок
поалгоритмуБерлекэмпа-Месси
)(
21
min)(deg
1
x
tj
x
i
ij
S
ij
S
ПриемкадраC изсетиили
считываниесносителя
Полином )(x
локаторовнайден?
Нахождениекорнейуравнения 0)(
x :
uu
2,,
1
2 ивыделениелокаторов
uu ,,
1
Проверкалокаторовнаусловие ]1,0[ n
l
u
Да
Нет
32
Все ?1,0 rj
j
S
Нет
Да
1
