Пятковский О.И. Интеллектуальные информационные системы (нейронные сети)
Подождите немного. Документ загружается.


31
пусков средневыборочными по присутствующим значениям с помощью рег-
рессии и главных компонент [102]. Эти методы в общем случае имеют малую
эффективность, ведут, как правило, к несмещенности и несостоятельности, к
нарушению уровней значимости критериев и другим искажениям статистиче-
ских выводов, не обладают устойчивостью к распределению пропусков. Наибо-
лее популярным в настоящее время за рубежом является EM –алгортм [98] . В
нашей стране известны работы в области заполнения пропусков в данных, в
том числе, наиболее эффективными являются алгоритмы ZET, адаптивный ге-
нетический алгоритм LGAP [60].
Для проводимых исследований за основу взята работа[184]. Авторами
этой работы создан программный комплекс «Линейный и нелинейный фактор-
ный анализ». Он предназначен для восстановления пропущенных (ремонт из-
вестных) данных в таблицах путем моделирования исходных данных многооб-
разиями малой размерности и последующего замещения пропущенных данных
значениями из модели. Метод интерпретируется как построение конвейера
нейронов для обработки данных с пробелами. Другая возможная интерпретация
- итерационный метод главных компонент и нелинейный факторный анализ для
данных с пробелами.
Следующим элементом предобработчика является оценка выборки и, при
необходимости, фильтрация данных. Данные методы обсуждались в третьей
главе работы. В зависимости от характера обучающей выборки возможно ис-
пользование различных методов фильтрации данных. Для выбора методов не-
обходимо произвести предварительную оценку данных. Для этого можно ис-
пользовать оценку дисперсии, эвристические методы. В зависимости от резуль-
татов анализа при помощи экспертной системы (продукционной, основанной на
теории прецедентов и др.) определяется тот или иной метод фильтрации дан-
ных: простые скользящие средние, взвешенные скользящие средние, экспонен-
циальное скользящее среднее, фурье, вейвлет –анализ и т.д [57,102,222].
Заключительным этапом предобработки является нормировка данных.
При этом осуществляется преобразование входных сигналов таким образом,
чтобы обеспечить эффективную работу нейронной сети. Для количественных
признаков стандартными процедурами предобработки являются нормировка и
центрирование, которые обеспечивают универсальность нейронной сети при
работе с произвольными данными и позволяют сохранять параметры сети в оп-
тимальном для функционирования диапазоне. Существует несколько стандарт-
ных методов нормировки [41], использующих оценки математического ожида-
ния и дисперсии, основанные на текущей выборке, но оценки статистических
параметров могут меняться от выборки к выборке, что создаст трудности при
обработке новых данных, которые могут менять статистические параметры вы-
борки. Более удобной в нашем случае является формула [41, 110]:
(
)
(
)
( )
min
minmax
minmaxmin
b
xx
bbxx
x +
−
−
−
=
−
,
(
4.3)

32
где [b
min
,b
max
] - диапазон приемлемых значений входных переменных, в
нашем случае [-1,1]; [x
min
,x
max
] – интервал допустимых значений признака x, по-
лученный на этапе структурирования,
x
–преобразованный сигнал, который бу-
дет подан на вход сети. При использовании (4.3) параметры нормировки оста-
ются неизменными при обработке различных выборок.
Значения переменных, измеренных в номинальной шкале, обычно пред-
ставлены в обучающей выборке в виде натуральных чисел 1 .. S, где S – число
возможных состояний. Преобразование номинальных переменных по формуле
(4.3) некорректно, так как явным образом вводит расстояние между отдельны-
ми значениями переменной.
Применяется следующий метод предобработки. Пусть Р
∈
{1..S} –
номинальная переменная, S – число возможных состояний. C=(C
1
.. C
S
),
C
i
∈
{-1,1} – кортеж бинарных переменных. Тогда каждой Р
k
ставится в соот-
ветствие C
k
. При этом
P
k
= i ⇒
⇒⇒
⇒ C
i
k
=1, C
j
k
=-1,
∀
j
≠
i; i,j = 1 .. S,
(4.4)
где i, j – номера состояний Р
k
. В итоге, каждой номинальной переменной
соответствует несколько бинарных полей в обучающей выборке.
Преобразования (4.3), (4.4) проводятся как для входных, так и для выход-
ных параметров обучающей выборки.
В [41, 110] предлагается включить в предобработку данных вычисление
оценки константы Липшица для выборки для определения «минимального по-
рога разрешения», которым должна обладать нейросеть, чтобы иметь возмож-
ность разделить два близких сигнала:
{ }
21
)
2
()
1
(
2
1
,
2
,
1
sup
xx
xx
xxxx
−
−
≠∈∀
≥
ff
X
s
L ,
(
4.5)
где L
s
– выборочная константа Липшица; x
1
, x
2
– примеры из выборки
X;
(.)f
– значение целевой переменной; ||⋅|| – евклидова норма.
Если x
1
= x
2
при f(x
1
) ≠ f(x
2
), то примеры x
1
, x
2
являются конфликтными
и оценка обучения сети на данной выборке будет не меньше, чем
e
= 0.5 ⋅ (|f(x
1
) − f(x
2
)| )
2
.
Конфликтные примеры свидетельствуют либо об ошибках измерения
различной природы, либо о недостаточности набора параметров для описания
объекта. В первом случае один из примеров исключают из рассмотрения, или,
при малом значении e, продолжают обучение, используя оценку МНК «с до-
пуском» [110]. Во втором случае необходим дополнительный анализ предмет-
ной области для выявления новых параметров описания, позволяющих разде-
лить конфликтные примеры.

33
Если в значениях выходной переменной присутствует аддитивный шум
формула (4.5) может дать завышенную оценку константы Липшица аппрок-
симируемой функции. В этом случае предлагается использовать оценку:
21
21
2)()(
sup
xx
xx
−
−−
≥
ε
ff
L
s
,
(
4.6)
где ||f(x
1
) – f(x
2
)||>2
ε,
т.е. требования к нейросетевой модели станут менее
жесткими, что позволит построить более гладкую нейросетевую зависимость.
Заметим, что использование того или иного вида выборочной константы Лип-
шица зависит от вида функционала оценки работы нейросети. Классическому
МНК соответствует (4.5), при оценке типа МНК с допуском предлагается ис-
пользовать (4.6).
Выборка может содержать как количественные, так и номинальные пере-
менные. В случае векторов со смешанным типом компонент расстояние опре-
деляется в соответствии с функцией HEOM (Heterogeneous Euclidean –Overlap
Metric function) [279]: для количественных параметров, после их нормирования
в интервал [-1,1], за расстояние принимается модуль разности значений. Для
дискретных переменных расстояние между двумя значениями P
1
и P
2
перемен-
ной Р определяется по правилу:
21
iii
CCd −=
,
(4.7
)
где
С
1
,
С
2
получены по формуле (4.4). Тогда расстояние между векторами
вычисляется по формуле
∑
=
=
P
i
i
dD
1
2
)( ,
(
4.8)
где i – номер компоненты вектора.
2.3 Формирование задачника для нейросети
Для информационных систем важным является вопрос формирования за-
дачника. Это связано с тем, что для любого интеллектуального блока, которых
в информационных системах довольно много, на входе формируется обучаю-
щая выборка, которая находится в постоянном динамическом изменении. Как
правило, обучение производится не по всему задачнику, а по некоторой его
части. Ту часть задачника, по которой в данный момент производится обуче-
ние, будем называть обучающей выборкой. Важность этого компонента опреде-
ляется тем, что при обучении сетей всех видов с использованием любых алго-
ритмов обучения необходимо предъявлять примеры, на которых она обучается
решению задачи. Кроме того, задачник содержит правильные ответы для сетей,
обучаемых с учителем.
Настройка параметров функции (4.2) производится на основе обучающей
выборки, которая содержит примеры, описывающие состояние объекта иссле-

34
дования, и значения целевого параметра, соответствующие каждому состоя-
нию. Например, для задач оценки деятельности конкретного ВУЗа наиболее
характерно применение временных отсчетов в качестве базового параметра из-
мерения, т.е. примеры значений параметров объекта отличаются тем, что изме-
рены в различные моменты времени. Соответствующая обучающая выборка
представляется в виде матрицы M:
=
ppp
tt
n
t
tt
n
t
p
yxx
yxx
t
t
M
L
MMLM
L
M
1
11
111
;
pittt
конiнач
,1, =≤≤
,
где
нач
t
и
кон
t
– границы временного интервала, определяемые экспертным
путем.
Важным вопросом является разделение всех доступных данных на обу-
чающую и тестовую выборки таким образом, чтобы обеспечить их независи-
мость и представительность. Эта проблема решается для каждой конкретной
задачи отдельно. Задачник формируется в результате функционирования ин-
формационной системы в ритме процессов производства и управления. Форми-
рование происходит непосредственно в базах данных, причем даже для одного
АРМа их может быть несколько.
Для рассматриваемых информационных систем основной структурой за-
дачника является база данных реляционного типа. Каждому примеру соответ-
ствует одна запись базы данных. Каждому данному - одно поле. Поля базы
данных могут быть числовыми и текстовыми. В зависимости от решаемой за-
дачи содержимое задачника может меняться. Так, например, для решения зада-
чи классификации без учителя используют нейросети, основанные на методе
динамических ядер [207] (наиболее известным частным случаем таких сетей
являются сети Кохонена [233,234]). Задачник для такой сети должен содержать
только векторы входных данных. При использовании обучаемых сетей, осно-
ванных на принципе двойственности, к задачнику необходимо добавить вектор
ответов сети. Кроме того, некоторые исследователи хотят иметь возможность
просмотреть ответы, выданные сетью, вектор оценок примера, показатели зна-
чимости входных сигналов и, возможно, некоторые другие величины. Поэтому,
стандартный задачник должен иметь возможность предоставить пользователю
всю необходимую информацию. При формировании задачника должны актив-
но использоваться возможности графики и цвета. [148].
Задачники формируются в результате функционирования информацион-
ной системы в базах данных в ритме процессов производства и управления в
соответствии с разработанными технологиями. При этом выполняются проце-
дуры погружения данных, описанные выше. Например, для задач прогнозиро-
вания возможны следующие варианты погружения информации: без пересече-
ния, с пересечением, с дообучением, без дообучения, по совокупности времен-

35
ных рядов, в том числе возможны варианты с учетом сезонных колебаний, с
учетом других качественных признаков (рис. 4.14). При организации задачни-
ков важными являются вопросы создания и обновления архивов, технологии
формирования обучающих выборок по этапам технологического процесса об-
работки информации в автоматизированной системе.
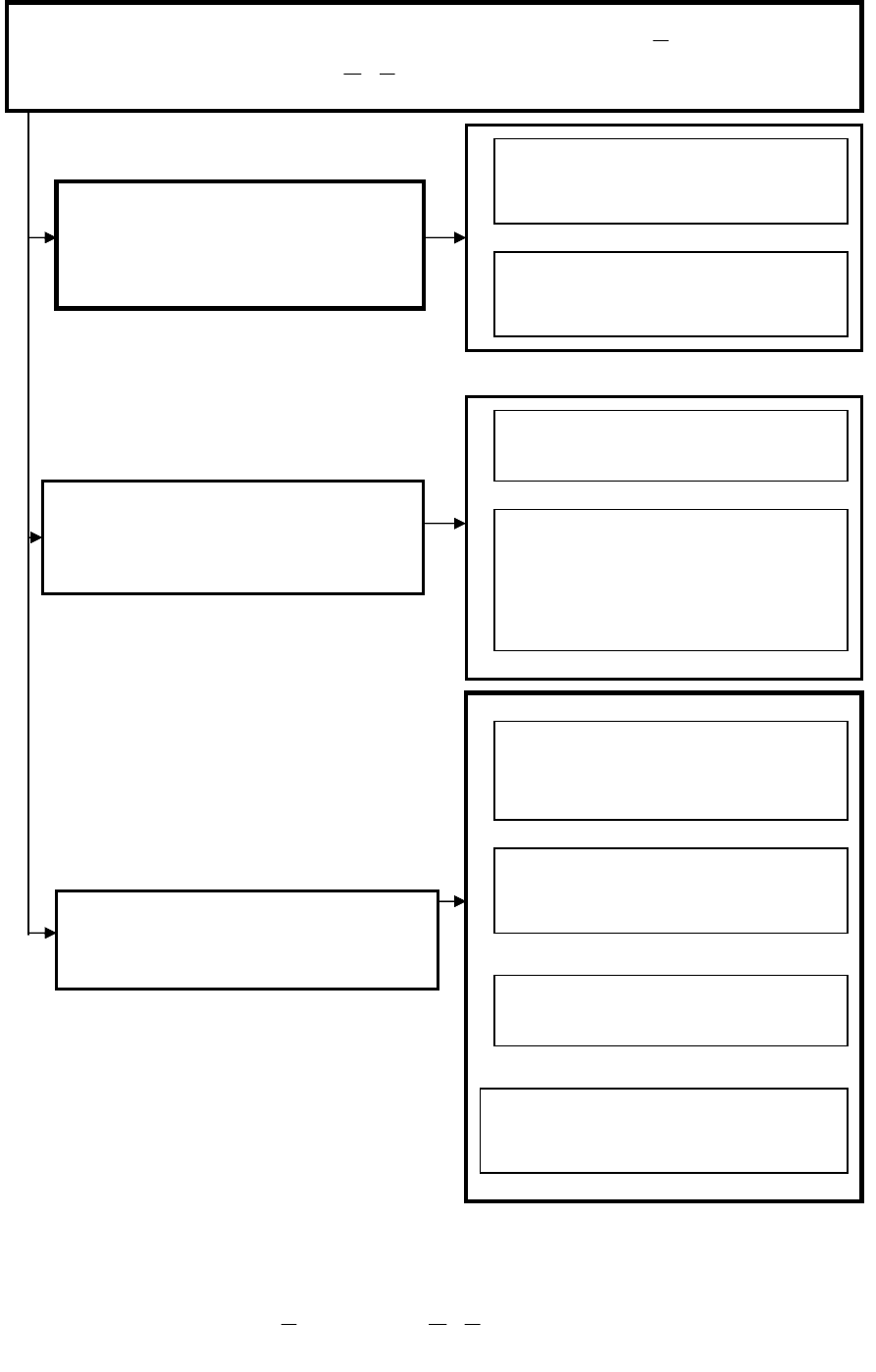
На рисунке (4.14) представлены методы формирования выходных (целе-
вых) параметров
Y
задачника нейросети. Наиболее качественные данные задач-
ника получаются на основе фактической выборочной, экспериментальной ин-
формации, в том числе по данным происшедших событий, выполненных опы-
тов и экспериментов. При решении неформализованных задач, таких
,например, как оценка состояния объекта управления, получение значения це-
левого параметра экспериментальным путем бывает невозможно. В этом случае
используется экспертная информация, формируемая опытным специалистом в
соответствующей области знаний или группой экспертов при помощи методов
экспертной оценки [54].
При функционировании информационной системы, при постоянно изме-
няющемся состоянии предметной области, существенном обновлении данных
задачника часто не представляется возможным своевременно привлечь опыт-
ных специалистов для выработки значений целевых параметров и последующе-
го дообучения нейронной сети. Для этого в работе разработаны методы авто-
матического самообучения нейросетевых компонентов(рис.4.15). Они реализу-
ются при помощи специально разработанных экспертных систем, содержащих
знания опытных специалистов, по аналитическим методикам и зависимостям, с
использованием фиксированных констант и множеств, определяющих значения
целевых параметров "по умолчанию". На рисунке 4.15 представлен процесс
функционирования нейросетевого решателя в режиме автоматического обуче-
ния. В данной схеме показано подключение экспертной системы для формиро-
вания значений целевого параметра
Y
перед дообучением нейронной сети. Од-
нако следует отметить, что данный режим не должен быть
36
Методы формирования выходных параметров
Y
задачника
(
)
Y
X
|
нейросети
Фактическая выбо-
рочная и эксперименталь-
ная информация
по данным происшедших собы-
тий
по данным выполненных опы-
тов и экспериментов
Экспертная информация
при автоматизированном
обучении
Определение экспертом
Определение группой
экспертов при помощи
методов экспертной
оценки
Методы автоматического
самообучения
При помощи экспертной сис-
темы
По методикам
специалистов
По известным аналити-ческим
зависимостям
С использованием фиксирован-
ных констант, множеств
Рис. 5.14. Методы формирования выходных параметров
Y
задачника
(
)
YX |
нейросети
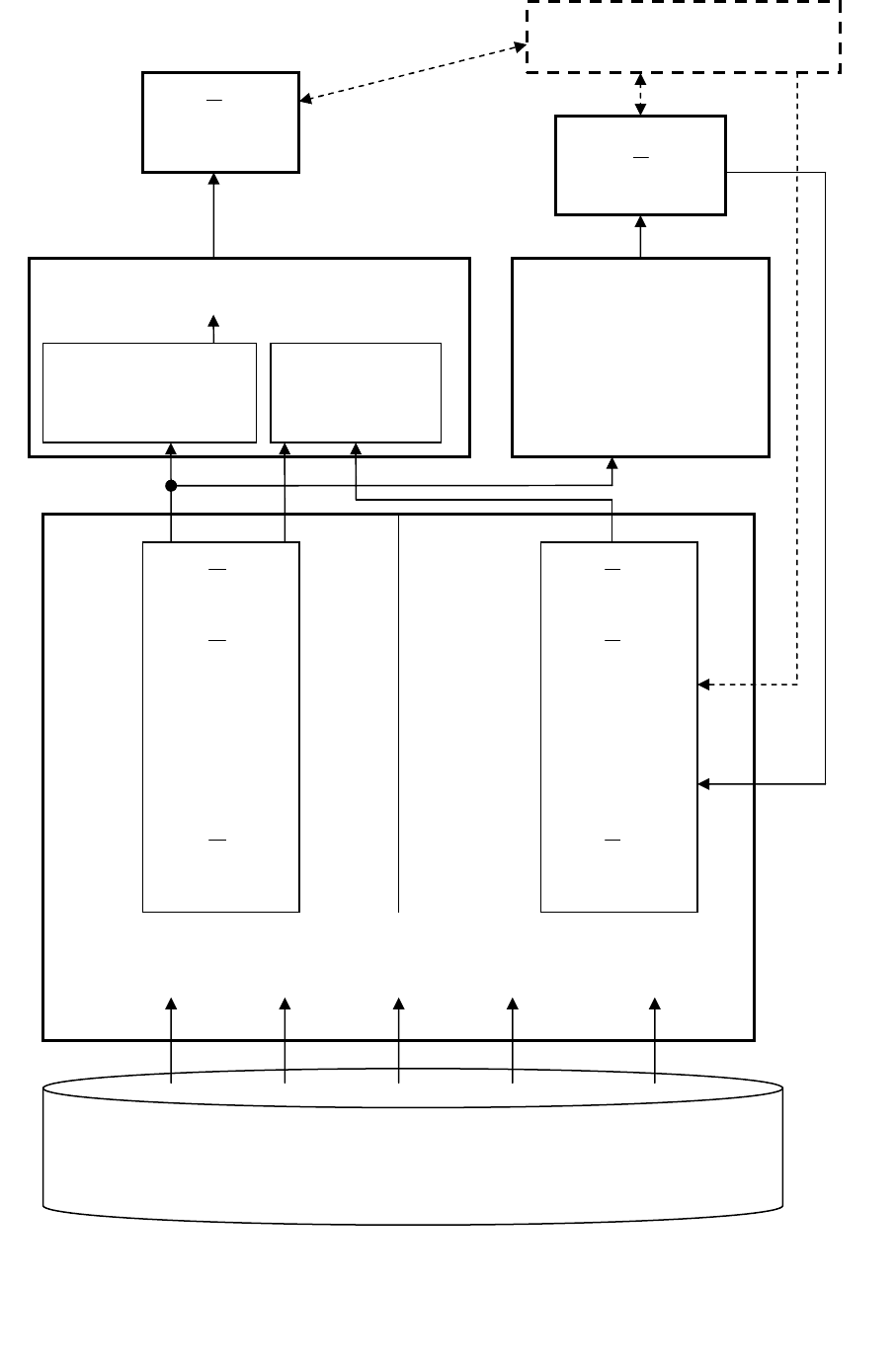
37
НЕЙРОННАЯ СЕТЬ
ЭКСПЕРТНАЯ
СИСТЕМА
ЭКСПЕРТ
БАЗА ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ
Y
O
Y
…
…
…
1
X
n
X
2
X
…
…
…
O
Y
1
O
Y
2
O
n
Y
ОБУЧАЮЩАЯ (ТЕСТОВАЯ) ВЫБОРКА
Блок
тестирования
Блок
обучения
Рис. 5.15. Функционирование нейросетевого решателя в режиме
автоматического обучения
38
основным. В реально работающих информационных системах режим са-
мообучения не должен иметь регулярного характера, так как при этом качество
обучения нейросетевых элементов ухудшается. При эксплуатации информаци-
онных систем периодически должны подключаться группы экспертов для об-
новления целевых параметров обучающих выборок и последующего дообуче-
ния нейросетевых компонентов.
2.4 Особенности формирования нейронной сети
При построении нейроимитаторов основным их элементом является ис-
кусственная нейронная сеть[ 41]. В работе используются два типа сетей: мно-
гослойные сети и карты Кохонена. Архитектура сетей Кохонена и методы их
обучения представлены в работах [92,93,233,234]. Архитектура и алгоритмы
обучения многослойных сетей также широко представлены в литературных ис-
точниках [40,41,228].
2.5 Интерпретация сигналов нейронной сети
Заметим, что если привычный для человека способ представления вход-
ных данных непригоден для нейронной сети, то и формат ответов нейронной
сети часто малопригоден для человека. Необходимо интерпретировать ответы
нейронной сети. Интерпретация зависит от вида ответа. Так, если ответом ней-
ронной сети является действительное число, то его, как правило, приходится
масштабировать и сдвигать для попадания в нужный диапазон ответов. Если
сеть используется как классификатор, то выбор интерпретаторов еще шире.
Важность данного этапа нейросетевой обработки данных вызывает необходи-
мость выделения интерпретатора ответа нейронной сети в отдельный ком-
понент нейрокомпьютера. Особое значение имеет данный компонент при рабо-
те нейрокомпьютера в составе информационной системы ВУЗа. Интерпретатор
ответа напрямую взаимодействует с пользователем, поэтому оттого, как каче-
ственно будет организован интерфейс, зависит эффективность его работы. В п.
4.2 описан один из подходов к построению интеллектуальных интерфейсов.
Кроме того, насущным становится применение современных информационных
технологий мультимедиа.
Интерпретатор ответа напрямую взаимодействует с пользователем, по-
этому оттого, как качественно будет организован интерфейс, зависит эффек-
тивность его работы. Для информационных систем выделяются следующие
блоки интерпретации: восстановление данных, семантическое представление,
шкалирование, графическое, аудио, видео, мультимедиа – представление. Не-
обходимо уделять также особое внимание разработке объяснительных компо-
нентов и качественного синтаксиса и семантики выходного языка (Рис. 4.16).
Разработка данных положений является перспективным направлением данной
работы в области совершенствования человеко - машинных интерфейсов ин-
формационных систем.

39
Рис. 5.16. Функции интерпретации выходного сигнала нейросети
ФУНКЦИИ ИНТЕРПРЕТАЦИИ ВЫХОДНОГО СИГНАЛА
НЕЙРОСЕТИ
Шкалирование
Семантическое представление
Графическое представление
Аудио-представление
Видео - представление
Мультимедиа-представление
Объяснительный компонент
Семантика и синтаксис выходного языка
Восстановление данных

40
2.6 Управляющая программа (исполнитель)
Каждый компонент нейрокомпьютера представляет собой отдельный мо-
дуль. Для управления работой нейросетевой системы используется управляю-
щая программа, которая выполняет функции загрузки модулей, организации
обмена информацией между модулями, базами данных и знаний. Данный ком-
понент называется управляющим модулем (менеджером)
.
Задача этого компо-
нента – управление работой программного комплекса нейрокомпьютера, обес-
печивающее эффективное взаимодействие всех его составных частей.
2.7 Компонент учитель
Рассмотрим следующий компонент искусственной нейронной сети –
учитель в режимах обучения и дообучения. Существует ряд алгоритмов обуче-
ния, жестко привязанных к архитектуре нейронной сети. Примерами таких ал-
горитмов могут служить обучение (формирование синаптической карты) сети
Хопфилда, обучение сети Кохонена и ряд других аналогичных сетей. Методы
обучения нейронных сетей типа карт Кохонена представлены в работах
[92,93,233,234].
Рассмотрим особенности алгоритмов обучения многослойных сетей, ко-
торые применяются в настоящей разработке. Минимизация функции оценки
выполняется с привлечением градиентных методов оптимизации. Изучению
градиентных методов обучения нейронных сетей посвящено множество работ
[11,40,41,113,200,210,230]. Все градиентные методы объединены использовани-
ем градиента как основы для вычисления направления спуска. Для разработан-
ного нейроимитатора применяются следующие методы: метод наискорейшего
спуска, модифицированный ParTan, квазиньютоновский [40]. При обучении се-
ти градиентными методами в качестве стандартной оценки работы нейросети
(функции ошибки) выступает оценка по методу наименьших квадратов (МНК)
[40,41]:
( )
( )
∑ ∑
= =
−=
S
s
P
p
p
ss
p
s
yxaF
S
H
1 1
2
,
1
,
(
4.9)
где Н – оценка работы нейросети, F
s
p
(
a, x
s
) – значение р-ой компоненты
вектора выходного сигнала нейросети, y
s
p
– требуемое значение, S – число при-
меров, P – размерность вектора
y
.
В [40,41,110] отмечается, что процесс обучения нейросети можно значи-
тельно ускорить, если вместо оценки (4.9) применять более специализирован-
ные. Они строятся путем формализации требований к нейросетевому решателю
для конкретного вида задач. Для задач регрессии более подходящей является
оценка МНК с допуском [110]:
