Пятковский О.И. Интеллектуальные информационные системы (нейронные сети)
Подождите немного. Документ загружается.


21
На рис.1.10 дана графическая иллюстрация к формулам (5.2), (5.3). Если по-
тенциал нейрона h(t) = 0, то с равными вероятностями реализуются значения
[n(t+1)=1] и [n(t+1)= -1]. Смещение потенциала нейрона в область положительных
значений приводит к увеличению вероятности принять положительное значение
[n(t+1)=1]. Отрицательный потенциал нейрона ведет к увеличению вероятно-
сти [n(t+1)= -1]. На рис.1.10 в качестве примера рассмотрено положительное зна-
чение потенциала h(t) = h.
Рассчитаем математическое ожидание случайного значения выхода n(t+1)
нейрона, если его потенциал равен h(t) (далее в расчетной формуле временной аргу-
мент опускается для краткости записи):
Элементарное преобразование выражения (5.4) приводит к следующей
формуле:
(5.5)
Функция гиперболического тангенса th(x) является
сигмоидальной, ее возможные значения лежат в диапазоне (-1, +1). Построим
детерминированный нейрон, у которого потенциал совпадает с потенциа-
лом стохастического нейрона, а активационная характеристика определяет-
ся формулой:
(5.6)

22
Обозначим выход детерминированного нейрона n:
(5.7)
Сравнение формул (5.5) и (5.7) показывает, что выход детерминированного
нейрона отслеживает среднее значение случайного выхода биполярного стохасти-
ческого нейрона с состояниями +1 и -1. Здесь имеется в виду осреднение по
множеству возможных реализаций биполярных последовательностей на выходе стохас-
тического нейрона.
Если анализируется работа нейронной сети, построенной на стохастических
нейронах, то соответствующая сеть, имеющая в своем составе детерминированные
нейроны с активационными характеристиками - функциями гиперболического тан-
генса, отражает динамику работы стохастической нейронной сети в среднем по
совокупности реализаций. Следует отметить, что сформулированное выше утвер-
ждение является приближенным, так как выражение (5.5) для математического ожи-
дания выхода нейрона вычислялось при условии известного значения потенциала,
в то время как в стохастической нейронной сети потенциалы нейронов также
являются случайными. Фактически вычислялось значение M[n(t+1)|h(t)=h], а
анализ замкнутой сети предполагает вычисление безусловного математического
ожидания M[n(t+1)]. Несовпадение указанных характеристик связано с нели-
нейностью преобразования сигнала нейроном.
1.5 Сравнение характеристик машины фон Неймана и нейронной се-
ти
Машина фон Неймана основана на принципе последовательных вычисле-
ний и эффективно решает задачи числовой и символьной обработки данных.
Однако такие задачи, как распознавание изображений, полученных в разных
масштабах и ракурсах, ассоциативный поиск информации по "обрывоч-
ным" или искаженным данным, принятие интеллектуальных решений в
сложных ситуациях, решаются на последовательных машинах неэффективно. В
то же время мозг человека, включающий в себя низкопроизводительные с
технической точки зрения вычислительные элементы - нейроны с частотой
срабатывания не более нескольких сотен герц, с легкостью справляется с
подобными задачами. Например, задача распознавания лица человека реша-
ется за доли секунды. Такой результат достигается за счет принципиально иной
организации вычислений, основанной на параллельной обработке информации.
В табл. 1 приведены сравнительные характеристики машины фон Неймана
и биологической нейронной сети [3]. Искусственные нейронные сети в некото-
рой степени повторяют особенности функционирования биологических нейрон-
ных сетей. К их числу следует отнести параллелизм вычислений, поиск инфор-
мации по содержанию (ассоциации), а не по месту хранения, адаптация к

23
внешним условиям или самообучение, устойчивость работы при возможных
отказах отдельных вычислительных элементов или нарушении связей
между ними.
Таблица 1
Сравнение машины фон Неймана
с биологической нейронной системой
Машина фон
Неймана
Биологическая
нейронная система
Процессор
Сложный Простой
Высокоскорост-
ной
Низкоскоростной
Один или не-
сколько
Большое количество
Память
Отделена от про-
цессора Локализована
Адресация не по
содержанию
Интегрирована
в процессор
Распределенная
Адресация по
соде
р
жанию
Вычисления
Централизованные
Распределенные
Последовательные
Параллельные
Хранимые про-
граммы
Самообучение
Надежность
Высокая уязви-
мость
Робастностъ
Специализация
Численные и
символьные операции
Проблемы восприятия
Среда функцио-
нирования
Строго опре-
деленная Строго ог-
раниченная
Плохо определен-
ная
Без ограничений
Сравнение времени принятия решения человеком в сложной обстановке (около
1с) с тактом срабатывания нейрона (в среднем около 10 мс) дает основание сделать
вывод, что мозг "запускает" параллельные программы, содержащие около 100
шагов вычислений. Каждый нейрон срабатывает всего несколько раз и не несет основ-
ной информационной нагрузки. Эта нагрузка возложена на связи между нейронами,
которые играют роль "памяти" вычислителя, настраивающейся в процессе обуче-

24
ния и функционирования в изменяющейся внешней среде. Именно эта ведущая роль
связей между нейронами послужила основанием для введения термина коннекционист-
ская модель применительно к искусственным нейронным сетям.
2. Разработка структуры и функций нейроимитатора как элемента ин-
теллектуальной информационной системы
2.1 Концепции применения нейросетевых компонентов в информаци-
онных системах
Рассмотрим развитие методов построения искусственных нейронных се-
тей, предназначенных для проектировании и эксплуатации информационных
систем ВУЗа. В данной главе представлены материалы по разработке струк-
туры и функций нейроимитатора как элемента системы автоматизированного
проектирования и развития аналитических информационных систем. В качест-
ве научной базы для проведенных исследований в области нейронных сетей
взяты работы СО РАН исследователей красноярской группы «Нейрокомп» под
руководством А.Н. Горбаня.
Под искусственной нейронной сетью понимается некоторое вычисли-
тельное устройство обработки информации, состоящее из большого числа па-
раллельно работающих простых процессорных элементов – нейронов, связан-
ных между собой линиями передачи информации – связями или синапсами
[110]. Для автоматизации решения неформализованных задач оценки исполь-
зуются многослойные сети прямого распространения с сигмоидной функцией
активации. Данный класс нейросетей является наиболее исследованным [230].
Для него было доказано утверждение, что сеть, состоящая из входного слоя без
процессорных элементов, «скрытого» слоя с нелинейной передаточной функ-
цией и выходного слоя с линейной функцией активации способна аппроксими-
ровать любую вычислимую функцию [39,230]. Сигмоидный преобразователь
позволяет использовать эффективные методы настойки параметров сети, и
кроме того, нейросети с сигмоидными функциями обладают регуляризующими
свойствами [199].
В контексте данной работы под нейросетью понимается сложная вектор-
функция:
( )
)))))),(,((..(.,,((,
112211
,
0
1
xafaffaxa
−+
=
⋅=
∑
+
kkkk
pi
p
k
ik
k
k
fa
m
i
F
,
(
4.2)
25
где p – номер компоненты выходного вектора, a – вектор пара-
метров или весов связей, x – вектор входных данных или перемен-
ных, k – число слоев сети, m
k
– число нейронов в k-м слое, f
i
r
(a,f
r-1
) –
функция поведения нейрона:
( )
⋅+⋅=
∑∑
−−
=
−
=
−−
mm
rr
j
j
r
j
j
j
r
j
rr
i
afcaff
11
0
1
0
11
,fa , (2)
где с>0 – характеристика пологости функции, r = 1..k – номер слоя сети, i
– номер нейрона, f
0
1.
Технология построения нейросетевых блоков представлена на рис.4.11.
Автором работы [110] для обобщения основных параметров и характери-
стик нейронных сетей вводится понятие нейрокомпьютер. Это понятие опре-
деляется на основе созданного им стандарта. Анализ данной работы показыва-
ет, что при проектировании интеллектуальных информационных систем также
необходимо аналогичное понятие, но с доработкой относительно особенностей
информационных систем. Для информационных систем под нейрокомпьютером
будем понимать интеллектуальный компонент, представленный на рисунке
4.12. Как видно из рисунка, в его состав входят следующие составляющие: ме-
неджер (управляющий модуль), интерфейсы ввода и вывода, предобработчик,
задачник, интерпретатор, нейроимитатор. В состав нейроимитатора входят
следующие элементы: сеть, учитель, контрастер, блок оценки, конструктор
[110]. На рисунке 4.11 показана технология проектирования нейросетевого
компонента. Исследования показали, что все компоненты нейрокомпьютера,
представленные на рисунке 4.12 имеют важное значение при проектировании
и эксплуатации интеллектуальных информационных систем. При этом сущест-
венно доработаны такие компоненты нейрокомпьютера, как предобработчик,
задачник, интерпретатор и исполнитель и введено понятие конструктор. Кроме
режима обучения при настройке компьютера в процессе проектирования ин-
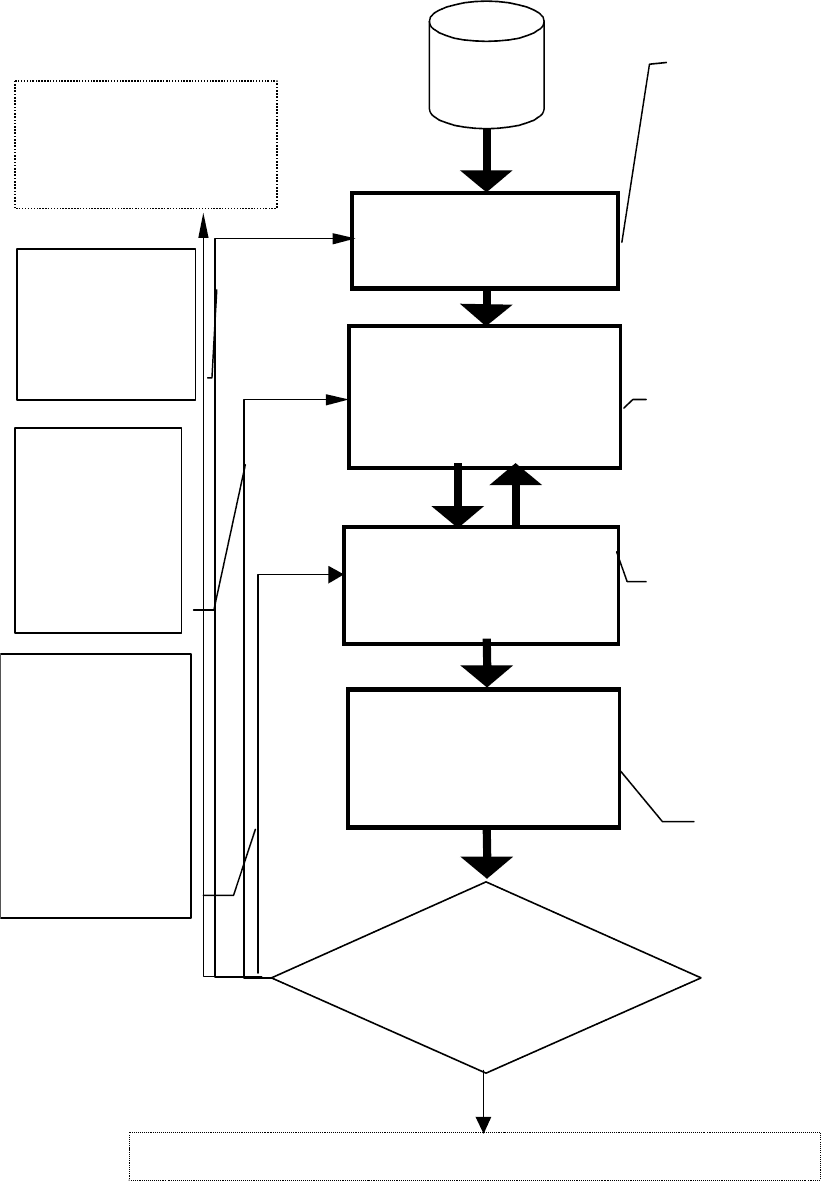
26
формационных систем, существует режим его дообучения в процессе
База
Данных
Предварительная
обработка данных
Выбор
параметров
нейросети
Настройка
(обучение)
нейросети
Оценка
нейросетевой
модели
•
Формирование и
анализ обучающей
выборки
•
Фильтрация
•
Заполнение пробелов
•
Нормировка,
центрирование,
кодирование
•
Выбор структуры НС
•
Выбор вида оценки
•
Выбор характеристики
•
Выбор метода
оптимизации
•
Итеративное обучение
•
Борьба с локальными
минимумами
•
Тестирование
•
Перекрестное
оценивание
•
Изменение
метода
оптимизации
•
Обучение
нескольких
экземпляров
нейросетей
•
Изменение
структуры
модели
•
Изменение
параметров
нейросети
•
Применение
различных
методов
предобработки
Сообщение о
невозможности
построить
нейросетевую модель
Встраивание модели в информационную систему
Модель
удовлетворительна?
НЕТ
ДА
Рис. 4.11. Технология проектирования нейросетевого компонента
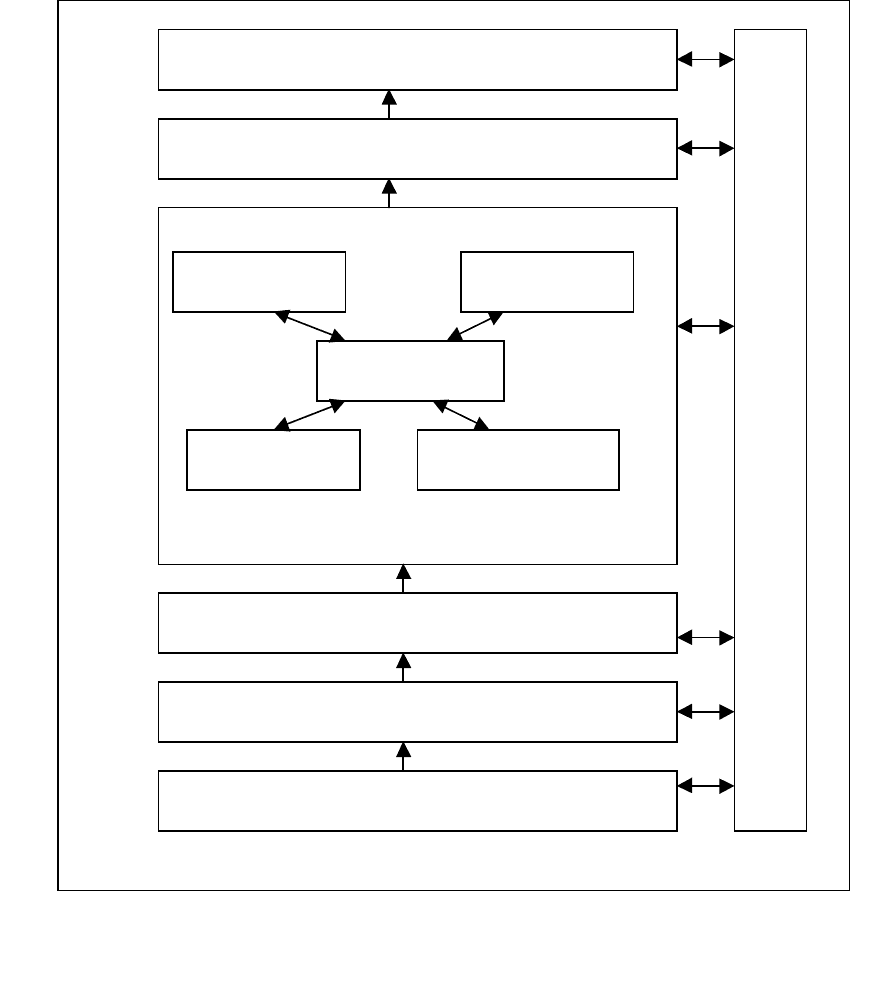
27
Интерпретатор
Нейроимитатор
Сеть
Учитель
Контрастер
Оценка
Конструктор
Менеджер (управляющий модуль)
Интерфейс вывода
Интерфейс ввода
Предобработчик
Задачник
Рис.5.12. Структура нейросетевого интеллектуального блока
эксплуатации на объекте. Особенностью данного режима является то,
что он должен быть незаметен для пользователя, т.е. необходимо постоянное
слежение за состоянием предметной области и его настройка (определение
множества входных параметров, структуры, параметров нейросети, режимов и
методов обучения, автоматический выход из режима останова (удары) ( при не-
корректных обучающих примерах).
28
2.2 Предварительная обработка информации на этапе проектирова-
ния нейросетевых компонентов
Необходимо отметить, что на этапе проектирования информационных
систем нейросетевому моделированию любого экономического процесса или
явления должен предшествовать априорный анализ объекта исследования. Ес-
ли этот этап будет исключен, то, как и при статистическом моделировании,
возможно получение неадекватных действительности результатов на этапе экс-
плуатации модели при функционировании информационной системы. Априор-
ный анализ при нейросетевом моделировании частично отличается от техноло-
гии статистического анализа и состоит из следующих этапов: постановка зада-
чи исследования; обобщение профессиональных знаний об объекте исследова-
ния на основании опыта, интуиции, изучения литературных источников, кон-
сультаций со специалистами и т.п.; формализация полученной априорной ин-
формации об объекте исследования; уточнение и конкретизация постановки за-
дачи, сбор исходных данных, формирование обучающей выборки. Этапы апри-
орного анализа статиcтических данных подробно рассмотрены в литературе
[17,31,100,102].
На этапе предобработки важную роль играет компонент предобработчик
данных. Он занимает место между обучающей выборкой и нейросетью. В него
входят блоки собственно предобработки данных, а также погружения (форми-
рования обучающей выборки) (рис. 4.13). Из литературных источников следу-
ет, что разработка эффективных предобработчиков для нейрокомпьютеров
является новой, почти совсем не исследованной областью [110]. Поэтому дан-
ный раздел при использовании нейросетевого подхода в информационных сис-
темах подлежит существенной доработке. К этапам предобработки данных при
нейросетевом моделировании в информационных системах будем относить:
исключение аномальных наблюдений, проверку однородности данных, запол-
нение пропусков в данных, фильтрацию, нормировку данных, погружение дан-
ных (рис. 4.13). На этапе погружения данных происходит формирование
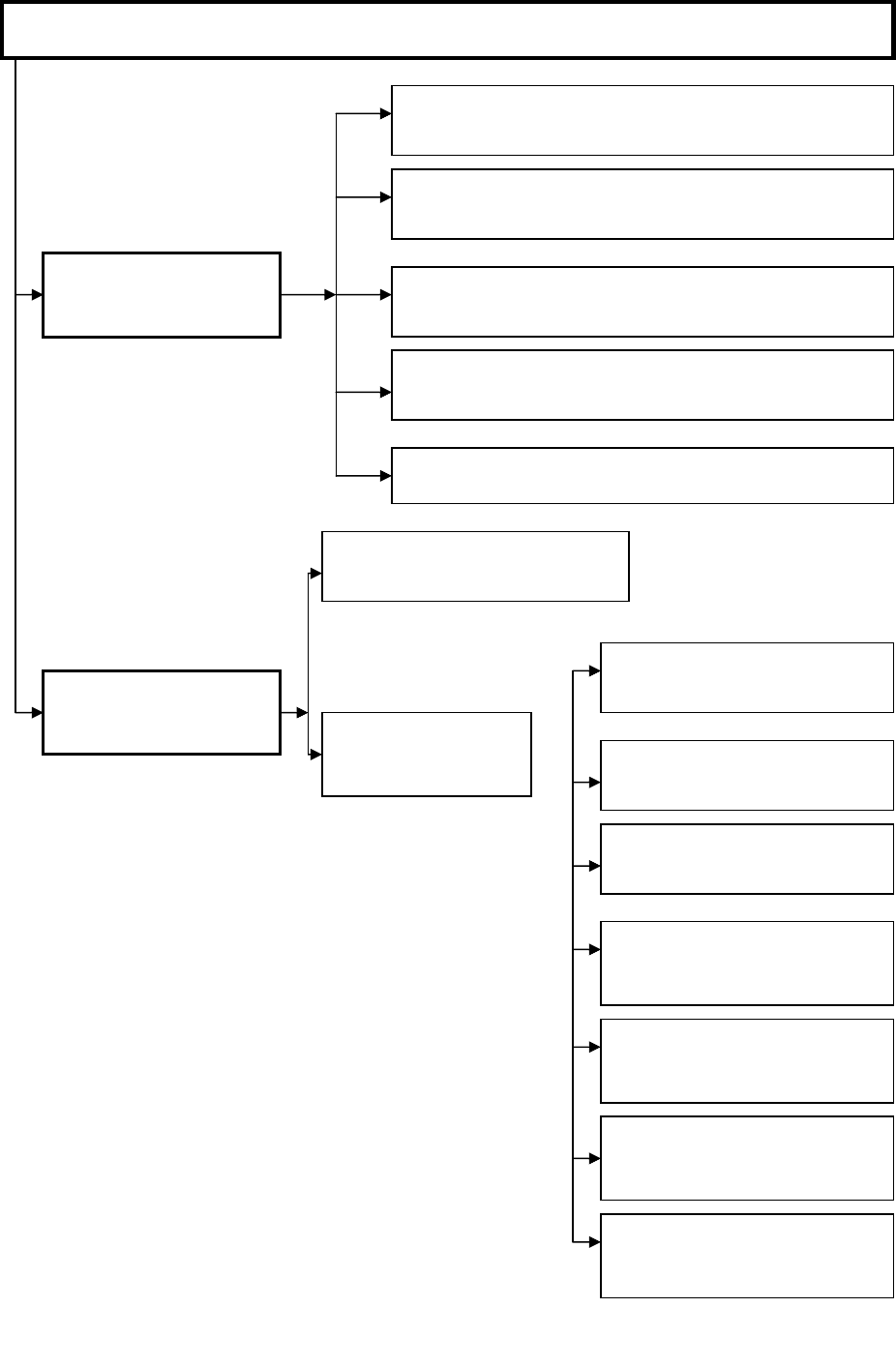
29
Рис. 5.13. Функции предобработчика нейросети
Функции предобработчика нейросети
Предобработка
данных
Погружение
данных
Эвристический анализ данных
Исключение аномальных наблюдений
Заполнение пропусков в данных
Фильтрация данных
Нормализация
Погружение для задач ана-
лиза
Задачи
прогноза
Без пересечения
С пересечением
По одному ряду
По совокупности
временных рядов
С настройкой
глубины погружения
Для режима
"Без дообучения"
Для режима
"С дообучением"
30
обучающей выборки в базе данных в соответствие с определенными пра-
вилами, заданными процедурой решения конкретной прикладной задачи. В ча-
стности, различаются функции погружения при решении задач анализа и про-
гноза. При решении задач прогнозирования выделяются варианты погружения
данных в режимах "без пересечения", "с пересечением", "по одному ряду", "по
совокупности временных рядов"( см. гл.3).
Предварительная очистка и первичная статистическая обработка исход-
ных данных при нейросетевом моделировании включает также этап исключения
аномальных наблюдений. Для этих целей можно применить алгоритмы содер-
жащиеся в работах [17,98], а также алгоритмы «ремонта» данных [184]
Следующим этапом предобработки данных следует считать провер-
ку однородности данных [17]. Исследования показывают, что часто весь ис-
ходный статистический материал, как правило, разбивается на ряд групп, объе-
диненных каким – либо общим признаком. Применение нейросетевой аппрок-
симации по таким данным часто бывает затруднено, сеть учится с перебоями,
так как алгоритмы оптимизации работают не устойчиво. В связи с этим встает
вопрос о сравнении различных групп исходных данных для определения их од-
нородности и установления принадлежности различных выборок единой гене-
ральной совокупности.
Часто при эксплуатации реальных информационных систем неизвест-
на связь обучающей выборки с генеральной совокупностью. Неизвестна связь
выборки с теми или иными законами распределения, корреляционными и рег-
рессионными зависимостями. Поэтому, для проверки однородности выборки
необходимо, прежде всего, обратиться к известной из литературы по распозна-
ванию образов гипотезе компактности [62]. Она утверждает, что реализации
одного и того же образа обычно отображаются в признаковом пространстве в
геометрически близкие точки, образуя «компактные сгустки» . При исследова-
нии компактности (в том числе определения однородности выборки) можно в
качестве предобработки использовать различные меры компактности: среднее
расстояние от центра тяжести до всех точек образа, средней длиной ребра пол-
ного графа или ребра кратчайшего незамкнутого пути, соединяющего точки
одного образа, максимальным расстоянием между двумя точками образа и
т.д.[62]. Кроме того, эффективными являются следующие меры близости объ-
ектов – квадрат евклидова расстояния между векторами значений и признаков,
квадрат расстояния Махаланобиса, квадрат коэффициента корреляции [17]. Для
проверки однородности данных можно применять методы классификации дан-
ных «без учителя»[41]. Наиболее эффективными являются методы динамиче-
ских ядер и нейросетевой метод адаптивной кластеризации данных, основан-
ный на картах Кохонена[41,44,207,233,234].
Важным этапом предобработки является также процедура заполнения
пропусков в данных. Распространенными приемами анализа данных с пропус-
ками являются исключение некомплектных наблюдений (содержащих пропус-
ки хотя бы в одной из переменных) и традиционные методы заполнения про-
