Просолупов Е.В. Конспект курса: Основы дискретной математики

Подождите немного. Документ загружается.

со значением k. Следовательно, в форме распознавания задача не

становится сложнее исходной задачи.

С другой стороны, если решена задача в форме распознавания,

может быть решена задача о нахождении числа цветов в минимальной

раскраске. Для ее решения достаточно перебрать все k от 1 до

n. То есть, сложность задачи нахождения минимального числа

цветов в допустимой раскраске не выше n · T (n), где T (n) — оценка

сложности алгоритма решения задачи в форме распознавания. Эта

задача полиномиально эквивалентна задаче в форме распознавания.

Рассмотрим два класса задач в форме распознавания свойств, — P и

NP , — изучение которых имеет большое значение для теории алгоритмов.

Определение 3.2.7 . Класс P определяется, как класс всех задач

в форме распознавания, для которых существует полиномиальный

алгоритм решения.

Пример 3.2.6 . К классу P , например относятся переформулирован-

ная в форме распознавания свойств задача нахождения минимального

элемента массива:

Дан массив чисел длины n и номер ячейки k. Правда ли, что в

k-той ячейке находится минимальный элемент массива. Сложность

решения этой задачи O(n)

Определение 3.2.8 . Класс NP (от non-deterministic polynomial)

определяется, как класс всех задач в форме распознавания, для которых

существует недетерминированная машина Тьюринга, вычисляющая

ответ на эту задачу за полиномиальное время.

Недетерминированная машина Тьюринга отличается от машин

Тьюринга, с которыми мы сталкивались ранее (детерминированных),

тем, что в ее программе допускается наличие нескольких команд с

одинаковой левой частью. Другими словами, в некоторый момент

времени недетерминированная машина Тьюринга может оказаться в

конфигурации, из которой у нее определено более, чем один вариант

дальнейших действий. Таким образом условие определенности алгоритма

181

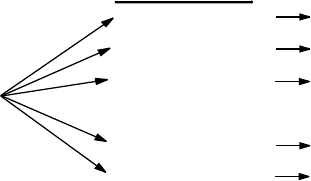
здесь не выполняется. В общем случае у недетерминированного

алгоритма есть целое дерево различных вариантов хода выполнения.

Что делать, если мы столкнулись с такой развилкой? В таком случае

недетерминированная машина может копировать себя необходимое

число раз и все копии начинают выполнять каждая свою возможную

последовательность действий. Копии машины работают независимо и

одновременно (рисунок 30). Как только хотя бы одна копия машины

заканчивает вычисления с ответом "Да", все копии завершают свою

работу. В случае отрицательного ответа, машина может не остановиться.

x x x x x

1 2 3 4 5

0 0 0 00

0 0 0 0

: : :::

1 1 1 1

1 1 1 11

Старт

нет

.....

нет

да

Рисунок 30: Работа недетерминированного алгоритма

Можно также говорить об угадывающем устройстве. Тогда считаем,

что подойдя к развилке машина безошибочно угадывает, какой именно

переход нужно выбрать, чтобы получить ответ "Да", если это возможно.

Определение 3.2.9 . Говорят, что недетерминированная машина

Тьюринга принимает слово α, если существует хотя бы одна ветвь

дерева вычислений, где машина останавливается и дает ответ "Да".

Можно привести альтернативное определение класса NP

Определение 3.2.10 . Задача в форме распознавания принадлежит

классу NP , если, когда на задачу дан ответ "Да" и приведено

доказательство решения — некоторые дополнительные сведения, —

можно за полиномиальное время проверить, что это правда.

182

Пример 3.2.7 . Задача о выполнимости лежит в классе NP .

Действительно, если для некоторой КНФ дан ответ, что она

выполнима, и в подтверждение приведен набор значений аргументов

, x

, ..., x

, то проверить, что значение формулы действительно 1,

можно за полиномиальное время, просто вычислив заданную формой

функцию.

Утверждение 3.2.3 . Определения 3.2.8 и 3.2.10 эквивалентны.

Доказательство. Если задача удовлетворяет определению 3.2.8,

то в качестве доказательства ответа "Да" можно привести номера

веток дерева вариантов выполнения, которые нужно выбирать

недетерминированной машине, чтобы получить ответ за полиномиальное

время.

Пусть задача удовлетворяет определению 3.2.10. Тогда построим

недетерминированную машину, которая в начальный момент времени

создает необходимое число копий и начнет рассмотрение всех возможных

вариантов доказательства правильности ответа. Каждый отдельный

процесс будет проводить проверку доказательства за полиномиальное

время.

Ответы "Да" и "Нет" в случае недетерминированной машины

Тьюринга не симметричны.

Пример 3.2.8 . Рассмотрим задачу о невыполнимости:

Задача 3.2.3 . Дано логическое выражение в конъюнктивной

нормальной форме. Является ли функция, реализуемая этой формулой,

невыполнимой.

Другими словами, дана функция f(x

, x

, ..., x

), определенная своей

КНФ: (D

) ∧ (D

) ∧ · · · ∧ (D

). Требуется ответить на вопрос, правда

ли, что для любых наборов значений логических переменных a

, a

, ...,

, выполняется равенство f(a

, a

, ..., a

) = 0.

Очевидно, что эта задача обратная к задаче о выполнимости,

но она не лежит в классе NP , поскольку для нее не может

существовать недетерминированного полиномиального алгоритма

183

решения: в любом случае, чтобы получить положительный ответ

на данную задачу, мы должны проверить все возможные наборы

логических переменных, а сложность этого процесса имеет порядок

O(2

). Недетерминированность в данном случае не может улучшить

ситуацию.

Действительно, если даже машина копирует себя 2

раз и каждая

копия проверяет свой набор аргументов функции, ни одна копия

не сможет узнать, какой ответ получили оставные, и значит не

сможет дать положительный ответ на задачу.

Если же нам дан ответ "Да", то мы не сможем предоставить

доказательство этого ответа, которое можно было бы проверить за

полиномиальное время. В любом случае нам придется проверить все 2

наборов аргументов, чтобы убедиться в правильности ответа.

3.2.4 Отношение между классами P и NP

Ясно, что недетерминированная машина Тьюринга является частным

случаем детерминированной, так что P ⊆ NP . Более полную систему

отношений между классами задач в форме распознавания можно увидеть

на рисунке 31.

Кажется, что NP 6= P , поскольку недетерминированная машина

может выполнять несколько процессов одновременно, при условии, что

хотя бы один из них остановится и выдаст положительный результат.

С другой стороны, с помощью детерминированной машины Тьюринга

можно смоделировать работу недетерминированной машины, используя

дополнительные состояния, когда встречается неоднозначность, подобно

тому, как это делают псевдомногозадачные операционные системы.

Работа такой моделирующей машины требует значительно большего

времени, чем работа оригинальной недетерминированной машины

Тьюринга, но не известно на сколько больше — сохранит ли полученный

алгоритм свойство полиномиальности.

Вопрос о том, найдется ли для любой задачи из класса NP

эффективный алгоритм решения является классическим вопросом о

равенстве классов P и NP , который уже много лет остается одной из

центральных открытых научных проблем. Вопрос равенства классов

184

NP-полные

Задачивформе

распознавания

Рисунок 31: Отношение между классами задач в форме распознавания.

NP и P по сути состоит в следующем: если положительный ответ на

задачу можно проверить за полиномиальное вермя, то правда ли, что этот

ответ можно также за полиномиальное время и найти. Действительно ли

задачи легче проверить, чем решить?

Если бы было доказано, что P = NP , это позволило бы решить це-

лый ряд задач, для которых до сих пор не известно полиномиальных

алгоритмов решения. Большое количество классических задач лежит

в классе NP . В то же время, это могло бы повлечь и проблемы,

связанные, например, с ненадежностью (в этом случае) некоторых

алгоритмов шифрования, основанных на предполагаемой невозможности

быстро проводить определенные вычисления.

В настоящее время большинство математиков считает, что эти классы

не равны, но доказательство остается ненайденым.

3.2.5 NP -полные задачи

Следующая теорема была доказана Куком в 1971 году.

185

Теорема 3.2.4 . Любая задача из класса NP полиномиально сводится

к задаче о выполнимости.

Таким образом, задача о выполнимости в некотором смысле не проще

всех остальных задач из класса NP . Все подобные ей задачи названы

NP -полными.

Определение 3.2.11 . Задача называется NP -полной, если она

принадлежит классу NP и к ней полиномиально сводятся все задачи

из класса NP .

Замечание 3.2.4 . Все NP -полные задачи попарно полиномиально

эквивалентны.

Определение 3.2.12 . Задача называется NP -трудной, если к ней

полиномиально сводятся все задачи из класса NP .

Пример 3.2.9 . Можно доказать, что задача о раскраске контур-

ной карты из примера 3.2.5 в оптимизационной форме является

NP -трудной, а ее переформулировка в форме распознавания свойств яв-

ляется NP -полной задачей.

Теперь для доказательства NP -полноты задачи из класса NP доста-

точно показать, что к ней полиномиально сводится некоторая известная

NP -полная задача.

Пример 3.2.10 . Из теоремы 3.2.1 следует, что и задача о 3-выпол-

нимости также является NP -полной.

Можно заметить, что задача о 2-выполнимости лежит в классе P.

Понятие NP -полной задачи может помочь прояснить ситуацию с

отношением между классами P и NP . Если будет найден полино-

миальный алгоритм решения одной из NP -полных задач, то любая

задача из класса NP сможет быть решена за полиномиальное время и,

следовательно, P = NP .

Если для произвольной задачи из класса NP будет доказано, что она

за полиномиаьное время не решается, то окажется верно, что P 6= NP и

любая NP -полная задача не сможет лежать в P .

186

На практике полезно уметь распознавать NP -полные задачи. Если

будет доказано, что рассматриваемая вами задача NP -полна, то

нахождение полиномиального алгоритма решения этой задачи будет

равносильно решению вопроса о равенстве или неравенстве классов P и

NP , который остается без ответа уже более тридцати лет. С практической

точки зрения такие задачи можно считать неразрешимыми эффективно

и искать приближенные алгоритмы их решения.

187

Литература

[1] Нефедов В.Н., Осипова В.А. Курс дискретной математики. М.: Изд-во

МАИ, 1992.

[2] Грэхэм Р., Кнут Д., Паташник О. Конкретная математика. М.: Мир,

1998.

[3] Романовский И.В. Дискретный анализ. СПб.: Невский диалект, 2000.

[4] Яблонский С.В. Введение в дискретную математику. М.: Наука, 1979.

[5] Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной

математике. 1977. 367 с.

[6] Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной

математике. — М.: Физматлит, 2004.

[7] Лавров И.А., Максимова Л.Л. Задачи по теории множеств,

математической логике и теории алгоритмов. — М.: Физматлит, 1995.

[8] Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые

задачи. М.:Мир, 1982.

188