Просолупов Е.В. Конспект курса: Основы дискретной математики

Подождите немного. Документ загружается.

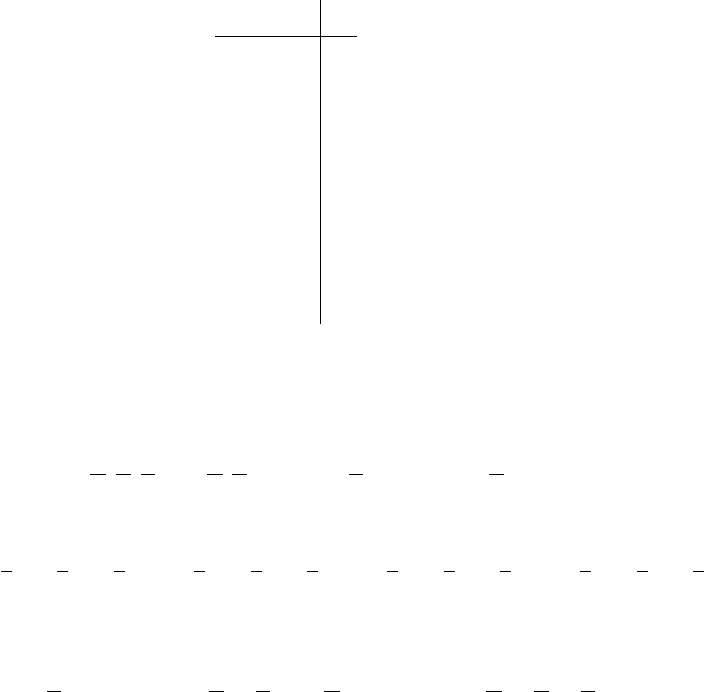
для функции f 6= 1.

Теперь для построения СДНФ согласно формуле (28) необходимо

выбрать каждый набор (σ

, ..., σ

), для которого f(σ

, ..., σ

) = 1,

и сопоставить ему коньюнкт x

· · · x

совершенной дизъюнктивной

нормальной формы.

Аналогично строится совершенная конъюнктивная нормальная

форма по формуле (29).

Пример 2.1.11 . Рассмотрим функцию f(x, y, z), заданную таблицей:

x y z f

0 0 0 1

0 0 1 1

0 1 0 0

0 1 1 0

1 0 0 0

1 0 1 1

1 1 0 1

1 1 1 0

Тогда, согласно (28) СДНФ будет выглядеть следующим образом:

f(x, y, z) = x

∨ x

= x y z ∨ x y z ∨ x y z ∨ x y z.

СКНФ согласно формуле (29) будет иметь вид:

f(x, y, z) = (x

∨ y

∨ z

) ∧ (x

∨ y

∨ z

) ∧ (x

∨ y

∨ z

) ∧ (x

∨ y

∨ z

) =

∨ y

∨ z

) ∧ (x

∨ y

∨ z

) ∧ (x

∨ y

∨ z

) ∧ (x

∨ y

∨ z

) =

= (x ∨ y ∨ z) ∧ (x ∨ y ∨ z) ∧ (x ∨ y ∨ z) ∧ (x ∨ y ∨ z).

2.1.6 Полином Жегалкина

Рассмотрим еще одно представление функции в виде формулы заданного

вида.

101

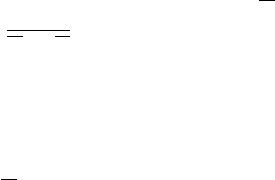
Определение 2.1.13 . Формула вида

⊕ α

⊕ ... ⊕ α

⊕ α

⊕ ... ⊕ α

12...n

...x

, (30)

где x

, ..., x

— логические переменные, а α

, α

, ..., α

12...n

— логические

константы, называется полиномом Жегалкина.

Замечание 2.1.9 . Для удобства будем также использовать

следующую запись:

I⊆{1,...,n}

α(I)

i∈I

Пример 2.1.12 .

1 ⊕ x

⊕ x

— полином Жегалкина.

Здесь n = 3, α

= α

= 1, а α

= α

123

= 0.

Утверждение 2.1.6 . Пусть f(x

, ..., x

) ∈ P

. Тогда фукнция

f может быть представлена полиномом Жегалкина, причем

единственным образом.

Доказательство. Для начала докажем существование такого

представления для функции. Прежде всего заметим, что произвольная

функция представима в виде формулы U

над {¬, ∨, ∧}: если f 6= 0, ее

можно представить в виде СДНФ, а f = 0 представим как f = x ∧ x.

Воспользуемся законом де Моргана x ∨ y = x ∧ y и заменим все

дизъюнкции в формуле U

на конъюнкции и отрицание. Получим

представление функции f(x

, ..., x

) в виде формулы U

над системой

элементарных функций {¬, ∧}. Заменим в формуле U

все отрицания

на сложение по модулю два согласно тождеству x = 1 ⊕ x . Раскроем

все скобки, пользуясь дистрибутивностью ∧ относительно ⊕, и получим

формулу вида (30).

Теперь докажем единственность. Пусть

f(x

, ..., x

) =

I⊆{1,...,n}

α(I)

i∈I

I⊆{1,...,n}

β(I)

i∈I

— два различных полинома Жегалкина для фукнции f. Полиномы

различны, когда отличаются наборы их коэффициентов α и β.

102

Выберем I

∗

⊆ {1, ..., n} такой, что α(I

∗

) 6= β(I

∗

) и α(I) = β(I) для

любого I ⊂ I

∗

. Мы можем выбрать такой набор, начав с I

= {1, ..., n}

и последовательно удаляя индексы, для которых указанное свойство не

выполняется. Так, если для набора индексов I

существует j ∈ I

α(I

\ j) 6= β(I

\ j), то выбираем I

k+1

= I

\ j и так далее, пока не

получим I

с искомыми свойствами.

Пусть

1, i ∈ I

∗

0, i /∈ I

∗

i = 1, n.

Тогда

f(σ

, ..., σ

) =

I⊆{1,...,n}

α(I)

i∈I

I⊆I

∗

α(I) =

I⊂I

∗

α(I) ⊕ α(I

∗

)

и в то же время

f(σ

, ..., σ

) =

I⊆{1,...,n}

β(I)

i∈I

I⊆I

∗

β(I) =

I⊂I

∗

β(I) ⊕ β(I

∗

Таким образом,

I⊂I

∗

α(I) ⊕ α(I

∗

) =

I⊂I

∗

β(I) ⊕ β(I

∗

) =⇒ α(I

∗

) = β(I

∗

Противоречие с нашим исходным предположением о I

∗

доказывает

утверждение.

Замечание 2.1.10 . Полином Жегалкина является формулой над

{0, 1, ∧, ⊕}. 0 нам требуется для задания тождественно нулевой

функции. Для остальных случаев нам будет достаточно функций

1, ∧, ⊕.

Пример 2.1.13 . Рассмотрим функцию f, заданную формулой

f(x, y, z) = xy ⊃ z ∨ xy. Представим ее с помощью формулы над {¬, ∧}.

xy ⊃ z = xy ∨ z = xy ∧ z,

xy ⊃ z ∨ xy = (xy ⊃ z) ∧ xy = xy ∧ z ∧ xy

103

Теперь избавимся от отрицаний и раскроем скобки.

xy ∧ z ∧ xy = 1 ⊕ ((1 ⊕ (xy ∧ (1 ⊕ z))) ∧ (1 ⊕ xy)) =

= 1 ⊕ 1 ⊕ xy ⊕ (xy ∧ (1 ⊕ z)) ⊕ (xy ∧ (1 ⊕ z))xy =

= xy ⊕ (xy ∧ (1 ⊕ z)) ⊕ (xy ∧ (1 ⊕ z)) = xy.

Таким образом, единственным ненулевым коэффициентом полинома

Жегалкина для функции f оказался α

и сам полином имеет вид

f(x, y, z) = xy.

Замечание 2.1.11 . Для построения полинома Жегалкина есть

и более удобный способ — метод неопределенных коэффициентов.

Предположим, что функция f(x

, ..., x

) задана таблицей значений

для всех наборов аргументов. Нам известен общий вид полинома

Жегалкина для f

I⊆{1,...,n}

α(I)

i∈I

и требуется только вычислить коэффициенты α(I).

Проходя по всей таблице значений для f будем приравнивать общий

вид полинома и известное значение функции на данном наборе, тем

самым последовательно вычисляя коэффициенты α.

f(0, ..., 0) =

I⊆{1,...,n}

α(I)

i∈I

0 = α(∅). Отсюда имеем первый

коэффициент:

α(∅) = f(0, ..., 0).

f(0, .., 0, 1) = α(∅) ⊕ α({n}) ∧ 1. Таким образом,

α({n}) = f(0, ..., 0, 1) ⊕ α(∅) = f(0, ..., 0, 1) ⊕ f(0, ..., 0, 0).

f(0, ..., 0, 1, 0) = α(∅) ⊕ α ({n − 1}) ∧ 1 и

α({n − 1}) = f(0, ..., 0, 1, 0) ⊕ α(∅) = f(0, ..., 0, 1, 0) ⊕ f(0, ..., 0, 0, 0).

f(0, ..., 0, 1, 1) = α(∅) ⊕ α ({n − 1}) ⊕ α({n}) ⊕ α({n − 1, n}) и,

следовательно,

α({n − 1, n}) = f(0, ..., 0, 1 , 1) ⊕ α(∅) ⊕ α({n − 1}) ⊕ α({n}) =

104

= f(0, ..., 0, 1, 1) ⊕ f(0, ..., 0, 0, 0) ⊕ f(0, ..., 0, 1, 0)⊕

⊕f(0, ..., 0, 0, 0) ⊕ f(0, ..., 0, 1) ⊕ f(0, ..., 0, 0) =

= f(0, ..., 0, 1, 1) ⊕ f(0, ..., 0, 1, 0) ⊕ f(0, ..., 0, 0, 1) ⊕ f(0, ..., 0, 0, 0)

Продолжая этот процесс мы сможем вычислить все коэффициенты

и тем самым получим полином Жегалкина для функции f.

Пример 2.1.14 . Построим полином Жегалкина для функции

f(x, y, z) = xy ⊃ z ∨ xy из примера 2.1.13 с помощью метода

неопределенных коэффициентов. В общем виде полином для функции

от трех переменных выглядит следующим образом:

f(x, y, z) = α

⊕ α

x ⊕ α

y ⊕ α

z ⊕ α

1,2

xy ⊕ α

1,3

xz ⊕ α

2,3

yz ⊕ α

1,2,3

xyz.

Переберем все возможные наборы аргументов.

f(0, 0, 0) = 0 = α

⇒ α

= 0,

f(0, 0, 1) = 0 = α

⊕ α

⇒ α

= 0,

f(0, 1, 0) = 0 = α

⊕ α

⇒ α

= 0,

f(0, 1, 1) = 0 = α

⊕ α

2,3

⇒ α

2,3

= 0,

f(1, 0, 0) = 0 = α

⊕ α

⇒ α

= 0,

f(1, 0, 1) = 0 = α

⊕ α

1,3

⇒ α

1,3

= 0,

f(1, 1, 0) = 1 = α

⊕ α

1,2

⇒ α

1,2

= 1,

f(1, 1, 1) = 1 = α

⊕ α

1,2

⊕

⊕α

1,3

⊕ α

2,3

⊕ α

1,2,3

⇒ α

1,2,3

= 0.

Полином Жегалкина имеет вид f(x, y, z) = xy, что совпадает с

результатом примера 2.1.13.

Пример 2.1.15 . Рассмотрим еще один пример использования метода

неопределенных коэффициентов. Пусть f(x, y, z) = (x ⊕ y) ⊃ z. Пусть

105

f(x, y, z) = xy ∨ xz ∨ yz.

f(0, 0, 0) = 0 = α

⇒ α

= 0,

f(0, 0, 1) = 0 = α

⊕ α

⇒ α

= 0,

f(0, 1, 0) = 0 = α

⊕ α

⇒ α

= 0,

f(0, 1, 1) = 1 = α

⊕ α

2,3

⇒ α

2,3

= 1,

f(1, 0, 0) = 0 = α

⊕ α

⇒ α

= 0,

f(1, 0, 1) = 1 = α

⊕ α

1,3

⇒ α

1,3

= 1,

f(1, 1, 0) = 1 = α

⊕ α

1,2

⇒ α

1,2

= 1,

f(1, 1, 1) = 1 = α

⊕ α

1,2

⊕

⊕α

1,3

⊕ α

2,3

⊕ α

1,2,3

⇒ α

1,2,3

= 0.

Следовательно, полином Жегалкина для функции f будет иметь вид

f(x, y, z) = xy ⊕ xz ⊕ yz.

2.1.7 Полнота системы функций

Определение 2.1.14 . Система функций P ⊆ P

называется полной,

если любую функцию из P

можно представить в виде формулы над P.

Замечание 2.1.12 . Удобно доказывать полноту системы функций,

показывая, что она сводится к уже известной полной системе.

Лемма 2.1.7 . Пусть, даны две системы функцй P ⊆ P

и Q ⊆ P

Пусть функция f(x

, x

, ..., x

) представима в виде формулы над P, и

любая функция из P представима в виде формулы над Q. Тогда функция

f представима в виде формулы над Q.

Доказательство. Пусть, U — формула над P, реализующая функцию

f. U

, U

, ..., U

— формулы над Q, реализующие все функции g

, g

..., g

множества P. Тогда каждое вхождение функции g

в формулу U

можно заменить формулой U

. Проведя такую замену, получим формулу

над Q. Очевидно, формула U

эквивалентна формуле U, поскольку

они отличаются заменой подформул на эквивалентные.

Теорема 2.1.8 . Пусть, даны две системы функцй P ⊆ P

и Q ⊆ P

Пусть P — полная система функций, и любая функция из P предста-

вима в виде формулы над Q. Тогда, Q — полная система функций.

106

Доказательство. Непосредственно следует из леммы 2.1.7.

Приведем несколько примеров полных систем функций.

Утверждение 2.1.9 . {¬, ∨, ∧} — полная система функций.

Доказательство. Рассмотрим произвольную функцию f ∈ P

Если f = 0, то f = f

, где U = x ∧ x.

В противном случае f 6= 0. Тогда по утверждению 2.1.3 f = f

, где

U =

(σ

,...,σ

)

f(σ

,...,σ

)=1

· · · x

Следствие 2.1.10 . {¬, ∧} и {¬, ∨} — полные системы функций.

Доказательство. Докозательство очевидно следует из утверждения

2.1.9 и правил де Моргана, если заметить, что

x ∨ y = x ∧ y, и x ∧ y = x ∨ y.

Таким образом, подставив в любую формулу, выражающую функцию f в

виде формулы над {¬, ∨, ∧}, указанные выражения для ∨ или ∧, можно

получить эквивалентную формулу над {¬, ∧} или над {¬, ∨}.

Утверждение 2.1.11 . 1) Системы функций {|} и {↓} — полные

системы функций.

2) Других полных систем, состоящих из одной функции от двух

переменных нет.

Доказательство. 1) а) x = x | x, x ∨ y = x | y = (x | x) | (y | y).

б) x = x ↓ x, x ∧ y = x ↓ y = (x ↓ x) ↓ (y ↓ y).

2) Пусть h(x, y) ∈ P

и {h} — полная система функций.

Пусть h(0, 0) = 0. Тогда, если f(x) задна в виде формулы над {h},

то f(0) = 0. Действительно, функция f имеет вид f(x) = h(U

, U

), где

— переменная x, или формула того же вида, что и f, i = 1, 2. Таким

образом, в конце концов оказывается, что f(0) = h(0, 0) = 0. Тогда,

с помощью только функции h(x, y) не может быть функция отрицания,

поскольку ¬0 = 1. Следовательно h(0, 0) = 1.

107

Аналогично можно показать, что h(1, 1) = 0.

Теперь рассмотрим все функции от двух переменных,

удовлетворяющие полученному условию: h(0, 0) = 1, h(1, 1) = 0.

Всего таких функций четыре (Скажите почему).

x y ↓ | x y

0 0 1 1 1 1

0 1 0 1 1 0

1 0 0 1 0 1

1 1 0 0 0 0

Как видно из таблицы, две из этих функций известны нам как

стрелка Пирса и штрих Шеффера, а две другие представляют из себя

функцию отрицания от аргументов x и y. Поскольку система из одной

функции отрицания не является полной системой функций, утверждение

доказано.

Утверждение 2.1.12 . {0, 1, ⊕, ∧} — полная система функций.

Доказательство. Истинность этого утверждения следует из того, что

любая функция из P

представима в виде полинома Жегалкина (утв.

2.1.6).

Следствие 2.1.13 . Так как 1 ⊕ 1 = 0, полной системой функций

является и {1, ⊕, ∧}.

Определение 2.1.15 . Пусть

= {f

, ..., x

), f

, ..., x

), ..., f

, ..., x

)}.

f — суперпозиция ранга 1 (элементарная суперпозиция) функций f

, ...,

, если f получена одним из способов:

a) переименованием некоторой переменной x

функции f

i ∈ {1, ..., m}, j ∈ {1, ..., k

, ..., x

j−1

, y, x

j+1

, ..., x

108

где y может совпасть с любой переменной;

b) подстановкой некоторой функции f

вместо переменной x

функции f

, l, i ∈ {1, ..., m}, j ∈ {1, ..., k

, ..., x

j−1

, f

, ..., x

), x

j+1

, ..., x

Множество суперпозиций ранга 1 функций из K

обозначим

. Также, множество суперпозиций ранга 1 функций из K

i−1

обозначим K

, i = 1, ∞. Функции из множества K

будем называть

суперпозициями ранга i функций из K

Определение 2.1.16 . Суперпозицией функций из K

будем называть

суперпозицию любого ранга. Другими словами, f — суперпозиция

функций f

, ..., f

, если ∃t ∈ N такое, что f ∈ K

Замечание 2.1.13 . По сути дела утверждение, что f является

суперпозицией функций из K

, эквивалентно утверждению, что f

представима в виде формулы над K

. Таким образом мы можем

переформулировать определение полной системы.

Определение 2.1.17 (2.1.14’). Система функций P ⊆ P

называется полной, если любая функция из P

является суперпозицией

функций из P.

Определение 2.1.18 . Пусть M ⊆ P

. Замыканием M называется

множество

[M] = {f | f — суперпозиция функций из M}.

Определение 2.1.19 . Пусть M ⊆ P

. M — замкнутое множество

функций, если M = [M].

Пример 2.1.16 .

1) M = {x, x}. Тогда [M] = {x, x} = M и M — замкнуто.

2) M = {x}. Тогда [M] = {x, x} 6= M. Множество M — не

замкнуто.

Несложно проверить нижеследующие свойства операции замыкания.

109

Утверждение 2.1.14 . Пусть M, N ⊂ P

1) Замыкание множества содержит само множество:

M ⊆ [M].

2) Замыкание произвольного множества замкнуто:

[[M]] = [M].

3) Замыкание сохраняет включение множеств:

M ⊆ N ⇒ [M] ⊆ [N].

4) Замыкание объединения содержит объединение замыканий:

[M] ∪ [N] ⊆ [M ∪ N].

Замечание 2.1.14 . Заметим,что для доказательства замкнутости

некоторого класса функций M достаточно показать, что любая

суперпозиция ранга 1 функций из M лежит в M.

Обозначим множество суперпозиций ранга i функций из M за M

Пусть M

= M. Тогда M

— множество суперпозиций ранга 1 функций

из M

= M. Следовательно, M

= M

= M. Аналогично можно

убедиться, что M

= M, i = 1, ∞.

Далее, когда мы будем доказывать замкнутость классов функций,

будем ограничиваться только рассмотрением суперпозиций ранга 1.

С учетом определения замкнутости можно дать еще одно

альтернативное определение полноты.

Определение 2.1.20 (2.1.14”). Система функций P ⊆ P

— полная,

если [P] = P

Далее мы бы хотели доказать критерий, позволяющий для

произвольной системы функций из P

определить, является ли она

полной. Для этого нам понадобится ввести и изучить свойства нескольких

замкнутых классов функций алгебры логики.

110