Principles of Finance with Excel (Основы финансов c Excel)

Подождите немного. Документ загружается.

PFE Chapter 1, Time value of money page 40

As in the first example of this section, the IRR is the rate of return on the investment—

defined as the rate that repays, over the life of the asset, the initial investment in the asset and

that pays interest on the outstanding investment balances.

Using future value, net present value, and internal rate of return—several problems

In the remaining sections we apply the concepts learned in the chapter to solve several common

problems:

1.7 and 1.8. Saving for the future

1.9. Paying off a loan with “flat” payments of interest and principal

1.10. How long does it take to pay off a loan?

1.7. Saving for the future—buying a car for Mario

Mario wants to buy a car in 2 years. He wants to open a bank account and to deposit $X

today and $X in one year. Balances in the account will earn 8%. How much should Mario

deposit so that he has $20,000 in 2 years? In this section we’ll show you that:

In order to finance future consumption with a savings plan, the net present value of all

the cash flows has to be zero. In the jargon of finance—the future consumption plan is

fully funded

if the net present value of all the cash flows is zero.

In order to see this, start with a graphical representation of what happens:

012

X X -20,000

X*(1.08)

PFE Chapter 1, Time value of money page 41

In year 2 Mario will have accumulated

(

)

(

)

*1.08 *1.08XX+ . This should finance the $20,000

car, so that:

() ()

Desired accumulation

Future value of

deposits in 2 years

* 1.08 * 1.08 20,000XX

↑





Now subtract the $20,000 from both sides of the equation and divide through by

()

1.08

()

Net present value

of all cash flows

20,000

1.08

↑

+− =



We’ve proved it—in order to fully fund Mario’s future purchase of the car, the net

present value of all the payments has to be zero.

Excel solution

Of course, we won’t leave it at this—we’ll show you Mario’s problem in Excel:

ABCDE

Deposit, X 8,903.13

Interest rate 8.00%

Year

In bank, before

deposit

Deposit or

withdrawal

Total at

beginning of

year

End of year

with interest

0 0.00 8,903.13 8,903.13 9,615.38

1 9,615.38 8,903.13 18,518.52 20,000.00

2 20,000.00 (20,000.00) 0.00 0.00

NPV of all

deposits

and payments

$0.00 <-- =C5+NPV(B3,C6:C7)

HELPING MARIO SAVE FOR A CAR

If he deposits $8,903.13 in years 0 and 1, then the accumulation in the account at the

beginning of year 2 will be exactly $20,000 (cell B7). The NPV of all the payments (cell C9) is

zero.

PFE Chapter 1, Time value of money page 42

How did we actually arrive at $8,903.13? We’ll postpone this to the next section, where

we discuss a somewhat more complicated and realistic version of the same problem.

1.8. Saving for the future—more realistic problems

In this section we present more complicated versions of Mario’s problem from section

1.7. We start by trying to determine whether a young girl’s parents are putting enough money

aside to save for her college education. Here’s the problem:

•

On her tenth birthday Linda Jones’s parents decide to deposit $4,000 in a savings account

for their daughter. They intend to put an additional $4,000 in the account each year on

her 11

, 12

, ..., 17

birthdays.

•

All account balances will earn 8% per year.

•

On Linda’s 18

, 19

, 20

, and 21

birthdays, her parents will withdraw $20,000 to pay

for Linda’s college education.

Is the $4,000 per year sufficient to cover the anticipated college expenses? We can easily

solve this problem in a spreadsheet:

PFE Chapter 1, Time value of money page 43

ABCDE

Interest rate 8%

Annual deposit 4,000.00

Annual cost of college 20,000

Birthday

In bank on birthday,

before

deposit/withdrawal

Deposit

or withdrawal

at begin. of year

Total

End of year

with interest

10 0.00 4,000.00 4,000.00 4,320.00

11 4,320.00 4,000.00 8,320.00 8,985.60

12 8,985.60 4,000.00 12,985.60 14,024.45

13 14,024.45 4,000.00 18,024.45 19,466.40

14 19,466.40 4,000.00 23,466.40 25,343.72

15 25,343.72 4,000.00 29,343.72 31,691.21

16 31,691.21 4,000.00 35,691.21 38,546.51

17 38,546.51 4,000.00 42,546.51 45,950.23

18 45,950.23 -20,000.00 25,950.23 28,026.25

19 28,026.25 -20,000.00 8,026.25 8,668.35

20 8,668.35 -20,000.00 -11,331.65 -12,238.18

21 -12,238.18 -20,000.00 -32,238.18 -34,817.24

NPV of all payments -13,826.4037 <-- =NPV(B2,C8:C18)+C7

SAVING FOR COLLEGE

By looking at the end-year balances in column E, the $4,000 is not enough—Linda and

her parents will run out of money somewhere between her 19

and 20

birthdays.

By the end of

her college career, they will be $34,817 “in the hole.” Another way to see this is to look at the

net present value calculation in cell C20: As we saw in the previous section, a combination

savings/withdrawal plan is fully funded when the NPV of all the payments/withdrawals is zero.

In cell C20 we see that the NPV is negative—Linda’s plan is underfunded.

How much should Linda’s parents put aside each year? There are several ways to answer

this question, which we explore below.

At the end of Linda’s 19 year (row 16), there is $8,668.35 remaining in the account. At the end of the following

year, there is a negative amount in the account.

PFE Chapter 1, Time value of money page 44

Method 1: Trial and error

Assuming that you have written the spreadsheet correctly, you can “play” with cell B3

until cell E18 or cell C20 equals zero. Doing this shows that Linda’s parents should have

planned to deposit $6,227.78 annually:

ABCDE

Interest rate 8%

Annual deposit 6,227.78

Annual cost of college 20,000

Birthday

In bank on birthday,

before

deposit/withdrawal

Deposit

or withdrawal

at begin. of year

Total

End of year

with interest

10 0.00 6,227.78 6,227.78 6,726.00

11 6,726.00 6,227.78 12,953.77 13,990.08

12 13,990.08 6,227.78 20,217.85 21,835.28

13 21,835.28 6,227.78 28,063.06 30,308.10

14 30,308.10 6,227.78 36,535.88 39,458.75

15 39,458.75 6,227.78 45,686.52 49,341.45

16 49,341.45 6,227.78 55,569.22 60,014.76

17 60,014.76 6,227.78 66,242.54 71,541.94

18 71,541.94 -20,000.00 51,541.94 55,665.29

19 55,665.29 -20,000.00 35,665.29 38,518.52

20 38,518.52 -20,000.00 18,518.52 20,000.00

21 20,000.00 -20,000.00 0.00 0.00

NPV of all payments 0.0000 <-- =NPV(B2,C8:C18)+C7

SAVING FOR COLLEGE

Notice that the net present value of all the payments (cell C20) is zero when the solution

is reached. The future payouts are fully funded when the NPV of all the cash flows is zero.

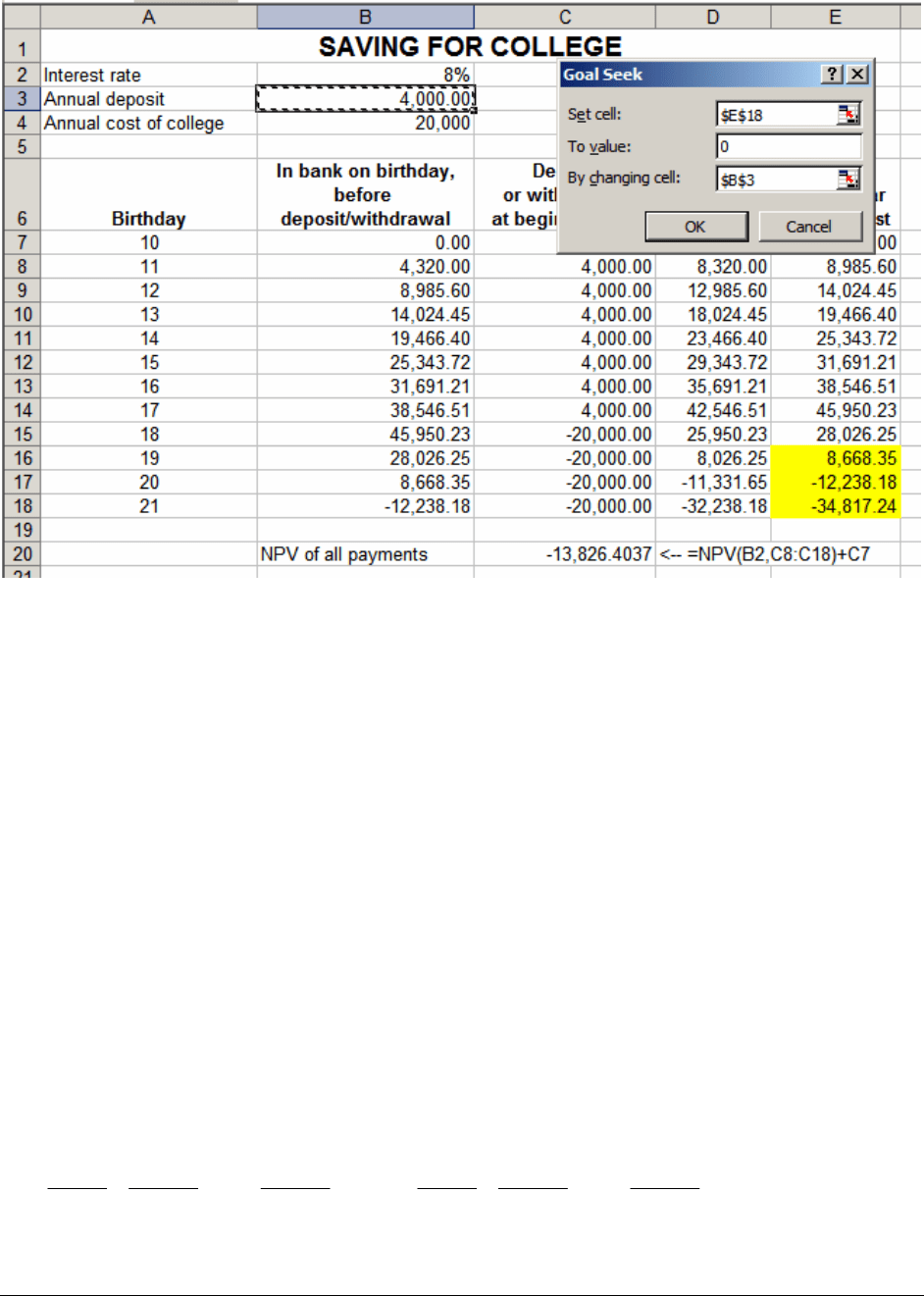
Method 2: Using Excel’s Goal Seek

Goal Seek is an Excel function that looks for a specific number in one cell by adjusting

the value of a different cell (for a discussion of how to use

Goal Seek, see Chapter 000). To

solve our problem of how much to save, we can use

Goal Seek to set E18 equal to zero. After

hitting

Tools|Goal Seek, we fill in the dialog box:

PFE Chapter 1, Time value of money page 45

When we hit “OK,” Goal Seek looks for the solution. The result is the same as before:

$6,227.78.

Method 3: Using the Excel NPV formula

The method in this subsection involves the most preparation. Its advantage is that it leads

to a very compact solution to the problem—a solution that doesn’t require a long Excel table for

its implementation. On the other hand, the formulas required are somewhat intricate (if you

really hate formulas, skip this method!).

Linda’s parents are going to make 8 deposits of $X each, starting today. The present

value of these deposits is

()

() ()

()

() ()

27 27

11 1

1.08 1.08

1.08 1.08 1.08 1.08

XX X

⎛⎞

⎜⎟

++ ++ =++ ++

⎜⎟

⎝⎠

……

PFE Chapter 1, Time value of money page 46

The account created will then have 4 withdrawals of $20,000, starting in year 8. The present

value of these withdrawals is:

()()()()

()

()()()

8 9 10 11 2 3 4

20,000 20,000 20,000 20,000 20,000 1 1 1 1

1.08 1.08

1.08 1.08 1.08 1.08 1.08 1.08 1.08

⎛⎞

⎜⎟

++ + = +++

⎜⎟

⎝⎠

Setting these two equations equal allows us to solve for X:

()

()()()

()

() ()

234

20,000 1 1 1 1

1.08 1.08

1.08 1.08 1.08

11 1

1.08

1.08 1.08

⎛⎞

⎜⎟

+++

⎜⎟

⎝⎠

++ ++

…

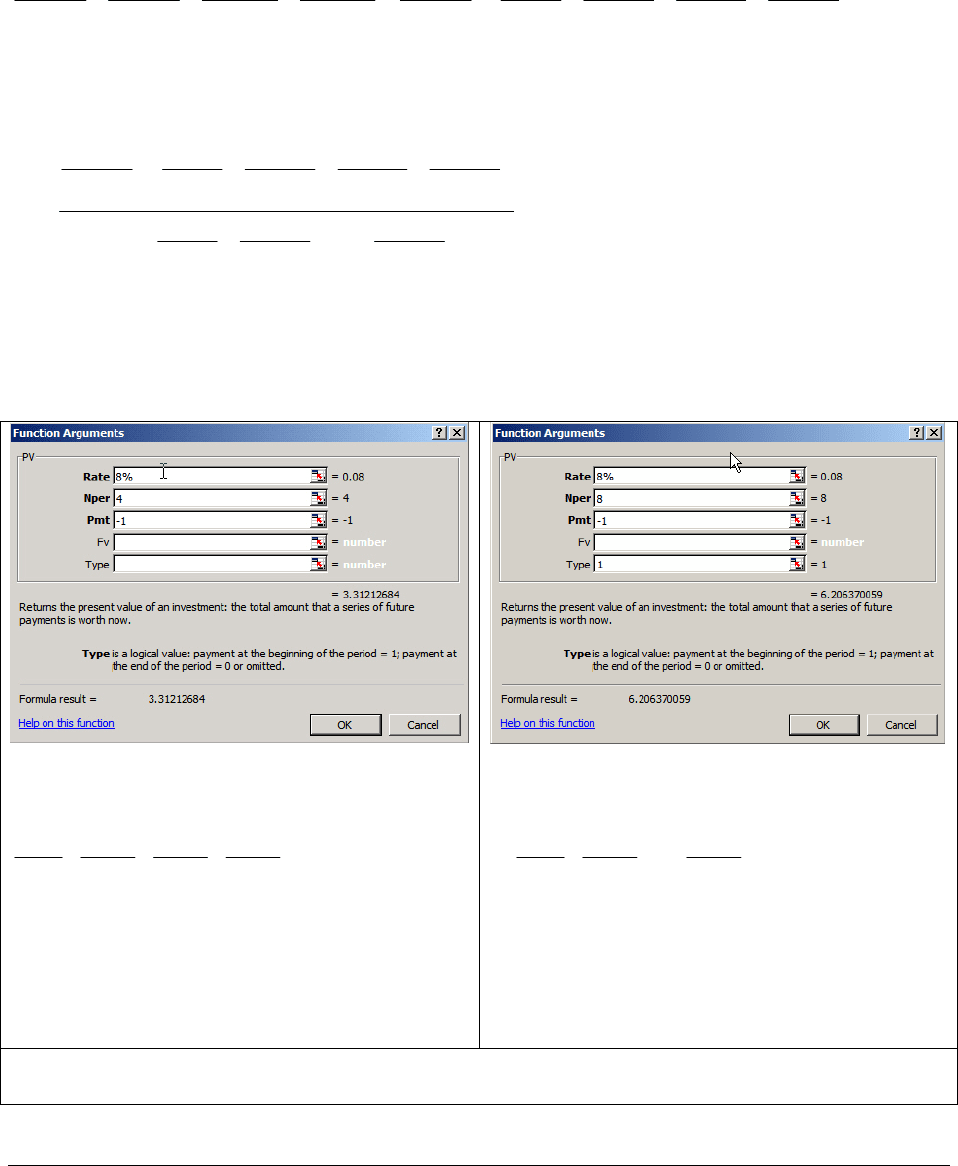
In Excel both the numerator and the denominator are computed by filling in the dialog box for

the

PV function:

The numerator:

()

()()()

234

1111

3.1212684

1.08

1.08 1.08 1.08

+++=

to complete the numerator, we have to multiply

()

20,000/ 1.08

The denominator:

()

() ()

11 1

1 6.206370059

1.08

1.08 1.08

++ ++ =…

Note that

Type is 1 (payments at beginning of

period).

Note that for both of these dialog boxes we’ve put in a negative payment Pmt. For the reason,

refer to our discussion on page000.

PFE Chapter 1, Time value of money page 47

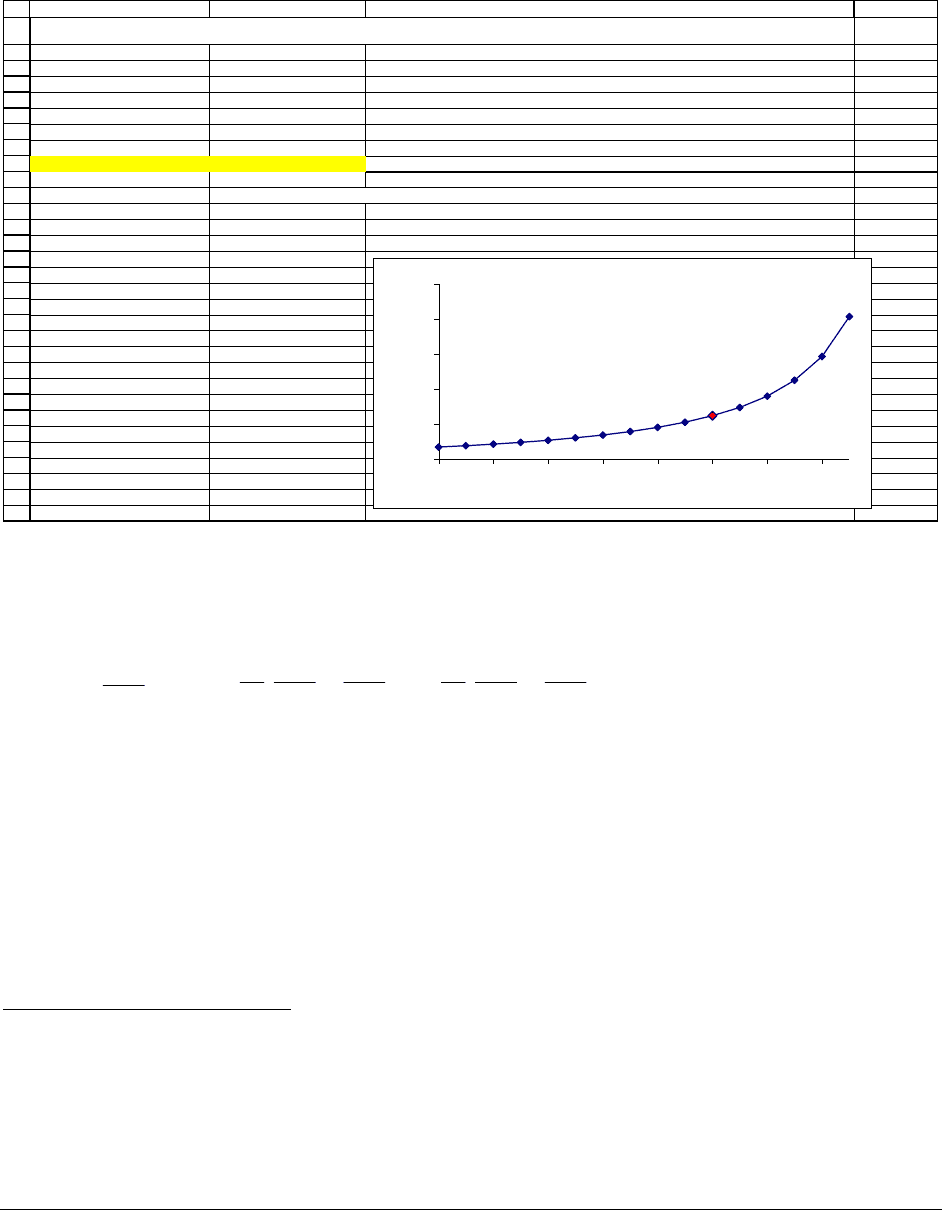
Rows 2-9 of the following spreadsheet show how we use these two PV functions to solve

for the annual deposit required:

AB C D

Linda's age when plan started 10

Linda's age at last deposit 17

Number of deposits 8 <-- =B3-B2+1

Number of withdrawals 4

Annual cost of college 20,000

Interest rate 8%

Annual deposit 6,227.78 <-- =(B6/(1+B7)^(B4-1))*PV(B7,4,-1)/PV(B7,B4,-1,,1)

Linda's age today Annual amount deposited

0 1,768.81 <-- =($B$6/(1+$B$7)^($B$3-A12))*PV($B$7,4,-1)/PV($B$7,$B$3-A12+1,-1,,1)

1 1,962.73 <-- =($B$6/(1+$B$7)^($B$3-A13))*PV($B$7,4,-1)/PV($B$7,$B$3-A13+1,-1,,1)

2 2,184.47 <-- =($B$6/(1+$B$7)^($B$3-A14))*PV($B$7,4,-1)/PV($B$7,$B$3-A14+1,-1,,1)

3 2,439.68

4 2,735.61

5 3,081.72

6 3,490.65

7 3,979.61

8 4,572.69

9 5,304.68

10 6,227.78

11 7,423.96

12 9,029.88

13 11,291.47

14 14,700.60

15 20,404.92

SAVING FOR COLLEGE--USING EXCEL FORMULAS ONLY

Annual Deposit Required to Fund 4 years of $20,000

when Linda is 17

5,000

10,000

15,000

20,000

25,000

02468101214

Linda's age at start of plan

The formula in cell B9 is the solution:

()

() () () ()

24 27

11 1 11 1

20,000

... 1 ...

1.08 1.08

1.08 1.08 1.08 1.08

1.08

=(B6/(1+B7)^ B4-1 )* PV(B7,B5,-1) / PV(B7,B4,-1,,1)

↑↑

↑

+++ ++++

  



The problem as initially set out assumed that Linda was 10 years old today. The table in rows 12

– 27 shows the problem solution for other starting ages.

The table in rows 12-27 would be simpler to compute if we used Data Table. This advanced feature of Excel is

explained in Chapter 30. The file Chapter01.xls on the disk accompanying Principles of Finance with Excel shows

how to use Data Table to do the calculations in rows 12-27.

PFE Chapter 1, Time value of money page 48

Pension plans

The savings problem of Linda’s parents is exactly the same as that faced by an individual

who wishes to save for his retirement. Suppose that Joe is 20 today and wishes to start saving so

that when he’s 65 he can have 20 years of $100,000 annual withdrawals. Adapting the previous

spreadsheet, we get:

AB C

Joe's age today 20

Joe's age at last deposit 64

Number of deposits 45 <-- =B3-B2+1

Number of withdrawals 20

Annual withdrawal from age 65 100,000

Interest rate 8%

Annual deposit 2,540.23 <-- =(B6/(1+B7)^(B4-1))*PV(B7,B5,-1)/PV(B7,B4,-1,,1)

Joe's age today Annual amount deposited

20 2,540.23 <-- =($B$6/(1+$B$7)^($B$3-A12))*PV($B$7,$B$5,-1)/PV($B$7,$B$3-A12+1,-1,,1)

22 2,978.96 <-- =($B$6/(1+$B$7)^($B$3-A13))*PV($B$7,$B$5,-1)/PV($B$7,$B$3-A13+1,-1,,1)

24 3,496.73 <-- =($B$6/(1+$B$7)^($B$3-A14))*PV($B$7,$B$5,-1)/PV($B$7,$B$3-A14+1,-1,,1)

26 4,109.02

28 4,834.85

30 5,697.73

32 6,727.03

34 7,959.85

35 8,666.90

38 11,239.91

40 13,430.03

42 16,123.53

44 19,471.60

46 23,688.86

48 29,090.61

50 36,159.79

SAVING FOR RETIREMENT

Annual Deposit Required to Fund 20 years of $100,000

when Joe is 65

5,000

10,000

15,000

20,000

25,000

30,000

35,000

40,000

20 25 30 35 40 45 50

Joe's age at start of plan

In the table in rows 12 – 27 you see the power of compound interest: If Joe starts saving

at age 20 for his retirement, an annual deposit of $2,540.23 will grow to provide him with his

retirement needs of $100,000 per year for 20 years at age 65. On the other hand, if he starts

saving at age 35, it will require $8,666.90 per year.

PFE Chapter 1, Time value of money page 49

1.9. Computing annual “flat” payments on a loan—Excel’s PMT function

You’ve just graduated from college and the balance on your student loan is $100,000.

You now have to pay the loan off over 10 years at an annual interest rate of 10%. The payment

is in “even payments”—meaning that you pay the same amount each year (although—as you’ll

soon see—the breakdown of each payment between interest and principal is different). How

much will you have to pay off?

Suppose we denote the annual payment by X. The correct X has the property that the

present value of all the payments equals the loan principal:

()() ()

23 10

100,000 ...

1.10

1.10 1.10 1.10

XX X X

=+ + ++

Rewriting the right-hand side slightly, you can see that

()() ()

23 10

This expression can

be calculated using

Excel's PV function

100,000

11 1 1

...

1.10

1.10 1.10 1.10

↑

++++



Here’s all this in an Excel spreadsheet: