Principles of Finance with Excel (Основы финансов c Excel)

Подождите немного. Документ загружается.

PFE Chapter 1, Time value of money page 30

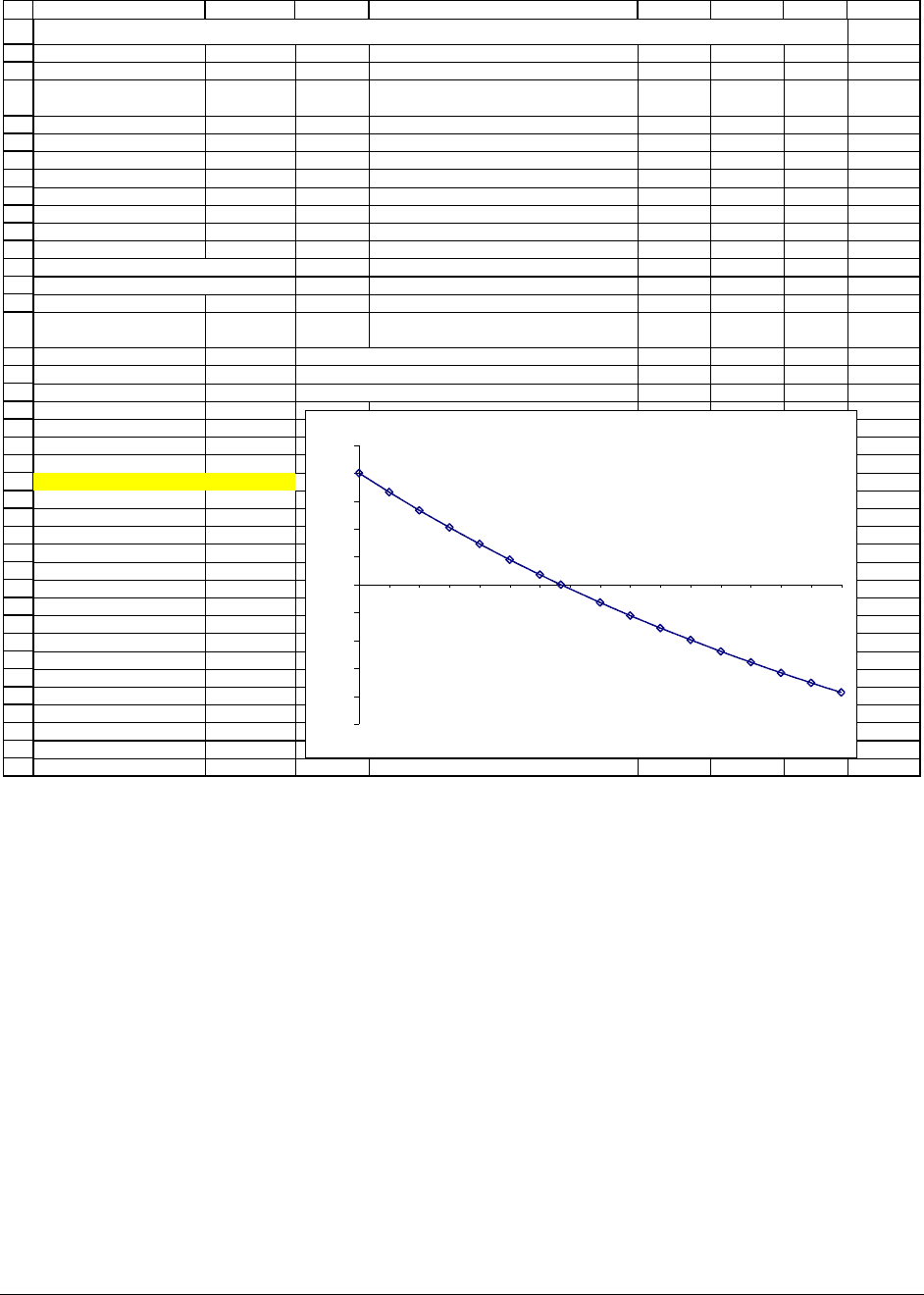
ABC D EFGH

r, interest rate 5%

Year

Payment

Present

value

-800

-800.00

1 100 95.24 <-- =B6/(1+$B$2)^A6

2 150 136.05 <-- =B7/(1+$B$2)^A7

3 200 172.77

4 250 205.68

5 300 235.06

NPV

Summing the present values 44.79 <-- =SUM(C5:C10)

Using Excel's NPV function 44.79 <-- =NPV($B$2,B6:B10)+C5

Discount

rate

NPV

0% 200.00 <-- =NPV(A17,$B$6:$B$10)+$B$5

1% 165.86 <-- =NPV(A18,$B$6:$B$10)+$B$5

2% 133.36 <-- =NPV(A19,$B$6:$B$10)+$B$5

3% 102.41

4% 72.92

5% 44.79

6% 17.96

6.6965% 0.00

8% -32.11

9% -55.48

10% -77.83

11% -99.21

12% -119.67

13% -139.26

14% -158.04

15% -176.03

16% -193.28

CALCULATING NET PRESENT VALUE (NPV) WITH EXCEL

NPV and the Discount Rate

-250

-200

-150

-100

-50

100

150

200

250

0% 1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 11% 12% 13% 14% 15% 16%

Discount rate

NPV

Note that we’ve indicated a special discount rate: When the discount rate is 6.6965%, the

net present value of the investment is zero. This rate is referred to as the internal rate of return

(IRR), and we’ll return to it in Section 000. For discount rates less than the IRR, the net present

value is positive, and for discount rates greater than the IRR the net present value is negative.

Using NPV to choose between investments

In the examples discussed thus far, we’ve used NPV only to choose whether to undertake

a particular investment or not. But NPV can also be used to choose between investments. Look

at the following spreadsheet: You have $800 to invest, and you’ve been offered the choice

PFE Chapter 1, Time value of money page 31

between Investment A and Investment B. The spreadsheet below shows that at an interest rate of

15%, you should choose Investment B because it has a higher net present value. Investment A

will increase your wealth by $219.06, whereas Investment B increases your wealth by $373.75.

ABC D

USING NPV TO CHOOSE BETWEEN INVESTMENTS

Discount rate 15%

Year

Investment

Investment B

-800

1 250 600

2 500 200

3 200 100

4 250 500

5 300 300

NPV 219.06 373.75 <-- =NPV(B2,C6:C10)+C5

To summarize:

In using the NPV to choose between two positive-NPV investments, we choose the

investment with the higher NPV.

There’s a possible exception to this rule: If we neither have the cash nor can borrow the money to make the

investment (the jargon is cash constrained), we may want to use the profitability index to choose between

investments. The profitability index is defined as the ratio of the PV(future cash flows) to the investment’s cost.

See Chapter 3 for a discussion of this topic.

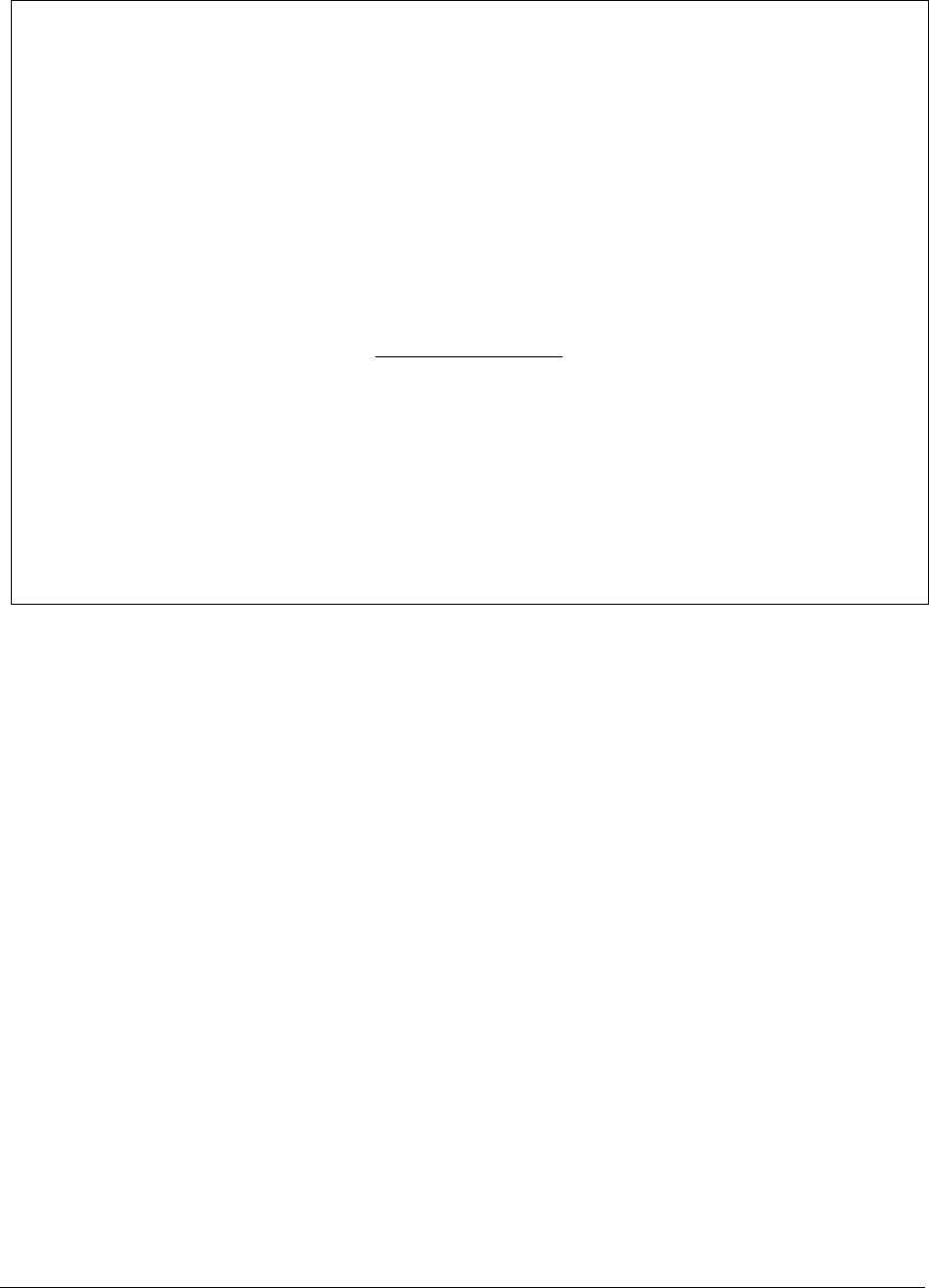
PFE Chapter 1, Time value of money page 32

1.4. The internal rate of return (IRR)

In this section we discuss the internal rate of return (IRR):

The IRR of a series of cash flows is the discount rate that sets the net present value of the

cash flows equal to zero.

Before we explain in depth (in the next section) why you want to know the IRR, we

explain how to compute it. Let’s go back to the example on page000: If you pay $800 today to

your local pawnshop, the owner promises to pay you $100 at the end of year 1, $150 at the end

of year 2, $200 at the end of year 3, $250 at the end of year 4 , and $300 at the end of year 5.

Discounting these cash flows at rate r, the NPV can be written:

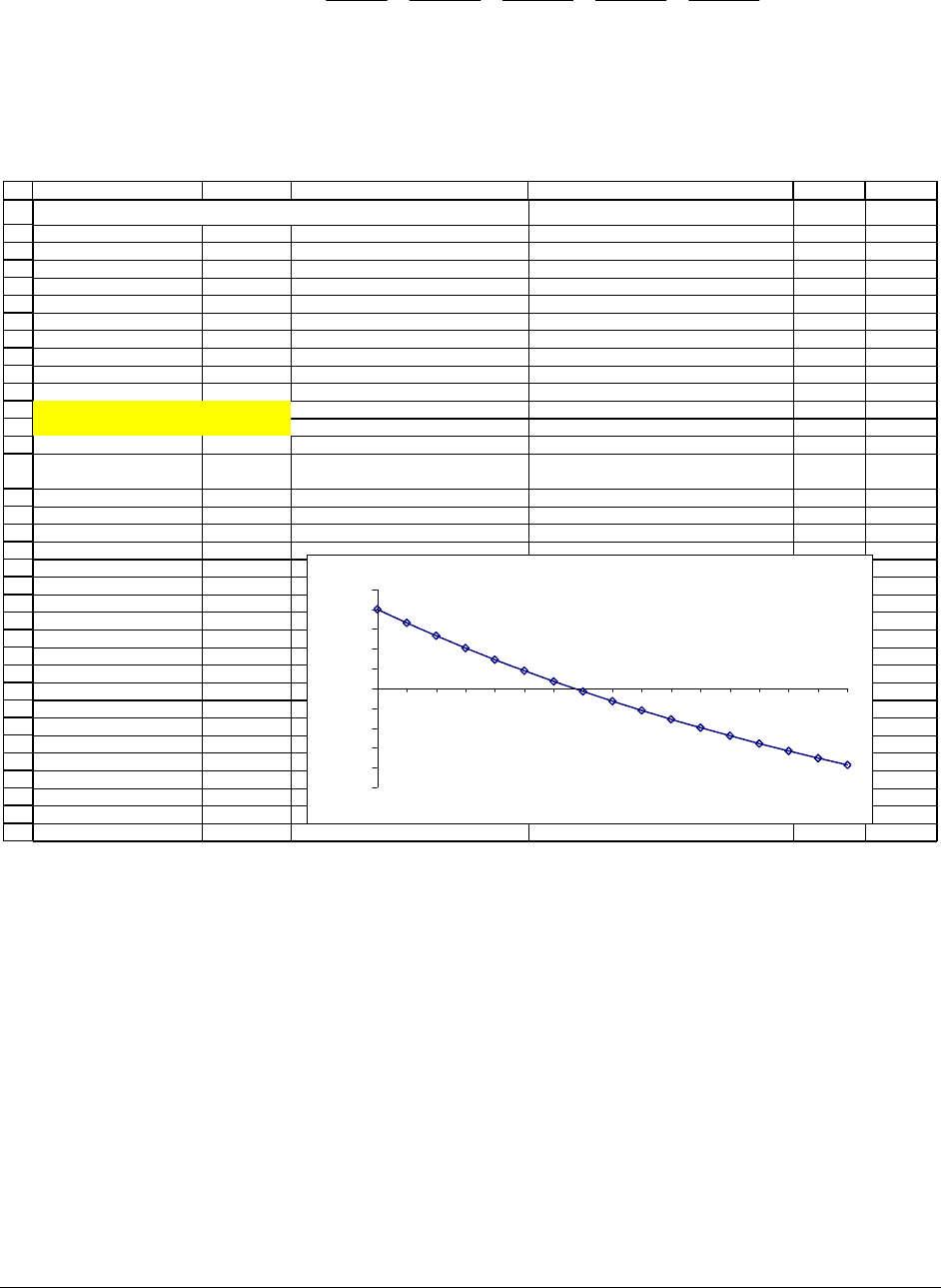
Nomenclature—Is it a discount rate or an interest rate?

In some of the examples above we’ve used discount rate instead of interest rate to

describe the rate used in the net present value calculation. As you will see in further chapters

of this book, the rate used in the NPV has several synonyms: Discount rate, interest rate, cost

of capital, opportunity cost—these are but a few of the names for the rate that appears in the

denominator of the NPV:

()

Cash flowin year t

Discount rate

Interest rate

Costof capital

Opportunity cost

↑

PFE Chapter 1, Time value of money page 33

()

()()()()

2345

100 150 200 250 300

800

1111

NPV

rrrr

=− + + + + +

++++

In cells B16:B32 of the spreadsheet below, we calculate the NPV for various discount rates. As

you can see, somewhere between

r = 6% and r = 7%, the NPV becomes negative.

AB C D EF

r, interest rate 6.6965%

Payment

-800

1100

2150

3200

4250

5300

NPV 0.00 <-- =NPV(B2,B6:B10)+B5

IRR 6.6965% <-- =IRR(B5:B10)

Discount

rate

NPV

0% 200.00 <-- =NPV(A16,$B$6:$B$10)+$B$5

1% 165.86 <-- =NPV(A17,$B$6:$B$10)+$B$5

2% 133.36 <-- =NPV(A18,$B$6:$B$10)+$B$5

3% 102.41

4% 72.92

5% 44.79

6% 17.96

7% -7.65

8% -32.11

9% -55.48

10% -77.83

11% -99.21

12% -119.67

13% -139.26

14% -158.04

15% -176.03

16% -193.28

CALCULATING THE IRR WITH EXCEL

NPV and the Discount Rate

-250

-200

-150

-100

-50

100

150

200

250

0% 1% 2% 3% 4% 5% 6% 7% 8% 9% 10% 11% 12% 13% 14% 15% 16%

Discount rate

NPV

In cell B13, we use Excel’s

IRR function to calculate the exact discount rate at which the

NPV becomes 0. The answer is 6.6965%; at this interest rate, the NPV of the cash flows equals

zero (look at cell B12). Using the dialog box for the Excel

IRR function:

PFE Chapter 1, Time value of money page 34

Dialog box for IRR function

Notice that we haven’t used the second option (“Guess”) to calculate our IRR. We discuss this

option in Chapter 4.

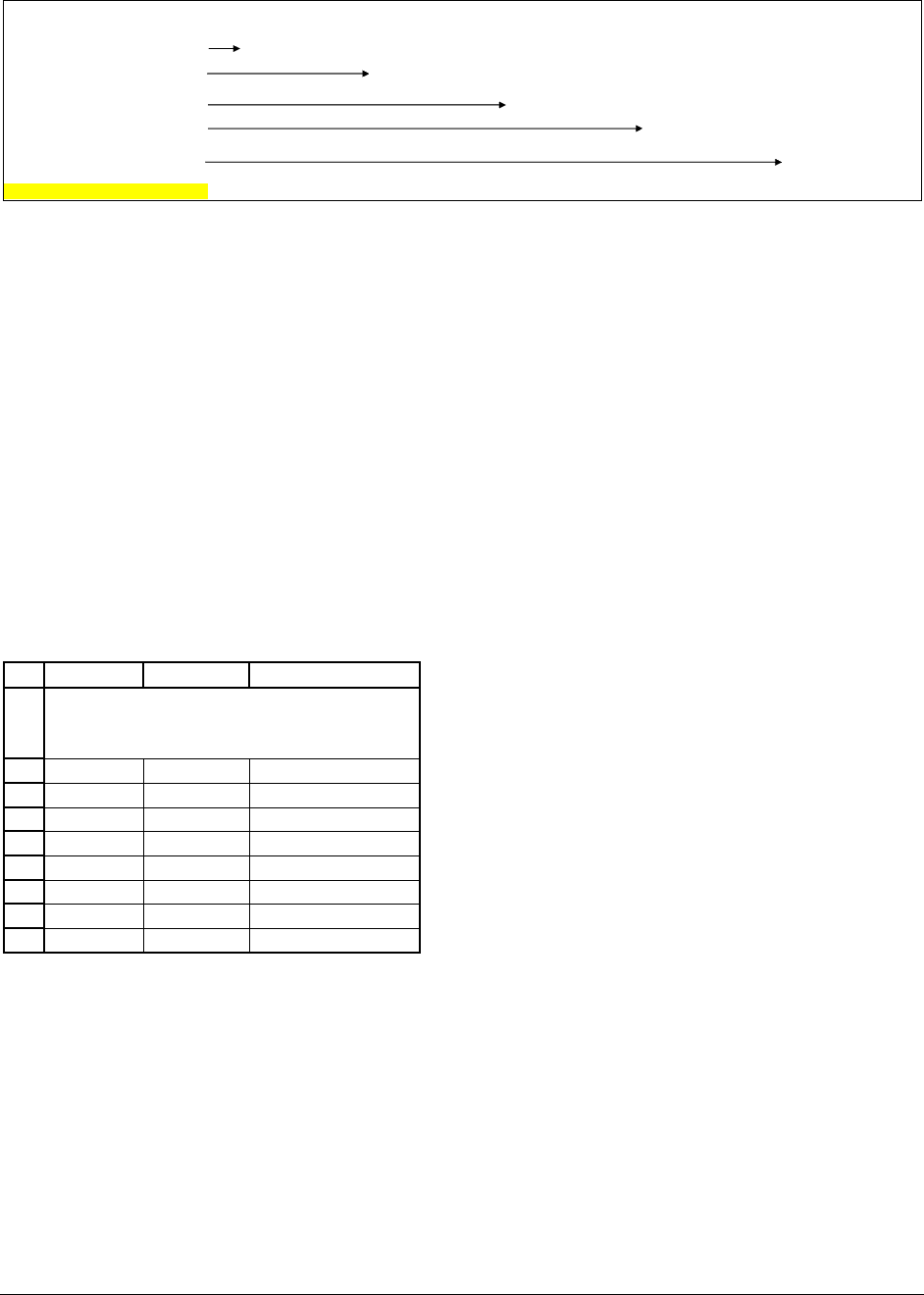
What does the IRR mean?

Suppose you could get 6.6965% interest at the bank and suppose you wanted to save

today to provide yourself with the future cash flows of the example on page000:

•

To get $100 at the end of year 1, you would have to put the present value

100

93.72

1.06965

= in the bank today.

•

To get $150 at the end of year 2, you would have to put its present value

()

150

131.76

1.06965

= in the bank today.

•

And so on … (see the picture below)

The total amount you would have to save is $800, exactly the cost of this investment

opportunity. This is what we mean when we say that:

The internal rate of return is the compound interest rate you earn on an investment.

PFE Chapter 1, Time value of money page 35

Time 0 1 2 3 4 5

Save for time 1's $100

$100/(1+6.6965%)

93.72

FV=93.72*(1+6.6965%)

=$100.00

Save for time 1's $150

$150/(1+6.6965%)

131.76

FV=131.76*(1+6.6965%)

= $150.00

Save for time 3's $200

$200/(1+6.6965%)

164.66

FV=164.66*(1+6.6965%)

= $200.00

Save for time 4's $250

$250/(1+6.6965%)

192.90

FV=192.90*(1+6.6965%)

=$250.00

Save for time 5's $300

$300/(1+6.6965%)

216.95

FV=216.95*(1+6.6965%)

= $300.00

Total saving at time 0

800.00

Using IRR to make investment decisions

The IRR is often used to make investment decisions. Suppose your Aunt Sara has been

offered the following investment by her broker: For a payment of $1,000, a reputable finance

company will pay her $300 at the end of each of the next four years. Aunt Sara is currently

getting 5% on her bank savings account. Should she withdraw her money from the bank to make

the investment? To answer the question, we compute the IRR of the investment and compare it

to the bank interest rate:

AB C

Year Cash flow

0 -1,000

1 300

2 300

3 300

4 300

IRR 7.71% <-- =IRR(B3:B7)

USING IRR TO MAKE

INVESTMENT DECISIONS

The IRR of the investment, 7.71%, is greater than 5% Sara can earn on her alternative

investment (the bank account). Thus she should make the investment.

Summarizing:

PFE Chapter 1, Time value of money page 36

In using the IRR to make investment decisions, an investment with an IRR greater than

the alternative rate of return is a good investment and an investment with an IRR less

than the alternative rate of return is a bad investment.

Using IRR to choose between two investments

We can also use the internal rate of return to choose between two investments. Suppose

you’ve been offered two investments. Both Investment A and Investment B cost $1,000, but

they have different cash flows. If you’re using the IRR to make the investment decision, then

you would choose the investment with the

higher IRR. Here’s an example:

AB C D

Year

Investment A

cash flows

Investment B

cash flows

0 -1,000.00 -1,000.00

1 450.00 550.00

2 425.00 300.00

3 350.00 475.00

4 450.00 200.00

IRR 24.74% 22.26% <-- =IRR(C3:C7)

USING IRR TO CHOOSE BETWEEN

INVESTMENTS

We would choose Investment A, which has the higher IRR.

To summarize:

In using the IRR to choose between two comparable investments, we choose the

investment which has the higher IRR.

[This assumes that: 1) Both investments have IRR

greater than the alternative rate. 2) The investments are of comparable risk.]

PFE Chapter 1, Time value of money page 37

Using NPV and IRR to make investment decisions

In this chapter we have now developed two tools, NPV and IRR, for making investment

decisions. We’ve also discussed two kinds of investment decisions. Here’s a summary:

“Yes or No”:

Choosing whether to

undertake a single investment

“Investment ranking”:

Comparing two investments

which are mutually exclusive

NPV criterion

The investment should be

undertaken if its NPV > 0:

Investment A is preferred to

investment

B if

NPV(A) > NPV(B)

IRR criterion

The investment should be

undertaken if its IRR >

where

r is the appropriate

discount rate.

Investment

A is preferred to

investment

B if

IRR(A) > IRR(B).

In Chapter 3 we discuss further implementation of these two rules and two decision

problems.

1.5. What does IRR mean? Loan tables and investment amortization

In the previous section we gave a simple illustration of what we meant when we said that

the internal rate of return (IRR) is the compound interest rate that you earn on an asset. This

simple sentence—which is not easy to understand—underlies a slew of finance applications:

When finance professionals discuss the “rate of return” on an investment or the “effective

interest rate” on a loan, they are almost always refering to the IRR. In this section we explore

some meanings of the IRR. Almost the whole of Chapter 2 is devoted to this topic.

PFE Chapter 1, Time value of money page 38

A simple example

Suppose you buy an asset for $200 today and that the asset has a promised payment of

$300 in one year. The IRR is 50%; to see this recall that the IRR is the interest rate which makes

the NPV zero. Since the investment NPV

300

200

1 r

=− +

, this means that the NPV is zero when

300

11.5

200

r+= =

. Solving this simple equation gives r = 50%.

Here’s another way to think about this investment and its 50% IRR:

•

At time zero you pay $200 for the investment.

•

At time one, the $300 investment cash flow repays the initial $200. The remaining $100

represents a 50% return on the initial $200 investment. This is the IRR.

The IRR is the rate of return on an investment; it is the rate that repays, over the life of

the asset, the initial investment in the asset and that pays interest on the outstanding

investment balances.

A more complicated example

We now give a more complicated example, which illustrates the same point. This time,

you buy an asset costing $200. The asset’s cash flow are $130.91 at the end of year 1 and

$130.91 at the end of year 2. Here’s our IRR analysis of this investment:

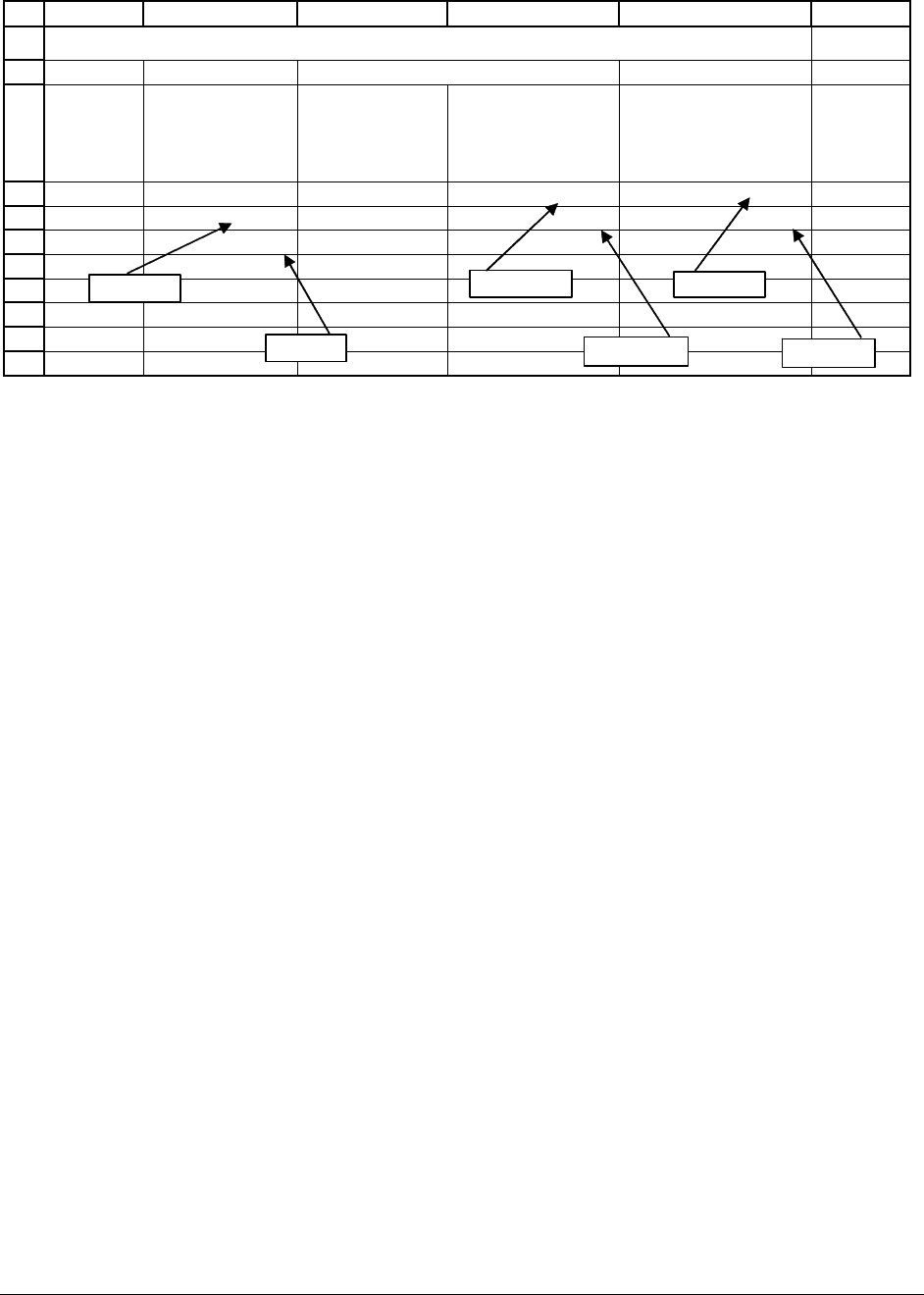
PFE Chapter 1, Time value of money page 39

AB C D E F

IRR 20.00% <-- =IRR({-200,130.91,130.91})

Year

Investment

at beginning

of year

Payment at

end of year

Part of payment

which is interest

Part of payment

which is repayment

of principal

1 200.00 130.91 40.00 90.91

2 109.09 130.91 21.82 109.09

30.00

THE IRR AS A RATE OF RETURN ON AN INVESTMENT

=$B$2*B4

=C4-D4

=B4-E4

=$B$2*B5

=C5-D5

=B5-E5

•

The IRR for the investment is 20.00%. Note how we calculated this—we simply typed

into cell B2 the formula

=IRR({-200,130.91,130.91}) (if you’re going to use this method

of calculating the IRR in Excel, you have to put the cash flows in the curly brackets).

•

Using the 20% IRR, $40.00 (=20%*$200) of the first year’s payment is interest, and the

remainder—$90.91—is repayment of principal. Another way to think of the $40.00 is to

consider that to buy the asset, you gave the seller the $200 cost of the asset. When he

pays you $130.91 at the end of the year, $40 (=20%*$200) is interest—your payment for

allowing someone else to use your money. The remainder, $90.91, is a partial repayment

of the money lent out.

•

This leaves the outstanding principal at the beginning of year 2 as $109.09. Of the

$130.91 paid out by the investment at the end of year 2, $21.82 (=20%*109.09) is

interest, and the rest (exactly $109.09) is repayment of principal.

•

The outstanding principal at the beginning of year 3 (the year after the investment

finishes paying out) is zero.