Povh B., Rith K., Scholz Ch., Zetsche F. Particles and Nuclei: An Introduction to the Physical Concepts

Подождите немного. Документ загружается.

302 18 Collective Nuclear Excitations

232

a) b)

24/h

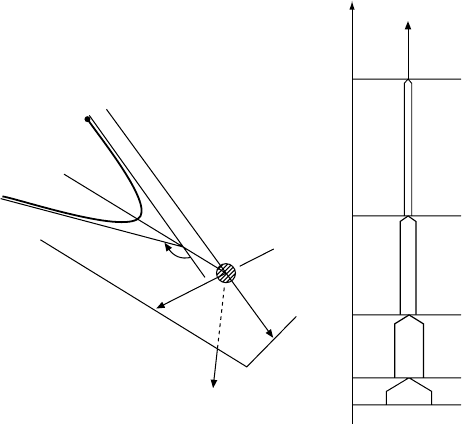
Fig. 18.9. (a) Kinematics of a heavy ion collision (here

Zr+

232

Th). The projectile

follows a hyperbolic orbit in the Coulomb ﬁeld of the target nucleus. (b)Sketchof

multiple Coulomb excitation of a rotation band. Successive quadrupole excitations

lead to the 2

,... states being populated (with decreasing intensity).

just below where the ﬁrst non-electromagnetic eﬀects would make themselves

felt.

The

Zr projectile nucleus follows a hyperbolic path in the ﬁeld of the

target nucleus (Fig. 18.9a) and exposes the

232

Th nucleus to a rapidly chang-

ing electric ﬁeld. The path of the ion is so sharply curved that frequencies

in the time dependent electric ﬁeld are generated that are high enough to

produce individual excitations with energies up to about 1 MeV.

There is not just a quantitative but also a qualitative diﬀerence between

Coulomb excitation and electron scattering oﬀ nuclei:

– The principal distinction is that the interaction is much stronger with a

projectile charge which is Z times that of the electron. One must replace

α by Zα in the matrix element (5.31). This means that the cross-section

increases as Z

– If we are not to cross the Coulomb threshold, the projectile energy must

be so low that its velocity obeys v

∼

0.05 c. Magnetic forces are hence of

little importance.

– The ion orbit may be calculated classically, even for inelastic collisions. The

kinetic energy of the projectile in Coulomb excitation changes by less than

1 % and thus its path is practically the same. The frequency distribution of

18.4 Rotation States 303

Counts/0.5keV

80 160 240 320 400 480

EJ [keV]

9 11 13 15

6 8

–

(J–2)

–

(J–2)

791113

–

(J+1)

x-rays

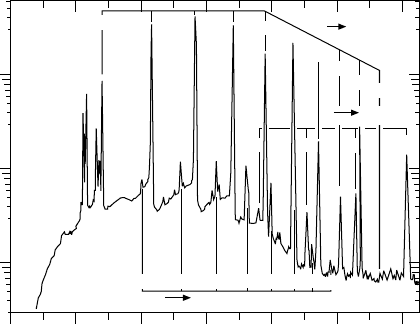
Fig. 18.10. Photon spectrum of a Coulomb excited

232

Th nucleus. Three series

of matching lines may be seen. The strongest lines correspond to transitions in

the ground state rotation band J

→ (J − 2)

. The other two bands are strongly

suppressed and are the results of excited states (cf. Fig. 18.12) [Ko88].

the virtual photons is very well known and the transition amplitudes can

be worked out to a high degree of accuracy.

The large coupling strength means that successive excitation from one

level to the next is now possible. This is sketched in Fig. 18.9b: the quadrupole

excitation reproduces itself inside a rotation band from the 2

state via the

to the 6

The popularity of Coulomb excitation in gamma spectroscopy is well

founded. In such reactions we primarily produce states inside rotation bands.

The cross-sections into the excited states give us, through the transition prob-

abilities, the most important information about the collective nature of the

rotation bands. Measurements of the cross-sections into the various states si-

multaneously determine the transition probability for the electric quadrupole

transition inside the rotation band.

The introduction of germanium semiconductor detectors has marked a

very signiﬁcant step forward in nuclear-gamma spectroscopy. The low energy

part of the gamma spectrum of Coulomb excitation of

232

Th from scattering

with

Zr ions is shown in Fig. 18.10. This gamma spectrum was recorded

with a Ge-semiconductor counter and a coincidence condition for the back-

wardly scattered

Zr ions, which were measured with a Si-semiconductor

detector (Fig. 18.11).

Excellent energy resolution makes it possible to see individual transitions

inside rotation bands. Three series of lines can be recognised. The strongest

are transitions inside the ground state rotation band (J

→ (J − 2)

). Ac-

304 18 Collective Nuclear Excitations

NaI-Crystals

415 MeV

Zr -Beam

232

Th -Target

Si -Detector

Ge - Detector

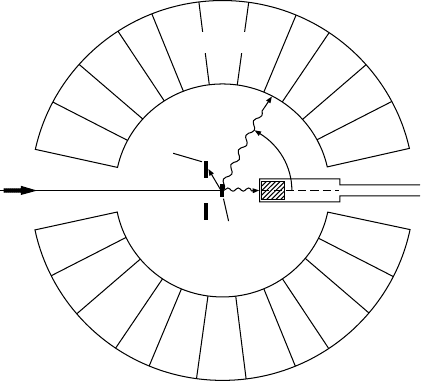
Fig. 18.11. Experimental apparatus for investigating Coulomb excitation in heavy

ion collisions. In the example shown a

Zr beam hits a

232

Th target. The back-

wardly scattered Zr projectiles are detected in a silicon detector. A germanium de-

tector, with which the γ cascades inside the rotation bands can be ﬁnely resolved,

gives a precise measurement of the γ spectrum. These photons are additionally

measured by a crystal ball of NaI crystals with a poorer resolution. A coincidence

condition between the silicon detector and the NaI crystals can be used to single

out an energy window inside which one may study the nuclear rotation states with

the germanium detector (from [Ko88]).

cording to (18.42) these lines should be equidistantly spaced out. This is only

approximately the case. This may be explained by noting that the moment

of inertia increases with the spin. Events with scattering angles around 180

◦

are chosen because the projectile must then have got very close to the tar-

get and then at the moment of closest approach have experienced a strong

acceleration. The virtual photon spectrum which the projectile emits con-

tains high frequencies which are important for the excitation of the high spin

states. The spectrum which emerges from this sort of measurement is shown

in Fig. 18.12: as well as the ground state rotation band, there are other ro-

tation bands which are built upon excited states. In this case the excitations

may be understood as vibratory states.

Fusion reactions. Records in high spin excitations may be obtained with

the help of fusion reactions such as

Ca +

108

Pd −→

156

Dy −→

152

Dy + 4n .

Ca nuclei with a kinetic energy of 200 MeV can just break through the

Coulomb barrier. If the fusion process takes place when the nuclei just touch,

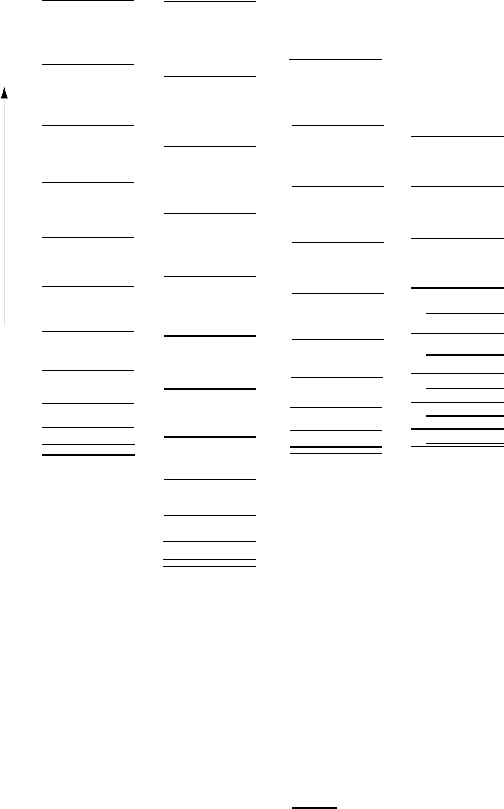
18.4 Rotation States 305

3248

2831

2440.3

2080.3

3619

3144

2691.4



3617.3



3204.7



2813.9



2445.7



2102.0

2262.4

1858.7

1754.7

2766.1

2445.3

2117.1

1801.4

1482.5

1467.5



1784.9



1498.8



1249.6

1051.2

1513.0

1260.7

890.5

785.5



1043.1



883.8



714.3

1137.1

826.8

556.9

333.2

162.0

49.4

1222.3

1023.4

873.1

774.5



774.5

730.6

~1641

~1371

~1142

829.7

960.3



232

[keV]

Fig. 18.12. Spectrum of the

232

Th nucleus. The excitation energies are in keV. As

well as the ground state rotation band, which may be excited up to J

=24

,other

rotation bands have been observed which are built upon vibrational excitations

(from [Ko88]). The quantum numbers of the vibrational states are given below the

bands. For reasons of symmetry, the only rotation states which can be constructed

upon the J

−

vibrational state are those with odd angular momenta.

then the

156

Dy fusion product receives angular momentum

 ≈ (R

+ R

)

√

2mE , (18.47)

where m is the reduced mass of the

Ca–

108

Pd system. R

and R

are

of course the correct nuclear radii from (5.56). The calculation thus yields

 ≈ 180. In practice the fusion reaction only takes place if the projectile and

target overlap, so this number should be understood as an upper limit on the

accessible angular momentum. Experimentally states up to J

=60

have

been reached in this reaction (Fig. 18.14).

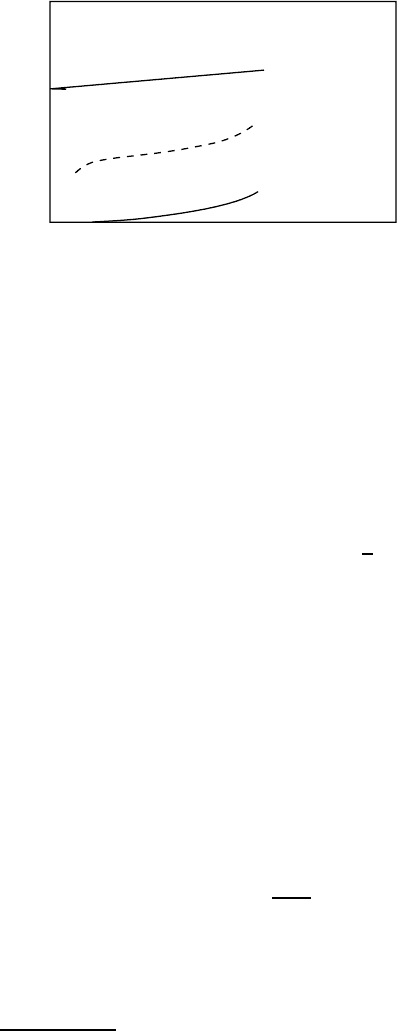
306 18 Collective Nuclear Excitations

rigid

ellipsoid

experiment

irrotational

flow

deformation G

T/T

rigid shpere

Fig. 18.13. Moments of in-

ertia of deformed nuclei com-

pared with a rigid sphere as

a function of the deforma-

tion parameter δ.Theex-

treme cases of a rigid ellip-

soid and an irrotational liq-

uid are given for comparison.

The moment of inertia. The size of the moment of inertia can with the

aid of (18.44) be extracted from the measured energy levels of the rotation

bands. The deformation δ can be obtained from the electric quadrupole ra-

diation transition probability inside the rotation band. The matrix element

for the quadrupole radiation is proportional to the quadrupole moment of

the nucleus, which, for collective states, is given by (17.40). The observed

connection between the moment of inertia and the deformation parameter is

displayed in Fig. 18.13. Note that the nuclear moments of inertia are nor-

malised to those of a rigid sphere with radius R

rigid sphere

. (18.48)

The moment of inertia increases with the deformation and is about half that

of a rigid sphere.

Two extremal models are also shown in Fig. 18.13. The moment of inertia

is maximised if the deformed nucleus behaves like a rigid body. The other

limit is reached if the nucleus behaves like an irrotational liquid.

Superﬂuid

He is an example of an ideal ﬂuid, incompressible and fric-

tionless. Currents in an frictionless liquid are irrotational. A massless eggshell

ﬁlled with superﬂuid helium would as it rotated have the moment of inertia of

an irrotational current. Only the swelling out of the egg, and not the interior,

would contribute to the moment of inertia. The moment of inertia for such

an object is

Θ =

45δ

16π

· Θ

rigid sphere

, (18.49)

where δ is the deformation parameter from (17.39).

Let us return to the example of the

232

Th nucleus. The transition prob-

abilities yield a deformation parameter of δ =0.25. If the rotation of the

The comparison with a rigid sphere is, of course, purely classical; a spherically

symmetric quantum mechanical system cannot rotate.

18.4 Rotation States 307

nucleus could be described as that of an irrotational current, then its mo-

ment of inertia would, from (18.49), have to be 6 % of that of a rigid sphere.

The level spacings of the ground state band yield, however

232

rigid sphere

≈ 0.3 . (18.50)

This implies that the experimentally determined moment of inertia lies be-

tween the two extremes (Fig. 18.13).

This result may be understood at a qualitative level rather easily. We

mentioned in Sect. 17.4 that nuclear deformation is a consequence of an

accumulation of mutually attractive orbitals either parallel to the symmetry

axis (prolate shape) or perpendicular to it (oblate shape). The deformation is

associated with the orbitals and one would expect deformed nuclei to rotate

like rigid ellipsoids; but this clearly does not happen. This deviation from the

rotation of a rigid rotator implies that nuclear matter must have a superﬂuid

component. Indeed nuclei behave like eggshells that are ﬁlled with a mixture

of a normal ﬂuid and a superﬂuid.

The superﬂuid components of nuclear matter are presumably generated

by the pairing force. Nucleons with opposite angular momenta combine to

form pairs with spin zero (cf. p. 263). Such zero spin systems are spheri-

cally symmetric and cannot contribute to the rotation. The pair formation

may be understood analogously to the binding of electrons in Cooper pairs

in superconductors [Co56b, Ba57]. The paired nucleons represent, at least

as far as rotation is concerned, the superﬂuid component of nuclear mat-

ter. This means on the other hand that not all nucleons can be paired oﬀ

in deformed nuclei; the larger the deformation, the more nucleons must re-

main unpaired. This explains why the moment of inertia increases with the

deformation (Fig. 18.13).

A similar dependence of the moment of inertia upon the unpaired nucleons

can be seen in the rotation bands. The speed of rotation of the nucleus,

and hence the centrifugal force upon the nucleons, increases with angular

momentum. This causes nucleon pairs to break apart. Thus for large angular

momenta the moment of inertia approaches that of a rigid rotator, as one

can vividly demonstrate in

152

Dy.

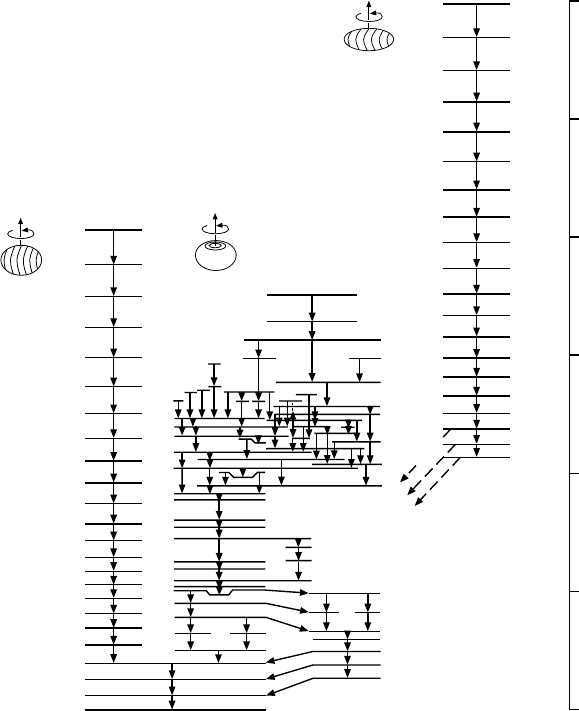
The excitation spectrum of

152

Dy (Fig. 18.14) is more than a little exotic.

The ground state of

152

Dy is not strongly deformed, as one sees from the

fact that the levels in the ground state rotation band do not strictly follow

the E ∝ J(J + 1) law and that transition probabilities are small. This band,

in which the 0

until 46

states have been observed, ﬁrst shows a genuine

rotational character for high spins. The band which goes up to J

=60

particularly interesting [Tw86]. The moment of inertia of this band is that of

a rigid ellipsoid whose axes have the ratios 2 : 1 :1 [Ra86]. The transition prob-

abilities inside this band are of the order of 2000 single particle probabilities.

Additionally to these two rotation bands, which have a prolate character,

308 18 Collective Nuclear Excitations

[MeV]

152

–

prolate

oblate

prolate

superdeformed

Fig. 18.14. Energy levels of

152

Dy [Sh90]. Although the low energy levels do not

display typical rotation bands, these are seen in the higher excitations, which implies

that the nucleus is then highly deformed.

states have been found which may be interpreted as those of an oblately de-

formed nucleus. Evidently

152

Dy has two energy minima near to its ground

state, a prolate and an oblate shape. This example shows very nicely that for

nuclei with incomplete shells a deformed shape is more stable than a sphere.

Tiny changes in the conﬁguration of the nucleus decide whether the prolate

or oblate form is energetically favoured (Fig. 17.10).

Problems 309

Further excitations of deformed nuclei. We have here only treated the

collective aspects of rotation. Generally, however, excitations occur where,

as well as rotation, an oscillation around either the equilibrium shape of the

deformed nucleus or single particle excitations are seen. (The latter case may

be particularly clearly seen in odd nuclei.) The single particle excitations may

be, as described in Sect. 17.4, calculated from the movement of nucleons in

a deformed potential. Deformed nuclei may be described, similarly to their

vibrating brethren, in a hybrid model which employs collective variables for

the rotating and vibrating degrees of freedom. The single particle motion

is coupled to these collective variables. The names of Bohr and Mottelson

in particular are associated with the work that showed that a consistent

description of nuclear excitations is possible in such hybrid models.

Problems

1. The electric dipole giant resonance

a) How large is the average deviation between the centres of mass of the pro-

tons and neutrons in giant dipole resonances for nuclei with Z = N = A/2?

The A dependence of the resonance energy is very well described by ω ≈

80 MeV/A

1/3

. Give the numerical value for

Ca.

b) Calculate the squared matrix element for the dipole transition in this model.

c) Calculate the matrix element for a proton or neutron dipole transition (18.36)

in the shell model with a harmonic oscillator potential. Use the fact that sin-

gle particle excitations are about half the size of those of the giant resonance.

2. Deformation

The deformation parameter of the

176

Lu nucleus is δ =+0.31. Find the semi-

axes a and b of the rotational ellipsoid, describe its shape and calculate the

quadrupole moment of this nucleus.

3. Rotational bands

The rotational band of

152

Dy in Fig. 18.14 which extends up to J

=60

corresponds to the rotation of an ellipsoid the ratio of whose axes is 2 : 1 : 1.

What would be the velocity of the nucleons at the “tip” of the ellipsoid if this

was a rotating rigid body? Compare this velocity with the average speed of

nucleons in a Fermi gas with p = p

= 250 MeV/c.

19 Nuclear Thermodynamics

Up to now we have concerned ourselves with the properties of nuclei in the

ground state or the lower lying excited states. We have seen that the ob-

served phenomena are characterised, on the one hand, by the properties of a

degenerate fermion system and, on the other, by the limited number of the

constituents. The nuclear force generates, to a good approximation, an overall

mean ﬁeld in which the nucleons move like free particles. In the shell model

the ﬁnite size of nuclei is taken into account and the states of the individual

nucleons are classiﬁed according to radial excitations and angular momenta.

Thermodynamically speaking, we assign such systems zero temperature.

In the ﬁrst part of this chapter we want to concern ourselves with highly

excited nuclei. At high excitation energies the mean free path of the nucleon

inside the nucleus is reduced; it is only about 1 fm. The nucleus is then no

longer a degenerate fermionic system, but rather resembles, ever more closely

for increasing excitations, the state of a normal liquid. It is natural to use

statistical methods in the description of such systems. A clear description

may be gained by employing thermodynamical quantities. The excitation of

the nucleus is characterised by the temperature. We should not forget that

strictly speaking one can only associate a temperature to large systems in

thermal equilibrium and even heavy nuclei do not quite correspond to such

a system. As well as this, excited nuclei are not in thermal equilibrium, but

rather rapidly cool down via the emission of nucleons and photons. In any

thermodynamical interpretation of experimental results we must take these

deﬁciencies into account. In connection with nuclear thermodynamics one

prefers to speak about nuclear matter rather than nuclei, which implies that

many experimental results from nuclear physics may be extrapolated to large

systems of nucleons. As an example of this we showed, when we considered

the nuclear binding energy, that by taking the surface and Coulomb energies

into account one can calculate the binding energy of a nucleon in nuclear

matter. This is just the volume term of the mass formula, (2.8).

Heavy ion reactions have proven themselves especially useful in the

investigation of the thermodynamical properties of nuclear matter. In

nucleus-nucleus collisions the nuclei melt together to form for a brief time

a nuclear matter system with increased density and temperature. We will try

below to describe the phase diagram of nuclear matter using experimental

and theoretical results about these reactions.

312 19 Nuclear Thermodynamics

The results of nuclear thermodynamics are also of great importance for

cosmology and astrophysics. According to our current understanding, the

universe in the early stages of its existence went through phases where its

temperature and density were many orders of magnitude higher than in the

universe of today. These conditions cannot be reconstructed in the laboratory.

Many events in the history of the universe have, however, left lasting traces.

With the help of this circumstantial evidence one can try to draw up a model

of the development of the universe.

19.1 Thermodynamical Description of Nuclei

We have already in Sect. 3.4 (Fig. 3.10) distinguished between three sorts of

excitations in nuclei:

– The ground state and the low-lying states can be described in terms of

single particle excitations or via collective motion. This was treated in

Chapters 17 and 18.

– Far above the particle threshold there are no discrete states but only a

continuum.

– In the transition region below and barely above the particle threshold there

are lots of narrow resonances. These states do not, however, contain any

information about the structure of the nucleus. The phenomena in this

energy range in nuclei are widely referred to as quantum chaos.

In the following we shall concern ourselves with the last two of these domains.

Their description involves statistical methods and so we will initially turn our

attention to the concept of nuclear temperature.

Temperature. We want to introduce the idea of temperature in nuclear

physics through the example of the spontaneous ﬁssion of

252

Cf. The half life

252

Cf is 2.6 years and it has a 3.1 % probability of decaying via spontaneous

ﬁssion. There is some friction in the separation of the ﬁssion fragments and

so not all of the available energy from the ﬁssion process is converted into

kinetic energy for the fragments. Rather the internal energy of the fragments

is increased: the two fragments heat up.

The cooling down process undergone by the ﬁssion fragments is shown

schematically in Fig. 19.1. Initially cooling down takes place via the emission

of slow neutrons. Typically 4 neutrons are emitted, each of them carrying oﬀ,

on average, 2.1 MeV. Once the fragments have cooled below the threshold

for neutron emission, they can only cool further by photon emission.

The energy spectrum of the emitted neutrons has the form of a evapora-

tion spectrum. It may be described by a Maxwell distribution:

) ∼



· e

−E

/kT

. (19.1)