Povh B., Rith K., Scholz Ch., Zetsche F. Particles and Nuclei: An Introduction to the Physical Concepts

Подождите немного. Документ загружается.

252 17 The Structure of Nuclei

300

200

100

+20 0 –20

[

MeV

]

Counts

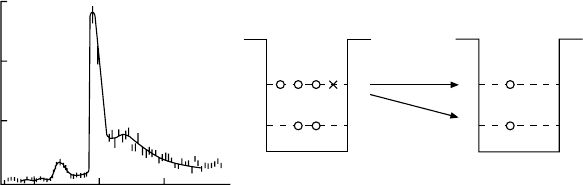
Fig. 17.3. The pion spectrum from the reaction K

−

C → π

−

Cfora

kaon momentum of 720 MeV/c [Po81]. The pion counting rate at 0

◦

is plotted as

a function of the transferred energy B

, which may be interpreted as the binding

energy of the Λ in the nucleus. Peak no. 1 corresponds to binding energy B

and peak no. 2, which is the

C ground state, has a binding energy of 11 MeV.

We have the following explanation for this. The Pauli principle prevents a

proton or a neutron in the nucleus from occupying a lower energy level that is

already “taken” – the states in the nucleus get ﬁlled “from the bottom up”. If

we, however, change a neutron into a Λ particle, then this can occupy any of

the states in the nucleus. The Λ does not experience the individual presence

of the nucleons, but rather just the potential that they create. This potential

is, it should be noted, shallower than that which the nucleons experience.

This is because the Λ-nucleon interaction is weaker than that between the

nucleons themselves. That this is the case may also be seen from the lack of

any bound state formed from a Λ and a single nucleon.

The spectrum of Fig. 17.3 now makes sense: the protons and neutrons in

the

C nucleus occupy 1s and 1p energy levels and should one of the neutrons

in a 1p state be transformed into a Λ, then this can also take up a 1p state.

In this case the binding energy of the Λ is close to zero. Alternatively it can

land in a 1s state and it then has a binding energy of about B

≈ 11 MeV.

The smeared out peak with B

< 0 can be interpreted as arising from

the transformation not of weakly bound neutrons near the Fermi level, but

rather of deeper lying neutrons.

The Λ one-particle states may be seen even more clearly in heavier nuclei.

Systematic investigations, based upon the reaction

+A→

A+K

, (17.21)

have yielded the binding energies of the 1s states and, furthermore, those of

the excited p, d and f states for various nuclei as shown in Fig. 17.4. This

shows the dependence of these binding energies upon the mass number A in

the nuclei concerned.

17.3 The Shell Model 253

0 0.05 0.10 0.15 0.20

-2/3

MeV

[

]

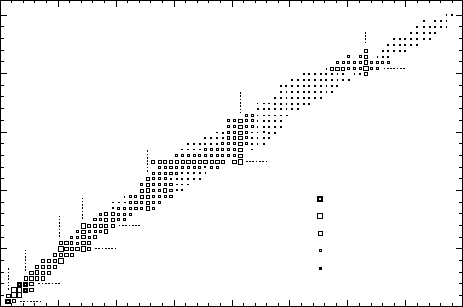
Fig. 17.4. The binding energy of Λ particles in hypernuclei as a function of the

mass number A [Ch89]. The symbols s

and d

refer to the state of the Λ in

the nucleus. The triangles which are connected by the dashed lines are theoretical

predictions.

In this way it is seen that the Λ hyperons occupy discrete energy levels,

whose binding energies increase with the mass number. The curves shown are

the results of calculations assuming both a potential with uniform depth V

≈

30 MeV and that the nuclear radius increases as R = R

1/3

[Po81, Ch89].

The scale A

−2/3

corresponds then to R

−2

and was chosen because B

almost constant for states with the same quantum numbers, cf. (16.13).

The agreement between the calculated binding energies of the Λ particles

and the experimental results is amazing, especially if one considers how simple

the potential well is. The Λ moves as a free particle in the well although the

nucleus is composed of densely packed matter.

17.3 The Shell Model

The consequences that we have drawn from the spectroscopy of the hyper-

nuclei can be directly applied to the nucleons and we may assume that each

nucleon occupies a well-deﬁned energy level.

The existence of these discrete energy levels for the nucleons in the nucleus

is reminiscent of the atomic electron cloud. The electrons move in the atom

in a central Coulombic potential emanating from the atomic nucleus. In the

nucleon, on the other hand, the nucleons move inside a (mean ﬁeld) potential

produced by the other nucleons. In both cases discrete energy levels arise

which are ﬁlled up according to the dictates of the Pauli principle.

254 17 The Structure of Nuclei

100

0 20 40 60 80 100 120 140 160

[MeV]

> 5.0

2.5...5.0

1.0...2.5

0.5...1.0

< 0.5

126

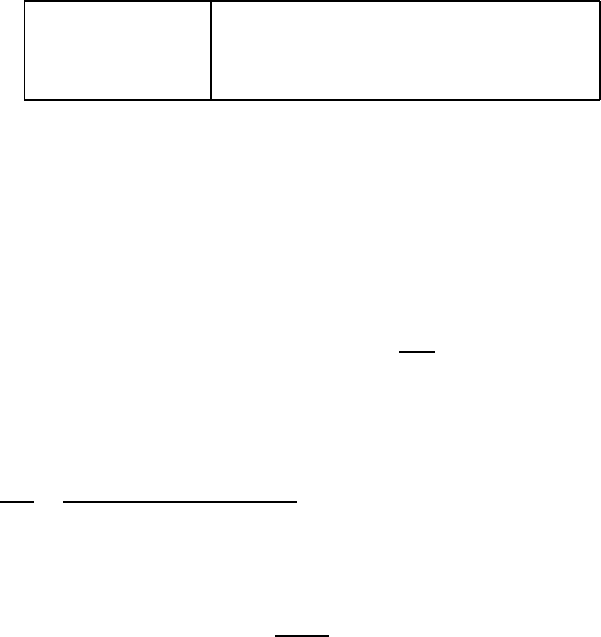
Fig. 17.5. The energy E

of the ﬁrst excited state of even-even nuclei. Note that it

is particularly big for nuclei with “magic” proton or neutron number. The excited

states generally have the quantum numbers J

. The following nuclei are

exceptions to this rule:

132

208

126

−

)and

−

). E

is small further away from the “magic” numbers –

and is generally smaller for heavier nuclei (data from [Le78]).

Magic numbers. In the atomic case we can order the electrons in “shells”.

By a shell we mean that several energy levels lie close together clearly sepa-

rated from the other states. Matters seem to be similar in nuclei.

It is an observed fact that nuclides with certain proton and/or neutron

numbers are exceptionally stable (cf. Fig. 2.4) [Ha48]. These numbers (2, 8,

20, 28, 50, 82, 126) are known as magic numbers. Nuclei with a magic proton

or neutron number possess an unusually large number of stable or very long

lived nuclides (cf. Fig. 2.2). If a nucleus has a magic neutron number, then

a lot of energy is needed to extract a neutron from it; while if we increase

the neutron number by one then the separation energy is much smaller. The

same is true of protons. It is also found that a lot of energy is needed to

excite such nuclei (Fig. 17.5).

These jumps in the excitation and separation energies for individual nu-

cleons are reminiscent of chemistry: the noble gases, i.e., those with full shells,

are particularly attached to their electrons, while the alkali metals, i.e., atoms

with just one electron in their outermost shell, have very small separation

(ionisation) energies.

The doubly magic nuclei, those with both magic proton and magic neutron

numbers, are exceptionally stable. These are the following nuclides:

208

126

17.3 The Shell Model 255

The existence of these magic numbers can be explained in terms of the so-

called shell model. For this we need ﬁrst to introduce a suitable global nuclear

potential.

Eigenstates of the nuclear potential. The wave function of the particles

in the nuclear potential can divided into two parts: a radial one R

n

(r),

which only depends upon the radius, and a part Y



(θ, ϕ) which only depends

upon the orientation (this division is possible for all spherically symmetric

potentials; e.g., atoms or quarkonium). The spectroscopic nomenclature for

quarkonium is also employed for the quantum numbers here (see p. 174):

n with



n =1, 2, 3, 4, ··· number of nodes + 1

 =s, p, d, f, g, h, ··· orbital angular momentum .

The energy is independent of the m quantum number, which can assume

any integer value between ±. Since nucleons also have two possible spin

directions, this means that the n levels are in fact 2·(2+1) times degenerate.

The parity of the wave function is ﬁxed by the spherical wave function Y



and is just (−1)



Since the strong force is so short-ranged, the form of the potential ought

to follow the density distribution of the nucleons in the nucleus. For very light

nuclei (A

∼

7) this would mean a Gaussian distribution. The potential can

then be approximated by that of a three dimensional harmonic oscillator. The

Schr¨odinger equation can be solved analytically in this particularly simple

case [Sc95]. The energy depends upon the sum N of the oscillating quanta in

all three directions as follows

harm. osc.

=(N +3/2) · ω =(N

+ N

+3/2) · ω, (17.22)

where N is related to n and  by

N =2(n − 1) + . (17.23)

Hence states with even N have positive parity and those with odd N negative

parity.

Woods-Saxon potential. The density distribution in heavy nuclei can be

described by a Fermi distribution, cf. (5.52). The Woods-Saxon potential is

ﬁtted to this density distribution:

centre

(r)=

−V

1+e

(r−R)/a

. (17.24)

States with the same N but diﬀerent n values are no longer degenerate

in this potential. Those states with smaller n and larger  are somewhat

lower. The ﬁrst three magic numbers (2, 8 and 20) can then be understood

as nucleon numbers for full shells:

256 17 The Structure of Nuclei

N 012233444···

n 1s 1p 1d 2s 1f 2p 1g 2d 3s ···

Degeneracy 2 610214618102···

States with E ≤ E

n

2 8 18 20 34 40 58 68 70 ···

This simple model does not work for the higher magic numbers. For them

it is necessary to include spin-orbit coupling eﬀects which further split the

n shells.

Spin-orbit coupling. We may formally introduce the coupling of the spin

and the orbital angular momentum (16.8) in the same manner as for the

(atomic) electromagnetic interaction. We therefore describe it by an addi-

tional s term in the potential:

V (r)=V

centr

(r)+V

s

(r)

s



. (17.25)

The combination of the orbital angular momentum  and the nucleon spin s

leads to a total angular momenta j =  ±/2 and hence to the expectation

values

s



j(j +1)− ( +1)− s(s +1)

(

/2forj =  +1/2

−( +1)/2forj =  − 1/2 .

(17.26)

This leads to an energy splitting ∆E

s

which linearly increases with the

angular momentum as

∆E

s

2 +1

·V

s

(r) . (17.27)

It is found experimentally that V

s

is negative, which means that the j =

 +1/2 is always below the j =  − 1/2 level, in contrast to the atomic case,

where the opposite occurs.

Usually the total angular momentum quantum number j =  ±1/2ofthe

nucleon is denoted by an extra index. So, for example, the 1f state is split

into a 1f

7/2

and a 1f

5/2

state. The n

level is (2j + 1) times degenerate.

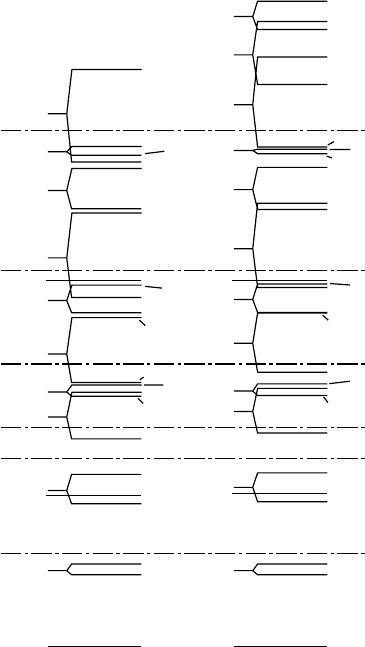
Figure 17.6 shows the states obtained from the potential (17.25). The

spin-orbit splitting is separately ﬁtted to the data for each n shell. The

lowest shells, i.e., N =0,N =1andN = 2, make up the lowest levels and

are well separated from each other. This, as we would expect, corresponds

to the magic numbers 2, 8 and 20. For the 1f shell, however, the spin-orbit

splitting is already so large that a good sized gap appears above 1f

7/2

.This

in turn is responsible for the magic number 28. The other magic numbers can

be understood in a similar fashion.

This then is the decisive diﬀerence between the nucleus and its atomic

cloud: the s coupling in the atom generates the ﬁne structure, small correc-

tions of the order of α

, but the spin-orbit term in the nuclear potential leads

17.3 The Shell Model 257

126

3/2

1/2

5/2

1/2

3/2

7/2

3/2

5/2

9/2

1/2

5/2

7/2

11/2

3/2

1/2

7/2

9/2

5/2

3/2

1/2

13/2

9/2

11/2

5/2

7/2

3/2

11/2

1/2

13/2

5/2

3/2

7/2

9/2

1/2

3/2

11/2

5/2

7/2

9/2

5/2

3/2

1/2

7/2

3/2

1/2

5/2

1/2

3/2

1/2

Protons

1/2

Neutrons

Fig. 17.6. Single par-

ticle energy levels calcu-

lated using (17.25) (from

[Kl52]). Magic numbers ap-

pear when the gaps between

successive energy shells are

particularly large. This dia-

gram refers to the nucleons

in the outermost shells.

to sizeable splittings of the energy states which are indeed comparable with

the gaps between the n shells themselves. Historically speaking, it was a

great surprise that the the nuclear spin-orbit interaction had such important

consequences [Ha49, G¨o55].

One particle and one hole states. The shell model is very successful

when it comes to explaining the magic numbers and the properties of those

nuclei with “one nucleon too many” (or too few).

Those nuclei with mass number between 15 and 17 form a particularly

attractive example of this. Their excited states are shown in Fig. 17.7. The

Nand

O nuclei are so-called mirror nuclei, i.e., the neutron number of the

one is equal to the proton number of the other and vice versa. Their spectra

are exceedingly similar, both in terms of where the levels are and also in terms

of their spin and parity quantum numbers. This is a consequence of the isospin

independence of the nuclear force: if we swap protons and neutrons the strong

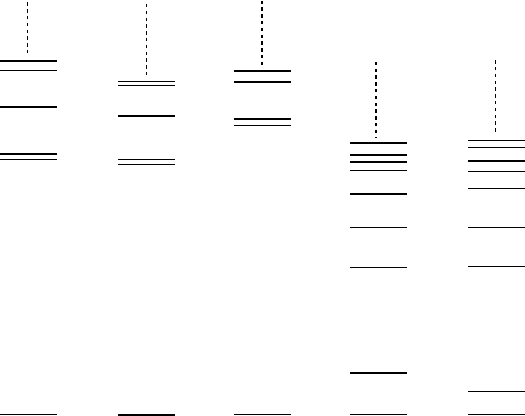
258 17 The Structure of Nuclei

force essentially does not notice it. The small diﬀerences in the spectra can

be understood as electromagnetic eﬀects. While the energy levels of

Odo

not resemble those of its neighbours, the

Oand

F nuclei are, once again,

mirror nuclei and have very similar excitation spectra. It is striking that the

nuclei with mass numbers 15 and 16 require much more energy to reach their

ﬁrst excited states than do those with mass number 17.

These spectra can be understood inside the shell model. The

O nucleus

possesses 8 protons and 8 neutrons. In the ground state the 1s

1/2

,1p

3/2

and 1p

1/2

proton and neutron shells are fully occupied and the next highest

shells, 1d

5/2

, are empty. Just as in atomic physics the angular momenta of

the particles in a full shell add up to zero and the overall parity is positive.

The ground state of

O has then the quantum numbers J

. Since the

gap between the 1p

1/2

and 1d

5/2

energy shells is quite large (about 10 MeV)

there are no easily reachable excitation levels.

The two nuclei with A= 17 both have a single extra nucleon in the 1d

5/2

shell. The spin and parity of the nucleus are completely ﬁxed by this one

nucleon. The 2s

1/2

shell happens to be just a little above the 1d

5/2

shell

and as small an energy as 0.5 MeV suﬃces to excite this single nucleon to

7.30

7.16

6.32

5.30

5.27

6.86

6.79

6.18

5.24

5.18

7.12

6.92

6.13

6.05

5.70

5.38

5.08

4.55

3.85

3.06

0.87

0.50

5.67

5.49

5.00

4.64

3.86

3.10

Fig. 17.7. Energy levels of the

Oand

F nuclei. The vertical axis

corresponds to the excitation energy of the states with the various ground states

all being set equal, i.e., the diﬀerences between the binding energies of these nuclei

are not shown.

17.3 The Shell Model 259

the next shell. The nuclear quantum numbers change from 5/2

to 1/2

this transition. The excited nucleon later decays, through photon emission,

into the lowest possible state. Just as we talk of valence electrons in atomic

physics, so these nucleons that jump between shells are known as valence

nucleons. The 1d

3/2

shell is about 5 MeV above the 1d

5/2

one and this an

amount of energy is required to reach this state.

The A = 15 ground states lack one nucleon in the 1p

1/2

shell. One speaks

of a hole and uses the notation 1p

−1

1/2

. The quantum numbers of the hole

are those of the nucleus. Thus the ground states of these nuclei have the

quantum numbers J

=1/2

−

. If a nucleon from the 1p

3/2

shell is excited

into the vacant state in the 1p

1/2

, and in some sense ﬁlls the hole, a hole is

then created in the 1p

3/2

shell. The new nuclear state then has the quantum

numbers J

=3/2

−

Magnetic moments from the shell model. If in the shell model we

associate spin and orbital angular momentum to each individual nucleon, then

we can understand the magnetic moment of the nucleus from the sum over

the nucleonic magnetic moments based upon their spin and orbital angular

momenta:

nucleus

= µ





i=1

{



+ s

} . (17.28)

Note that





1 for protons

0 for neutrons

(17.29)

and (from 6.7 etc.):



+5.58 for protons

−3.83 for neutrons.

(17.30)

Recall our ﬁve nuclei with mass numbers from 15 to 17. The magnetic

moment of

O is zero, which makes perfect sense since in a full shell the

spins and angular momenta add up to zero and so the magnetic moment

must vanish.

We are in a position to make quantitative predictions for one particle

and one hole states. We ﬁrst assume that the nuclear magnetic moment is

determined by that of the single nucleon or hole

nucleus



ψ

nucleus



 + g

s|ψ

nucleus

·µ

. (17.31)

The Wigner-Eckart theorem tells us that the expectation value of every vector

quantity is equal to its projection onto the total angular momentum, which

here means the nuclear spin J:

nucleus

= g

nucleus

· µ

J



(17.32)

260 17 The Structure of Nuclei

where

nucleus

JM



J + g

sJ|JM



JM

|JM



. (17.33)

Since the nuclear spin J in our model is nothing but the total angular mo-

mentum of our single nucleon j and we have

2j = j

+ 

− s

2sj = j

+ s

− 

(17.34)

we see that

nucleus



{j(j +1)+(+1) − s(s+1)} + g

{j(j +1)+s(s+1) − (+1)}

2j(j +1)

(17.35)

The magnetic moment of the nucleus is deﬁned as the value measured

when the nuclear spin is maximally aligned, i.e., |M

| = J. The expectation

value of J is then J and one ﬁnds

|µ

nucleus

= g

nucleus

· J =





− g



2 +1



· J for J = j =  ±

(17.36)

There are many diﬀerent ways to measure nuclear magnetic moments,

e.g., in nuclear magnetic spin resonance or from optical hyperﬁne structure

investigations [Ko56]. The experimental values [Le78] of the magnetic mo-

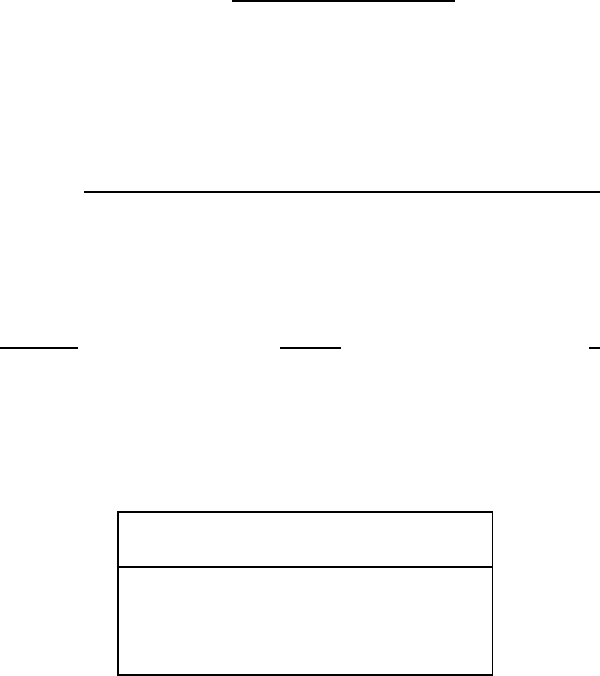
ments can be compared with the predictions of (17.36).

µ/µ

Nucleus State J

Model Expt.

Np-1p

−1

1/2

−

−0.264 −0.283

On-1p

−1

1/2

−

+0.638 +0.719

On-1d

5/2

−1.913 −1.894

Fp-1d

5/2

+4.722 +4.793

The magnetic moments of the A =15 and A =17nucleican,wesee,

be understood in a single particle picture. We should now perhaps admit to

having chosen the example with the best agreement between the model and

experiment: ﬁrstly these nuclei are, up to one single nucleon or hole, doubly

magic and secondly they have a relatively small nucleon number which means

that eﬀects such as polarisation of the remainder by the valence nucleon are

relatively tiny.

We assume for nuclei with odd mass number whose incomplete shells con-

tain more than one nucleon or hole that the total nucleon magnetic moment

is due to the one unpaired nucleon [Sc37]. The model then roughly repro-

duces the experimental trends, but disagreements as big as ±1µ

and larger

appear for many nuclei. The magnetic moment is, generally speaking, smaller

than expected. The polarisation of the rest of the nucleus from the unpaired

nucleon tends to explain this [Ar54].

17.4 Deformed Nuclei 261

17.4 Deformed Nuclei

The shell model approximation which assumes that nuclei are spherically

symmetric objects – plus, of course, the additional spin-orbit interaction – is

only good for those nuclei which are close to having doubly magic full shells.

For nuclei with half full shells this is not the case. In such circumstances the

nuclei are deformed and the potential is no longer spherically symmetric.

It was already realised in the 1930’s, from atomic spectroscopy, that nuclei

are not necessarily always spherical [Ca35, Sc35]. Deviations in the ﬁne struc-

ture of the spectra hinted at a non-vanishing electrical quadrupole moment,

i.e. that the charge distribution of the nuclei was not spherically symmetric.

Quadrupole moments. The charge distribution in the nucleus is described

in terms of electric multipole moments. Since the odd moments (e.g., the

dipole and octupole) have to vanish because of parity conservation, the elec-

tric quadrupole moment is the primary measure of in how far the charge

distribution, and hence the nucleus, deviate from being spherical.

The classical deﬁnition of a quadrupole moment is

Q =





− x



(x)d

x. (17.37)

An ellipsoid of diameter 2a in the z direction and diameter 2b in the other

two directions (Fig. 3.9), with constant charge density (x) has the following

quadrupole moment:

Q =



− b



. (17.38)

For small deviations from spherical symmetry, it is usual to introduce a

measure for the deformation. If the average radius is R  =(ab

)

1/3

and the

diﬀerence is ∆R = a −b then the quadrupole moment is proportional to the

deformation parameter

δ =

∆R

R 

(17.39)

and we ﬁnd

Q =

ZeR 

δ. (17.40)

Since the absolute value of a quadrupole moment depends upon the charge

and size of the nucleus concerned, we now introduce the concept of the reduced

quadrupole moment to facilitate the comparison of the deformations of nuclei

with diﬀerent mass numbers. This is a dimensionless quantity and is deﬁned

as the quadrupole moment divided by the charge Ze and the square of the

average radius R :

We skip over the exact deﬁnition of the deformation parameter here; (17.38) and

(17.39) are approximations for small deformations.