Povh B., Rith K., Scholz Ch., Zetsche F. Particles and Nuclei: An Introduction to the Physical Concepts

Подождите немного. Документ загружается.

136 10 Phenomenology of the Weak Interaction

The muon mass and lifetime have been measured to a high precision:

= (105.658 389 ± 0.000 034) MeV/c

=(2.197 035 ± 0.000 040) · 10

−6

s . (10.6)

This yields a value for the Fermi constant

(c)

=(1.166 39 ± 0.000 01) · 10

−5

GeV

−2

. (10.7)

Neutrino-electron scattering. Neutrino-electron scattering is a reaction

between free, elementary particles. It proceeds exclusively through the weak

interaction. We can discuss the eﬀects of the eﬀective coupling strength G

on the cross-section of this reaction and show why the weak interaction is

called “weak”.

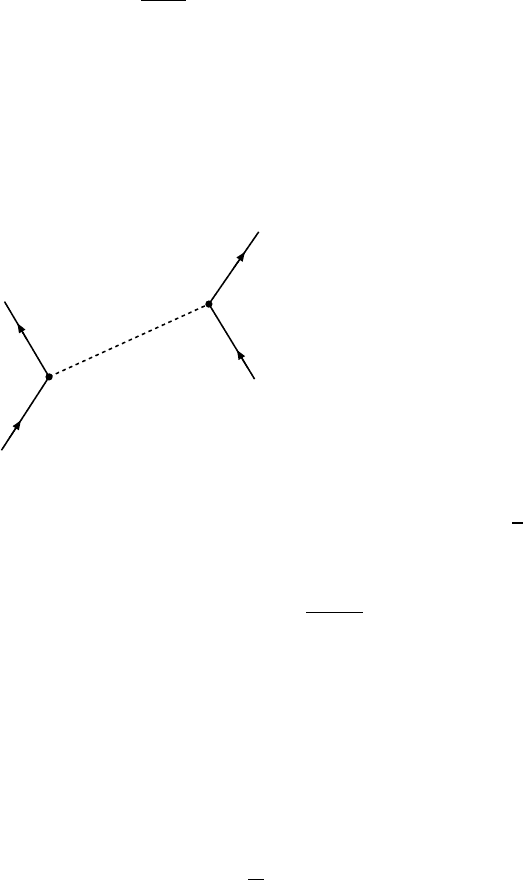
In the diagram below the scattering of muon-neutrinos oﬀ electrons in

which the ν

is changed into a µ

−

is shown.

We have chosen this process as our



example since it can only take place

via W-exchange. Calculating ν

-e

−

scattering is more complicated since

both Z- and W-exchange lead to the

same ﬁnal state and thus interfere

with each other.

For small four-momenta the total

cross-section for neutrino-electron

scattering is proportional to the

square of the eﬀective coupling con-

stant G

. Similarly to our discussion of the total cross-section in e

−

annihilation in Sect. 9.1, the characteristic length and energy scales of the

reaction (the constants c and the centre of mass energy

√

s)mustenterthe

cross-section in such a way as to yield the correct dimensions ([area]):

σ =

π(c)

· s, (10.8)

where s may be found in the laboratory frame from (9.3) to be s =2m

From (10.7) one ﬁnds that the cross-section in the laboratory frame is:

lab

=1.7 · 10

−41

· E

/GeV. (10.9)

This is an extremely tiny cross-section. To illustrate this point we now es-

timate the distance L which a neutrino must traverse until it weakly interacts

with an electron. The electron density in iron is

N

≈ 22 · 10

−3

. (10.10)

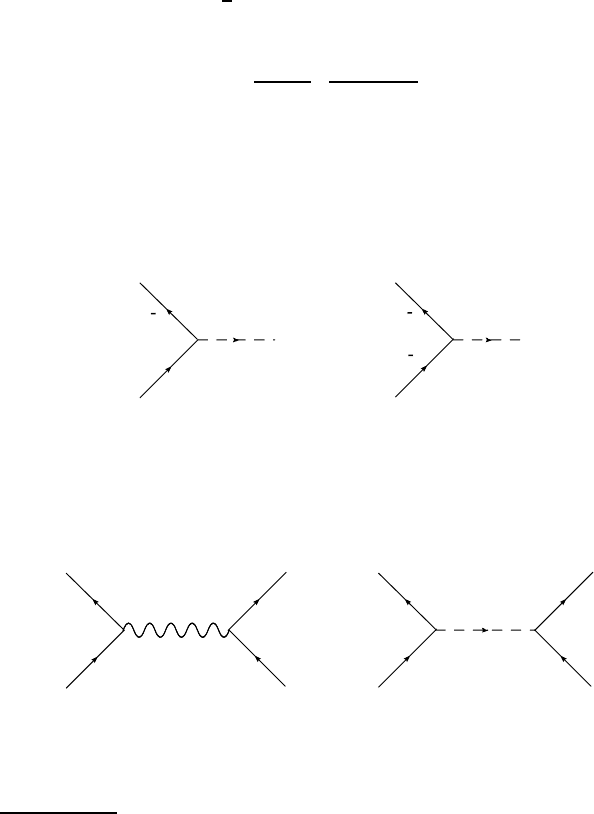
10.3 Coupling Strength of the Weak Interaction 137

Neutrinos produced in the sun via hydrogen fusion have typically an energy of

around 1 MeV. Their mean free path is therefore L =(n

·σ)

−1

=2.6·10

which is about 30 light years!

At very high energies the simple formula (10.9) is no longer valid, since the

cross-section would limitlessly grow with the neutrino energy. This of course

will not happen in practise: at large four momentum transfers Q

 M

the propagator term primarily determines the energy dependence of the cross-

section. A point-like interaction approximation no longer holds. At a ﬁxed

centre of mass energy

√

s the cross-section falls oﬀ, as in electromagnetic

scattering, as 1/Q

. The total cross-section is on the other hand:

σ =

π(c)

s + M

· s. (10.11)

The cross-section does not then increase linearly with s, as the point-like

approximation implies, rather it asymptotically approaches a constant value.

Neutral currents. Up to now we have only considered neutrino-electron

scattering via W

exchange, i.e., through charged currents (left side of the

ﬁgure). The W

carries away the positive charge and transforms the electron-

neutrino to an electron. Neutrinos and electrons can, however, interact via

-exchange, i.e., neutral current interactions are possible (right side of the

ﬁgure). The Z

transforms neither charge nor mass.

In general case the interactions via neutral currents will be hard to ob-

serve as they are masked by much stronger electromagnetic and in the case of

quarks by strong interaction. In the electron-electron scattering one has a su-

perposition of the electromagnetic and weak interaction The strength of neu-

tral currents and electromagnetic interaction become comparable ﬁrst at the

centre of mass energy on the order of the Z

mass. The interference between

the neutral currents end the electromagnetic interaction has been beautifully

demonstrated in experiments at the electron-positron collider LEP at CERN.

The absorption of neutrinos by the atomic nuclei is neglected here. This is a

reasonable approximation for neutrino energies less than 1 MeV, but would need

to be modiﬁed for higher energies.

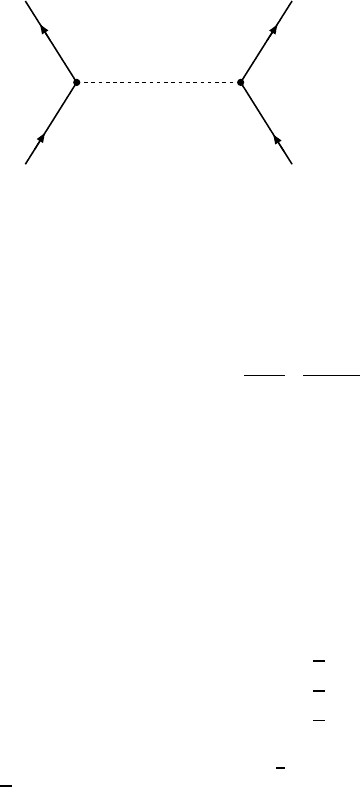
138 10 Phenomenology of the Weak Interaction

Elastic muon-neutrino scattering oﬀ electrons. The muon-neutrino

scattering oﬀ electrons is particularly suitable for investigating the weak in-

teraction via Z

-exchange. This is because conservation of lepton family num-

ber precludes W-exchange. Reactions of this kind were ﬁrst seen in 1973 at

CERN [Ha73] and was the ﬁrst experimental signal for weak neutral currents.



−

→ ν

−

Let us estimate the total cross section for ν

−

→ ν

−

for small four-

momenta (10.8). We just repeat the calculation we did for the scattering via

charged currents but modifying the coupling G

. The only diﬀerence between

the two interactions is in the mass of the two exchange bosons. The mass of

the exchange boson squared appears in the propagator, so that the G

should

be multiplied by M

≈ 0.78. The total cross section at low energies

reads then

σ =

π(c)

· s, (10.12)

σ(ν

−

→ ν

−

) ≈ 0.6 · σ(ν

e → µ

−

) . (10.13)

Universality of the weak interaction. If we assume that the weak charge

g is the same for all quarks and leptons, then (10.5) must hold for all possible

charged decays of the fundamental fermions into lighter leptons or quarks.

All the decay channels then contribute equally, up to a phase space correction

coming from the diﬀerent masses, to the total decay width.

We choose to consider the example of the decay of the τ-lepton. This

particle has essentially three routes open to it

−

→ ν

+ ν

−

→ ν

+ ν

+ µ

−

→ ν

+ u + d (10.14)

whose widths are Γ

τe

≈ Γ

τµ

and Γ

τdu

≈ 3Γ

τµ

. The factor of three follows from

the

ud-pair appearing in three diﬀerent colour combinations (r¯r, b

b, g¯g). The

weak decay-branch with the strange quark was neglected in this estimate.

From the mass term in (10.5) we have:

τe

=(m

)

· Γ

µe

, (10.15)

and the lifetime is thus predicted to be:

10.4 The Quark Families 139



τe

+ Γ

τµ

+ Γ

τd

≈

5 · (m

)

≈ 3.1 · 10

−13

s . (10.16)

Experimentally we ﬁnd [PD98]

exp

=(2.900 ± 0.012) · 10

−13

s . (10.17)

This good agreement conﬁrms that quarks occur in three diﬀerent colours and

is strongly supportive of the quark and lepton weak charges being identical.

10.4 The Quark Families

We have claimed that the weak charge is universal, and that all the weak

reactions which proceed through W exchange can therefore be calculated

using the one coupling constant g or G

. The lifetime of the τ-lepton seemed

to illustrate this point: our expectations, based on the assumption that the

W boson couples with the same strength to both quarks and leptons were

fulﬁlled. However, the lifetime does not contain the decay widths for leptonic

and hadronic processes separately, but only their sum. Furthermore it is very

sensitive to the mass of the τ-lepton. Hence, this is not a particularly precise

test of weak charge universality.

The coupling to quarks can be better determined from semi-leptonic

hadron decays. This yields a smaller value for the coupling than that ob-

tained from muon data. If a d-quark is transformed into a u-quark, as in

the β-decay of the neutron, the coupling constant appears to be about 4 %

smaller. In processes in which an s-quark is transformed into a u-quark, as

in Λ

decay, it even appears to be 20 times smaller.

The Cabibbo angle. An explanation of these ﬁndings was proposed by

Cabibbo as early as 1963 [Ca63], at a time at which quarks had not been

introduced. We will re-express Cabibbo’s hypothesis in modern terms. We

may group the quarks into families, according to their charges and masses:







Quark transitions in the weak decays in fact are observed predominantly

within a family but, to a lesser degree, from one family to another. To ac-

count for the transitions between the families one has chosen to deﬁne as the

“partner” of the ﬂavour eigenstate |u a state |d, which is a linear combina-

tion of |d and |s. Similarly the partner of the c-quark is a linear combination

of |s and |d, orthogonal to |d



,whichwecall|s



.

The coeﬃcients of these linear combinations can be written as the cosine

and sine of an angle called the Cabibbo angle θ

. The quark eigenstates |d





and |s



 of W exchange are related to the eigenstates |d and |s of the strong

interaction, by a rotation through θ

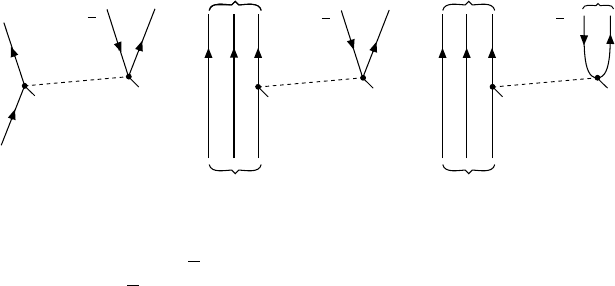
140 10 Phenomenology of the Weak Interaction



 =cosθ

|d  +sinθ

|s 



 =cosθ

|s −sin θ

|d  , (10.18)

which may be written as a matrix:















cos θ

sin θ

−sin θ

cos θ





|d 

|s 



. (10.19)

Whether the state vectors |d and |s or the state vectors |u and |c are

rotated, or indeed both pairs simultaneously, is a matter of convention alone.

Only the diﬀerence in the rotation angles is of physical importance. Usually

the vectors of the charge −1/3 quarks are rotated while those of the charge

+2/3 quarks are left untouched.

Experimentally, θ

is determined by comparing the lifetimes and branch-

ing ratios of the semi-leptonic and hadronic decays of various particles as

shown in the sketch. This yields:

sin θ

≈ 0.22 , and cos θ

≈ 0.98 . (10.20)

The transitions c ↔ dands↔ u, as compared to c ↔ sandd↔ u, are

therefore suppressed by a factor of

sin

:cos

≈ 1:20. (10.21)

–

cos T

sinT

–

cos T

ddu

sdu

–

cosT

sinT

–

We can now make our treatment of τ decay more precise. In (10.14), we

stated that τ → ν

+ u + d is “essentially” the only hadronic decay of the τ .

But τ → ν

+ u + s is also energetically possible. Whereas the former decay

is only slightly suppressed by a factor of cos

, the latter is faced with a

factor of sin

. However, since cos

and sin

add to one our conclusion

concerning the lifetime of the τ-lepton is not aﬀected, as long as we ignore

the diﬀerence in the quark masses.

The Cabibbo-Kobayashi-Maskawa matrix. Adding the third generation

of quarks, the 2 × 2 matrix of (10.19) is replaced by a 3 × 3 matrix [Ko73].

This is called the Cabibbo-Kobayashi-Maskawa matrix (CKM matrix):

10.4 The Quark Families 141

⎛

⎝













⎞

⎠

⎛

⎝

⎞

⎠

⎛

⎝

|d 

|s 

|b 

⎞

⎠

. (10.22)

The probability for a transition from a quark q to a quark q



is proportional

to |V



, the square of the magnitude of the matrix element.

The matrix elements are by now rather well known [Ma91]. They are

correlated since the matrix is unitary. The total number of independent pa-

rameters is four: three real angles and an imaginary phase. The phase af-

fects weak processes of higher order via the interference terms. CP violation

(cf. Sect. 14.4) is attributed to the existence of this imaginary phase [Pa89].

The following numbers represent the 90 %–conﬁdence limits on the mag-

nitudes of the matrix elements [PD98]:





⎛

⎜

⎝

0.9745 ···0.9760 0.217 ···0.224 0.0018 ···0.0045

0.217 ···0.224 0.9737 ···0.9753 0.036 ···0.042

0.004 ···0.013 0.035 ···0.042 0.9991 ···0.9994

⎞

⎟

⎠

. (10.23)

The diagonal elements of this matrix describe transitions within a family;

they deviate from unity by only a few percent. The values of the matrix

elements V

and V

are nearly one order of magnitude smaller than those of

and V

. Accordingly, transitions from the third to the second generation

(t → s, b → c) are suppressed by nearly two orders of magnitude compared

to transitions from the second to the ﬁrst generation. This applies to an even

higher degree for transitions from the third to the ﬁrst generation. The direct

transition b → u was detected in the semi-leptonic decay of B mesons into

non-charmed mesons [Fu90, Al90, Al91].

Weak quark decays only proceed through W exchange. Neutral currents

which change the quark ﬂavour (e. g., c → u) have thus far not been observed

and are taken to be zero.

142 10 Phenomenology of the Weak Interaction

10.5 The Lepton families

The leptonic ﬂavor mixing matrix. As indicated out above, neutrino os-

cillations show that neutrinos have non-vanishing masses and that the ﬂavour

families |ν

, |ν

 and |ν

, which are eigenstates of the weak interaction, are

not eigenstates of the mass operator which we write as ν

, ν

and ν

.The

neutrino eigenstates of the weak interaction are a superposition of the mass

eigenstates in a similar way to d



and b



being a superposition of the

strong interaction eigenstates d, s and b. Remember, the mass eigenstates are

the constant of the motion and because they diﬀer, the relative phases of

these components change with time. In analogy to the CKM matrix, we can

introduce a unitary 3×3 matrix relating the neutrino weak eigenstates to the

mass eigenstates:

⎛

⎝

|ν



|ν



|ν



⎞

⎠

⎛

⎝

µ1

µ2

µ3

τ1

τ2

τ3

⎞

⎠

⎛

⎝

|ν



|ν



|ν



⎞

⎠

. (10.24)

In this matrix (10.24) we have replaced the V ’s of 10.22 by U’s, the d’, s’

and b’byν

, ν

and ν

and also d, s and b by ν

,ν

and ν

A possible neutrino mixing has been theoretically studied prior to the

observed neutrino oscillation. B. Pontecorvo was the ﬁrst to consider the

possibility of neutrino-antineutrino oscillations ([Po57]). Maki, Nakagawa and

Sakata discussed a possible ﬂavour mixing for neutrinos ([Ma62]).

The values of the matrix elements U

are deduced from the observed

neutrino oscillations. To keep the discussion as simple as possible, we will

do this for just two neutrino ﬂavours and ask what happens to the solar

neutrinos after they have traveled for a time t. The time dependent wave

function of the electron neutrino is

|ν

(t)  = U

−iE

t/

|ν

 + U

−iE

t/

|ν

. (10.25)

Neutrinos are relativistic and their energy can be approximated by



+ m

≈ pc





. (10.26)

The probability of ﬁnding an electron neutrino after time t in the beam is

then

→ν

(t)=ν

(t)|ν

(t)=|U

+|U

+2|U

||U

|cos

)



− m



pc

(10.27)

From the observed oscillations one can obtain ∆m

= m

− m

if one

measures the oscillation length, L. This is the distance when the phase of the

cosine in (10.27) becomes 2π and it takes place at the time t = L/c:

10.5 The Lepton families 143

L =4π

pc

∆m

. (10.28)

The best present estimate from solar neutrinos is 0.5 · 10

−5

∆m

SUN

< 2 ·10

−4

. The oscillation length for the atmospheric neutri-

nos gives the following limits: 1.4·10

−3

<∆m

AT M

< 5.1·10

−3

We identify ∆m

SUN

= ∆m

and ∆m

AT M

= |∆m

| = |∆m

Strong attenuations observed in the solar and the atmospheric neutrino

ﬂuxes mean that the neutrinos of diﬀerent ﬂavours mix strongly. Taking into

account all the experimental constraints dictated by the present oscillation

measurements, the best-ﬁt value of the leptonic mixing matrix U is [Gi03]

U =

⎛

⎝

−0.83 0.56 0.00

0.40 0.59 0.71

0.40 0.59 −0.71

⎞

⎠

. (10.29)

In (10.29) we omitted the large errors of single matrix elements as we

want to show only the main features of the leptonic mixing matrix.

Such a matrix, with all elements being large (except U

) is called “bi-

large”. It is very diﬀerent from the quark mixing matrix, in which the mixing

is very small. Such a diﬀerence in the quark and leptonic mixing might be

an important piece of information for our understanding of the physics be-

yond the Standard Model (19.4), which presumably involves some sort of

quark-lepton uniﬁcation.

Following B. Kayser ([Ka05]) the main features of the leptonic ﬂavor

mixing matrix can be presented graphically (Fig. 10.2) by approximating the

ﬂavor-j fraction of each mass eigenstate i by the square of the matrix element

(10.29).

Fig. 10.2. A tree-neutrino squared-mass spectrum that accounts for the observed

ﬂavor mixing of solar, reactor, and atmospheric neutrinos. The ν

fraction of each

mass state is crosshatched, the ν

fraction is indicated by by right-leaning hatching,

and the ν

fraction by the left-leaning hatching

144 10 Phenomenology of the Weak Interaction

10.6 Majorana Neutrino?

The charged leptons and quarks are Dirac particles as the consequence of

their electric charge. Charged fermions and their antifermions have to have

the same mass. Consequently, the charged fundamental fermions obey the

four component Dirac equation.

The neutrinos are neutral and as there is no explicit lepton number con-

servation, their mass eigenstates can be a superposition of particles and an-

tiparticles. There is no a priori reason not to consider the possibility that the

neutrinos that we observe are not the Dirac neutrinos and the antineutrinos,

but the two helicity states of the same particle, named Majorana neutrino.

Majorana neutrinos are their own antiparticles. This scenario has been sug-

gested by Majorana long time ago.

The counterpart of the light Majorana neutrinos would be heavy neutri-

nos. In the Standard Model of Elementary Particles (Chap.12) it is expected

that the mechanism responsible for giving quarks and leptons their masses

would give the fermions of one particle family masses on the same order of

magnitude, to quarks and to leptons masses M

≈ M

= M

q,l

. In some exten-

sions of the Standard Model, it is natural for the masses of the light neutrinos

and the heavy neutrinos M

to be related to the Dirac mass M

q,l

≈ M

q,l

. (10.30)

The interpretation of this relation is the following: Neutrinos got ﬁrst the

Dirac mass M

q,l

, on the same order as the charged fermions, with neutrinos

and antineutrinos degenerate in mass. Because the lepton number is explicitly

not conserved, the particles and antiparticles can mix, and the degeneracy

was removed in one of many phase transitions of the early universe. The light

Majorana neutrinos were pushed way down in the mass, the heavy way up.

This scenario with the Majorana neutrino is appealing to theorists for

many reasons. It explains why the neutrinos have many orders of magni-

tude smaller masses than the charged fermions, the lepton number non-

conservation, and probably CP violation in the decay of the heavy Majo-

rana neutrinos, could help to explain how it came to the matter antimatter

asymmetry in the early history of the universe.

Unfortunately, at present it seems that there is just one experiment that

can decide on the nature of the neutrino, the neutrinoless double beta decay,

we will discuss in section 17.7.

10.7 Parity Violation

A property unique to the weak interaction is parity violation. This means

that weak interaction reactions are not invariant under space inversion.

An example of a quantity which changes under a spatial inversion is he-

licity

10.7 Parity Violation 145

h =

s · p

|s|·|p|

, (10.31)

which we introduced in Sect. 5.3. The numerator is a scalar product of an

axial vector (spin) and a vector (momentum). Whereas spin preserves its ori-

entation under mirror reﬂection, the direction of the momentum is reversed.

Thus helicity is a pseudoscalar, changing sign when the parity operator is

applied to it. An interaction which depends upon helicity is therefore not

invariant under spatial reﬂections.

In general, the operator of an interaction described by the exchange of a

spin-1 particle can have a vector or an axial vector nature. In order for an

interaction to conserve parity, and therefore to couple identically to both right

and left-handed particles, it must be either purely vectorial or purely axial. In

electromagnetic interactions, for example, it is experimentally observed that

only a vector part is present. But in parity violating interactions, the matrix

element has a vector part as well as an axial vector part. Their strengths

are described by two coeﬃcients, c

and c

. The closer the size of the two

parts the stronger is the parity violation. Maximum parity violation occurs

if both contributions are equal in magnitude. A (V + A)–interaction, i. e.,

a sum of vector and axial interactions of equal strength (c

= c

), couples

exclusively to right-handed fermions and left-handed antifermions. A (V−A)–

interaction (c

=−c

) only couples to left-handed fermions and right-handed

antifermions.

As we will show, the angular distribution of electrons produced in the

decay of polarised muons exhibits parity violation. This decay can be used

to measure the ratio c

. Such experiments yield c

=−c

=1 for the cou-

pling strength of W bosons to leptons. One therefore speaks of a V-minus-A

theory of charged currents. Parity violation is maximal. If a neutrino or an

antineutrino is produced by W exchange, the neutrino helicity is negative,

while the antineutrino helicity is positive. In fact all experiments are consis-

tent with neutrinos being always left-handed and antineutrinos right-handed.

We will describe such an experiment in Sect. 17.6.

For massive particles β = v/c < 1 and the above considerations must be

modiﬁed. On the one hand, massive fermions can be superpositions of right-

handed and of left-handed particles. On the other hand, right-handed and

left-handed states receive contributions with the opposite helicity, which in-

crease the more β decreases. This is because helicity is only Lorentz-invariant

for massless particles. For particles with a non-vanishing rest mass it is al-

ways possible to ﬁnd a reference frame in which the particle is “overtaken”,

i.e., in which its direction of motion and thus its helicity are reversed.

CP conservation. It may be easily seen that if the helicity of the neutrinos

is ﬁxed, then C-parity (“charge conjugation”) is simultaneously violated. Ap-

plication of the C-parity operator replaces all particles by their antiparticles.

Thus, left-handed neutrinos would be transformed into left-handed antineu-

trinos, which are not found in nature. Therefore physical processes which