Попечителев Е.П. Кореневский Н.А. Электрофизиологическая и фотометрическая медицинская техника: Теория и проектирование

Подождите немного. Документ загружается.

нии ЦАП с большим числом разрядов обычно используют матрицы лест-

ничного типа R-2R.

В схемах лестничного типа номиналы резисторов относятся

2г1, -при-

чем схемы соединений резисторов таковы, что вклад каждого разряда

пропорционален его двоичному весу. На рис. 9.100, б показана основная

структура такого ЦАП. So—ключ, замыкающий старший разряд,

S„-i — младший, при поступлении единицы только в старшем разряде

ключ

подключает опорное напряжение к резистору 2R, подключенно-

му к точке

а.

Все остальные резисторы своими ключами замкнуты на зем-

лю. Их эквивалентное сопротивление относительно точки а (все резисто-

ры слева от а) составляет 2R, поэтому на неинвертирующий вход ОУ по-

ступает сигнал Uo/2. Такие же эквивалентные сопротивления 2R с левой

стороны имеют место и для точки б и т. д. Если к

подключен резистор

2R только через ключ S

то

точке

будет напряжение U

/2, но относите-

льно ОУ это напряжение передается через резистор R, таким образом, на

вход ОУ попадает сигнал Uo/4, что соответствует весу второго разряда.

Если подключен резистор только через

S2,

то на

ОУ

попадет сигнал U

/8 и

т. д. Поскольку ОУ работает в режиме повторителя с коэффициентом пе-

редачи «единица», то для него можно записать [7]

вых

=и

Ха

(

2'.

i=0

Достоинством такого ЦАП является использование сопротивлений

только двух номиналов, что легко реализуется в интегральном исполне-

нии. В практических схемах интегральных ЦАП часто используют соче-

тание токовых матриц со взвешенными резисторами

матриц типа R-2R.

Аналоговые ключи преобразователей выполняются на базе биполяр-

ных

униполярных транзисторов. Для униполярных транзисторов харак-

терна отсутствие остаточного напряжения во включенном состоянии,

кроме того, на их основе можно строить ключи, коммутирующие напря-

жение произвольной полярности, используя источники опорного напря-

жения любой полярности и любого уровня напряжения. Для получения

лучших соотношений сигнал/шум в ЦАП рекомендуется эталонное на-

пряжение U

выбирать как можно большим. Такой ЦАП интерпретируют

еще и как схему аналого-цифрового перемножения сигналов (схема на

рис. 9.100, в),и как управляемый двоичным кодом коэффициент передачи

(цифровой потенциометр).

При преобразовании кода в разнополярный аналоговый сигнал обыч-

но учитывают три способа представления чисел со знаком: использова-

ние в цифровом коде специального знакового разряда; использование

смещенного кода; использование дополнительного кода [6].

358

В первом простейшем

способе для обозначения зна-

ка используется один двоич-

ный разряд, например

тог-

да в зависимости от значения

этого разряда с помощью

ключа К обеспечивают ин-

версию выходного сигнала

ЦАП, например так, как это

показано на рис. 9.101, а.

Здесь квадрат со значками

#/А — одно из условных обо-

значений ЦАП на структур-

ных схемах.

При смещенном коде

число 0 соответствует поло-

вине шкалы обычного двоич-

ного кода. Справа по шкале отсчитываются (по возрастанию модуля) по-

ложительные числа, слева по шкале, так же по возрастанию моду-

ля, — отрицательные числа. Смещенный код подается на

ЦАП

как обыч-

ный двоичный код, а выходное напряжение ЦАП сдвигается на половину

шкалы в область отрицательных значений напряжений (рис. 9.101, б).

При использовании дополнительного кода отрицательное число образу-

ется инверсией всех разрядов соответствующего по модулю положитель-

ного числа, с последующим прибавлением единицы к младшему разряду.

Схема, реализующая такое преобразование, приведена на рис. 9.101, в.

Отличие

от ЦАП,

работающего со смещенным кодом, заключается в том,

что старший разряд перед подачей на ЦАП инвертируется.

При выборе конкретных схем ЦАП и АЦП для построения биотехни-

ческих систем ориентируются на их технические характеристики.

К основным характеристикам относят разрешающую способность,

время преобразования t

, точность преобразования и номинальный вы-

ходной ток

ВЬ1Х

Разрешающая способность определяется числом разря-

дов преобразуемого кода — п. Теоретически ЦАП должен обеспечивать

различных значений выходного сигнала, различающихся друг от друга

точно на величину уровня разрешения

Различного рода погрешно-

сти, вызванные неидеальностью ключей, температурной нестабильно-

стью элементов, нелинейными явлениями, приводят к отличию реально-

го значения разрешающей способности

от

теоретического. В большинст-

ве

случаев разработчики ЦАП стремятся к тому, чтобы

все

составляющие

погрешностей в совокупности не приводили к появлению абсолютной

359

и.

S,„. : J)

ША

J 't и

U.-

^-••••'Vi —£

ША

,0,5U„

Ц,

s, s„.

43-

MIA

0.5U,

•U„

в)

Рис. 9.101. Схема получения разнополярных

сигналов

погрешности, превышающей

уровень разрешения преобра-

зователя, или в пересчете на

цифровой код ±0,5 единицы

младшего разряда [6].

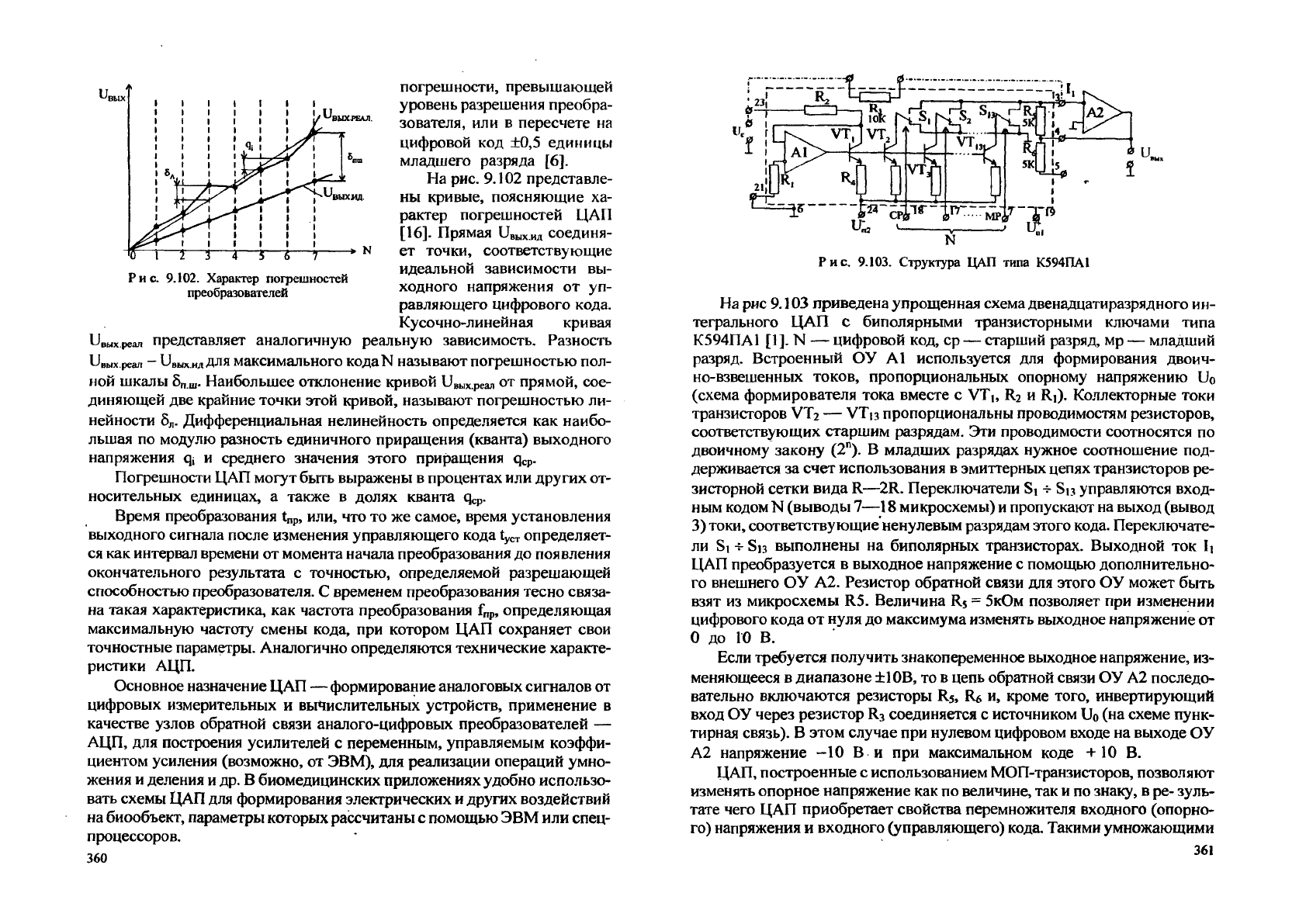
На рис. 9.102 представле-

ны кривые, поясняющие ха-

рактер погрешностей ЦАП

[16]. Прямая и

вых

ид

соединя-

ет точки, соответствующие

идеальной зависимости вы-

ходного напряжения от уп-

равляющего цифрового кода.

Кусочно-линейная кривая

и,,ыхреал представляет аналогичную реальную зависимость. Разность

Пвых.реал - Ц>ых.идДля максимального

KoflaN

называют погрешностью пол-

ной шкалы б

пш

. Наибольшее отклонение кривой и

вых

реа

л от прямой, сое-

диняющей две крайние точки этой кривой, называют погрешностью ли-

нейности 8

. Дифференциальная нелинейность определяется как наибо-

льшая по модулю разность единичного приращения (кванта) выходного

напряжения q, и среднего значения этого приращения q

Погрешности ЦАП могут

быть

выражены в процентах или других от-

носительных единицах, а также в долях кванта q

Время преобразования t

, или, что то же самое, время установления

выходного сигнала после изменения управляющего кода

определяет-

ся как интервал времени от момента начала преобразования до появления

окончательного результата с точностью, определяемой разрешающей

способностью преобразователя. С временем преобразования тесно связа-

на такая характеристика, как частота преобразования f

, определяющая

максимальную частоту смены кода, при котором ЦАП сохраняет свои

точностные параметры. Аналогично определяются технические характе-

ристики АЦП.

Основное назначение ЦАП—формирование аналоговых сигналов от

цифровых измерительных и вычислительных устройств, применение в

качестве узлов обратной связи аналого-цифровых преобразователей —

АЦП, для построения усилителей с переменным, управляемым коэффи-

циентом усиления (возможно, от ЭВМ), для реализации операций умно-

жения и деления и

др.

В биомедицинских приложениях удобно использо-

вать схемы ЦАП для формирования электрических

других воздействий

на биообъект, параметры которых рассчитаны с помощью ЭВМ или спец-

процессоров.

360

Рис. 9.102. Характер погрешностей

преобразователей

На рис 9.103 приведена упрощенная схема двенадцатиразрядного ин-

тегрального ЦАП с биполярными транзисторными ключами типа

К594ПА1 [1]. N — цифровой код, ср — старший разряд, мр — младший

разряд. Встроенный ОУ А1 используется для формирования двоич-

но-взвешенных токов, пропорциональных опорному напряжению Uo

(схема формирователя тока вместе с VT

и Ri). Коллекторные токи

транзисторов VT

— VTB пропорциональны проводимостям резисторов,

соответствующих старшим разрядам. Эти проводимости соотносятся по

двоичному закону (2

). В младших разрядах нужное соотношение под-

держивается за счет использования в эмиттерных цепях транзисторов ре-

зисторной сетки вида R—2R. Переключатели Si

-s- S13

управляются вход-

ным кодом N (выводы 7—18 микросхемы)

пропускают на выход (вывод

токи, соответствующие ненулевым разрядам этого

кода.

Переключате-

ли S1-S-S13 выполнены на биполярных транзисторах. Выходной ток Ь

ЦАП преобразуется в выходное напряжение с помощью дополнительно-

го внешнего ОУ А2. Резистор обратной связи для этого ОУ может быть

взят из микросхемы R5. Величина

= 5кОм позволяет при изменении

цифрового кода от нуля до максимума изменять выходное напряжение от

0 до 10 В.

Если требуется получить знакопеременное выходное напряжение, из-

меняющееся в диапазоне ±10В, то в цепь обратной связи ОУ А2 последо-

вательно включаются резисторы R5, R6 и, кроме того, инвертирующий

вход ОУ через резистор R

соединяется с источником

(на схеме пунк-

тирная связь). В этом случае при нулевом цифровом входе на выходе ОУ

А2 напряжение -10 В и при максимальном коде + 10 В.

ЦАП, построенные с использованием МОП-транзисторов, позволяют

изменять опорное напряжение как по величине, так

по знаку, в ре- зуль-

тате чего ЦАП приобретает свойства перемножителя входного (опорно-

го) напряжения и входного (управляющего) кода. Такими умножающими

361

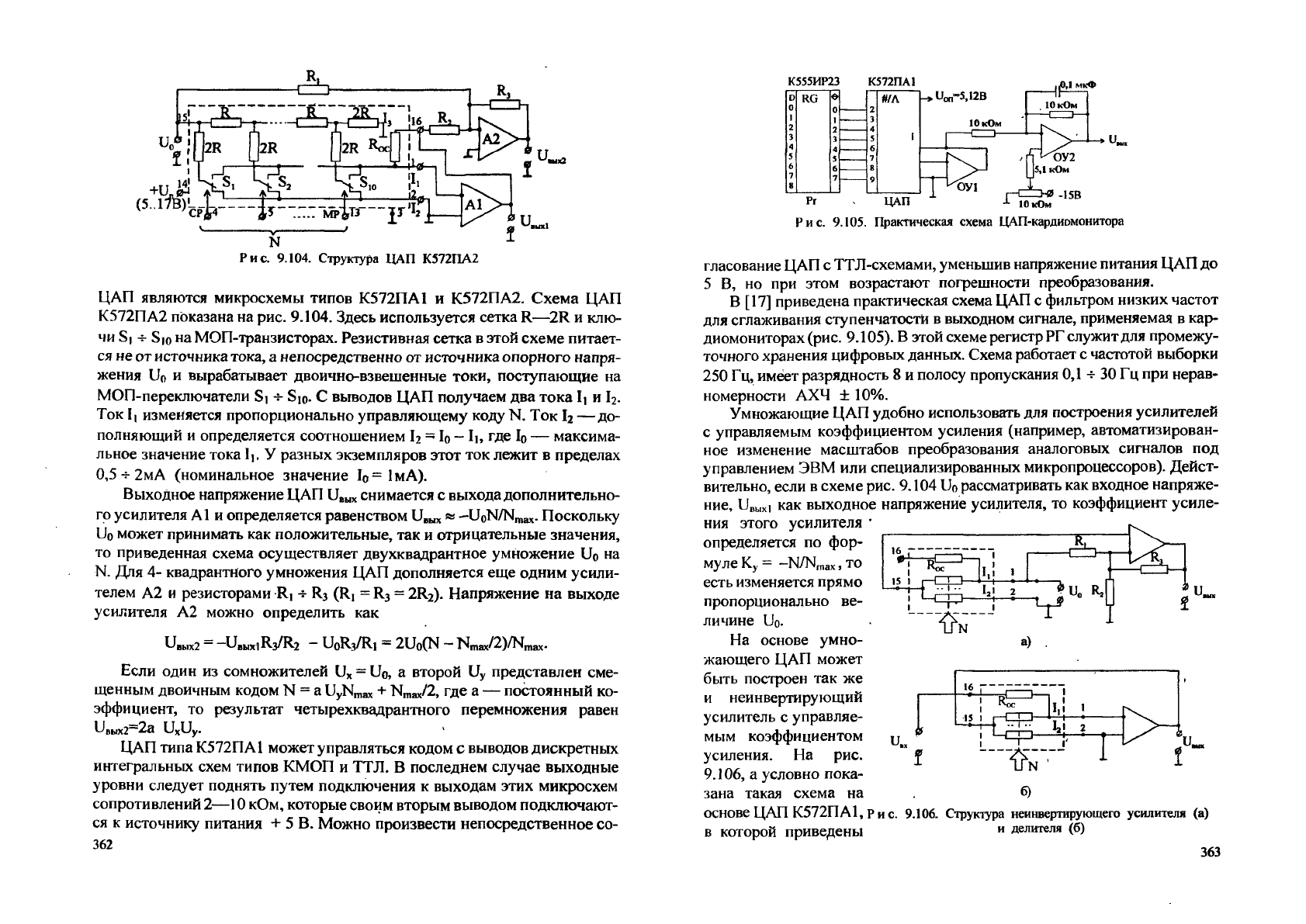
Рис. 9.104. Структура ЦАП К572ПА2

ЦАП являются микросхемы типов К572ПА1 и К572ПА2. Схема ЦАП

К572ПА2 показана на рис. 9.104. Здесь используется сетка R—2R и клю-

чи S| + Sio на МОП-транзисторах. Резистивная сетка в этой схеме питает-

ся не от источника тока, а непосредственно от источника опорного напря-

жения Uo и вырабатывает двоично-взвешенные токи, поступающие на

МОП-переключатели S] * S

. С выводов ЦАП получаем два тока I] и 1

Ток

(

изменяется пропорционально управляющему коду N. Ток

— до-

полняющий и определяется соотношением I

- Ii, где

— максима-

льное значение тока Ij. У разных экземпляров этот ток лежит в пределах

0,5-;-2мА (номинальное значение 1о= 1мА).

Выходное напряжение ЦАП и

вых

снимается с выхода дополнительно-

го усилителя

А1

и определяется равенством U

BMX

» -UoN/N

max

. Поскольку

Uo может принимать как положительные, так и отрицательные значения,

то приведенная схема осуществляет двухквадрантное умножение Uo на

N. Для 4- квадрантного умножения ЦАП дополняется еще одним усили-

телем А2 и резисторами Ri * R3 (Rj = R

= 2R

). Напряжение на выходе

усилителя А2 можно определить как

Bblx2

= -U

bux1

R3/R

U0R3/R1

= 2U

(N - N

max

/2)/N

max

Если один из сомножителей U

—

Uo, а второй U

представлен сме-

щенным двоичным кодом N = a U

max

+ N

max

/2, где а — постоянный ко-

эффициент, то результат четырехквадрантного перемножения равен

выХ

2а U

ЦАП типа

К572ПА1

может управляться кодом с выводов дискретных

интегральных схем типов КМОП и ТТЛ. В последнем случае выходные

уровни следует поднять путем подключения к выходам этих микросхем

сопротивлений 2—10 кОм, которые своим вторым выводом подключают-

ся к источнику питания + 5 В. Можно произвести непосредственное со-

362

К555ИР23

К572ПА1

Рис. 9.105. Практическая схема ЦАП-кардирмонитора

гласование ЦАП с ТТЛ-схемами, уменьшив напряжение питания ЦАП до

5 В, но при этом возрастают погрешности преобразования.

В [17] приведена практическая схема ЦАП с фильтром низких частот

для сглаживания ступенчатости в выходном сигнале, применяемая в кар-

диомониторах(рис. 9.105). В этой схеме регистр

РГ

служит для промежу-

точного хранения цифровых данных. Схема работает с частотой выборки

250 Гц, имеет разрядность 8 и полосу пропускания

0,1

* 30 Гц при нерав-

номерности АХЧ ± 10%.

Умножающие ЦАП удобно использовать для построения усилителей

с управляемым коэффициентом усиления (например, автоматизирован-

ное изменение масштабов преобразования аналоговых сигналов под

управлением ЭВМ или специализированных микропроцессоров). Дейст-

вительно, если в схеме рис. 9.104 U

рассматривать как входное напряже-

ние, U

Bb[X

| как выходное напряжение усилителя, то коэффициент усиле-

ния этого усилителя

определяется по фор-

муле К

= -N/N

max

,TO

есть изменяется прямо

пропорционально ве-

личине Uo.

На основе умно-

жающего ЦАП может

быть построен так же

и неинвертирующий

усилитель с управляе-

мым коэффициентом

усиления. На рис.

9.106, а условно пока-

зана такая схема на

основе ЦАП К572ПА1,

и с. 9.106. Структура неинвертирующего усилителя (а)

в которой приведены

делителя (б)

363

U.,

Roc

liL

и.

б)

схематично управляемые сопротивления от

KOflaN и

одно постоянное со-

противление обратной связи [16].

В данном случае использовано обратное включение ЦАП: опорное

напряжение Uo подключено к выводу 1, соответствующему выходному

току

(в таком включении это входной

ток),

а выходное напряжение сни-

мается с вывода 15, на который подается обычно опорное напряжение.

Такое включение сетки R—2R обеспечивает напряжение на 15-м выводе,

пропорциональное управляющему коду N, причем при таком включении

пропорциональная зависимость сохраняется при любом постоянном со-

противлении нагрузки. Однако токовые МОП-ключи не рассчитаны на

переключение больших напряжений, поэтому рекомендуется выполнять

соотношение -IB < U

< ГВ.

Если нужно получить знакопеременное выходное напряжение для

смещенного кода при постоянном Uo, в схему вводится дополнительный

резистор Rj. В результате справедливо выражение

и,

ых

= и

. ~

max

В частности, если принять Ri = R, R

=1,25R, R

= 5R, то

U,„

= 10U

(N - N

max

/2)/N

max

Умножающий ЦАП может быть использован для реализации опера-

ции деления. На

рис.

9.106, б показана схема деления на ЦАП К572ПА1,

для чего ЦАП включен в цепь обратной связи усилителя.

Для этой схемы и

вых

-U

max

/N, причем следует иметь в виду, что

относительная погрешность этой схемы возрастает при малых значени-

ях N.

Глава 10

УСТРОЙСТВА ОБРАБОТКИ

ДИАГНОСТИЧЕСКОЙ ИНФОРМАЦИИ

10.1. МЕТОДЫ И АЛГОРИТМЫ ОБРАБОТКИ

ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ СИГНАЛОВ

В настоящее время известно достаточно большое количество методов

и алгоритмов обработки электрофизиологических сигналов, которые в

основном можно разбить на три большие группы.

1. Первая группа включает методы и алгоритмы, которые основаны

на анализе структуры исследуемых сигналов (длительность и амплитуда

волн и их различных участков, асимметрия, площадь, «махристость» и

«остроконечность» волн, частота пересечения волнами некоторых фик-

сированных уровней сигналов, в частности так называемой нулевой ли-

нии (изолинии), частота следования волн, исчисляемая по фиксации вре-

мен появления минимумов или максимумов волн и т.д.)

Разработаны методы и алгоритмы, позволяющие выделить информа-

тивные признаки, которые характеризуют различные структурные осо-

бенности временных составляющих исследуемых сигналов [17, 52, 53,

54]. Процесс выделения показателей, характеризующих структуру волн

сигналов, основывается на прямых измерениях временных и амплитуд-

ных характеристик характерных точек сигналов или

их

производных (ми-

нимумов, максимумов, точек перегибов, пересечений заданных ампли-

тудных уровней и т. д.) с возможным вычислением простейших расчет-

ных соотношений для получения производных параметров. С целью по-

вышения надежности измерений используют предварительную фильт-

рацию и усреднение исследуемых характеристик по нескольким волнам.

Иногда вместе с фильтрацией используют специальные приемы выделе-

ния и удаления артефактов, например путем пропускания исследуемого

сигнала через дискриминатор уровней.

Наибольшее распространение среди этих методов получил метод пе-

риодометрического анализа и некоторые его разновидности [55], в кото-

рых получение признаков для классификации основывается на фиксации

365

точек пересечения исследуемой кривой и ее производных с изолинией и

вычислениях средних значений и дисперсии значений временных отсче-

тов. Разработчик метода периодометрического анализа Берг утверждал

[52], что анализ периодов дает почти такую же информацию, что и час-

тотный анализ сигналов. Известны работы, в которых описаны практиче-

ские задачи классификации с использованием признаков, выделенных на

основе периодометрического анализа [53].

К достоинствам периодометрического метода, безусловно, следует

отнести простоту

низкую стоимость реализации, что позволяет разраба-

тывать различные технические средства и специальные вычислительные

устройства на основе простых операционных автоматов и микропроцес-

соров [53], которые в настоящее время находят широкое применение в

медицинской практике. Однако такой анализ обладает и рядом потенциа-

льных недостатков:

— частоты пересечения нулевого уровня для сигналов разного типа

могут оказаться одинаковыми;

— регистрируются лишь периодометрические свойства сигнала, тог-

да, как известно, что в ряде случаев информативными являются ампли-

тудные и планометрические характеристики, показатели асимметрии и

ряд других;

— колебания выше и ниже изолинии не обнаруживаются, пока не

определены частоты пересечения изолинии одной или несколькими про-

изводными;

— существенную погрешность

результате измерений вносит дрейф

изолинии;

— частоты пересечения для первой и второй производной могут

быть сильно зашумлены;

:— не обеспечивается выделение различных временных составляю-

щих и параметров переходных процессов.

Перечисленные недостатки объясняют тот факт, что при огромном

количестве исследований, выполненных в направлении использования

периодометрического анализа, в большом числе случаев получаемые ре-

зультаты нельзя признать удовлетворительными [53].

В качестве информативных признаков, характеризующих сигналы

более сложной статистической природы (типа электроэнцефалограмм,

электромиограмм, кожно-гальванических реакций и др.),используют те-

кущее значение модуля амплитуды сигналов, дисперсию среднего значе-

ния модуля, коэффициент асимметрии волны, коэффициент плосковер-

шинности волны, коэффициент «махристости», параметр формы волны,

отображение структурных свойств сигнала на фазовой плоскости и т. п.

Сложность функционирования биологических систем и большое ко-

личество информации, содержащейся в электрофизиологических сигна-

366

лах (ЭФС), не позволяет однозначно связывать значения отдельных пара-

метров сигналов с диагностическими врачебными заключениями. Поэто-

му следующим шагом в обработке ЭФС является поиск комплексных по-

казателей, зависящих от ряда измеряемых элементарных признаков, или

симптомокомплексов — комбинаций признаков (векторов признаков),

которые позволили бы повысить достоверность получаемых результатов.

При этом одним из самых популярных приемов стал подход, основанный

на применении методов теории распознавания образов, когда на этапе

обучения из совокупности признаков формируется множество данных в

виде специальных таблиц с указанием того, к какому диагностируемому

классу относится тот или иной набор параметров. Далее, с помощью спе-

циальных математических приемов находится решающее правило, по-

зволяющее отличать элементы таблиц различных классов [59]. На этапе

классификации решающие правила соотносят вектор признаков к одному

из классов, выделенных на этапе обучения.

Следует, однако, отметить, что успех решения задачи классификации

при таком подходе сильно зависит от того, удается ли найти такие наборы

информативных признаков, извлекаемых из ФС, которые позволяют

строить достаточно надежные решающие правила. Например, практика

использования такого подхода для сигналов со сложной статистической

природой (типа ЭЭГ, ЭМГ и др.) показала, что получить удовлетворите-

льные результаты удалось для весьма узкого класса задач. Например,

удается решать частную задачу определения стратегии лечения больных

эпилепсией на ранних стадиях возникновения болезни, но плохо диагнос-

тируются опухолевые процессы, различные типы психических рас-

стройств, тонких изменений в функциональном состоянии человека и

т. д. [53, 54, 57]. Связано это в первую очередь с тем, что, например, для

такого сигнала.как

ЭЭГ,

нет достаточно определенной информации как о

составе, так и о значимости признаков в записи ЭЭГ, нет унифицирован-

ного подхода к структуре и оценке сочетаний этих признаков.

2. Второй подход основывается на использовании различных матема-

тических моделей, позволяющих с достаточной точностью аппроксими-

ровать и (или) моделировать исследуемые процессы.

Среди методов аппроксимации известны такие, которые используют

сплайн-аппроксимацию, аппроксимацию полиномиальными, тригоно-

метрическими и экспоненциальными моделями. Параметры моделей мо-

гут быть определены, например, методом сингулярного анализа [53], ме-

тодом автокорреляционного

взаимно корреляционного анализа [53].

• Достаточно широкое распространение получили методы спектраль-

ного анализа, простейший из которых позволяет выделять различные час-

тотные составляющие исследуемых сигналов путем их пропускания че-

рез систему полосовых фильтров с известной полосой пропускания. Ши-

367

рокое распространение среди этих методов анализа ЭФС получили раз-

личные варианты классического спектрального анализа, основанные на

преобразованиях Фурье, Уолша, Хартли

и др.

В этом направлении для не-

которых частных задач получены хорошие результаты [53]. Однако ис-

следователи, активно использующие методы спектрального анализа для

обработки сложных сигналов, отмечают, что надежные результаты уда-

ется получить для весьма ограниченного круга задач. Такие ограничения

принято связывать со сложной, нестационарной природой исследуемых

процессов с недостаточно изученными типами нестационарностей, а так-

же с тем, что в медицинских приложениях спектр мощности редко слу-

жит конечным результатом, поскольку пользователя обычно интересуют

другие параметры, характеризующие в основном особенности наблюдае-

мых полуволн исследуемых сигналов. Хотя в настоящее время известны

подходы к обработке случайных нестационарных процессов, включая

применение методов спектрального анализа, но применительно к выделе-

нию информативных признаков

из

сигнала типа электроэнцефалограмма,

электромиограмма, они разработаны слабо.

С точки зрения вычислительных процедур, выделение информатив-

ных признаков методами спектрального анализа (за исключением приме-

нения полосовых фильтров для выделения различных частотных состав-

ляющих) представляется достаточно трудоемкой задачей. Поэтому для

практической реализации требуется либо использование специализиро-

ванных вычислительных средств, либо достаточно мощных микроЭВМ

или ЭВМ общего назначения, возможно,со специализированными сигна-

льными процессорами, например, серии КР 1815.

Для электрофизиологических сигналов, обладающих значительной

нестационарностью (например, при анализе спайков или «острых» волн в

сигналах), элементы нестационарности иногда легко обнаружить «на

глаз». Например, отчетливо видимый комплекс пик-волна при кратковре-

менном эпилептическом припадке имеет четко выраженную форму. Ана-

логичная ситуация возникает при выявлении вызванных потенциалов как

реакции на внешнее воздействие. Однако зачастую при преобладающем

фоновом шуме, то есть низком отношении с/ш, нестационарная актив-

ность трудно различима.

Непараметрические методы обнаружения нестационарностей обычно

основываются на непосредственном вычислении по записи ЭЭГ-сигнала

таких величин, как производные, длительности, амплитуды. Для обнару-

жения нестационарных компонент используются также некоторые мате-

матические функции этих величин.

Известные методы обработки нестационарных сигналов основаны на

применении согласованных фильтров. В этом случае должна быть изве-

368

стна форма волны, что является ограничивающим фактором, поскольку

формы волн могут значительно отличаться у разных людей и даже у од-

ного и того же человека. Заранее форму волны из всего встречающегося

разнообразия сигналов предсказать очень трудно.

3. Третья группа методов связана с оценкой степени «похожести»

(синхронности) протекания электрофизиологических процессов в разных

отведениях, различных участках одного

и того же

процесса

или

на разных

участках тела. Для этих целей нашли применение методы корреляцион-

ного анализа и различные меры близости изучаемых процессов [53]. В

ряде работ отмечается, что использование методов корреляционного ана-

лиза при решении задач обработки электрофизиологических сигналов за-

трудняется тем, что надежные результаты получаются в основном в слу-

чае исследования стационарных процессов. Вид корреляционных функ-

ций по своей сложности зачастую достигает сложности исследуемого

сигнала. При решении практических задач часто возникает необходи-

мость выяснения вопроса о том, за счет каких свойств или параметров

сигнала нарушается корреляционная связь. Непосредственный анализ,

корреляционной функции в общем случае ответа на причину рассогласо-

вания сигналов не дает.

В [56] рассмотрен структурный подход к исследованию степени син-

хронности протекания пар физиологических сигналов, позволяющий из-

мерять синхронность по амплитуде и направлению с учетом параметров,

которые характеризуют сдвиг фаз и амплитудную разность.

При всем разнообразии методов и алгоритмов автоматизированной

обработки электрофизиологических сигналов

целом

ряде

задач они зна-

чительно уступают по своей диагностической ценности заключениям,

выдаваемым опытными специалистами-электрофизиологами. Поэтому в

некоторых современных системах из электрофизиологических сигналов

выделяется та же информация, которую используют в своей практиче-

ской работе врачи-электрофизиологи, и затем реализуются соответству-

ющие решающие правила, моделирующие логику врачебного принятия

решений. В основном это правила продукционного типа, реализуемые в

соответствии с четкой и нечеткой логикой.

Рассмотренный в этом разделе далеко не полный перечень методов'

обработки электрофизиологических сигналов позволяет сделать вывод о

том, что для своей реализации они требуют весьма широкой номенклату-

ры технических средств различных типов и назначений, от простейших

электронных схем до сложных вычислительных комплексов и эксперт-

ных систем.

369

10.2. УСТРОЙСТВА ВЫЧИСЛЕНИЯ

ФОТОМЕТРИЧЕСКИХ ПАРАМЕТРОВ

Анализ технических характеристик образцов отечественных и зару-

бежных фотометрических медицинских приборов показывает, что по

виду измеряемого параметра можно выделить несколько типов устройств

первичной обработки сигналов ОЭИП. Они предназначены для измере-

ния следующих фотометрических параметров:

— коэффициентов пропускания, поглощения, отражения и других,

которые определяются через отношение сигналов ФПУ h = U1/U2;

— оптической плотности D = lg(U2/Ui) = lg(l/h);

— коэффициентов, характеризующих поглощающие свойства иссле-

дуемого образца через отношение сигналов, которые измерены в двух

спектральных областях излучения Xj и Х

Ь(Я.)

= U(Xi)/U(X

);

— медицинских показателей (например, характеризующих концент-

рацию, состав или тип вещества, содержащегося в образце), определяе-

мых через отношение двух или более сигналов.

Для разных фотометров различен и диапазон изменения этих пара-

метров, а также метрологические требования. Так, например, для коэф-

фициента пропускания т (см. табл. 10.1) максимальный диапазон измене-

ния соответствует диапазону изменения h = 0

-s-1,0.

Однако для ряда при-

боров диапазон изменения ограничивается величинами h = 0,2

-s-

0,6 или

h = 0,6 +

1,0.

Диапазон изменения оптической плотности D чаще всего ра-

вен 0 + 2, что соответствует изменению отношения сигналов h от 0 до

100. Аналогичная ситуация характерна и для других методов фотометри-

ческих исследований, вариантов фотометра и фотометрических парамет-

ров.

Для большинства фотометров задается абсолютная точность измере-

ний, при задании относительной погрешности оговаривается значение

измеряемого параметра, для которого обеспечивается эта погрешность.

Для медицинских фотометров обычно "относительная погрешность со-

ставляет

0,5 -г-

2,5 % при максимальном значении измеряемого параметра.

Однако в медико-биологической практике известны фотометрические за-

дачи, для решения которых требуется обеспечение предельных по точно-

сти, помехоустойчивости и чувствительности измерений.

Важной характеристикой устройства первичной обработки является

порядок поступления сигналов ОЭИП. Можно выделить одноканальные

устройства первичной обработки сигналов ОЭИП—устройства последо-

вательного действия, предназначенные для обработки последовательно

поступающих сигналов ОЭИП, и двухканальные — устройства паралле-

370

льного действия, позволяющие и,(|)_^7Т47иГ

обрабатывать сигналы, которые —' —

поступают на устройство первич- у ^

'ной обработки одновременно.

В общем случае устройства Рис. 10.1. Типовая структура измерителя

первичной обработки в фотомет- отношений сигналов

pax разных классов представляют

собой измерители отношения (ИО) сигналов, построенные на базе дели-

тельных схем и предназначенные для автоматического определения от-

ношения двух величин (представляемых в виде тока, напряжения, часто-

ты или кода) по выходному напряжению, коду, а

простейшем случае —

по показанию стрелочного или цифрового индикатора Как правило, ИО

(рис. 10.1) состоит из делительной схемы ДС, на которую после предва-

рительного усиления усилителями Yi и Y

поступают сигналы Ui и U

ОЭИП. Пределы измерения могут устанавливаться заранее или выбира-

ться с помощью переключателя пределов (ПП). Выходной сигнал ДС по-

сле прохождения через дополнительный усилитель

ДУ

фиксируется в ин-

дикаторном устройстве (ИУ), преобразующем выходной сигнал делите-

льной схемы в необходимый вид для дальнейшей обработки или индика-

ции.

Измерители отношения h достаточно полно характеризуются следу-

ющими показателями:

— относительной статической погрешностью 5

СТ

, определяемой в

установившемся режиме и характеризующей отличие измеренного зна-

чения отношения

от истинного

его

значения h

СТ

= (h„ - h

)/h

;

— динамическим диапазоном в децибелах, который определяется

отношением максимального значения сигнала делителя U2 к минималь-

ному, в пределах которого статическая погрешность деления не превы-

шает заданной величины — D = 201g(U2max - U

);

— диапазоном измеряемых отношений — Ьть h

max

;

— частотным диапазоном;

— быстродействием каналов — временами нарастания сигнала по

каналам делимого

делителя или общим временем установления резуль-

тата т

от

;

чувствительностью ВХОДОВ Uimin и U2min-

Входные цепи реальных устройств первичной обработки сигналов

ОЭИП могут незначительно отличаться от схемы, приведенной на

рис. 10.1, например, за счет включения схем суммирования — вычитания

сигналов при измерении фотометрических параметров, определяемых

через дробно-линейные функции сигналов ОЭИП. Возможно непосред-

ственное получение величины отношения в линейном масштабе или

' 371

определение медицинского показателя при известной функциональной

связи последнего с отношением входных величин. В последнем случае

выход ДС подключается к функциональному преобразователю отноше-

ния величин (ФП).

Приведенные выше рассуждения позволяют высказать предположе-

ние о возможности стандартизации устройств первичной обработки ме-

дицинских фотометров с учетом решаемых ими задач и разработке уни-

фицированной базовой схемы измерения отношения, пригодной для мно-

гих практических задач.

В [27] предложен ряд фотометрических приборов — ряд ФМП — с

типовыми по параметрам измерительными схемами. Каждая схема ряда

должна удовлетворять требованиям определенной группы приборов, раз-

личных

по

назначению, но близких по техническим характеристикам. Та-

кой ряд содержит всего восемь измерительных

схем.

Особенностью ряда

ФМП является включение в него схем, позволяющих вычислять парамет-

ры типа

= U

/( Ui + U

) и К = ( U

- U

)/(Ui + U

). Эти параметры, как

показывает теоретический анализ, могут заменить показатели типа к,

особенно при к> 1, обеспечивая при этом лучшие метрологические ха-

рактеристики фотометрического прибора в целом.

Таблица 10.1

Ряд измерительных схем

Измеряемый

фотометрический параметр

Диапазон изменения

параметра

0 — 1

0,2 —

0,6

0,6 —

1,0

0 — 2

0 —

100

0 —

-1 —

Достаточно простые и быстродействующие устройства первичной

обработки сигналов ОЭИП можно построить на базе схем измерения от-

ношений открытого типа, в частности с использованием метода анало-

го-временного преобразования. Этот метод позволяет для каждого типа

фотометра предложить базовую схему, характерной особенностью кото-

рой является возможность управления диапазоном изменения выходного

параметра

путем

изменения номиналов нескольких элементов электриче-

372

ской принципиальной схемы. Кроме ^

того, при незначительной модифи-

кации структуры базовой схемы она

может быть приспособлена для из-

мерения любого параметра из табл. Рис. 10.2. Структура базового варианта

10.1. устройства первичной обработки для

В качестве примера рассмотрим фотометров

структурную схему базового вари-

анта устройства первичной обработки (рис. 10.2) для наиболее часто

встречающегося фотометра с временным разделением двух потоков из-

лучения, предназначенного для измерения параметра h.

На вход устройства последовательно во времени поступают импуль-

сы, амплитуда которых равна Ui (числитель)

и U

(знаменатель). С прихо-

дом импульса числителя схема управления (СУ) открывает ключ К|.и в

устройство выборки-хранения (УВХ) записывается значение амплитуды

импульса

U|.

После окончания импульса числителя схема управления за-

крывает ключ К). В момент прихода импульса знаменателя открывается

ключ К

, через который этот импульс подается на интегратор (Инт). Вы-

ходной сигнал выборки-хранения поступает на устройство сравнения

(УС), на другой вход которого подается напряжение с интегратора и

ииг

Момент равенства

и и

инт

фиксируется в устройстве сравнения. Проме-

жуток времени t

с момента начала интегрирования до момента равенства

напряжений пропорционален измеряемому отношению h = U

. После

окончания импульса знаменателя закрываются ключи, при этом очищает-

ся устройство выборки-хранения и происходит установка начального

уровня интегратора—схема готова

следующему циклу измерений. Для

получения цифрового или кодового эквивалента отношения временной

интервал t

заполняется импульсами опорной частоты (Г), которые про-

ходят через схему пропускания (СП)

подсчитываются в блоке регистра-

ции результата (БРР).

Основными источниками погрешности измерения отношения в этой

схеме являются погрешности устройства выборки-хранения и интеграто-

ра, наличие порога срабатывания схемы сравнения, а также нелинейность

начального участка интегратора. Как показал анализ

[б],

передаточная ха-

рактеристика и интегральная систематическая погрешность устройства

определяется в соответствии с выражениями:

, «.Т. +«.Т, -t.t, «.T»-tS-t.t,

ГТГ ' *->—Г7гГ—

(101)

хр и • хр

373

где t

— реальная длительность импульса; t„ = ah — истинная длитель-

ность, пропорциональная измеряемому параметру h; a — масштабный

коэффициент; Т

хр

— постоянная времени схемы выборки-хранения;

= aAU/U

;

— абсолютная погрешность схемы сравнения; U

— амп-

литуда сигнала знаменателя; t

— временной интервал между импульса-

ми числителя и знаменателя; cp(t„) — интегральная систематическая по-

грешность.

Анализ выражения для абсолютной погрешности показывает, что

<р

= 0 при

t„ =0,5(^+41^-1,),

а при t„ = 0

<р

to-

Рассмотрим случай, когда t

—>

0. Введем обозначения t„/t„o = х;

o =

1/d;

tp/t„

= у; (p/t„

= Ду; t„

= ^t

. Тогда выражения (10.1) пре-

образуются к виду:

у = (х + d)/(xd + 1); Ду =

- x

)d/(xd + 1). (Ю.2)

На рис. 10.3 приведено семейство зависимостей Ду = f(x) для разных

значений а при

> 0. Полученные соотношения связывают основные па-

раметры рассмотренной базовой схемы ряда МФП с величиной допусти-

мой абсолютной погрешности Ду = Д

доп

. Так при х = 0 Ду = d, откуда

Ддоп*

Задаваясь величиной d, можно определить:

Xmax

= 0,5(Vd

+8+d)

и максимальное значение отношения амплитуд входных сигналов при

= const:

hmax = (Ui/U

)

max

= x

max

t„o/d . (10.3)

При t

значение h

max

уменьша-

ется примерно в [1 +(t

/t„)] раз.

Полученные соотношения спра-

ведливы для всех базовых схем, в ко-

торых использован метод анало-

го-временного преобразования, в

том числе и таких, которые предназ-

начены для измерения параметров

г и

374

AY*10-3

Рис. 10.3. Семейство зависимостей

AY = f(x) для различных значений d

при to > 0

Рис. 10.4. Устройство первичной

обработки с компенсацией погрешности

К. В последнем случае схема до-

полняется сумматорами и инверто-

рами сигналов.

Для компенсации погрешно-

стей измерения фотометрических

параметров можно использовать

известные в схемотехнике приемы.

Так, на рис. 10.4 приведена схема,

в которой вводится второе устрой-

ство сравнения УС

, а в качестве опорного напряжения используется

часть напряжения делимого или делителя. В схеме используется рези-

стивный делитель R| — R

и переключатель (Пр), который соединяет

один из входных сигналов с соответствующим устройством сравнения.

Например, если к делителю подключен сигнал U

то на вход УС| посту-

пает в качестве опорного сигнал UOI = UJR

/(RI + R

). УС| срабатывает в

момент времени T| = U

IT/U

= UJR

T/[U

(RI + R

)]. Для устройства УС

опорным уровнем является сигнал U|, поэтому момент срабатывания

= U|T/U

. Импульсы с УС1 и УС

управляют триггером (Тр), длитель-

ность импульса с которого tr

= t

- ti = kUj/U

= kh, то есть пропорцио-

нальна параметру h и не зависит от нелинейности интегратора.

Структура устройства первичной обработки фотометрических сигна-

лов повышенной точности приведена на

рис.

10.5. В этом варианте испо-

льзуется интегратор (Инт) со сбросом, управляемый от генератора тактов

(ГТ). Ко входу интегратора подключается сигнал знаменателя U

, а его

выходной сигнал поступает на два устройства сравнения УС] и УС

. На

второй вход УС] поступает сигнал с преобразователя опорного уровня

(ПОУ), а на второй вход УС

—сигнал с суммирующего устройства (СУ).

В суммирующем устройстве осуществляется сложение сигнала числите-

ля с некоторым опорным уровнем Uo, поступающим от источника опор-

ного напряжения (ИОН). Выходными импульсами с УС| и УС

, которые

появляются в моменты времени

ti и t

управляется триггер

(Тр).

Длитель-

ность выходного импульса:

= t

-1, - (k

U, +

IQUO

+ Дисг -

Ди

+ U, - k

)/(k,U

), (10.4)

где k| — величина, обратная постоянной времени интегратора; к

— ко-

эффициент преобразования ПОУ (k

1); кз

1с»

— весовые коэффициен-

ты суммирующего устройства; AU

ДИсг—пороги срабатывания соот-

ветствующих устройств сравнения; U^, — напряжение смещения нуля

суммирующего устройства.

Если выбрать k

(lc»Uo

+ U

- U

i + U^/Uo, то длительность импу-

льса, формируемого триггером, будет пропорциональна отношению сиг-

375

Сч1

КК ЬуЧечГ

->1 Сч2 W

Рис. 10.5. Устройство первичной

обработки повышенной точности

Рис. 10,6. Базовый вариант цифрового

устройства первичной обработки

налов, то есть t

= k

Ui/(kiU

). В этом устройстве повышение точности

достигается за счет уменьшения погрешностей, вызываемых неравенст-

вом порогов срабатывания устройств сравнения и смещением нуля сум-

мирующего устройства. Выполнение условия k

обеспечивается при

использовании в качестве преобразователя ПОУ резисторного делителя

напряжения. С другими вариантами аналоговых базовых схем устройств

первичной обработки сигналов можно ознакомиться в [6].

Аналоговая базовая схема не является единственно возможной. Ре-

жим импульсного питания источника излучения позволил предложить

оптико-электрические измерительные преобразователи, в которых сигна-

лы представлены последовательностью импульсов Ni и N

. Для таких

ОЭИП возможен другой вариант базовой схемы, реализующий типовые

операции над импульсными сигналами. Один из возможных вариантов

цифрового устройства первичной обработки приведен на рис. 10.6.

Пусть на вход схемы последовательно поступают две серии импуль-

сов- N, и N

, пропорциональные сигналам U, и U

. При подаче серии N

переключатель (П) подключает вход устройства первичной обработки к

делителю частоты (ДЧ). Коэффициент деления к

определяет точность

деления (количество разрядов в цифровом эквиваленте). Импульсы с вы-

хода ДЧ поступают на счетчик Счь в котором за время передачи серии N

накопится число импульсов

= N

. При подаче серии N

(

переключа-

тель соединяет вход схемы со счетчиком Сч

и начинается счет импуль-

сов. Разрядные выходы Сч

связаны с компаратором кода

(КК),

на второй

группе входов которого находится код числа

Компаратор постоянно

сравнивает коды входных чисел; при совпадении кодов на выходе компа-

ратора появляется импульс единицы, который подается на счетчик Сч

на сброс счетчика

Сч

Счетчик Сч

обнуляется,

но,

так как серия Ni

не

за-

кончена, он продолжает счет этих импульсов при одновременном сравне-

нии результата счета

кодом

Это происходит

до

тех пор, пока на ин-

формационный вход счетчика Сч

поступает серия N,. При окончании

этой серии на счетчике Сч

накопится результат: n = E[N|/AN

], который

376

является цифровым эквивалентом отношения NI/N

. Емкость счетчиков

Сч| и Сч

определяет динамический диапазон работы схемы, то есть пре-

делы изменения сигнала U

. При изменении значения U

автоматически

изменяется число AN

(вес одного счетного импульса результата)

схема

адаптируется к этим изменениям. Данная схема может быть подключена

и к аналоговому ОЭИП, только в этом случае подключение осуществля-

ется через преобразователь «напряжение—частота импульсов».

Тот или иной фотометрический параметр не всегда является выход-

ным параметром прибора. Для физиологических исследований характер-

ной задачей является определение по значению параметра целого комп-

лекса диагностических показателей, таких, как насыщение крови кисло-

родом, количество и тип фермента, витамина

других биологических ве-

ществ и т. п. Вычисление таких медицинских показателей может быть

осуществлено непосредственно в фотометре при включении в структуру

устройств первичной обработки функциональных преобразователей (см.

рис. 10.1). Весьма эффективным также для преобразования фотометриче-

ских параметров или сигналов ФЭП в диагностические показатели пред-

ставляется использование средств микропроцессорной техники. В этом

случае программным путем удается осуществить необходимую функцио-

нальную зависимость между измеренными сигналами и конечным пока-

зателем. Методы разработки подобных преобразователей для фотометри-

ческих приборов не имеют особенностей по сравнению с другими облас-

тями применения микропроцессорных наборов.

10.3. СИНТЕЗ УСТРОЙСТВ ОБРАБОТКИ

БИОМЕДИЦИНСКОЙ ИНФОРМАЦИИ

Специфика проектирования устройств обработки электрофизиологи-

ческой информации определяется, прежде всего уникальными особенно-

стями биообъекта и обязательными требованиями обеспечения его безо-

пасности. В то же время при проектировании аппаратуры для обработки

электрофизиологической и фотометрической информации необходимо

удовлетворять ряд других требований — к реализуемым функциям, ре-

шаемым задачам, условиям функционирования и т. п., которые носят в

основном неформальный характер. Причем для реализации одних и тех

же функций могут быть выбраны различные способы получения инфор-

мации, различные алгоритмы обработки и различные структуры соответ-

ствующих устройств и систем. При выборе варианта конкретного техни-

ческого решения, после определения и уточнения перечня решаемых за-

дач и функций, а также после предварительной оценки сложности реали-

зуемых вычислительных и управляющих процедур рекомендуется

оценить возможность и сложность реализации при структурно-функцио-

377