Письменный Е.Н. Теплообмен и аэродинамика пакетов поперечно-оребренных труб

Подождите немного. Документ загружается.

ГЛАВА 1

В работах [35, 36] была предпринята попытка создать прибли-

женный метод расчета теплоотдачи одиночной трубы с поперечным

шайбовым оребрением, а также пакетов таких труб. При этом ис-

пользовалась модель обтекания ребристой трубы, построенная на

предполагаемой авторами аналогии с моделью омывания гладкого

цилиндра. Общность процессов в гладкотрубных и ребристых паке-

тах, по их мнению, подтверждается исследованиями [12, 38, 39], в

частности, данными о том, что числа Струхаля для следа за оребрен-

ным и гладким цилиндрами отличаются незначительно, как и струк-

туры кормовых циркуляционных зон. Основываясь на этом, авторы

сочли возможным применить для определения интенсивности теп-

лоотдачи на поверхности ребра распределение скоростей, имеющее

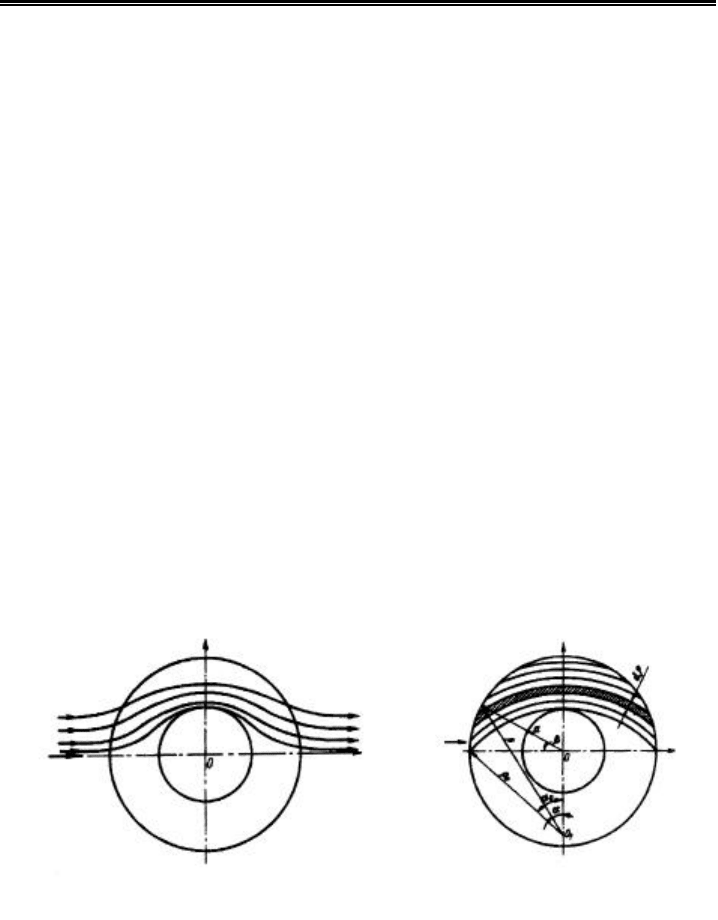
место при потенциальном обтекании гладкого цилиндра (рис.1.8).

Локальные и средние коэффициенты теплоотдачи в пределах эле-

ментарных полосок, на которые разбивалась поверхность ребра, рас-

считывались по формулам [40, 4I] для пластины при турбулентном

режиме течения. Несмотря на простоту принятой авторами [35, 36]

физической модели, метод расчета теплообмена получился крайне

громоздким. Точность же его, по нашим оценкам, оставляет желать

лучшего, что вполне объяснимо неадекватностью принятой модели

истинной картине процессов в поперечно-оребренных поверхностях.

Рис. 1.8. Схема обтекания ребристой трубы (а) и разбиение поверхности ребра на

элементарные полоски (б) в соответствии с моделью [35, 36]

В работе [37] модель обтекания ребристой трубы, исполь-

зуемая для расчета коэффициентов теплоотдачи по ее поверхности,

построена на результатах исследований в межреберном зазоре, ко-

торые выполнялись с помощью пневмометрических трубок в облас-

ти значений чисел Рейнольдса Re = 10

...10

. В соответствии с пред-

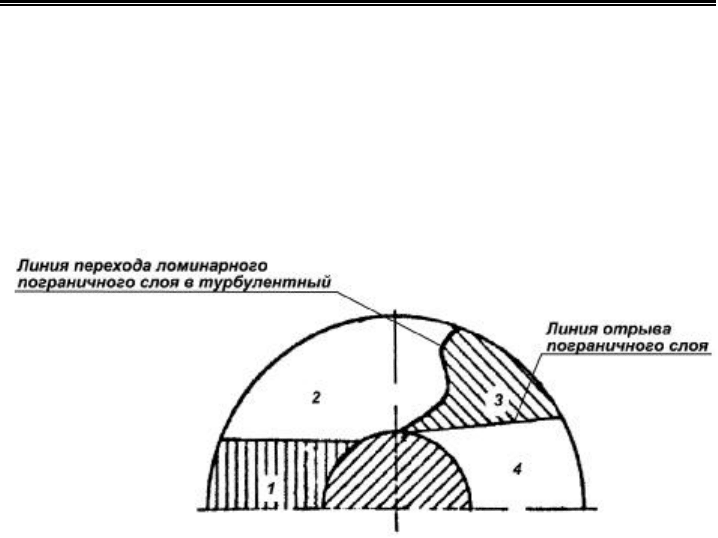
ложенной авторами схемой (рис.1.9) поверхность ребра можно

разделить на четыре участка:

- область неустойчивого диффузорного движения жидкости,

лежащую в лобовой части ребра (I);

- примыкающую к ней область квазипотенциального течения

(2) в которой, по мнению авторов, скорость можно определить по

Выводы 1.3

формулам потенциального обтекания цилиндра (принимается, что в

пределах перечисленных двух областей сохраняется ламинарный

режим движения в пограничном слое);

- расположенную за миделевым сечением область (3), в кото-

рой при сохранении квазипотенциального течения в ядре теплооб-

мен осуществляется через турбулентный пограничный слой;

- кормовую область отрывного течения.

Рис. 1.9. Схема характерных областей на поверхности ребра в соответствии с

моделью [37]

В качестве доказательства того, что в первой и второй областях

развивается ламинарный пограничный слой, в работе приводится

сопоставление опытных и рассчитанных с помощью уравнений по-

граничного слоя значений местного коэффициента сопротивления на

фиксированном радиусе ребра в интервале w = 0°...100°. Локальные

коэффициенты теплоотдачи на первых трех участках предлагается

рассчитывать методами теории пограничного слоя с учетом попра-

вок на трехмерность течения у поверхности ребра. Для четвертого

участка отмечается неясность характера движения жидкости и пред-

полагается оценивать только среднюю по участку интенсивность те-

плоотдачи на основе зависимости

Nu = 0,02 Re, (1.1)

полученной путем обработки соответствующих экспериментальных

данных из работы [2]. Следует обратить внимание на высокое значе-

ние показателя степени при числе Рейнольдса в уравнении (1.1) -

m = 1,0, характерное для областей течения с высоким уровнем воз-

мущенности потока. Таким образом в публикации [37] используется

уже более адаптированная, однако, все еще далекая от реальной мо-

дель процессов у поверхности ребристой трубы.

ГЛАВА 1

1.2. Среднеповерхностный теплообмен и аэродина-

мическое сопротивление пакетов труб с винтовым и

шайбовым оребрением

Большое число работ, посвященных изучению среднеповерх-

ностного теплообмена и аэродинамического сопротивления попе-

речно-омываемых пакетов труб с винтовым и шайбовым оребрени-

ем, свидетельствует о значительном интересе к результатам такого

рода исследований, обусловленном потребностями энергомашино-

строительной и других отраслей промышленности, а также о трудно-

стях, с которыми эти исследования связаны ввиду сложности про-

цессов в теплообменниках из поперечно-оребренных труб.

Подробные обзоры работ, выполненных в период 1945-1970 гг., со-

держатся в монографиях ЦКТИ [42] и ИФТПЭ АН Литвы [2]. В этой

связи представляется целесообразным ограничиться общей характе-

ристикой исследований отмеченного периода и подробнее остано-

виться на публикациях, появившихся после 1970 года.

Большинство работ раннего периода [18-20, 43-58] можно оха-

рактеризовать сходством подходов к решению поставленных задач и

относительной узостью интервалов геометрических и режимных ха-

рактеристик, при которых проводились исследования. Эксперимен-

тальные данные по теплообмену обрабатывались на основе приве-

денных коэффициентов теплоотдачи a

пр

и описывались для

отдельных пакетов или их небольших групп уравнениями подобия

вида

пp

= C

пp

(1.2)

Поиски возможностей обобщения данных в основном своди-

лись к подбору определяющего размера в числах Нуссельта и Рей-

нольдса, определяющей температуры и скорости, а также безразмер-

ных геометрических параметров, входящих в выражение для

коэффициента С

пр

. Показатель степени k при числе Re, как правило,

принимался постоянным. В качестве определяющего размера выби-

рался диаметр неcущей трубы d [18, 44, 48, 49, 52, 56, 57], наружный

диаметр оребрения D [20, 53], шаг ребер t [47], гидравлический диа-

метр [46], диаметр гладкой трубы с внешней поверхностью, равно-

великой поверхности оребренной трубы d

= d×ψ [5Ι], размер l¢ [54],

определяемый по соотношению

тррp

= (

Н /Н d + Н /Н H2z

)()

, (1.3)

и некоторые другие. Определяющей скоростью служила скорость

набегающего на пакет потока [20, 53] или скорость в сжатом попе-

речном сечении пакета [18, 43-49, 51, 52, 54-57]. Физические

Выводы 1.3

константы в числах Nu и Re определялись по средней температуре

потока в пакете [20, 43-47, 49, 51-57], по температуре стенки трубы

[48], а также по температуре, взятой как среднее значение между

температурой потока и стенки [18]. Эксперименты проводились как

методом полного, так и методом локального теплового моделирова-

ния*. Подходы, которыми пользовались авторы, ограничивали воз-

можности получения зависимостей, обобщающих эксперименталь-

ные данные в широком интервале геометрических и режимных

характеристик. В то же время следует выделить работы [44, 47], со-

держащие методические особенности, использование которых впо-

следствии позволило подойти к разработке обобщенного метода рас-

чета теплообмена пакетов оребренных труб. В работе [44] такой

особенностью явилось то, что авторы предложили учитывать в урав-

нениях подобия (1.2) зависимость величины показателя степени k

при числе Re от параметров оребрения. В работе [47] предложено

обобщать экспериментальные данные на основе конвективных, а не

приведенных коэффициентов теплоотдачи.

Экспериментальные исследования аэродинамического сопро-

тивления, проводившиеся, как правило, параллельно с исследова-

ниями теплообмена, в большинстве случаев ограничивались узкими

интервалами геометрических и режимных характеристик. Подход к

обобщению результатов экспериментов на основе зависимостей вида

Eu = C

×Re

- n

× z

(1.4)

характеризуется методами, аналогичными тем, что использовались

при обобщении данных по теплообмену. Единственным исследова-

нием, автор которого обратил внимание на зависимость показателя

степени n при числе Рейнольдса в формуле для определения величи-

ны сопротивления от геометрии пучка, является публикация [43],

выделяющаяся, кроме того, среди других исследований раннего пе-

риода наиболее широким интервалом варьирования параметров раз-

мещения труб.

Многие работы более позднего периода по методике и характе-

ру выполненных исследований мало отличаются от работ раннего

периода. В публикации [59] приводятся результаты исследований

теплоаэродинамических характеристик двух шахматных пакетов из

биметаллических труб с алюминиевыми ребрами и коэффициентом

оребрения, равным 15,23, в интервале Re = 5×10

...2,5×10

. Пакеты

имели шаговые характеристики

S/d = S/d = 1,04

¢ и

S/d = S/d = 1,14

¢ . В экспериментах использовался пароэлектриче-

ский калориметр, обеспечивающий, по мнению авторов, высокую

____________________

*) В публикациях, посвященных исследованиям теплообмена пучковых труб приня-

то называть экспериментальную методику, при которой обогреваются все трубы пучка ме-

тодом полного теплового моделирования; методику, при которой обогревается только труба

– калориметр называют методом локального теплового моделирования.

ГЛАВА 1

равномерность температуры внутренней поверхности трубы. Теплооб-

мен исследовался методом локального моделирования с обобщением

результатов формулой вида (1.2), в которую авторы ввели поправочный

коэффициент С

лок

для приведения опытных данных к условиям полного

теплового моделирования. Данные по сопротивлению для каждого па-

кета описаны формулой типа (1.4), где в качестве параметра фигуриру-

ет коэффициент оребрения. В такой же мере узкий характер имеют те-

плообменные исследования [60], выполненные с тремя шахматными

пакетами стальных труб, имеющими ψ = 3,55...5,25 и S

= 0,89...1,19

в условиях локального моделирования при значениях Re = 3,5·10

...

4,5·10

. Исследования [61] связаны с определением теплоаэродинами-

ческих характеристик одно- и двухрядных компоновок ребристых труб

в области чисел Рейнольдса Re

= 8·10

... 8·10

. Результаты приводятся

в графическом виде. В работе [62] исследовался теплообмен одиноч-

ных алюминиевых труб с винтовым накатанным оребрением в интер-

вале чисел Рейнольдса Re = 4·10

... 8·10

при относительно широком

варьировании параметров оребрения (ψ = 1,93...9,72). Авторы отмечают

снижение интенсивности теплоотдачи труб при увеличении высоты

ребер (шаг и толщина ребер, а также диаметр несущей трубы были по-

стоянными) и связывают это с увеличением глубины межреберной по-

лости h/u. Результаты экспериментов описываются формулами типа

(1.2), где в качестве параметров, определяющих коэффициент С

пр

, вве-

дены коэффициент оребрения ψ и величина h/u. В последующих рабо-

тах тех же авторов [21, 22, 63] методом полного теплового моделирова-

ния исследовался теплообмен шахматных пакетов медных,

алюминиевых и стальных труб с винтовым оребрением, а также их аэ-

родинамическое сопротивление. Основное внимание авторов было на-

правлено на изучение влияния на теплоаэродинамические характери-

стики пакетов геометрии ребристых труб, в связи с чем, в этих работах

довольно широко варьировались высота и шаг ребер (h = 3...10 мм;

t = 1,5...4,5 мм), а также диаметр несущей трубы (d = 6,2...25,4 мм).

Параметры размещения труб в пакете не варьировались и составляли

/D = 1,25 и S

/D = 1,08 (S

» 1,1). Результаты экспериментов

аппроксимировались зависимостями типа (1.2), (1.4) для каждого паке-

та отдельно. При этом показатели степени k и n при числах Рейнольдса

принимались постоянными, а значения коэффициентов С

пр

и С

дава-

лись в табличном виде. Авторы делают вывод, что для труб, характери-

зующихся значениями h/u £ 2 свойственна прямая пропорциональность

между ростом поверхности и съемом тепла с нее, а при h/u > 2 закон

пропорционального съема тепла нарушается, интенсивность теплооб-

мена уменьшается, что по их мнению связано с ухудшением гидродиа-

мических условий обтекания корневых частей ребер и трубы, несущей

оребрение.

В выполненной несколько ранее работе [64] исследовано влияние

теплопроводности металла ребристых труб на теплоотдачу. Для этого в

пакеты труб, изготовленные из углеродистой стали и имеющие

Выводы 1.3

/D = 1,04, S

/D = 0,91, ψ = 7,34…12,6, устанавливались стальные,

медные, и латунные калориметры. Были проведены также опыты с

пакетом из дюралевых труб. Результаты экспериментов, выполненных

методом полного теплового моделирования, позволили авторам сде-

лать вывод о том, что термическое сопротивление ребра не оказывает

решающего влияния на процесс теплоотдачи через ребристую по-

верхность, и что основным является термическое сопротивление теп-

лоотдачи к воздушному потоку, которое полностью зависит от гидро-

динамических условий их обтекания. Аналогичный вывод был ранее

сформулирован в монографии [44]. Полученные в этих исследованиях

данные позже были проанализированы теми же авторами с позиций

влияния глубины межреберной полости на теплообмен ребристых

труб [23]. Сделанные при этом выводы соответствуют изложенным

выше выводам работ [ 21, 22,63 ]. Предложены обобщающие выраже-

ния для двух областей изменения параметра h/t. Выражение для об-

ласти h/t > 1,8 помимо параметров ψ и l

, входящих также в выра-

жение для области h/t < 1,8, содержит комплекс h/t.

Работы [59, 65-70], в отличие от рассмотренных выше [21-

23,62-64], в большей мере направлены на исследование влияния ша-

говых характеристик шахматных пакетов оребренных труб на их те-

плообмен и аэродинамическое сопротивление. Авторы публикации

[65] методом локального теплового моделирования исследовали теп-

лообмен девяти пакетов алюминиевых труб с коэффициентом ореб-

рения ψ = 7,5 в интервале отношения шагов S

= 1,05...1,77 при

значениях чисел Рейнольдса Re = 2,2×10

...2,3×10

. Исследования по-

казали существенную зависимость интенсивности теплообмена от

компоновки пакета, что было учтено в обобщающей формуле типа

(1.2) введением параметра j

, в степени 0,4. В работах [67-70] было

выдвинуто и экспериментально обосновано предположение о зави-

симости показателя степени (ρ) при параметре размещения j

от

геометрии ребристых труб. Значения ρ определялись при различных

величинах коэффициента оребрения ψ, в результате чего было полу-

чено аппроксимационное соотношение вида

ρ = 0,53 - 0,019×ψ, (1.5)

применение которого рекомендуется в интервалах ψ = 5...22;

= 0,68...2,27 и Re = Ι,4·10

...Ι,5·10

. Еще более широким принят

интервал варьирования шаговых характеристик в работе [66]

= 0,6...5,3), в которой выполнены исследования теплообмена и

аэродинамического сопротивления 14 шахматных пакетов медных

труб с накатанным оребрением, имевших ψ = 4,22, в области чисел

Рейнольдса Re = 2×10

...3×10

. Теплообменные эксперименты прово-

дились методом полного теплового моделирования. Авторы обрати-

ли внимание на переменность величины показателя степени при

числе Re в формуле (1.2), использовавшейся для аппроксимации

ГЛАВА 1

опытных данных, однако приняли его в итоге постоянным (k = 0,73).

Следует заметить, что при последующем анализе данные экспери-

ментов по теплообмену оказались завышенными по сравнению с

наиболее надежными данными других исследований. Это обстоя-

тельство позволило предположить, что в теплообменных экспери-

ментах [66] допущены методические погрешности. Результаты ис-

следований аэродинамического сопротивления показали заметное

влияние на его величину шаговых характеристик пакетов.

Особенностью работы [71] является то, что исследования теп-

лообмена и сопротивления шахматного пакета оребренных труб с

ψ = 9,12 и S

= 1,16 выполнены в ней при очень низких числах

Рейнольдса Re = 5…121. Кроме того, в отличие от рассмотренных

выше работ, где в качестве определяющего принят один из простых

размеров оребренной трубы d или t, в [71] числа Nu и Re определя-

лись по величине гидравлического диаметра. Результаты экспери-

ментов обобщены формулами

Nu = 0,16 – 0,062Re

1/2

+ 0,11Re

1/3

; (1.6)

Eu =

(1 + 0,14Re

1/2

+ 0,06Re

2/3

). (1.7)

Необходимо отметить, что позиции авторов исследований по-

следнего периода в отношении выбора определяющей скорости и

температуры совпадают: скорость относится к наиболее узкому се-

чению пакета (поперечному или диагональному), а физические па-

раметры потока определяются по его средней температуре. В отно-

шении же выбора определяющего размера представляет интерес

анализ, выполненный в монографии [7]. Обработав опытные данные

для нескольких пакетов ребристых труб различной геометрии с ис-

пользованием практически всех известных из литературы видов оп-

ределяющих размеров и сопоставив результаты этой обработки, ав-

торы пришли к выводу, что ни один из предложенных в качестве

определяющего размеров не имеет преимуществ перед другими при

обобщении результатов экспериментов по среднеповерхностному

теплообмену формулами вида (1.2).

Обратимся далее к наиболее важным обобщающим исследовани-

ям, с которыми связаны основные этапы разработки инженерных мето-

дов расчета среднеповерхностного теплообмена и аэродинамического

сопротивления пакетов труб с винтовым и шайбовым оребрением.

Обширные исследования теплообмена и сопротивления шахмат-

ных пакетов труб с винтовым оребрением в потоке воздуха выполнены в

ИФТПЭ АН Литвы, результаты которых обобщены в монографии [2].

Эксперименты проведены с 21 пакетом труб, геометрические характери-

стики которых соответствуют интервалам ψ = 3,09...10,6 и S

1,3…2,83. Среднеповерхностный теплообмен исследовался методом ло-

кального моделирования. Обоснование возможности применения этого

Выводы 1.3

метода авторы в основном связывают с тем, что эксперименты проводи-

лись в области больших чисел Рейнольдса Re = 2×10

…1×10

, где разница

в результатах, полученных полным и локальным моделированием, суще-

ственно снижается. Высокие значения чисел Re достигались за счет по-

вышения давления в замкнутом аэродинамическом контуре эксперимен-

тальной установки до 2,5 МПа. В опытах определялись приведенные

коэффициенты теплоотдачи, которые впоследствии для обобщения ре-

зультатов теплообменных экспериментов пересчитывались на конвек-

тивные посредством определения эффективности ребра с учетом ее за-

висимости от неравномерности a-поля. Система пересчета была

существенно уточнена по сравнению c предложенной в [47], о чем под-

робней сказано в главе 4. Определяющим размером взят диаметр несу-

щей трубы d. Обобщение осуществлено для двух областей исследован-

ного интервала чисел Рейнольдса - 2×I0

< Re < 2×I0

и 2×I0

< Re < 1×10

на границе которых (при Re = 2×10

) зависимость lgNu = f(lgRe) испыты-

вает перелом. Для первой области рекомендуется соотношение

0,2

0,180,14

0,80,4

Sth

Nu = 0,05RePr

Sdd

æö

æöæö

ç÷ç÷

ç÷

èøèø

èø

(1.8)

для второй

0,2

0,180,14

0,950,4

Sth

Nu = 0,08RePr

Sdd

æö

æöæö

ç÷ç÷

ç÷

èøèø

èø

. (1.9)

Выполненное нами сопоставление формул (1.8), (1.9) с экспе-

риментальными зависимостями, взятыми из работ [51,72], показало

относительно хорошее их согласование только в области, близкой к

нижней границе исследованного интервала чисел Re. Результаты

опытов по исследованию аэродинамического сопротивления рас-

сматривались отдельно для области чисел Re со степенным законом

изменения сопротивления и автомодельной области, причем граница

этих областей не была постоянной и менялась в зависимости от гео-

метрии пакетов в пределах Re = 7·10

…2·10

. Уклон зависимостей

lgEu = f(lgRe) также оказался заметно не постоянным. Несмотря на

это, авторы сочли возможным обобщить экспериментальные дан-

ные формулой вида (1.4) с постоянным показателем степени при

числе Re, а границу двух характерных областей чисел Рейнольдса

фиксировать на значении Re = 1·10

. Предложенные обобщающие

соотношения имеют вид:

при 10

< Re <10

1,4

1,80,55-0,5

0,25

thSS

Eu = 6,5511Rez

dddd

æöæöæöæö

ç÷ç÷ç÷ç÷

èøèøèøèø

; (1.10)

ГЛАВА 1

при 10

< Re < 10

1,4

1,80,55-0,5

thSS

Eu = 0,3711z

dddd

æöæöæöæö

ç÷ç÷ç÷ç÷

èøèøèøèø

. (1.11)

Выполненное в монографии [2] сопоставление формул (1.10),

(1.11) с обобщающими соотношениями, полученными в ЦКТИ [73],

обнаружило заметные расхождения в величинах сопротивлений, рас-

считанных двумя способами, причем более высокие значения чисел

Eu дает расчет по формулам (1.10), (1.11). Авторы отмечают также,

что в пределах исследованных интервалов параметров размещения

труб теплоотдача пакетов изменялась незначительно, примерно на

20 %, в то время как сопротивление менялось почти на 60 %.

Дальнейшим развитием работы [2] являются исследования [25,

74], направленные на определение влияния физических свойств теп-

лоносителя, температурного фактора и геометрии оребрения на

среднеповерхностный теплообмен шахматных пакетов поперечно-

оребренных труб, а также на изучение закономерностей их гидрав-

лического сопротивления в условиях широкого изменения чисел

Прандтля 0,7 < Рг < 4,4×10

. Для проведения экспериментов в столь

широком диапазоне чисел Рr в работах использовались замкнутые

гидродинамические контуры, рабочими телами в которых служили

воздух, вода, трансформаторное и авиационное масла. Интервал чи-

сел Рейнольдса при этом составлял 5×10

< Re < 2,9×10

. Существен-

ным методическим недостатком, который не мог не сказаться на ре-

зультатах рассматриваемых исследований, было то, что большинство

экспериментальных трубных пакетов имело недопустимо малое с

позиций соответствия модели реальным условиям количество труб в

поперечном ряду (z

= 2). В работе [74] опыты выполнялись с пятью

пакетами труб, имеющими следующие характеристики: ψ =

1,43...5,13; S

/d = 1,13...1,66; S

/d = 1,06…1,53; S

= 1,1. Это одно

из немногих исследований, где в теплообменных экспериментах не-

посредственно определялись конвективные коэффициенты теплоот-

дачи, для чего авторами применен устанавливавшийся на трубе-

калори-метре узкий радиальный медный элемент с 3...6 термопара-

ми, предназначенный для измерения температур по высоте ребра.

Измерения всего поля температур осуществлялись вращением кало-

риметра вокруг продольной оси с интервалом 10°. Анализ результа-

тов экспериментов показал увеличение показателей степени при

числах Re в выражениях для конвективной теплоотдачи и сопротив-

ления с ростом высоты ребра. При этом имеет место также увеличе-

ние коэффициента сопротивления. Однако в предложенных автора-

ми обобщающих соотношениях отмеченные показатели степени

приняты постоянными:

Выводы 1.3

при 5×10

< Re < 2×10

0,25

0,2

0,180,14

0,650,36

SthPr

Nu = 0,192RePr

SddPr

æö

æöæö

ç÷ç÷

ç÷

èøèø

èø

; (1.12)

при 2×10

< Re < 8×10

0,25

0,2

0,180,14

0,720,36

SthPr

Nu = 0,097RePr

SddPr

æö

æöæö

ç÷ç÷

ç÷

èøèø

èø

; (1.13)

при 5×10

< Re < 10

0,550,5

0,50,3

Eu = 5,1Re

ψ .

æöæö

ç÷ç÷

èøèø

(1.14)

Итог выполненных в ИФТПЭ АН Литвы исследований тепло-

аэродинамических характеристик шахматных пакетов поперечно-

оребренных труб подведен в монографиях [17,75], где авторы в ре-

зультате анализа собственных и литературных данных предлагают

использовать для расчета среднеповерхностного теплообмена паке-

тов, имеющих s

= 1,1...4,0; s

= 1,03...2,5; t/d = 0,06...0,36;

h/d = 0,07...0,7I5 в интервале Re = 5·10

…2×10

зависимость (1.12), а в

интервале Re = 2×10

...2×10

- зависимость (1.8). Применительно к

области Re = 2×10

…1,4×10

авторы рекомендуют соотношение (1.9),

справедливое при s

= 2,2...4,2; s

= 1,27...2,2; t/d = 0,125...0,28;

h/d = 0,125...0,6. Для расчета аэродинамического сопротивления

шахматных пакетов в интервалах ψ = 1,9...16,0; s

= 1,6...4,13;

= 1,2...2,35; Re = 10

…1,4×10

в публикациях [17,25,75] прелагается

использовать формулы ВТИ (1.15), (1.16), полученные в работе [76].

В упомянутой работе ВТИ [76] предпринята попытка обобще-

ния опытных данных по аэродинамическому сопротивлению, взятых

из публикаций [2, 18, 19, 24, 43, 44, 46, 48, 54, 55, 57]. Необходи-

мость разработки новых расчетных соотношений базировалась на

выполненном авторами анализе наиболее известных методик расчета

аэродинамического сопротивления пакетов поперечно-оребренных

труб, из которого следует, что рассмотренные методики не охваты-

вают всех имеющихся в литературе экспериментальных данных и не

обеспечивают требуемой точности расчетов. Основной идеей

обобщения является использование в качестве параметра,

учитывающего геометрию ребристых труб, коэффициента оребрения