Пирс Б. Типы в языках программирования

Подождите немного. Документ загружается.

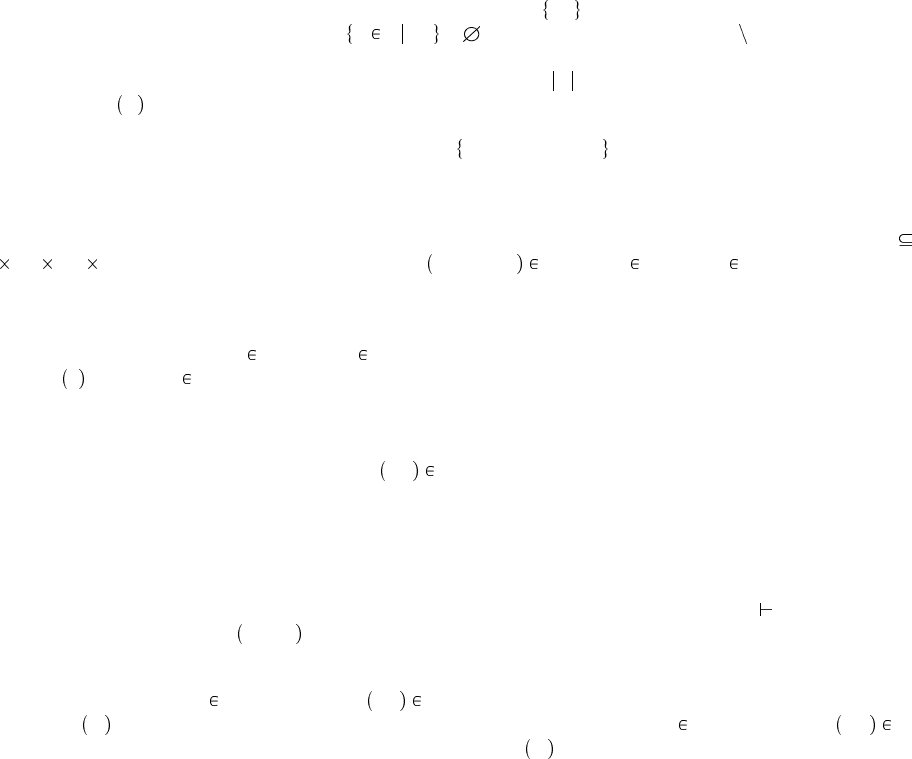
Глава 2

Математический аппарат

Прежде, чем начать, нам нужно договориться об используемых обозначениях и упомянуть несколько

базовых математических утверждений. Большинство читателей может бегло проглядеть эту главу и

затем возвращаться к ней по мере необходимости.

2.1. Множества, отношения и функции

Определение 2.1.1 Мы пользуемся стандартными обозначениями для множеств: фигурные скобки,

когда элементы множества перечисляются явным образом ( . . . ) или когда оно задается через «вы-

деление» на основе другого множества ( x S . . . ), для пустого множества, S T для теоретико-

множественной разности S и T (множество элементов S, не являющихся элементами T ). Мощ-

ность (количество элементов) множества S обозначается S . Множество всех подмножеств S

обозначается ℘ S .

Определение 2.1.2 Множество натуральных чисел 0, 1, 2, 3, 4, 5, . . . обозначается символом N. Мно-

жество называется счетным, если между его элементами и натуральными числами существует

взаимно-однозначное соответствие.

Определение 2.1.3 n-местное отношение на наборе множеств S

, S

, . . . , S

— это множество R

. . . S

n-ок элементов S

, . . . S

. Если s

, . . . , s

R, где s

, . . . s

, то говорится,

что s

, . . . s

связаны отношением R.

Определение 2.1.4 Одноместное отношение на множестве S называется предикатом на S. Гово-

рится, что P истинен на s S, если s P . Чтобы подчеркнуть эту интуицию, часто мы будем

писать P s вместо s P , рассматривая P как функцию, переводящую элементы S в истинностные

значения.

Определение 2.1.5 Двуместное отношение R на множествах S и T называется бинарным отноше-

нием. Часто мы будем писать s R t вместо s, t R. Если S и T совпадают (назовем это множество

U), мы будем говорить, что R — бинарное отношение на U .

Определение 2.1.6 Чтобы облегчить чтение, многоместные (трех- и более) отношения часто за-

писываются в «смешанном» синтаксисе, когда элементы отношения разделяются последовательно-

стью символов, и эти символы вместе образуют имя отношения. Например, отношение типизации

для простого типизированного лямбда-исчисления из Главы 9 записывается как Γ s : T — такая

формула означает «тройка Γ, s, T находится в отношении типизации».

Определение 2.1.7 Областью определения отношения R между множествами S и T называется

множество элементов s S, таких. что s, t R для какого-либо t. Область определения R обозна-

чается dom R . Областью значений R называется множество элементов t T , таких, что s, t R

для какого-либо s. Область значений R обозначается range R .

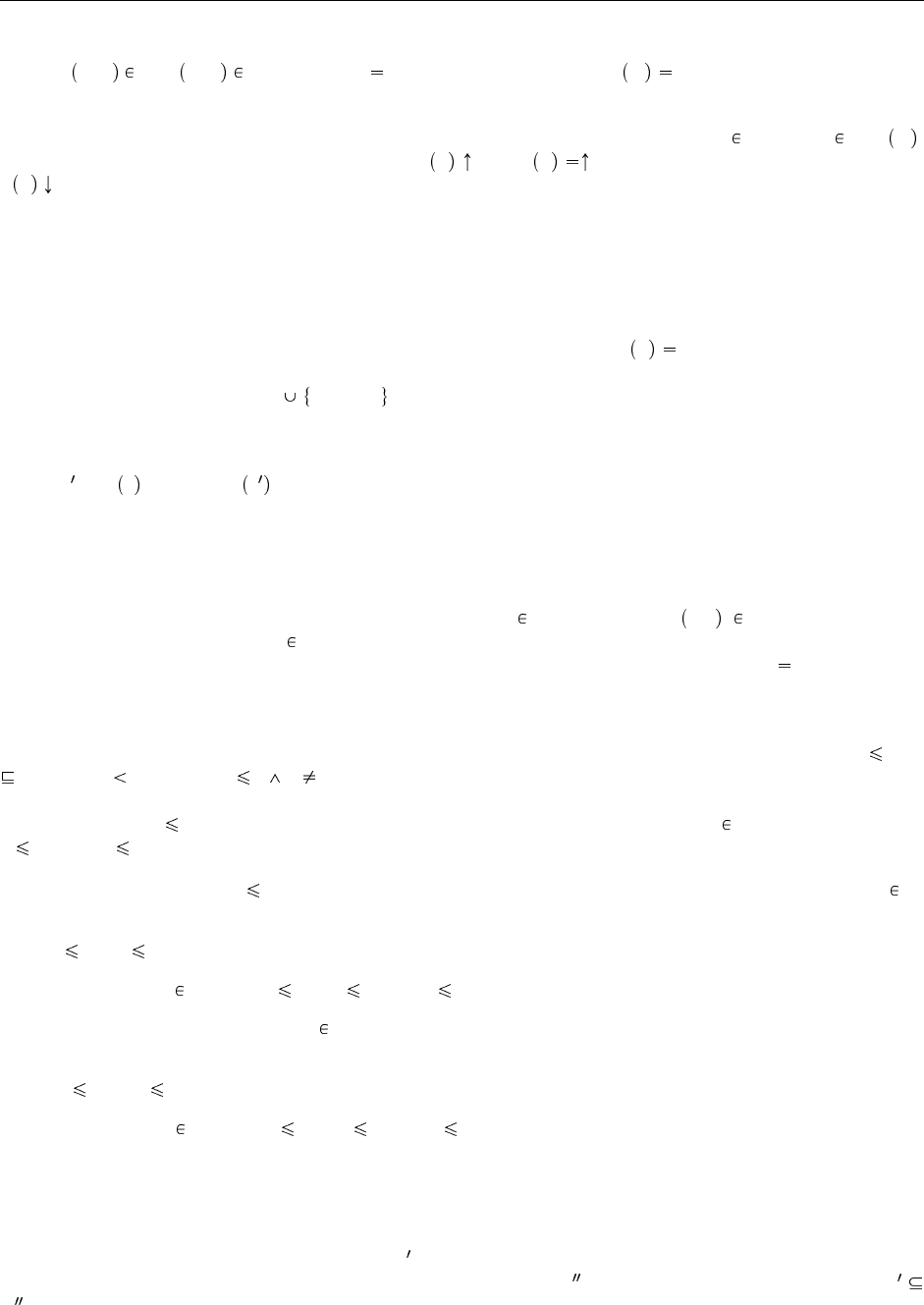
22 2.2. Упорядоченные множества

Определение 2.1.8 Отношение R на множествах S и T называется частичной функцией из S в T ,

если из s, t

R и s, t

R следует t

. Если, кроме того, dom R S, то R называется всюду

определенной (тотальной) функцией, или просто функцией, из S в T .

Определение 2.1.9 Частичная функция R из S в T определена на аргументе s S, если s dom R ,

и не определена в противном случае. Запись f x или f x означает «f не определена на x», а

f x означает «f определена на x».

В некоторых главах, посвященных программной реализации систем типов, нам также потре-

буется определять функции, которые на некоторых аргументах терпят неудачу (см., например,

Рис. 22.2). Важно отличать неудачу (частный случай разрешенного, наблюдаемого результата) от

расхождения; функция, способная потерпеть неудачу, может быть либо частичной (т. е., может

также расходиться), либо всюду определенной (т. е., она всегда либо возвращает результат, либо

терпит неудачу) — в сущности, часто нам будет нужно доказывать тотальность такой функции.

Если f возвращает неудачу при применении к x, мы будем писать f x неудача.

С формальной точки зрения, функция из S в T , которая может вернуть неудачу, является на

самом деле функцией из S в T неудача (мы предполагаем, что неудача не входит во множество

T ).

Определение 2.1.10 Пусть R — бинарное отношение на множестве S, а P — предикат на S. Если

из s R s и P s следует P s , то говорится, что R сохраняет P .

2.2. Упорядоченные множества

Определение 2.2.1 Бинарное отношение R на множестве S рефлексивно, каждый элемент S связан

отношением R с самим собой — то есть, для всех s S, s R s (или s, s R). Отношение R

симметрично, если для всех s, t S из s R t следует t R s. Отношение R транзитивно, если из s R t и

t R u следует s R u. Отношение R антисимметрично, если из s R t и t R s следует s t.

Определение 2.2.2 Рефлексивное и транзитивное отношение R на множестве S называется пред-

порядком на S. (Всякий раз, когда мы говорим о «предупорядоченном множестве S», мы имеем в

виду какой-то конкретный предпорядок на S.) Предпорядки обычно обозначаются символами или

. Запись s t значит s t s t.

Если предпорядок (на S) антисимметричен, то он называется частичным порядком на S. Ча-

стичный порядок называется линейным порядком на S, если для любых s, t S выполняется либо

s t, либо t s.

Определение 2.2.3 Пусть — частичный порядок на S, а s и t — элементы S. Элемент j S

называется объединением (или точной верхней гранью) s и t, если

1. s j и t j, а также

2. для всякого k S, если s k и t k, то j k.

Подобным образом, элемент m S называется пересечением (или точной нижней гранью) s и t,

если

1. m s и m t, а также

2. для всякого n S, если n s и n t, то n m.

Определение 2.2.4 Рефлексивное, симметричное и транзитивное отношение на множестве S назы-

вается отношением эквивалентности на S.

Определение 2.2.5 Пусть R — бинарное отношение на множестве S. Рефлексивное замыкание R —

это наименьшее рефлексивное отношение R , содержащее в себе R. («Наименьшее» здесь означает,

что, если имеется какое-то другое рефлексивное отношение R , включающее все пары из R, то R

R .) Подобным образом, транзитивное замыкание R — это наименьшее транзитивное отношение

rev. 104

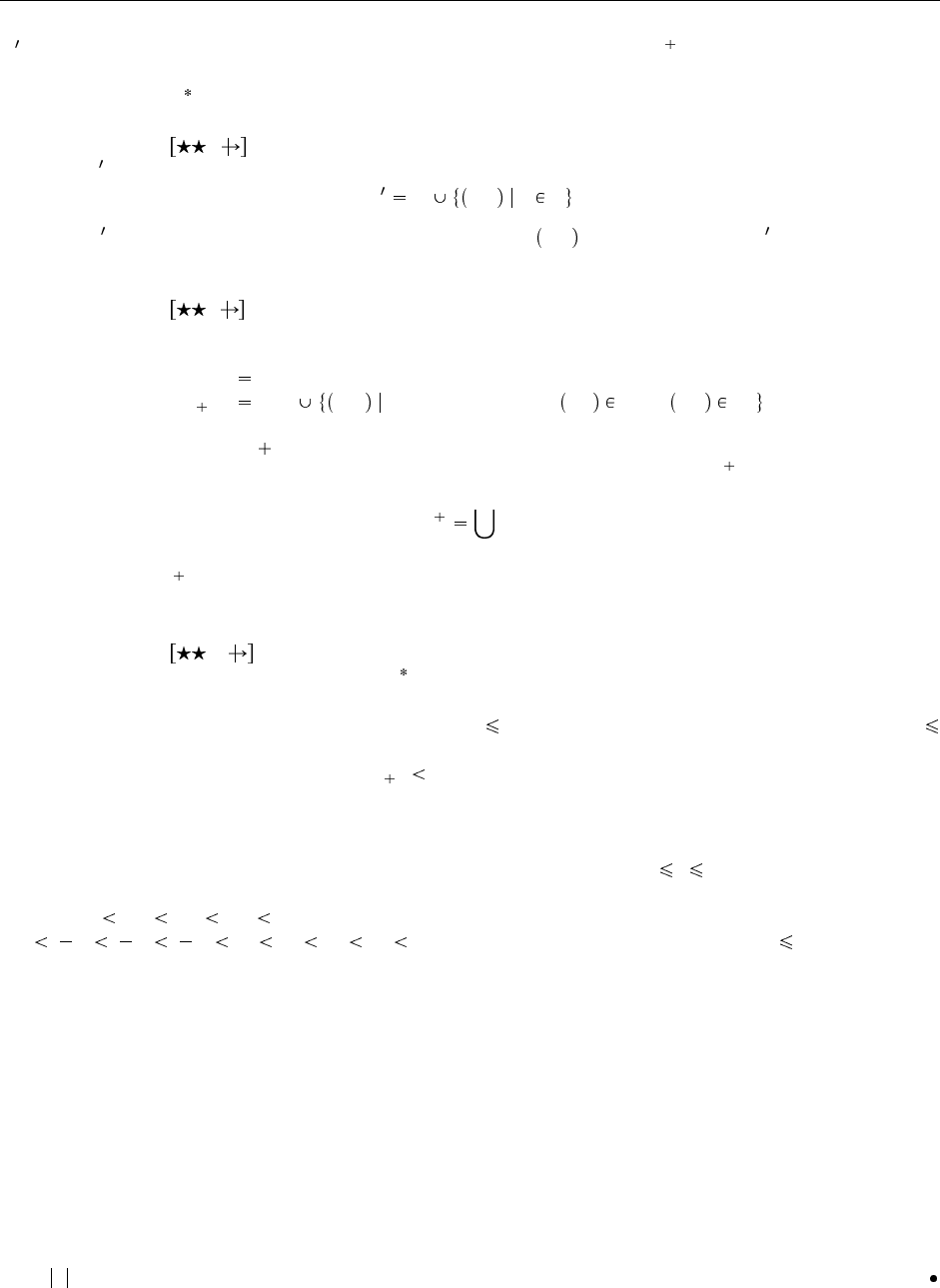
2.3. Последовательности 23

R , содержащее R. Часто транзитивное замыкание R обозначается R . Рефлексивно-транзитивное

замыкание R — это наименьшее рефлексивное и транзитивное отношение, содержащее R. Часто

оно обозначается R .

Упражнение 2.2.6 Предположим, нам дано отношение R на множестве S. Определим от-

ношение R так:

R R s, s s S

То есть, R содержит все пары из R плюс все пары вида s, s . Покажите, что R является рефлек-

сивным замыканием R.

Упражнение 2.2.7 Вот более конструктивный способ определить транзитивное замыкание

отношения R. Сначала мы определяем следующую последовательность множеств пар:

i 1

s, u для какого-либо t, s, t R

и t, u R

То есть, на каждом шаге i 1 мы добавляем к R

все пары, которые можно получить «за один шаг

транзитивности» из пар, входящих в R

. Наконец, определим отношение R как объединение всех

Покажите, что R на самом деле является транзитивным замыканием R — т. е., что оно удовле-

творяет условиям, заданным в Определении 2.2.5

Упражнение 2.2.8 Пусть R — бинарное отношение на множестве S, и это отношение

сохраняет предикат P . Докажите, что R также сохраняет P .

Определение 2.2.9 Пусть у нас есть предпорядок на множестве S. Убывающая цепочка на

есть последовательность s

, s

, . . . элементов S, такая, что каждый элемент последовательно-

сти строго меньше предшествующего: s

i 1

для всякого i. (Цепочки могут быть конечными или

бесконечными, однако для нас представляют больший интерес бесконечные, как видно из следующего

определения.)

Определение 2.2.10 Пусть у нас есть множество S с предпорядком . называется полным, ес-

ли он не содержит бесконечных убывающих цепочек. Например, обычный порядок на натуральных

числах, 0 1 2 3 . . ., является полным, а тот же самый порядок на целых числах,

. . . 3 2 1 0 1 2 3 . . . — нет. Иногда мы не упоминаем явно и просто

называем S вполне упорядоченным множеством.

2.3. Последовательности

Определение 2.3.1 Последовательность записывается путем перечисления элементов через запятую.

Запятая используется как для добавления элемента к последовательности в начало (вроде лиспов-

ского cons) или конец, так и для склеивания двух последовательностей (вроде лисповского append).

Например, если символ a обозначает последовательность 3, 2, 1, символ b обозначает последователь-

ность 5, 6, то 0, a — это последовательность 0, 3, 2, 1, запись a, 0 обозначает последовательность

3, 2, 1, 0, а запись b, a обозначает 5, 6, 2, 3, 1. (Использование запятой для двух разных операций — ана-

логов cons и append, — не создает путаницы, если нам не нужно вести речь о последовательностях

последовательностей.) Последовательность чисел от 1 до n обозначается 1..n (через две точки). За-

пись a означает длину последовательности a. Пустая последовательность обозначается знаком

или пробелом. Одна последовательность называется перестановкой другой, если они содержат одни

и те же элементы, возможно, в разном порядке.

rev. 104

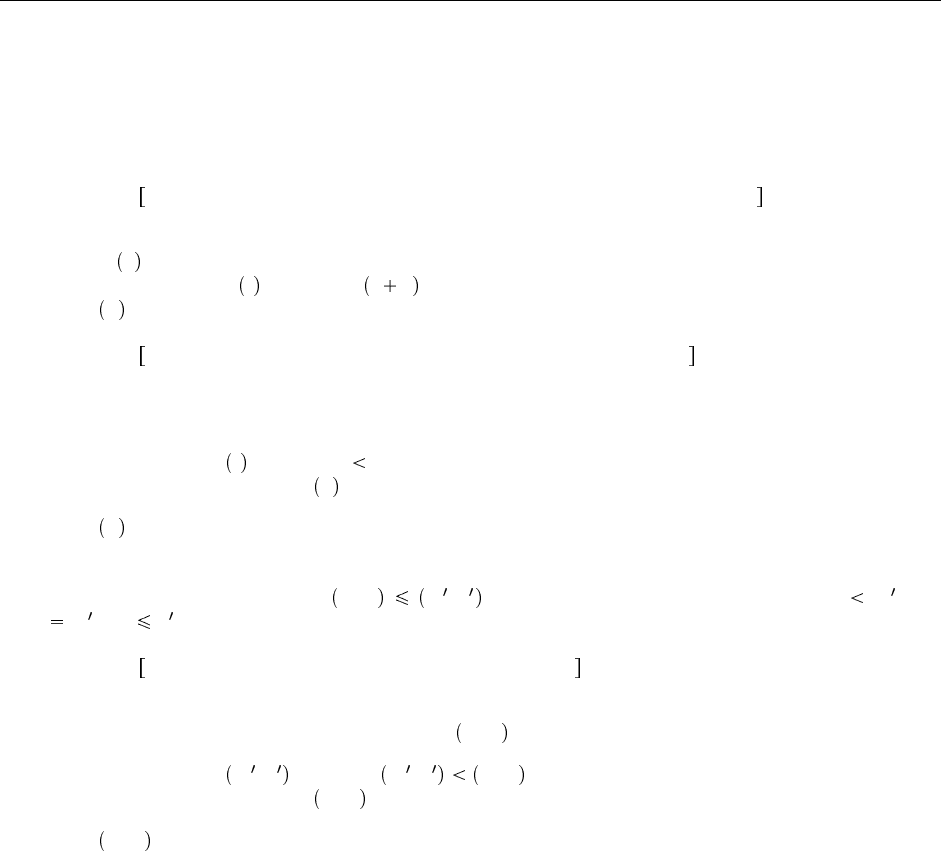
24 2.4. Индукция

2.4. Индукция

Доказательства по индукции встречаются в теории языков программирования очень часто, как и в

большинстве разделов информатики. Многие из этих доказательств основаны на одном из следуюших

принципов:

Аксиома 2.4.1 Принцип обыкновенной индукции на натуральных числах Пусть P — преди-

кат, заданный на множестве натуральных чисел. Тогда

Если P 0

и для любого i, из P i следует P i 1 ,

то P n выполняется для всех n.

Аксиома 2.4.2 Принцип полной индукции на натуральных числах Пусть P — предикат от

натуральных чисел. Тогда

Если для каждого натурального числа n,

предполагая P i для всех i n,

мы можем показать P n ,

то P n выполняется для всех n.

Определение 2.4.3 Лексикографический (или «словарный») порядок на парах натуральных чисел

определяется следующим образом: m, n m , n тогда и только тогда, когда либо m m , ли-

бо m m и n n .

Аксиома 2.4.4 Принцип лексикографической индукции Пусть P — предикат от пар нату-

ральных чисел. Тогда

Если для каждой пары натуральных чисел m, n ,

предполагая P m , n для всех m , n m, n ,

мы можем показать P m, n ,

то P m, n выполняется для всех m, n.

Принцип лексикографической индукции служит основой для доказательств со вложенной индук-

цией, где какой-либо пункт индуктивного доказательства использует индукцию «внутри себя». Этот

принцип можно распространить на индукцию по тройкам, четверкам и т. д. (Индукция по парам нуж-

на достаточно часто; по тройкам она иногда оказывается полезной; по четверкам и далее почти не

встречается.)

В Теореме 3.3.4 вводится еще один вариант доказательств по индукции, называемый структурная

индукция. Он особенно хорош, когда доказываются утверждения о древовидных структурах вроде

термов или деревьях вывода типов. Математические основания индуктивных рассуждений будут более

подробно рассмотрены в Главе 21. Мы увидим, что все упомянутые принципы индукции являются

частными проявлениями единой более общей идеи.

2.5. Справочная литература

Если понятия, перечисленные в этой главе, оказались для Вас незнакомыми, вероятно, имеет смысл

ознакомиться со справочной литературой. Существует множество вводных курсов. В частности, книга

Винскела (Winskel 1993) помогает развить интуицию в вопросах индукции. Начальные главы в книге

Дейви и Пристли (Davey and Priestley 1990) содержат замечательный обзор по упорядоченным множе-

ствам. Хэлмос (Halmos 1987) служит хорошим введением в базовую теорию множеств.

rev. 104

2.5. Справочная литература 25

Доказательство — это

воспроизводимый опыт в деле

убеждения.

Джим Хорнинг

rev. 104

26 2.5. Справочная литература

rev. 104

Часть I

Бестиповые системы

Глава 3

Бестиповые арифметические

выражения

Чтобы вести подробный разговор о системах типов и их свойствах, нам для начала нужно научиться

формальным образом работать с некоторыми более простыми характеристиками языков программи-

рования. В частности, требуются четкие, ясные и математически точные механизмы, чтобы описывать

синтаксис и семантику программ и строить о них рассуждения.

В этой и следующей главе мы разрабатываем такие механизмы для маленького языка, работающего

с числами и логическими значениями. Сам язык настолько прост, что почти не стоит рассмотрения,

однако с его помощью мы вводим некоторые базовые понятия — абстрактный синтаксис, индуктивные

определения и доказательства, вычисление и моделирование ошибок времени выполнения. В главах

с 5 по 7 те же самые шаги проделываются для намного более мощного языка — бестипового лямбда-

исчисления. Кроме того, там нам приходится иметь дело со связыванием имен и подстановками. Далее,

в Главе 8, мы начинаем собственно изучение типов, возвращаясь к простому языку из этой главы и с

его помощью вводя основные понятия статической типизации. В Главе 9 эти понятия распространяются

на лямбда-исчисление.

3.1. Введение

В языке этой главы имеется лишь несколько синтаксических конструкций: булевские константы

true (истина) и false (ложь), условные выражения, числовая константа 0, арифметические операции

succ (следующее число) и pred (предыдущее число) и операция-тест iszero, которая возвращает true,

будучи применена к 0, и false, когда применяется к любому другому числу. Эти конструкции можно

компактно описать следующей грамматикой.

t ::= термы:

true константа «истина»

false константа «ложь»

if t then t else t условное выражение

0 константа «ноль»

succ t следующее число

pred t предыдущее число

iszero t проверка на ноль

Правила, которыми мы пользуемся при записи этой грамматики (и при записи грамматик на протяже-

нии всей этой книги) близки к стандартной форме Бэкуса-Наура (см. Aho, Sethi and Ullman, 1986). В

первой строке (t ::=) объявляется, что мы определяем множество термов, и что мы будем употреб-

В этой главе изучается бестиповое исчисление логических значений и чисел (Рис. 3.2 на стр. 41). Соответствующая

реализация на OCaml хранится в веб-репозитории под именем arith и описывается в Главе 4. Указания, как скачать и

построить программу проверки, находятся по адресу http://www.cis.upenn.edu/~bcpierce/tapl.

30 3.1. Введение

лять букву t для обозначения произвольного терма. Всюду, где встречается символ t, можно подставить

любой терм. Курсив справа — просто комментарии.

Символ t в правых частях правил грамматики называется метапеременной. Это переменная в

том смысле, что t служит в качестве заместителя какого-нибудь конкретного терма, но это «мета»-

переменная, поскольку она является переменной не объектного языка — простого языка программиро-

вания, чей синтаксис мы сейчас описываем, — а метаязыка, — знаковой системы, которая служит для

описания. (На самом деле, в нашем теперешнем объектном языке даже нет переменных; мы их вве-

дем в Главе 5.) Приставка meta- происходит из мета-математики, отрасли логики, которая изучает

математические свойства систем, предназначенных для математических и логических рассуждений (в

частности, языков программирования). Оттуда же происходит термин метатеория; он означает сово-

купность истинных утверждений, которые мы можем сделать о какой-либо логической системе (или о

языке программирования), а в расширенном смысле — исследование таких утверждений. Таким обра-

зом, выражения вроде «метатеория наследования» в этой книге могут пониматься как «формальное

исследование свойств систем с наследованием».

На протяжнии этой книги мы будем использовать метапеременную t, а также близкие к ней буквы,

скажем, s, u и r, и варианты вроде t

или s , для термов объектного языка, которым мы занимаемся

в данный момент; далее будут введены и другие буквы для обозначения выражений других синтак-

сических категорий. Полный список соглашений по использованию метапеременных можно найти в

Приложении B.

Пока что слова терм и выражение обозначают одно и то же. Начиная с Главы 8, когда мы станем

изучать исчисления, обладающие более богатым набором синтаксических категорий (таких, как типы),

словом выражение мы будем называть любые синтаксические объекты (в том числе выражения-термы,

выражения-типы, выражения-виды и т. п.), а терм будет употребляться в более узком смысле, для

конструкций, которые обозначают вычисления (т. е., выражения, которые можно подставить вместо

метапеременной t).

Программа на нашем нынешнем языке — это всего лишь терм, построенный при помощи перечис-

ленных выше конструкций. Вот несколько примеров программ, вместе с результатами их вычисления.

Для краткости мы используем стандартные арабские цифры для записи чисел, которые формально

представляются как набор вложенных применений операции succ к 0. Например, succ(succ(succ(0)))

записывается как 3.

if false then 0 else 1;

is zero ( pred ( succ 0));

true

Символом |> на протяжении всей книги обозначаются результаты вычисления примеров. (Для кратко-

сти результаты опускаются, когда они очевидны или не играют никакой роли.) При верстке результаты

автоматически вставляются реализацией системы, которая в данный момент рассматривается (в этой

главе arith); напечатанные результаты представляют собой настоящий вывод системы.

Составные аргументы succ, pred и iszero в примерах приведены, для удобства чтения, в скобках.

Скобки не упоминаются в грамматике термов; она определяет только абстрактный синтаксис. Разу-

меется, присутствие скобок или их отсутствие играет весьма малую роль в чрезвычайно простом языке,

с которым мы сейчас имеем дело: обычно скобки служат для разрешения неоднозначностей в грамма-

тике, но в нашей грамматике неоднозначностей нет — любая последовательность символов может быть

разобрана максимум одним способом. Мы вернемся к обсуждению абстрактного синтаксиса и скобок в

Главе 5 (стр. 50).

При верстке перевода это правило не соблюдалось. — прим. перев.

На самом деле интерпретатор, которым обрабатывались примеры из этой главы (на сайте книги он называется arith)

требует скобок вокруг составных аргументов succ, pred и iszero, даже несмотря на то, что их можно однозначно разо-

брать и без скобок. Это сделано для совместимости с последующими исчислениями, где подобный синтаксис используется

при применении функций к аргументам.

rev. 104