Пинчук С.И. Организация эксперимента при моделировании и оптимизации технических систем

Подождите немного. Документ загружается.

221

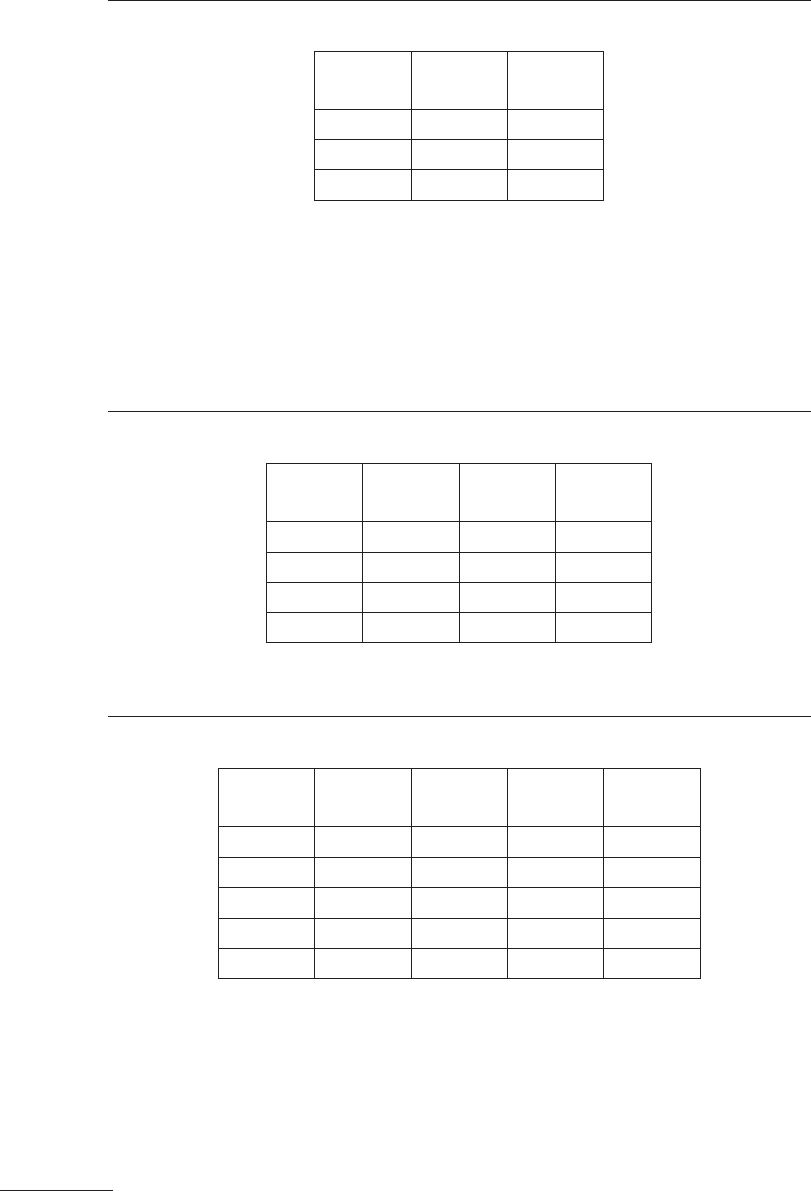
Рассмотрим правильный симплекс 1-3-6. В таблице 9.2 приведе-

ны условия первой серии опытов.

Таблица 9.2

Матрица симплекса

1-3-6

№

1 –1 –1

3 +1 –1

6 0 +0,73

Аналогичные симплексы можно построить на любой из 4-х сто-

рон квадрата.

Рассмотрим правильный симплекс

2-7-8. В таблице 9.3 приведе-

ны условия первой серии опытов.

Таблица 9.3

Матрица симплекса

2-7-8

№

2 +1 +1

7 –1 +0,46

8 +0,46 –1

Аналогичных симплексов также можно построить четыре.

Это самые большие среди правильных симплексов внутри квад-

рата. Сторона квадрата в первом симплексе имеет длину 2, во вто-

ром – 2,07. Эффективность всей процедуры поиска оптимума за-

висит от размеров исходного симплекса. С этой точки зрения оба

симплекса практически эквивалентны. Но с точки зрения числа

уровней фактора, они различны. В матрице 1-3-6 фактор Х

варьи-

рует на 3-х уровнях, а Х

– на двух. В матрице 2-7-8 оба фактора име-

ют по три уровня. Иногда важно, чтобы число уровней было мини-

мальным.

Чем меньше в матрице дробных чисел, тем лучше. В матрице

1-3-6 такое число одно, а в матрице 2-7-8 – их два.

Итак, предпочитают план типа 1-3-6.

Если начало координат перенести в точку 1, единицу масштаба

выбрать равной стороне квадрата (т.е. увеличить вдвое), то получим

преобразованную матрицу симплекса 1-3-6 (табл. 9.4).

222

Таблица 9.4

Преобразованная матрица симплекса

1-3-6

№

опыта

1 0 0

2 1 0

3 0,5 0,86

Следовательно, всегда нужно следить за системой координат, в

которой записан план.

Ниже приведен перечень матриц (в кодированных координатах)

как практическая рекомендация для применения.

Таблица 9.5

План-матрица начального симплекса при числе факторов

k = 3

№

опыта

1 –1 –1 +1

2 +1 –1 –1

3 –1 +1 –1

4 +1 +1 +1

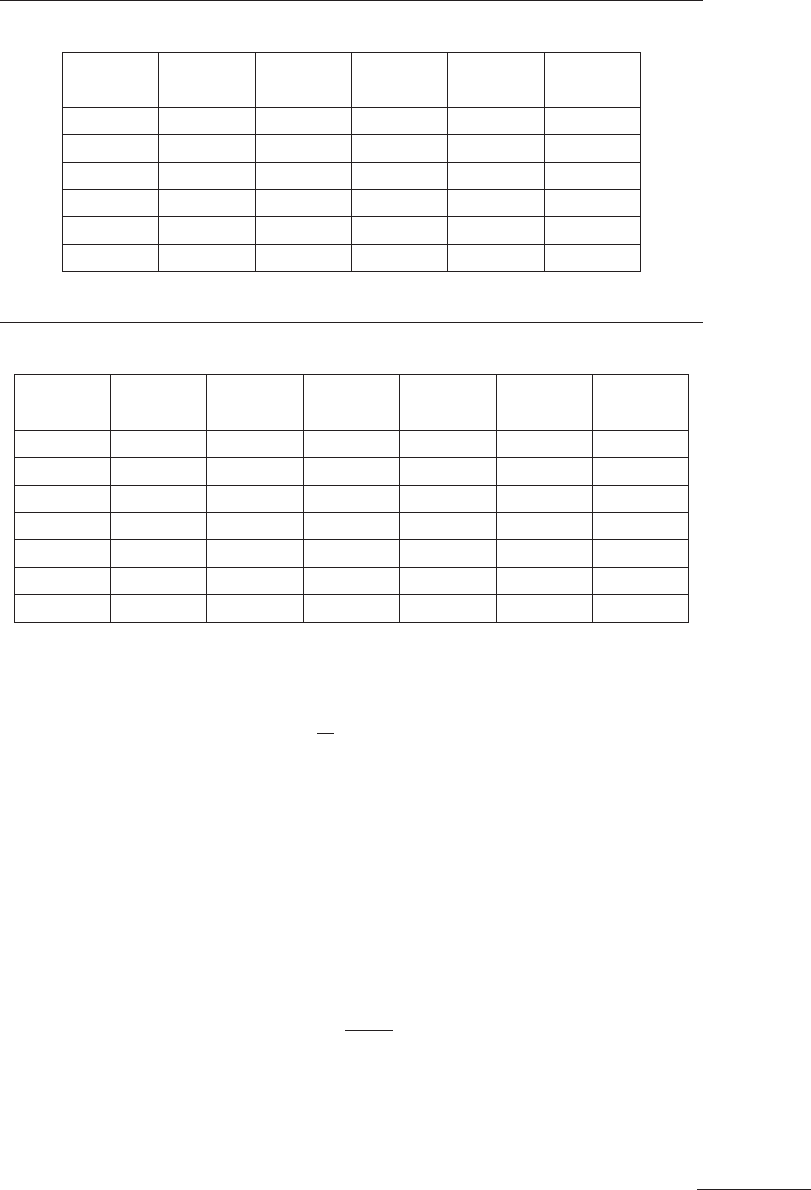
Таблица 9.6

План-матрица начального симплекса при числе факторов

k = 4

№

опыта

1 –1 +1 +1 +1

2 +1 –1 +1 +1

3 +1 +1 –1 +1

4 +1 +1 +1 –1

5 –0,618 –0,618 –0,618 –0,618

223

Таблица 9.7

План-матрица начального симплекса при числе факторов

k = 5

№

опыта

1 –1 +1 +1 +1 +1

2 +1 –1 +1 +1 +1

3 +1 +1 –1 +1 +1

4 +1 +1 +1 –1 +1

5 +1 +1 +1 +1 –1

6 –0,38 –0,38 –0,38 –0,38 –0,38

Таблица 9.8

План-матрица начального симплекса при числе факторов

k = 6

№

опыта

1 –1 +1 +1 +1 +1 +1

2 +1 –1 +1 +1 +1 +1

3 +1 +1 –1 +1 +1 +1

4 +1 +1 +1 –1 +1 +1

5 +1 +1 +1 +1 –1 +1

6 +1 +1 +1 +1 +1 –1

7 –0,215 –0,215 –0,215 –0,215 –0,215 –0,215

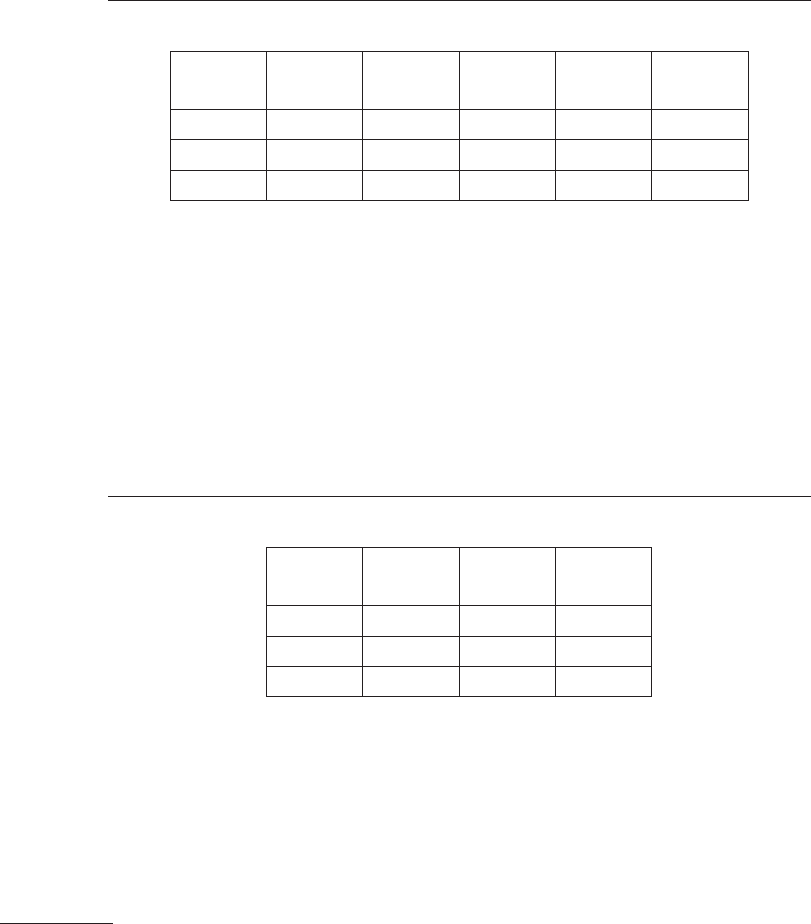
Для организации кантовки симплексов используют формулу:

1i=

x–x

∑

, (9.3)

где

– координата искомой вершины в натуральных единицах;

k – число факторов (следовательно, k + 1 – число вершин в исход-

ном симплексе);

* – i-я координата точки с наихудшим результатом.

Могут быть также использованы формулы 9.4 и 9.5.

= 2x

– x

* ; (9.4)

∑

;

(9.5)

где

– координата центра грани, относительно которой осуществляет-

ся отображение вершины симплекса с наихудшим результатом опыта;

– координата вершины, в которой получен наихудший результат.

224

Рассмотрим пример экспериментального поиска значений опти-

мизирующих факторов симплексным методом.

Изучался процесс сверления. Диаметр сверла – 0,5 мм. Материал –

Ст.45. Отклик – стойкость сверла в минутах. Варьировались: х

–

число оборотов в минуту, х

– подача в мм на оборот.

Из технологических соображений выбраны:

= 3050 об/мин; x

= 0,0036 мм/об;

∆x

= 1000 об/мин; ∆x

= 0,0006 мм/об;

Таблица 9.9

План-матрица начального симплекса

№

опыта

об/мин

мм/об

мин

1 –1 –1 2050 0,003 13,7

2 +1 –1 4050 0,003 21,5

3 0 +0,73 3050 0,004 32,6

Для первой кантовки симплекса определяем координаты новой

вершины 4 по формуле 9.3.

Отбрасываем вершину 1. По формуле 9.3 определяем коорди-

наты её зеркального отражения относительно стороны симплекса

2-3, т.е. координаты новой вершины 4 (см. рис. 9.9):

= 7100 – 2050 = 5050;

= 0,007 – 0,003 = 0,004.

Таблица 9.10

Координаты симплекса

2-3-4

№

опыта

об/мин

мм/об

мин

2 4050 0,003 21,5

3 3050 0,004 32,6

4 5050 0,004 25,9

При сопоставлении результатов приходим к выводу о необходи-

мости зеркального отображения вершины 2 относительно сторо-

ны 3-4 симплекса.

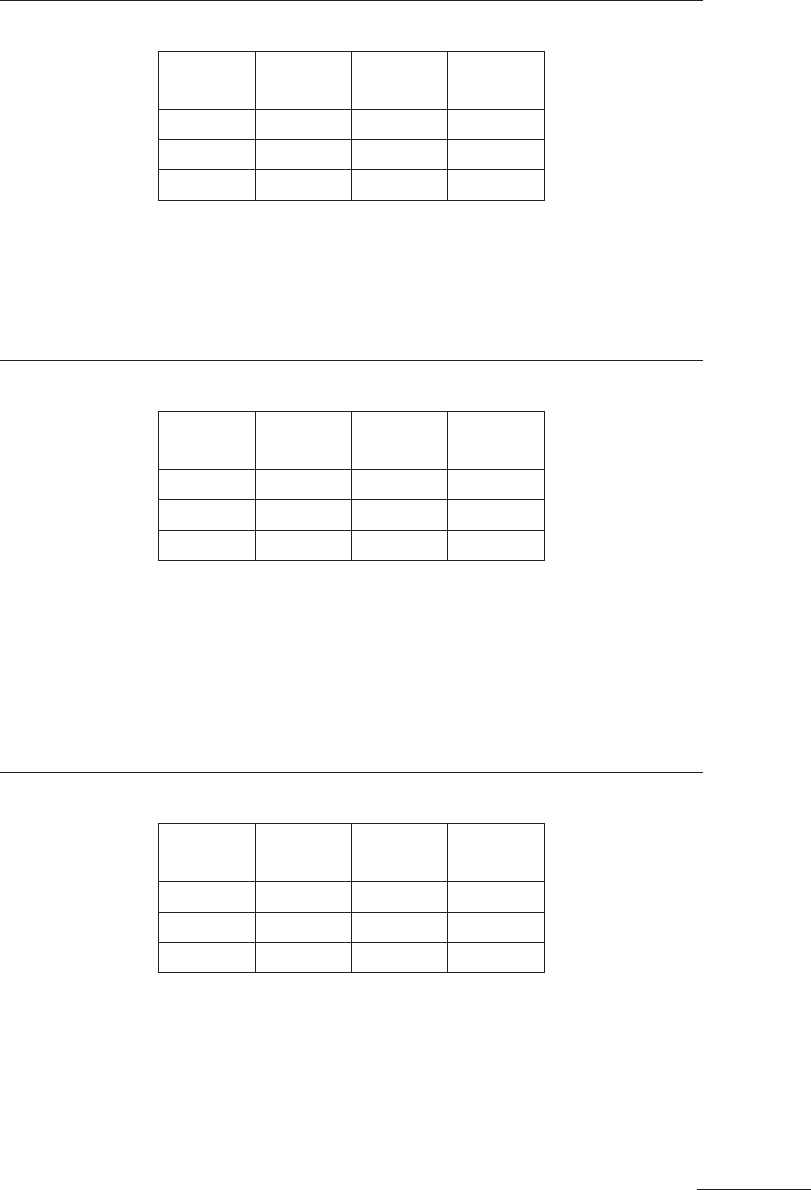
225

Таблица 9.11

Координаты симплекса

3-4-5

№

опыта

об/мин

мм/об

мин

3 3050 0,004 32,6

4 5050 0,004 25,9

5 4050 0,005 19,2

Возникло колебание симплекса.

Принимаем решение отобразить вершину 3 относительно сторо-

ны 2-4.

Таблица 9.12

Координаты симплекса

2-4-6

№

опыта

об/мин

мм/об

мин

2 4050 0,003 21,5

4 5050 0,004 25,9

6 6050 0,003 26,7

Итак, есть небольшое увеличение стойкости сверла по сравне-

нию с предыдущими результатами.

В последнем симплексе наихудший результат получен в вер-

шине 2. Осуществляем её зеркальное отображение относительно

стороны 4-6. Получаем новый симплекс 4-6-7.

Таблица 9.13

Координаты симплекса

4-6-7

№

опыта

об/мин

мм/об

мин

4 5050 0,003 25,9

6 6050 0,004 26,7

7 7050 0,003 62,0

В вершине 7 великолепный результат.

Продолжаем кантовать симплекс. Отображаем вершину 4 отно-

сительно его стороны

6-7.

226

Таблица 9.14

Координаты симплекса

6-7-8

№

опыта

об/мин

мм/об

мин

6 6050 0,003 26,7

7 7050 0,004 62,0

8 8050 0,003 62,0

Поскольку есть ограничения по числу оборотов, то кантовку

симплекса приходится прекратить. Полученные результаты имеют

важное практическое значение.

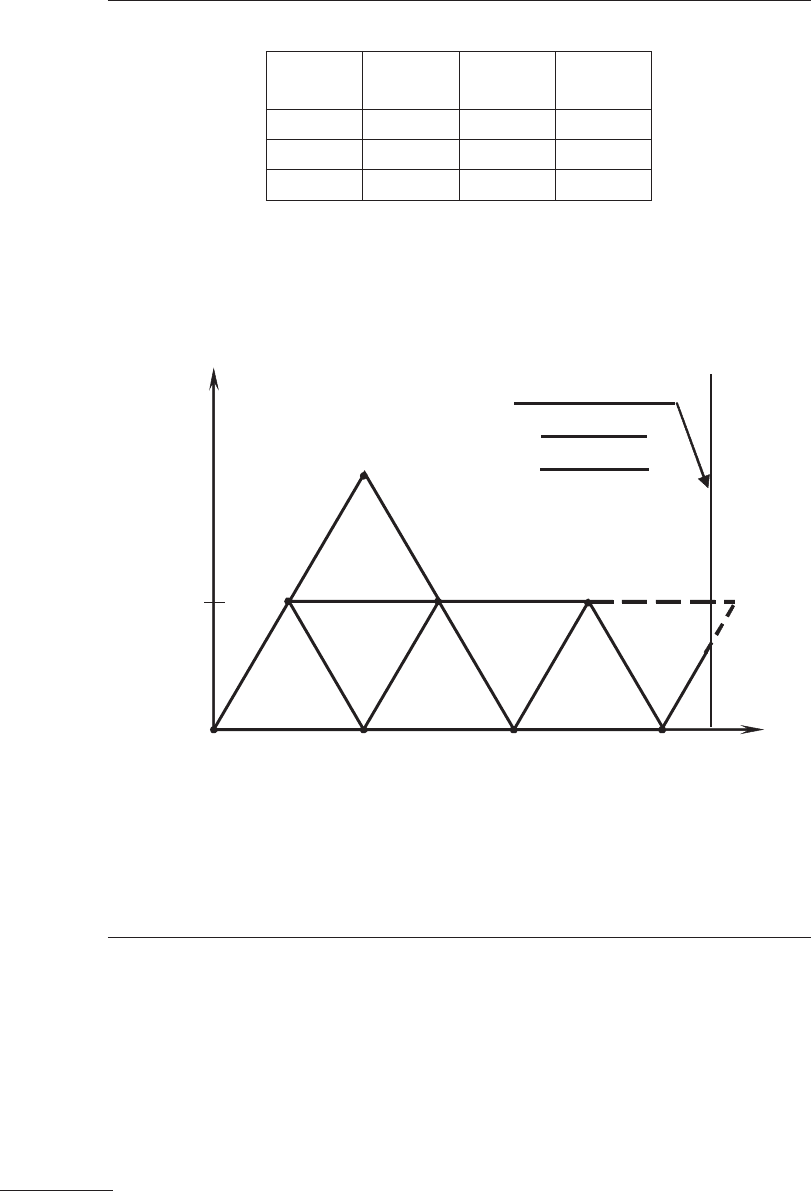
Схема «скитаний» симплекса представлена на рисунке 9.9.

Ограничение

по числу

оборотов

347

126

0,004

0,003

0,005

2050 40506050 8050

рис. 9.9 Схема «скитаний» симплекса

9.7 Градиентные методы экспериментальной

оптимизации

9.7.1 метод градиента

Метод градиента и его модификации – распространенные и эф-

фективные методы поиска оптимума.

Оптимум исследуемого объекта ищут в направлении наиболее

быстрого возрастания (или убывания) выходной переменной, т.е. в

направлении градиента.

227

Направление корректируют после каждого шага.

Графическая интерпретация градиентных методов поиска опти-

мума представлена на рисунке 9.10.

50%

60%

70%

80%

90%

рис. 9.10 Графическая интерпретация градиентных методов

поиска оптимума

Одна из модификаций градиентного метода экспериментальной

оптимизации – метод крутого восхождения (метод Бокса-Уилсона).

9.7.2

метод крутого восхождения

Задача метода крутого восхождения заключается в том, чтобы в

направлении наискорейшего возрастания (или убывания) выходной

переменной

Y осуществлять шаговое движение по градиенту.

Метод крутого восхождения объединяет в себе достоинства трёх

методов:

• ПФЭ или ДФЭ как средства для получения линейной математи-

ческой модели, используемой в качестве градиента;

• Гаусса-Зейделя;

• градиента.

Для определения направления движения используют адекват-

ную линейную регрессионную модель, которую находят при ПФЭ

или ДФЭ.

Направление движения при поиске оптимума корректируют не

после каждого следующего шага, а при достижении в некоторой

228

точке на данном направлении частного экстремума целевой функ-

ции (как в методе Гаусса-Зейделя).

В этой точке ставят новый ФЭ, вновь получают математическую

модель и, при необходимости, т.е. если полученная линейная мо-

дель адекватна, вновь осуществляют крутое восхождение по её на-

правлению.

Поиск прекращается, когда квадратичные эффекты в уравнении

регрессии становятся значимыми. Это указывает на то, что достиг-

нута область оптимума.

Начинать крутое восхождение следует от основных уровней зна-

чимых факторов, т.е. x

осн.

, x

осн.

, ..., x

осн.

Факторы изменяют пропорционально величинам коэффициен-

тов регрессии и с учетом их знаков «+» или «–».

Планирование движения по градиенту производят следующим

образом. По каждому фактору вычисляют произведения b

∆x

, т.е.

умножают коэффициент регрессии на интервал варьирования фак-

тора.

Находят фактор, для которого произведение b

∆x

наибольшее

по абсолютной величине. Будем называть этот фактор базовым;

· ∆x

)

max

= b

· ∆x

. Выбирают сдвиг в направлении крутого вос-

хождения по базовому фактору от основного уровня ∆x

* . Сдвиг

∆x

* может быть равен ∆x

или части этого интервала, т.е. μ∆x

(0 < μ < 1).

Строгих правил выбора величины ∆x

* нет. Её выбирает

исследователь.

Определяют величину коэффициентов пропорциональности K

по формуле (9.6):

Δxb

K =

(9.6)

т.е.

имеет знаки, соответствующие знакам соответствующих ко-

эффициентов регрессии.

Далее определяют величины шагов сдвига в направлении круто-

го восхождения для каждого i-того фактора K

по формуле:

∆x

* = ∆x

* · K

. (9.7)

При необходимости численные значения величин шагов округ-

ляют.

Вычисляют координаты первого шага крутого восхождения эк-

сперимента. Для этого полученное значение

∆x

* необходимо

229

алгебраически сложить с основным уровнем соответствующего i-го

фактора:

= x

осн.

+ . (9.8)

Далее последовательно прибавляют к предыдущей координате

соответствующего фактора очередной шаг крутого

∆x

* .

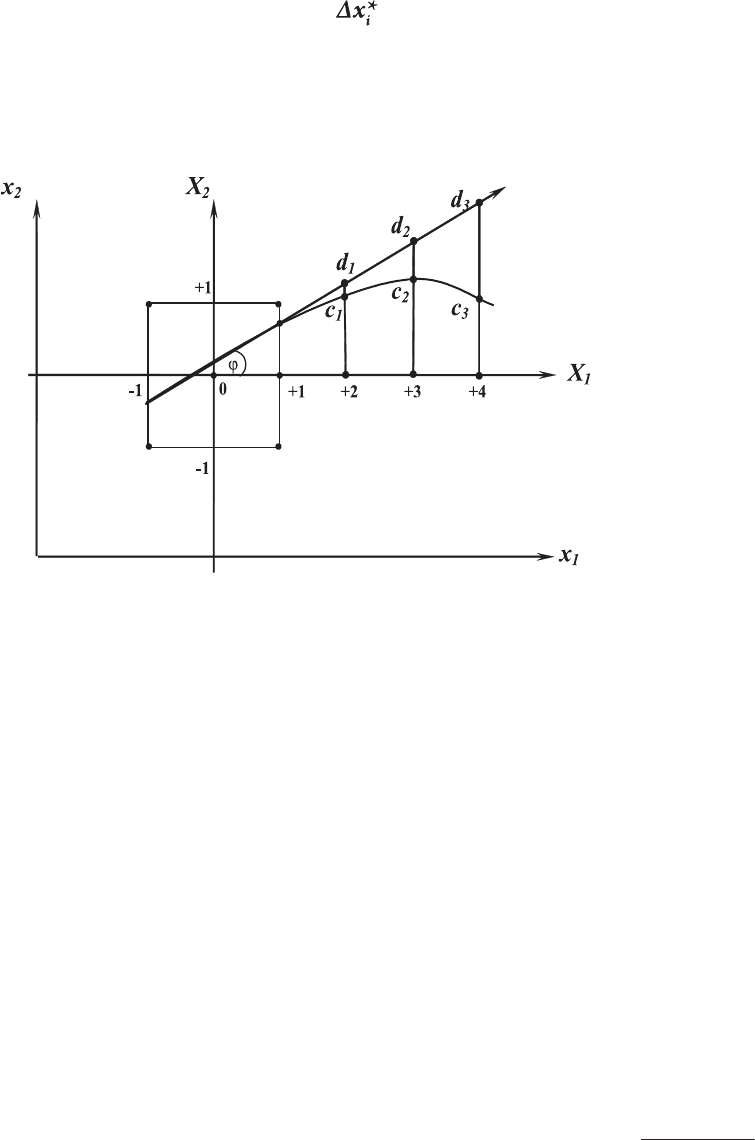
На рисунке 9.11 изображена схема крутого восхождения в об-

ласть экстремума (максимума) целевой функции.

рис. 9.11 Схема крутого восхождения в область экстремума

целевой функции

Если за пределами области варьирования факторов при ФЭ це-

левая функция имеет экстремум, то движение по градиенту, опре-

деляемому полученной при ФЭ адекватной линейной моделью,

приводит ко всё большим отклонениям от истинных значений по

мере удаления от нулевой точки.

Значения Y из опытов при значениях X

в точках с

, с

и т.д. будут

меньше предсказанных линейной моделью значений Ŷ, соответ-

ственно, в точках d

и d

и т.д. При этом c

< c

. Но в точке

результат опыта не только меньше рассчитанного по уравнению,

но и меньше предыдущего значения в точке с

. В этом случае вбли-

зи точки с

ставят новую серию опытов по новому плану ФЭ, по ре-

зультатам которой либо определяют новое направление движения

в область оптимума, если вновь полученная линейная модель адек-

ватна, либо прекращают движение.

230

Рассмотрим применение метода крутого восхождения на примере.

Выход продукта в процентах от исходного сырья зависит от

трех факторов: конечной температуры процесса

, скорости на-

грева х

и продолжительности изотермической выдержки х

Сначала осуществляем первую серию опытов по плану ПФЭ типа

для получения линейной модели. План-матрица ПФЭ и его ре-

зультаты приведены в таблице 9.15.

Таблица 9.15

План-матрица ПФЭ и его результаты

Уровни факторов и интервалы

варьирования

Нулевой уровень (X

= 0) 400 6 3

Интервал варьирования (∆x

) 15 0,5 1

Нижний уровень (Х

= –1) 385 5,5 2

Верхний уровень (Х

= +1) 415 6,5 4

План

Опыты:

1 – – – 10,5

2 + – – 8,3

3 – + – 6,8

4 + + – 4,6

5 – – + 16,4

6 + – + 14,2

7 – + + 12,7

8 + + + 10,5

По результатам опытов получена адекватная линейная модель:

Ŷ = 10,5 – 1,1 Х

– 1,85 Х

+ 2,95 Х

Пользуясь этим уравнением, планируем движение по градиенту

в область экстремума целевой функции. Расчеты для движения по

градиенту представлены в таблице 9.16.