Phadke A.G., Thorp J.S. Synchronized Phasor Measurements and Their Applications

Подождите немного. Документ загружается.

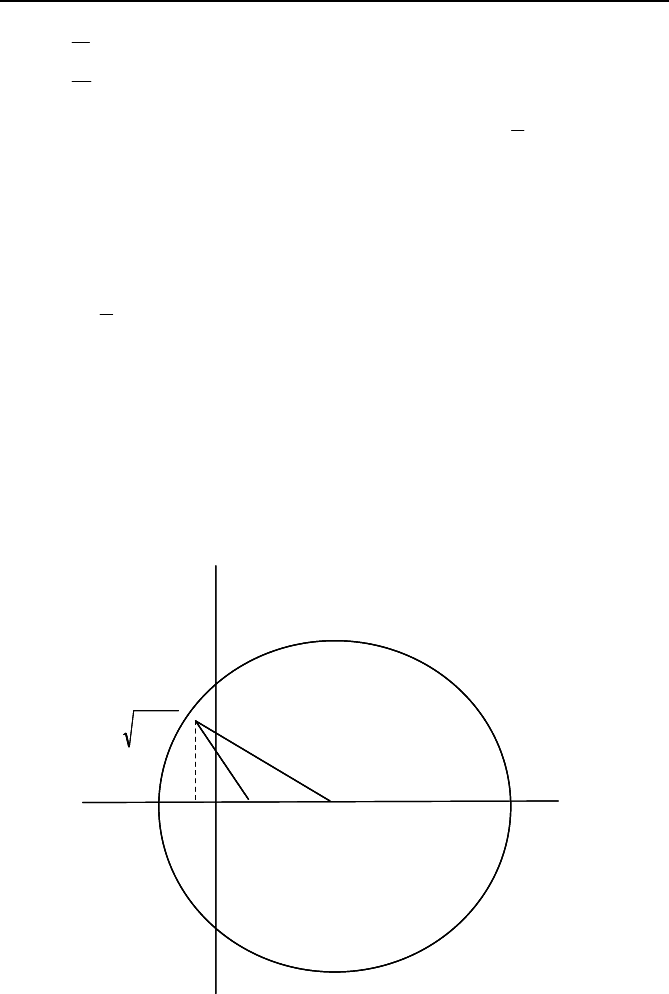
184 Chapter 8 Control with Phasor Feedback

.0)()(),,

,0)(),,(

≥+−−−−=

≥++−−=

ΛD(F)IFK

ΛD(F)IFD

zrzrzr(

zzrzr

(8.13)

The two matrices are obtained by mapping 8.11 into the

λ plane. Such an

F is called feasible. The system described by Eq. (8.11) is stable by its

very structure. The problem is that the low-frequency natural frequency

may have very small real parts. If we could find a matrix

F so that the ei-

genvalues

λ of Eq. (8.12) were in the region R

in Figure 8.12 we would

have guaranteed damping of low-frequency modes. A direct test for eigen-

values

λ in to be in R

in Figure 8.12 is quite difficult but a test for the ei-

genvalues,

λ in Figure 8.12 to be in the left half plane is simple. Hence the

mapping in Eq. (8.12) is used, recognizing that Eq. (8.13) is in the form

T22

00,

() 0 0,

ii i ij

zgurg

rz h v h

+≥=−=

−− ≥ = =

GBFB

HBFB

(8.14)

where

and v

are scalars depending on the geometry as shown in Figure

8.13, and

G and H are diagonal matrices. Conditions are given in [7] but

the numerical test is simply to apply the QR decomposition to the matrix

B, i.e. if

Fig. 8.13 The values of u

and v

for Eq. (8.14).

1 α−ω

ωα

r-z

1 α−ω

ωα

r-z

1 α−ω

ωα

r-z

8.4 Coordinated control of oscillations 185

⎡

⎤

⎢

⎥

⎣

⎦

(8.15)

where

T is orthogonal and R is upper triangular. Then Eq. (8.14) is equiva-

lent to

() () 0.

rz rz

⎡⎤

⎡⎤⎡⎤

+=+ ≥

⎢⎥

⎢⎥⎢⎥

⎣⎦⎣⎦

⎣⎦

⎡⎤

⎡⎤⎡⎤

−− = +− ≥

⎢⎥

⎢⎥⎢⎥

⎣⎦⎣⎦

⎣⎦

RFR

TGT F TGT

RFR

THT F THT

(8.16)

The fact that G and H are diagonal, combined with the assumption that

there are no open loop eigenvalues on the circle in Figure 8.11 allows one

remaining transformation. If there are no eigenvalues on the circle, then

in Eq. (8.17) is invertible:

;

−

⎡⎤⎡ ⎤

⎢⎥⎢ ⎥

−

⎣⎦⎣ ⎦

⎡⎤

−

⎢⎥

⎣⎦

11 12

T1T

12 22 22 12

11 12 22 12

MM I 0

TGT ; U

MM MMI

MMMM 0

UTGTU

(8.17)

HTT

=N, then the final conditions are that

[]

1211

−−−

−≥

≥

−

≥

RMMMMR

RNNNNR

(8.18)

If there are sufficient well-placed measurements and there is one feasi-

ble matrix F then F is not unique. The choice of optimal F as the one with

minimum Frobenius norm is suggested in [7]. The Frobenius norm of F is

given by 8.19:

186 Chapter 8 Control with Phasor Feedback

.min

⎟

⎠

⎞

⎜

⎝

⎛

∑∑

(8.19)

In [7] it is shown that if the problem is one of minimizing the norm in

Eq. (8.19) subject to the constraints of Eq. (8.18), one must compute the

Schur factorization of

11TTT

11 12 22 12

−−−

⎡⎤

−=

⎣⎦

MMMM SDS

(8.20)

In Eq. (8.20) S is orthonormal and D is diagonal. Replace the negative

entries on the diagonal of D with zero and call the result

D . If

then

−

−−

⎡⎤

≤−

⎣⎦

−

11T

11 12 22 12

SDS R N N N N R

FSDS

(8.21)

The minimum norm F obtained from Eq. (8.21) may, in fact, not be fea-

sible under some situations. Hence it is worth examining the closed loop

eigenvalues before using it. The conditions in Eq. (8.18) provide an inter-

val in which

F must lie. The matrix in Eq. (8.18) is a more reliable choice

for

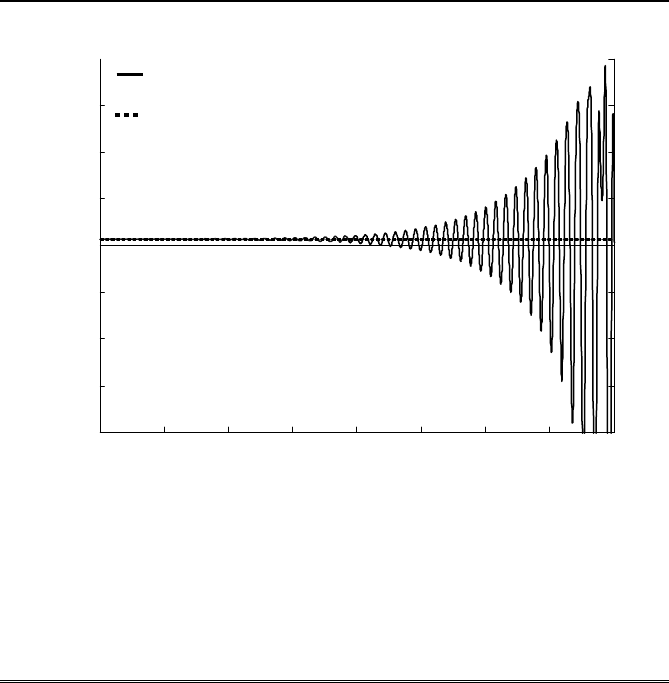
Example 8.5

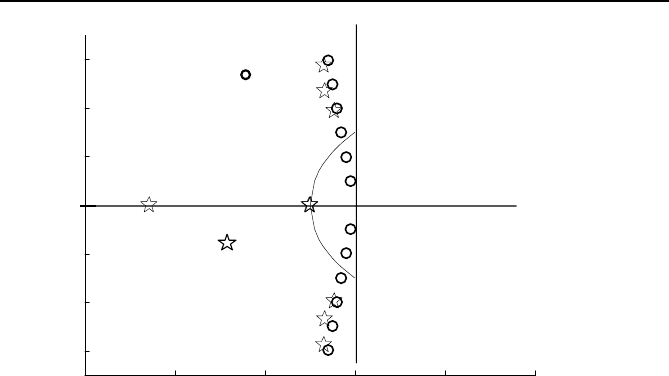
The Matlab file TAC92.m has a 12-dimensional system with eigenvalues

given in Table 8.3. The radius of the circle in Figure 8.3 is

r = 5 and the

center is at

= 4. The B matrix is also shown in Table 8.3. Using F = N

the closed loop eigenvalues are shown in Figure 8.14.

Table 8.3 Data for Matlab example

Eigenvalues B

Closed loop

–0.1 ± j1 3.6946 0.1730 0.1365 –9.3842

–0.2 ± j2 0.6213 1.9797 0.0118 –4.5731

–0.3 ± j3 0.7948 0.2714 2.8939 –0.6803

j5.7594

–0.4 ± j4 0.9568 0.2523 0.1991 –0.6741

j4.7032

–0.5 ± j5 0.5226 0.9757 0.2987 –0.4494

3.9404

–0.6 ± j6 0.8801 0.7373 0.6614 Four at –1.000

8.4 Coordinated control of oscillations 187

Fig. 8.14 Open and closed loop eigenvalues.

%TAC92.m 7-3-2007 Section 8.4

hold off

r=5;

z0=4;

w=[1 2 3 4 5 6];

B=[ 3.6946 0.1730 0.1365

0.6213 1.9797 0.0118

0.7948 0.2714 2.8939

0.9568 0.2523 0.1991

0.5226 0.8757 0.2987

0.8801 0.7373 0.6614];

A(1:6,1:6)=0*eye(6);

A(1:6,7:12)=eye(6);

A(7:12,1:6)=-diag(w.^2);

A(7:12,7:12)=-2*diag(.1*w);

% plot open nlop eigenvalues and the circle

xp=-.1*[1:11]+.1;

plot(eig(A),'ro')

axis([-8 4 -8 8])

-6 -4 -2 0 2 4

-6

-4

-2

Open loop

Closed loop

-6 -4 -2 0 2 4

-6

-4

-2

en loop

λ s

Closed loop λ

188 Chapter 8 Control with Phasor Feedback

hold on

plot(xp,sqrt(9+8*xp-xp.*xp),xp,-sqrt(9+8*xp-xp.*xp))

%Form the diagonal matrices G and H is Eq. (8.14)

G=0*eye(6);

H=G;

for i=1:6,

H(i,i)=w(i)^2-.2*w(i)+1;

G(i,i)=0.8*w(1)+w(i)^2-9;

end

% now the QR decomposition of B and the formation of M and N in

% Eqs. (8.17) and (8.18)

[T,RR]=qr(B);

M=T'*G*T;

MM(1:3,1:3)=M(1:3,1:3)-M(1:3,4:6)*inv(M(4:6,4:6))*M(4:6,1:3);

MM(4:6,4:6)=M(4:6,4:6);

eig(MM(4:6,4:6));

N=T'*H*T;

NN(1:3,1:3)=N(1:3,1:3)-N(1:3,4:6)*inv(N(4:6,4:6))*N(4:6,1:3);

NN(4:6,4:6)=N(4:6,4:6);

R=RR(1:3,1:3);

% M1 and N1 are the matrices in equation (8.18)

M1=(1/z0)*inv(R)*MM(1:3,1:3)*inv(R)';

N1=(1/(r-z0))*inv(R)*NN(1:3,1:3)*inv(R)';

% the Schur decomposition for the minimum norm F

[S,V]=schur(M1);

VV=V;

for i=1:3,

if(V(i,i) < 0), VV(i,i)=0; end

end

F=S*VV*S';

%Test eig(F-M1)

F=N1;

eig(G+4*B*F*B')

189

eig(H-B*F*B')

%Plot Closed loop eigenvalues

A(7:12,7:12)=A(7:12,7:12)-B*F*B';

plot(eig(A),'bx')

Example 8.6

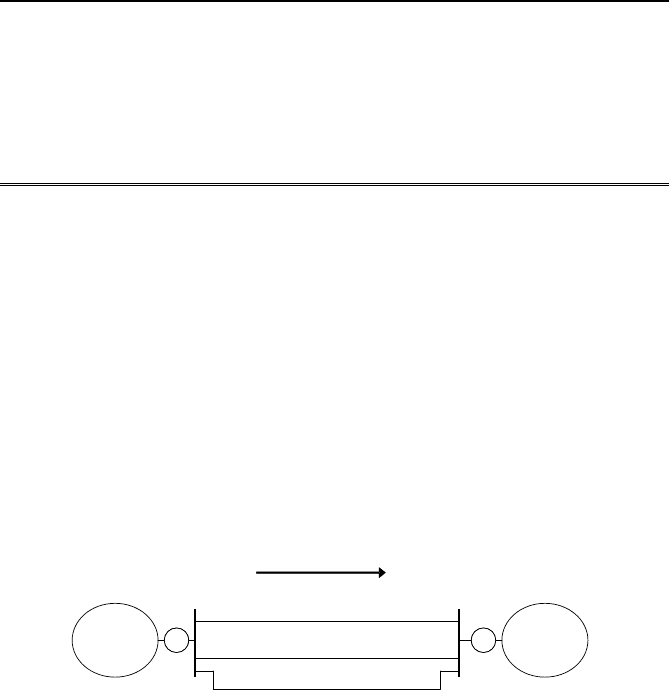
Joshua K. Wan

Fig. 8.15 The model two area system.

The HVDC line is modeled as two loads: one load connected to the bus at

each area interface. The amount of power drawn by one load is exactly

equal to the power supplied by the other load. The collocated control

scheme is to modulate the power flow along the line proportional to the

frequency difference between areas measured by the PMUs at either end of

the line. The frequency measurement taken at the remote bus (Area 2) is

subject to communications delay. Assuming a dedicated fiber-optic com-

munication channel connecting Areas 1 and 2 it is reasonable to assume that

the delay is less than 50 ms. Figure 8.17 shows the collocated controller

Area 1

Area 2

Line 1 220 km

Line 2 220 km

413 MW

HVDC Line

PMU PMU

8.4 Coordinated control of oscillations

The system in Figure 8.15 [4] is a four-generator two-area system used as

an example of a power system stabilizer (PSS) design. The four generators

are identical except for the inertias which are 6.5 s in Area 1 and 6.175 in

area 2. The two areas are connected by two 220-km 230 kV lines. Without

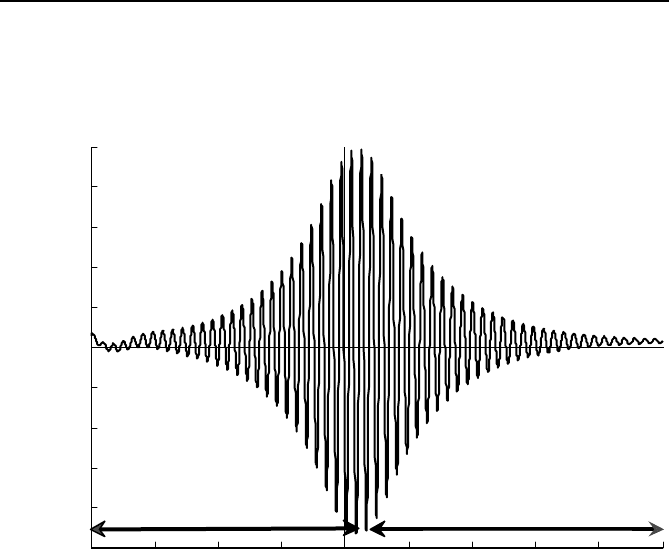
the stabilizer there is an unstable low-frequency interarea mode at 0.64 Hz.

The system has been modified [8] by adding a parallel HVDC line con-

necting the two areas. In [8] an artificial situation is created to study the ef-

fect of collocated control using the HVDC line. The situation studied is a

period with the PSS not in service and after the 0.64-Hz oscillation has

grown the PSS is inserted to damp the oscillation. The power flow between

the systems is shown in Figure 8.16

190 Chapter 8 Control with Phasor Feedback

performance with no delay. Delays up to 300 ms cause no noticeable deg-

radation in the performance.

Fig. 8.16 The power flow between areas when the PSS is inserted after 50 s.

The compelling reason to use the collocated scheme is its robustness. To

test the robustness the following system changes were made without

changing the control algorithm.

1. Increase system-wide loading by 50%:

A1: +50%, A2: +50%

A1: –50%, A2: –50%

A1: +50%, A2: –50%

A1: –50%, A2: +50%

2. Increase nominal power flow along DC tie by 100 MW.

3. Change the lengths of the AC tie lines by 10%.

4 Change the generator inertias:

Area 1: 7.5 s

Area 2: 5.175 s

10 20 30 40 50

70 80 90

100

413.2

413.25

413.3

413.35

413.4

413.45

413.5

413.55

413.6

413.65

413.7

Time

Power P, MW

Active power from Area 1 to Area 2

With PSS

No PSS

8.5 Discrete event control 191

Fig. 8.17 Performance of the collocated controller.

For all these simulations the communications delay was kept at a constant

50 ms. None of these system changes had any noticeable effect on the per-

formance of the controller.

8.5 Discrete event control

0 10

50 60 70 80

100

200

300

400

500

600

700

800

Time t (s)

Power P, MW

Active Power from Area 1 to Area 2:

Communications delay = 50 ms

no HVDC control

with HVDC control

All of the control in the previous sections has been continuous feedback

control, that is, the control, u(t), depends on the state, x(t), at each instant

of time. It x(t) changes then u(t) changes with a small delay induced by

communication latency (actually u(t)=f(x(t – Δt)). The power system,

however, has other types of control which can be characterized as discrete

in their dependence on state. These controls are typically stability controls

and are characterized by a specific action taken when the state exceeds a

limit. Examples are the use of the dynamic brake, high-speed switching of

series and shunt capacitors, high-speed generator tripping triggered by the

loss of the direct current (DC) line, and under-frequency and voltage load

shedding. The control action responds to the state but not continuously.

192 Chapter 8 Control with Phasor Feedback

An early phasor measurement application was of this form [9]. The at-

tempt was to control the power flow on the Intermountain and Pacific In-

tertie HVDC lines in a discrete form in response to a collection of ap-

proximately 20 phasor measurements which were to be communicated to

the Sylmar substation (the southern terminal of both DC lines). The control

action was limited to

± 500 MW ramps on each line. The measurement

Fig. 8.18 The WECC System for DC line control.

locations are shown in Figure 8.18. The locations were chosen in part to at-

tempt to get appropriate coverage of dynamic events but also in collabora-

tion with the participating utilities in terms of accessibility of the PMUs

and availability of communication channels. The power system model was

a 176-bus system with 29 generators that included the two DC lines.

The challenge, from a control perspective, is to find a technique that will

determine from the limited measurements which of the nine possibilities in

PMU

HVDC Terminal

Angle Measurement Unit

PMU

Phase

PMU

Sylmar

They are a form of discrete event control where state space has been parti-

tioned by some process. In most early stability controls of this type many

off-line simulations were performed in order to develop the rules for appli-

cation of the control.

8.5 Discrete event control 193

Table 8.4 is the correct choice. In attempting to select an approach it must

be recognized that the off-line calculations of the classical approach are

still appropriate; that is, the map from phasor measurements can be con-

structed from off-line simulations.

Table 8.4 Control options

Intermountain Pacific Intertie

0 0

0 +500 MW

0 –500 MW

+500 MW 0

+500 MW +500 MW

+500 MW –500 MW

–500 MW 0

–500 MW +500 MW

–500 MW –500 MW

8.5.1 Decision trees

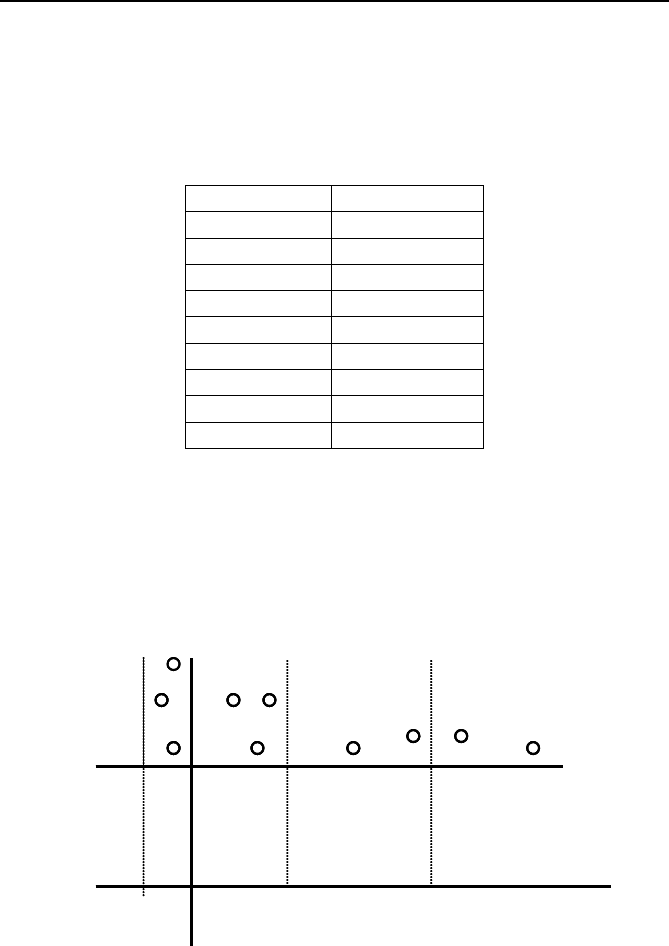
Consider the Xs and Os in the sequence of drawings in Figure 8.19. The

horizontal and vertical lines partition the (

x,y) plane into regions that are

either Xs or Os. The horizontal line at

y = 1.5 has all Xs below, the vertical

line at

y = –0.5 has all Xs to the left.

Fig. 8.19 Initial partitioning.

1.0 2.0

1.5

2.0

- 0.5

2.5

1.0 2.0

1.5

2.0

- 0.5

2.5

1.0 2.0

1.5

2.0

- 0.5

2.5