Peng S., Zhang J., Engineering Geology for Underground Rocks
Подождите немного. Документ загружается.


6.3 Finite element discretization of the poroelastic solution 135
³³
³³
w
w
:
w
w
:
w
w
:
w
w
:
::
S
fr
ma
dSd
dd
t
f
N
t
p
mNCDB
t
p
mNCDB
t
u
BDB
fr
frmf
T
ma
mamf
T
mf
T
D
D
(6.22)
or,
t
F
t
p
R
t
p
R
t
u
K
fr
2
ma
1
w
w
w
w
w
w
w
w
(6.23)
where detailed expressions of the coefficients are given in Appendix 6.2.
Using the Gaussian quadrature method (Zienkiewicz 1977), the double
porosity mass balance equations (last two equations in Eq. 6.10) in the
finite element forms can be given for each system.
For the rock matrix system:
³³³
³³
::
::
:
w
w
:
w
w
: :
ī
ma
ma
dīdd
dd
ma
TT
ma
T
mamf
T
mama
T
qNNǻpNN
t
p
NN
t
u
BCmDNpNkN
ZE
D
P
1
(6.24)
For the fracture system:
³³³
³³
::
::
:
w
w
:
w
w
: :
ī
fr
fr
dīdd
dd
fr
TT
fr
T
frmf
T
frfr
T
qNNǻpNN
t
p
NN
t
u
BCmDNpNkN
ZE
D
P
1
(6.25)
where
mafr
ppǻp , m
T
= (1 1 1 0 0 0);
*
is the domain surface on
which the fluid flux q is applied; and Biot’s effective stress coefficients,ҏ Į,
can be evaluated as:
fr
sk
fr
s
sk
ma
K
K
K
K
*
1
1
D
D
(6.26)

136 6 Double porosity poroelasticity and its finite element solution
where K
sk
and K
*
sk
are the bulk moduli of the skeleton for the matrix blocks
and the fractures, respectively; K
s
and K
fr
are the bulk moduli of the solid
grains and fractures, respectively; and the relative compressibilities,
E
, can
be written as:
n
frfr
f
fr
fr
s
mama
f
ma
ma
sK
n
sK
n
K
n
K
n
D
E
D
E
(6.27)
where K
f
and K
n
are the bulk modulus of the fluid and the normal stiffness
of the fractures, respectively; n is the porosity; and s is the fracture spac-
ing.
Equations 6.24 and 6.25 can be written as the following finite element
forms:
ma
ma
1frma11
Q
t
p
NQp)pL(Q
t
u
M
w
w
w
w
(6.28)
fr
fr
2fr2ma2
Q
t
p
N)pL(QQp
t
u
M
w
w
w
w
(6.29)
where detailed expressions of the above coefficients are listed in Appendix
6.2.
Equations 6.23, 6.28 and 6.29 represent a set of differential equations in
time and can be expressed in matrix form as follows:
»
»
»
»
»
¼
º
«
«
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
fr
ma
fr
ma
22
11
21
fr
ma
2
1
Q
Q
dt
dF
p
p
u
N0M
0NM
RRK
p
p
u
LQQ0
QLQ0
000
dt
d
(6.30)
The discretization in space has been completed, and Equation 6.30 now
represents a set of differential equations in time.
6.3.3 Finite element discretization in time
Using a fully implicit finite difference scheme in the time discretization
domain, such that:

6.3 Finite element discretization of the poroelastic solution 137
°
°
°
¯
°
°
°
®
'
'
'
)(
1
)(
1
)(
1
t
fr
ǻtt
fr
ǻtt
fr
t
ma
ǻtt
ma
ǻtt
ma
tǻtt
ǻtt
pp
p
pp
p
uu
u
tdt
d
tdt
d
tdt
d
(6.31)
and substituting Eq. 6.31 into Eq. 6.30, the finite element equations in the
matrix form for a double porosity poroelastic medium can be expressed as
follows:
ttt
t
tt
ǻtǻt
ǻt
ǻtǻt
ǻtǻt
ǻt
»
»
»
»
»
¼
º
«
«
«
«
«
¬
ª
»
»
»
»
»
¼
º
«
«
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
»
»
»
¼
º
«
«
«
¬
ª
'
'
0
0
0
0
1
1
F
Q
Q
F
p
p
u
NM
NM
RRK
p
p
u
N)L(QQM
QN)L(QM
RRK
fr
ma
fr
ma
22
11
21
fr
ma
222
111
21
(6.32)
There are 5 unknowns (u
x
, u
y
, u
z
, p
ma
, p
fr
) and 5 equations per node;
therefore, displacements and pressures can be solved. In addition, strains
and stresses can be obtained through the following equation and Eq. 6.6.
)(
2
1
,, ijjiij
uu
H
(6.33)
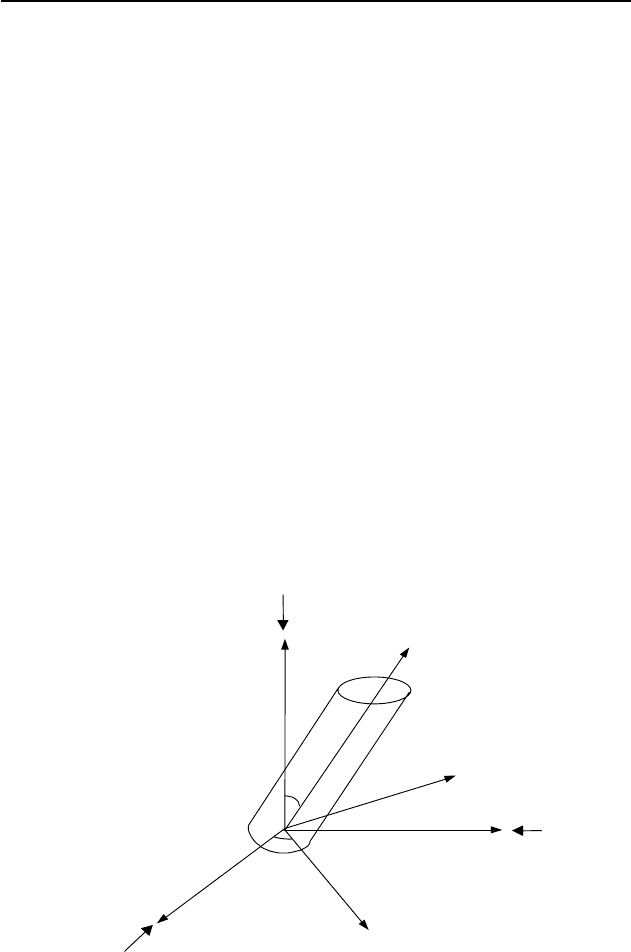
6.3.4 Stress conversion for an inclined borehole
For an inclined borehole with its axis inclined with respect to the principal
axes of the far-field stresses (see Fig. 6.2), the following equations can be
used to convert the global coordinate (far-field stress coordinate, xc, yc, zc)
into the local coordinate (borehole coordinate, x, y, z) system.
138 6 Double porosity poroelasticity and its finite element solution
°
¿
°
¾
½
°
¯
°
®
»
»
»
»
»
»
»
»
¼
º
«
«
«
«
«
«
«
«
¬
ª
°
°
°
¿
°
°
°
¾
½
°
°
°
¯
°
°
°
®
c
c
c
cccccc
cccccc
cccccc
ccc
ccc
ccc
z
y
x
zxzzyxyzxxxz
zyzzyyyzxzxy
zyzxyyyxxyxx
zzyzxz
zyyyxy
zxyxxx
xz
yz
xy
z
y
x
S
S
S
llllll
llllll
llllll
lll
lll
lll
S
S
S
S
S
S
222
222
222
(6.34)
where,
»
»
»
¼
º
«
«
«
¬
ª
°
¿
°
¾
½
°
¯
°
®
ccc
ccc
ccc
zzxzx
xx
zxxzx
zzxzxz
zyyyxy
zxyxxx
lll
lll
lll
MMMMM
MM
MMMMM
cossinsinsincos
0cossin
sincossincoscos
(6.35)
S
x
c
, S
y
c
, and S
z
c
are the far-field stresses; S
x
, S
y
, S
z
,S
xy
, S
yz
and S
zx
are the
local borehole coordinate stresses;
M
x
is the angle between the global and
local coordinates (Fig. 6.2); and
M
z
is the borehole deviation.
After the conversion, the finite element analysis can be worked out in
the local coordinate system, i.e., the section perpendicular to the borehole
axial direction (Fig. 6.3).
X
Y
Z
X'
Y'
Z'
M
z
M
x
S
z´
S
x
´
S
y´
P
0
Fig. 6.2. Local and global coordinate systems for an inclined borehole.
6.4 Model validation 139
0
0.2
0.4
0.6
0.8
1
-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1
x(m)
y(m)
S
yx
S
xy
S
zx
S
xz
S
x
S
x
S
xy
0
0.2
0.4
0.6
0.8
1
-1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1
x(m)
y(m)
S
yx
S
xy
S
zx
S
xz
S
x
S
x
S
xy
S
yx
S
xy
S
zx
S
xz
S
x
S
x
S
xy
s
y
Fig. 6.3. Finite element mesh in the local coordinate system.
6.4 Model validation
The formulations presented in the foregoing section are coded in the
pseudo-three-dimensional and time domain using four-node rectangular
elements. Some analytical problems, such as elastic and poroelastic ana-
lytical solutions for inclined borehole problems, have been examined to
validate the computer program.
The geometric loading for an inclined borehole problem is depicted in
Fig. 6.2. The Cartesian coordinate system (xcyczc) is chosen to coincide
with the principal axes of the in-situ compressive stresses, respectively,
designated as S
x
, S
y
and S
z
. The initial formation pore pressure is denoted
by p
0
. The local coordinate system (Fig. 6.2) is formed by a rotation of the
azimuth angle,
M
x
, about the xc-axis, and then by an inclination of the
zenith angle,
M
z
, from the zc-axis toward the z-axis.
Then, at the local coordinate system the boundary conditions at the far-
field (
fo
r
) are characterized by the normal stresses:
zzyyxx
SSS
000
,,
VVV
and the shear stresses:
xzxzyzyzxyxy
SSS
000
,,
WWW

140 6 Double porosity poroelasticity and its finite element solution
as well as the matrix and fracture pore pressures at the far-field:
00
,
frfrmama
pppp
where the superscript ‘0’ indicates the virgin state.
In the following analysis, the in-situ stresses and initial pore pressures
are obtained from Woodland (1990) and Cui et al. (1997a): S
xc
= 29 MPa,
S
yc
= 20 MPa, S
zc
= 25 MPa, and p
0
= p
ma
0
= p
fr
0
= 10 MPa. The wellbore
inclination is
M
x
= 0q and
M
z
= 70q. The wellbore radius is R = 0.1 m. The
load at the wellbore is assumed as being applied instantaneously. In the lo-
cal coordinate system (after 70
q
inclination), these values become (Zhang
and Roegiers 2002, Zhang et al. 2003): S
x
= 25.5 MPa, S
y
= 20 MPa, S
z
=
28.5 MPa, S
xz
= 1.3 MPa, S
xy
= S
yz
= 0 MPa, and p
0
= p
ma
0
= p
fr
0
= 10 MPa,
as shown in Fig. 6.4. The formation materials are assumed to be isotropic,
characterized by the following properties: Biot modulus, M =15.8 GPa;
Biot's effective stress coefficient,
D
ma
= 0.771 and
D
fr
= 0.91; permeability,
k
ma
=
7
101
u
Darcy; and fluid dynamic viscosity, P = 0.001 Pas. The ana-
lytical solution for this particular generalized plane strain poroelastic prob-
lem was provided by Cui et al. (1997a). The corresponding equivalent pa-
rameters for the dual-porosity poroelastic model are listed in Table 6.1, in
which the selection of an exceptionally large fracture spacing, s, denotes
the approximation of a homogeneous single-porosity medium.
Table 6.1. Parameters for inclined borehole analysis
Parameter Unit Magnitude
Elastic modulus (E) GPa 20.6
Poisson’s ratio (Q)
- 0.189
Fracture stiffness (K
n
, K
sh
) MPa/m
4.821u10
5
Fluid bulk modulus (K
f
) MPa 419.17
Grain bulk modulus (K
s
) GPa 48.21
Matrix porosity (n
ma
) - 0.02
Fracture porosity (n
fr
) - 0.002
Matrix mobility (k
ma
/P)
m
2
/MPa·s 10
-10
Fracture mobility (k
fr
/P)
m
2
/MPa·s 10
-9
Fracture spacing (s)* m 10
7
* The use of extremely large fracture spacing is only for the validation with the
single porosity method.

6.4 Model validation 141
V
x
V
y
V
x
= 25.5 MPa
V
y
= 20.0 MPa
V
z
= 28.5 MPa
W
xz
= 1.3 MPa
pº
ma
= pº
fr
=10 MPa
p
ma
p
fr
T
Original conditions
(far-field stresses):
S´
x
= 29 MPa
S´
y
= 20 MPa
S´
z
= 25 MPa
pº
ma
=
p
º
fr
=10 MPa
Fig. 6.4. State of stress in the borehole local coordinate (the FEM section) for 70q
of borehole inclination.
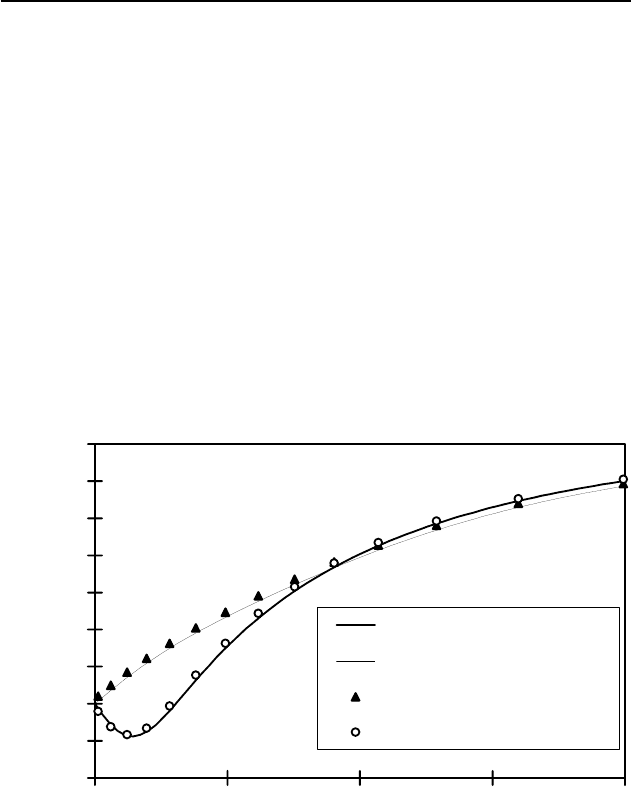
Figure 6.5 represents the pore pressure variations into the rock forma-
tion. The comparative results between the analytical solution and the
numerical dual-porosity solution (for large s) along the radial direction
T
=
5.7q are shown at two different times; the numerical results appear to agree
well with the analytical solution. It should be noted that the angle of
T
is
defined in Fig. 6.4.
0
2
4
6
8
10
12
1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 3
Dimensionless radial distance (r/R)
Pore pressure (MPa)
FEM,t=1.3min
FEM,t=21.6min
Analy.t=1.3min
Analy.t=21.6min
q 7.5
T
Fig. 6.5. Comparison between the finite element and analytical solutions for pore
pressure (
T
= 5.7q).
142 6 Double porosity poroelasticity and its finite element solution
For the same data set, the Terzaghi's effective radial stresses, defined as
the difference between the total radial stress and the pore pressure, are
plotted in Fig. 6.6 for
T
= 5.7q. Except for a slight difference in the near-
wellbore region, the analytical and finite element solutions match well.
The tensile region developed at early time is due to the non-monotonic
pore pressure distribution, which is consistent with the case reported by
Cui et al. (1997b).
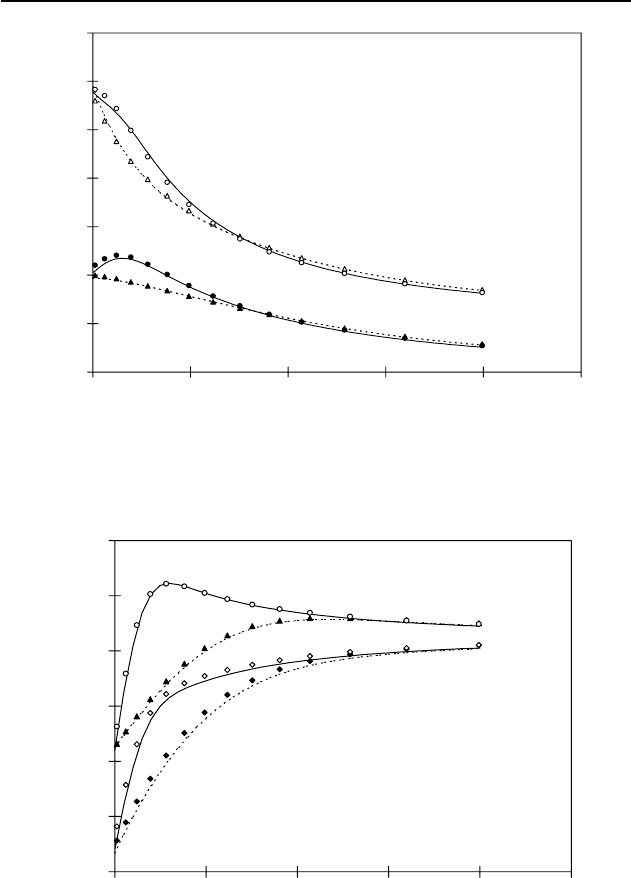
Figure 6.7 presents the total tangential stresses for two different radial
directions (
T
= 5.7 and 84.4q) and two different times (t = 1.3 and 21.6
min), and excellent agreement can be seen between the finite element and
analytical solutions for a larger time (t = 21.6 min). The small differences
in the near wellbore region at a small time are induced by initial condi-
tions, time step and boundary effects.
Also, good matches (refer to Fig. 6.8) are obtained for the total axial
stresses for two different radial directions (
T
= 0 and 90q) and two differ-
ent times (t = 1.3 and 21.6 min).
-4
-2
0
2
4
6
8
10
12
14
11.522.53
Dimensionless radial distance (r/R)
Effective radial stress (MPa)
Analy. solution, t=1.3 min
Analy. solution, t=21.6 min
Dual porosity, t=21.6 min
Dual porosity, t=1.3 min
q 7.5
T
Fig. 6.6. Comparison between the finite element and analytical solutions for
Terzaghi's effective radial stress (
T
= 5.7q).
6.4 Model validation 143
20
25
30
35
40
45
50
55
11.522.533.5
Dimensionless radial distance (r/R)
Total tangential stress (MPa)
T
q84 4.
T
q57.
Lines represent analytical solutions
Points represent FEM solutions
t=1.3 min for solid lines
t=21.6 min for dot lines
Fig. 6.7. Comparison between the finite element and analytical solutions for total
tangential stress along different radial sections (
T
= 5.7q,
T
= 84.4q) and times (t =
1.3 min, t = 21.6 min).
20
22
24
26
28
30
32
1 1.5 2 2.5 3 3.5
Dimensionless radial distance (r/R)
Total axial stress (MPa)
T
q90
T
q0
Lines represent analytical solutions
Points represent FEM solutions
t=1.3 min for solid lines
t=21.6 min for dot lines
Fig. 6.8. Comparison between the finite element and analytical solutions for total
axial stress along different radial sections (
T
= 0q,
T
= 90q) and times (t = 1.3 min,
t = 21.6 min).

144 6 Double porosity poroelasticity and its finite element solution
For the impermeable case, the double porosity finite element model with
extremely large fracture spacing and zero pore and fracture pressures
presents the approximation to the elastic solution (analytical solution in
Bradley 1979). The parameters used for the finite element model are the
same as in the previous calculation except that a mud pressure (p
w
= 10
MPa) is applied along the borehole wall. Along the radial section (
T
=
30q), the numerical and analytical solutions for radial and tangential
stresses are compared in Fig. 6.9. It shows that the proposed finite element
solutions return an excellent match with the analytical solutions except for
small discrepancies near the borehole wall.
0
5
10
15
20
25
30
35
1 1.5 2 2.5 3
Radial distance (r/R)
Total stress (MPa)
FEM, tangential
FEM, radial
Elastic, tangential
Elastic, radial
q 30
T
Fig. 6.9. Comparison between the finite element and analytical solutions for total
radial and tangential stresses along the radial sections (
T
= 30q) for the imperme-
able model.
6.5 Parametric analyses and application for borehole
stability
In this section, examples are given to demonstrate how certain parameters
in a double porosity medium affect the pore pressure and stress results.
The in-situ stresses, initial pore pressures, geometry and material proper-
ties used in the ongoing analyses are identical to those listed Table 6.1,
except for the fracture spacing s = 0.1 m. All the results are presented at a
borehole inclination angle of
M
z
= 70q. Figure 6.4 shows the far-field and
