Pelliccione M., Lu T.-M. Evolution of Thin Film Morphology: Modeling and Simulations
Подождите немного. Документ загружается.


A.4 Power Spectral Density Functions 161
»
( »)/
2
»
2
10
-1
10
0
10
1
10
3
10
-12
10
-8
10
-4
10
0
® = 1.00
® = 0.75
® = 0.50
® = 0.25
10
2
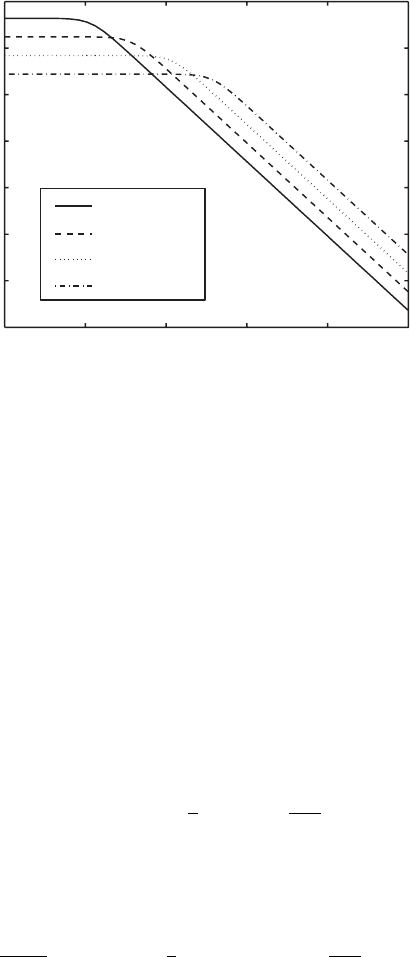
Fig. A.4. Sample self-affine PSD profiles on a log–log scale from (A.68) for different
values of α, including graphs with α =1.00, 0.75, 0.50, and 0.25. The behavior of
the PSD for large k is given by P (k) ∝ k
−2−2α
.
I =
ξ
√
2α
α+2
2
α
Γ(α +1)
1+
k
2
ξ
2
2α
1+α
.
Therefore, the Hankel transform of the autocorrelation function given in
(A.63) is
H
α
2
α−1
Γ(α +1)
r
ξ
√
2α
α
K
α
r
ξ
√
2α
=
ξ
2
1+
k
2
ξ
2
2α
1+α
. (A.67)
The PSD is w
2
/(2π) times the Hankel transform of the autocorrelation func-
tion from (2.22), which gives
P (k)=
w
2
ξ
2
2π
1+
k
2
ξ
2
2α
1+α
. (A.68)
The full width at half maximum (FWHM) of this PSD is given by
FWHM =
2α(2
1/(1+α)
− 1)
ξ
. (A.69)
162 A Mathematical Appendix
()/
2
10
-4
10
-2
10
0
10
4
10
-25
10
-15
10
-5
10
5
10
2
» = 100
» = 10
» = 1
» = 0.1
10
6
Fig. A.5. Sample self-affine PSD profiles on a log–log scale with different values for
ξ from (A.68). Larger values of the correlation length ξ result in a smaller full width
at half maximum (FWHM) as predicted by (A.69). All graphs have α =1.
For smaller values of the correlation length ξ, the PSD has a larger spread in
frequency space, as seen in Fig. A.5. In addition, the behavior of the PSD for
various values of α is shown in Fig. A.3, and on a log–log scale in Fig. A.4.
The behavior of the PSD for large k is given by P(k) ∝ k
−2−2α
, and thus the
slope of the PSD on a log–log scale for large k will be equal to −2 − 2α.
A.4.3 Mounded Surface – Exponential Model
The autocorrelation function for a mounded surface in 2+1 dimensions under
the exponential model is
R(r)=exp
−
r
ξ
2α
J
0
2πr
λ
. (A.70)
Because this autocorrelation function is the product of two functions, the PSD
is proportional to the convolution of the two Hankel transforms from (A.53),
P (k)=
w
2
(2π)
2
H
+
exp
−
r
ξ
2α
,
∗H
J
0
2πr
λ
. (A.71)
The Hankel transform of the Bessel function is given by (A.5),
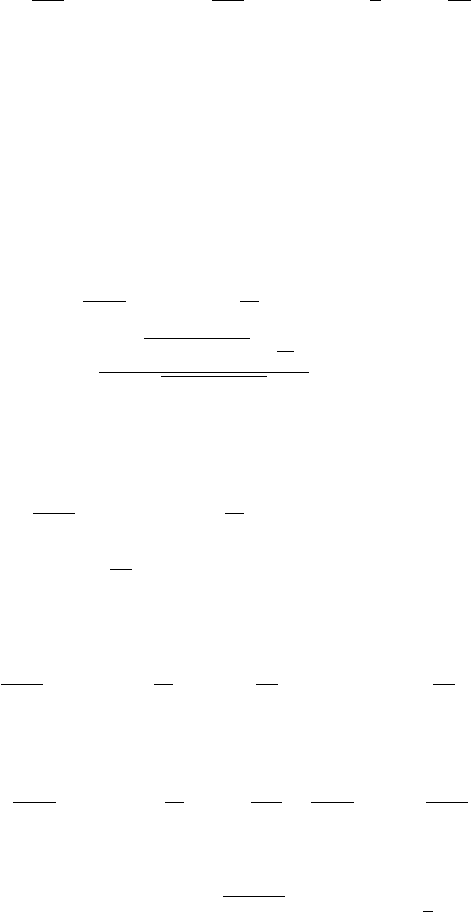
A.4 Power Spectral Density Functions 163
H
J
0
2πr
λ
=
∞
0
rJ
0
2πr
λ
J
0
(kr)dr =
1
k
δ
k −
2π
λ
. (A.72)
This relation is why the Bessel function is introduced in the autocorrelation
function in (A.70) because the convolution integral in (A.71) is much simpler
if one of the transforms is a delta function.
The Hankel transform of the exponential is more difficult, and we examine
the case where α = 1. The Hankel transform of the exponential when α =1
was found in Sect. A.4.1, and utilized in (A.60). The PSD is then given by
the convolution of the two Hankel transforms. We must take care to take the
convolution in Cartesian coordinates and then convert to polar to carry out
the integral.
P (k)=
w
2
ξ
2
8π
2
exp
−
ξ
2
4
(k
x
− x
)
2
+(k
y
− y
)
2
×
δ
(x
)
2
+(y
)
2
−
2π
λ
(x
)
2
+(y
)
2
dx
dy
.
Changing variables from Cartesian coordinates (x
,y
) to polar coordinates
(r, θ), dx
dy
= rdrdθ,gives
P (k)=
w
2
ξ
2
8π
2
2π
0
∞
0
exp
−
ξ
2
4
(k
x
− r cos θ)
2
+(k
y
− r sin θ)
2
×δ
r −
2π
λ
drdθ.
Integrating over the delta function,
P (k)=
w
2
ξ
2
8π
2
2π
0
exp
−
ξ
2
4
k
x
−
2π
λ
cos θ
2
+
k
y
−
2π
λ
sin θ
2
dθ.
Expanding the argument of the exponential gives
P (k)=
w
2
ξ
2
8π
2
2π
0
exp
−
ξ
2
4
k
2
+
4π
2
λ
2
−
4πk
x
λ
cos θ −
4πk
y
λ
sin θ
dθ.
This can be simplified with the relation
a cos θ + b sin θ =
a
2
+ b
2
cos
θ − tan
−1
b
a
,
which follows from the expansion of cos(x + y)=cosx cos y − sin x sin y.
Because the integral over θ is over a complete period of cos θ, the phase shift
of tan
−1
b/a does not affect the integral,

164 A Mathematical Appendix
P (k)=
w
2
ξ
2
8π
2
2π
0
exp
−
ξ
2
4
k
2
+
4π
2
λ
2
−
4πk
λ
cos θ
dθ
=
w
2
ξ
2
8π
2
exp
−
ξ
2
4
k
2
+
4π
2
λ
2
2π
0
exp
πkξ
2
λ
cos θ
dθ.
From (A.11), this can be written as
P (k)=
w
2
ξ
2
4π
exp
−
4π
2
+ k
2
λ
2
ξ
2
4λ
2
I
0
πkξ
2
λ
. (A.73)
This functional form assumes that α =1.Forα = 1, the Hankel transform of
the exponential in the autocorrelation function can be expressed as a series
from (A.58),
H
+
exp
−
r
ξ
2α
,
=
ξ
2
2α
∞
j=0
Γ
j+1
α
(j!)
2
−
k
2
ξ
2
4
j
. (A.74)
There is clearly a problem when α = 0, and this is addressed in the next
section. Carrying out similar steps to the calculation with α =1,thePSDfor
general α can be expressed as a series,
P (k)=
w
2
ξ
2
8π
2
α
∞
j=0
Γ
j+1
α
(j!)
2
−
πkξ
2
aλ
j
2π
0
[1 − a cos θ]
j
dθ, (A.75)
where a =4πλk/
k
2
λ
2
+4π
2
. This formula can be used for a numerical
computation of the PSD for various values of α. We forgo further analysis
of this form of the PSD because of the behavior for small α and introduce
another autocorrelation function that is valid as α → 0.
A.4.4 Mounded Surface – K -Correlation Model
Consider the autocorrelation function
R(r)=
α
2
α−1
Γ(α +1)
r
ξ
√
2α
α
K
α
r
ξ
√
2α
J
0
2πr
λ
. (A.76)
This is a combination of the autocorrelation function from the K -correlation
model proposed for self-affine surfaces in Sect. A.4.2, along with the Bessel
function introduced to model mounded surfaces. The advantage of this auto-
correlation function is that we already know the Hankel transforms for both
parts,
H
α
2
α−1
Γ(α +1)
r
ξ
√
2α
α
K
α
r
ξ
√
2α
=
ξ
2
1+
k
2
ξ
2
2α
1+α
, (A.77)
H
J
0
2πr
λ
=
1
k
δ
k −
2π
λ
. (A.78)

A.4 Power Spectral Density Functions 165
There are two reasons to consider this model for the autocorrelation function
over the exponential model introduced in Sect. A.4.3. First, the exponential
model for a mounded PSD diverges as α → 0, and the K -correlation model
will remedy this behavior. Also, the functional form of the PSD for α =1from
the exponential model involves transcendental functions as given in (A.73),
and is hard to analyze. We show that this new autocorrelation function gives
a PSD that is a rational function for α = 1. This allows us to analytically
solve for the peak position k
m
and see that it is equal to 2πλ
−1
under certain
conditions.
The Hankel transforms are already known, thus we can write the PSD as
the convolution
P (k)=
w
2
4π
2
ξ
2
1+
ξ
2
2α
(k
x
− x
)
2
+(k
y
− y
)
2
1+α
×
δ
(x
)
2
+(y
)
2
−
2π
λ
(x
)
2
+(y
)
2
dx
dy
.
Transforming to polar coordinates gives
P (k)=
w
2
ξ
2
4π
2
2π
0
dθ
1+
ξ
2
2α
k
2
+
4π
2
λ
2
−
4πk
λ
cos θ
1+α
.
It follows that the PSD is given by
P (k)=
w
2
ξ
2
4π
2
1
1+
k
2
ξ
2
2α
+
2π
2
ξ
2
αλ
2
1+α
2π
0
dθ
[1 − a cos θ]
1+α
, (A.79)
where
a =
2πξ
2
k
αλ
1+
k
2
ξ
2
2α
+
2π
2
ξ
2
αλ
2
.
This mounded PSD is pictured in Fig. A.6 for various values of α,andon
a log–log scale in Fig. A.7. We first examine this equation with α =1,then
discuss the expression for general α.Forα = 1, we need to use the result
2π
0
dθ
(1 − a cos θ)
2
=
2π
(1 − a
2
)
3/2
, (A.80)
which can be found using complex variable techniques. The PSD becomes
P (k)=
w
2
ξ
2
2π
1+
k
2
ξ
2
2
+
2π
2
ξ
2
λ
2
2
1
1 −
2πξ
2
k
λ
1+
k
2
ξ
2
2
+
2π
2
ξ
2
λ
2
2
3/2
(A.81)
166 A Mathematical Appendix
()
02
0.01
0.02
0
46810
® = 1.00
® = 0.75
® = 0.50
® = 0.25
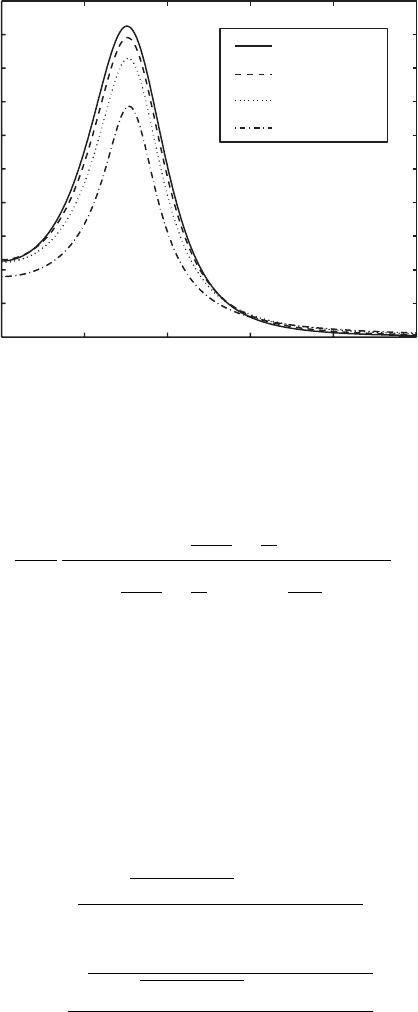
Fig. A.6. Sample mounded PSD profiles for different values of α from (A.79),
including graphs with α =1.00, 0.75, 0.50, and 0.25. All graphs have λ =2,ξ=1,
and w = 1. Note that the peak position lies at k
m
≈ π, which corresponds to 2π/λ.
=
w
2
ξ
2
2π
1+
2π
2
ξ
2
λ
2
+
ξ
2
2
k
2
1+
2π
2
ξ
2
λ
2
+
ξ
2
2
k
2
2
−
2πξ
2
λ
k
2
3/2
. (A.82)
This is the analytical form of the PSD for α = 1, and it is expressed as a
rational fraction. Now that we have an analytical PSD at our disposal, let us
investigate the relation k
m
=2πλ
−1
. To show this, we must set the derivative
of the PSD with respect to k equal to zero and solve for k
m
. Because the
PSD is a rational function, the derivative will also be a rational function, and
k
m
can be obtained by setting the numerator of the derivative equal to zero.
After some tedious algebra, one obtains
λ
4
ξ
4
k
4
m
+4λ
2
ξ
2
(π
2
ξ
2
+ λ
2
)k
2
m
− 4(2π
2
ξ
2
+ λ
2
)(4π
2
ξ
2
− λ
2
)=0.
This is a quadratic equation in k
2
m
, with solution
k
2
m
=
2πξ
4λ
2
+9π
2
ξ
2
− 2π
2
ξ
2
− 2λ
2
λ
2
ξ
2
.
We are only concerned with positive wavenumbers, so k
m
is given by
k
m
=
2πξ
4λ
2
+9π
2
ξ
2
− 2π
2
ξ
2
− 2λ
2
λξ
.
A.4 Power Spectral Density Functions 167
()
10
0
® = 1.00
® = 0.75
® = 0.50
® = 0.25
10
1
10
2
10
3
10
-12
10
-8
10
-4
10
0
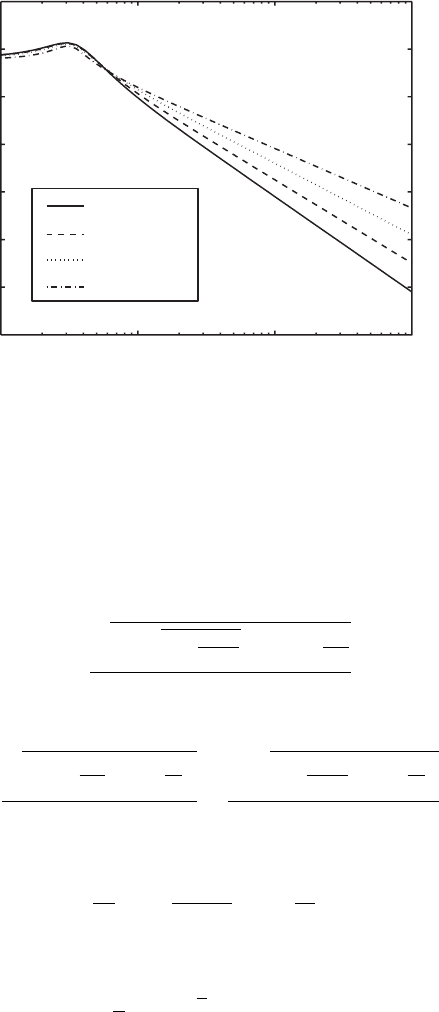
Fig. A.7. Sample mounded PSD profiles on a log–log scale for different values of
α from (A.79), including graphs with α =1.00, 0.75, 0.50, and 0.25. All graphs
have λ =2,ξ= 1, and w = 1. The behavior of the PSD for large k is given by
P (k) ∝ k
−2−2α
.
This is certainly more complicated than the simple relation k
m
=2πλ
−1
.
However, with a rearrangement we obtain
k
m
=
6π
2
1+
4λ
2
9π
2
ξ
2
− 2π
2
−
2λ
2
ξ
2
λ
.
We can Taylor expand the innermost square root to obtain
k
m
=
4π
2
−
2λ
2
3ξ
2
+ O
λ
4
ξ
4
λ
=
2π
1 −
λ
2
6π
2
ξ
2
+ O
λ
4
ξ
4
λ
.
Again Taylor expanding gives
k
m
=
2π
λ
1 −
λ
2
12π
2
ξ
2
+ O
λ
4
ξ
4
. (A.83)
This gives us a condition when k
m
≈ 2πλ
−1
,
λ
ξ
2π
√
3 ≈ 10.88. (A.84)

168 A Mathematical Appendix
Ordinarily, the wavelength is defined to be λ ≡ 2πk
−1
m
, and the last result
simply shows that (A.76) is consistent with this definition if the wavelength
is not an order of magnitude larger than the correlation length. A different
model for the autocorrelation function could give a better agreement with
the relation k
m
=2πλ
−1
, so there is room for improvement of this proposed
model.
The full width at half maximum (FWHM) of this PSD is more complicated
to determine, but in the regime where πξ
√
2 λ, the PSD is a function of kξ
only, which implies that FWHM ∝ ξ
−1
. Previous work has shown this behavior
to be true through a numerical analysis [187]. It is a reasonable conclusion
because the FWHM for a self-affine PSD is also inversely proportional to the
lateral correlation length, as was shown in (A.69).
For a general value of α, expanding the integrand in (A.79) and using
(A.43),
P (k)=
w
2
ξ
2
2πΓ(α +1)
1+
k
2
ξ
2
2α
+
2π
2
ξ
2
αλ
2
1+α
∞
j=0
Γ(2j + α +1)
(j!)
2
a
2
4
j
,
(A.85)
where
a =
2πξ
2
k
αλ
1+
k
2
ξ
2
2α
+
2π
2
ξ
2
αλ
2
.
This form does not diverge as α → 0 as can be seen from an appropriate
rearrangement of the PSD,
P (k)=
w
2
ξ
2
(2α)
1+α
2πΓ(α +1)
2α + k
2
ξ
2
+
4π
2
ξ
2
λ
2
1+α
∞
j=0
Γ(2j + α +1)
(j!)
2
a
2
4
j
,
(A.86)
where
a =
4πξ
2
λk
2αλ
2
+ k
2
ξ
2
λ
2
+4π
2
ξ
2
.
However, recall from Sect. A.4.2 that the behavior of the PSD when α =0
must be treated separately in terms of the cutoff frequency k
c
, which is not
discussed here. A plot of this form of the PSD for various values of α is
included in Fig. A.6. Changing the value of α does not significantly affect the
peak position or the width of the peak, although smaller values of α yield a
less pronounced peak intensity.
In the limit of large wavenumbers, k 2π/λ, a ≈ 4π/(kλ), and the sum
in (A.85) can be approximated by the first term. This gives
P (k 2π/λ) ≈
w
2
ξ
2
2π
1+
k
2
ξ
2
2α
1+α
, (A.87)

A.4 Power Spectral Density Functions 169
which is the form of a self-affine PSD from (A.68). This behavior is seen in
Fig. A.7, which is graphed on a log–log scale. On a logarithmic scale, the slope
of the graph for large k is −2 − 2α. Therefore, at wavenumbers much larger
than 2π/λ, or equivalently at length scales much smaller than λ, the surface
appears self-affine. Similarly, in the limit as λ →∞, a → 0; and the PSD
approaches the form of a self-affine PSD.
A.4.5 Summary
We present here a summary of the results for various forms of the power
spectral density function in 1+1 and 2+1 dimensions. The mathematics of
computing the PSD is similar in 1+1 dimensions to that presented in the
previous sections for 2+1 dimensions. In 1+1 dimensions, the PSD can be
expressed as
P (k)=
w
2
2π
∞
−∞
R(r)e
−ikr
dr
=
w
2
π
∞
0
R(r) cos krdr,
where the integration over the imaginary part of the exponential drops out
because the autocorrelation function R(r) is even. By expanding cos kr in
a Taylor series and integrating, the results for the PSD in 1+1 dimensions
can be obtained. Because the mathematics is very similar to the derivations
already presented, we simply summarize the results here. The only difference
in the autocorrelation functions in 1+1 dimensions and 2+1 dimensions is the
presence of a cos term in the mounded models instead of a Bessel function,
which allows for the analytical expressions that follow.
1+1 Dimensions
• Self-affine exponential model:
R(r)=exp
−
r
ξ
2α
, (A.88)
P (k)=
w
2
ξ
2πα
∞
j=0
Γ
j+1/2
α
(2j)!
−k
2
ξ
2
j
. (A.89)
• Self-affine exponential model (α =1):
R(r)=exp
−
r
ξ
2
, (A.90)
P (k)=
w
2
ξ
2
√
π
exp
−
k
2
ξ
2
4
. (A.91)
170 A Mathematical Appendix
• Self-affine K -correlation model:
R(r)=
α
2
α−1
Γ(α +1)
r
ξ
√
2α
α
K
α
r
ξ
√
2α
, (A.92)
P (k)=
w
2
ξ
√
2π
√
αΓ(α +1/2)
Γ(α +1)
1+
k
2
ξ
2
2α
−α−1/2
. (A.93)
• Mounded exponential model:
R(r)=exp
−
r
ξ
2α
cos
2πr
λ
, (A.94)
P (k)=
w
2
ξ
4πα
∞
j=0
Γ
j+1/2
α
(2j)!
−ξ
2
j
k −
2π
λ
2j
+
k +
2π
λ
2j
. (A.95)
• Mounded exponential model (α =1):
R(r)=exp
−
r
ξ
2
cos
2πr
λ
, (A.96)
P (k)=
w
2
ξ
2
√
π
exp
−
4π
2
+ k
2
λ
2
ξ
2
4λ
2
cosh
πkξ
2
λ
. (A.97)
• Mounded K -correlation model:
R(r)=
α
2
α−1
Γ(α +1)
r
ξ
√
2α
α
K
α
r
ξ
√
2α
cos
2πr
λ
, (A.98)
P (k)=
w
2
ξ
2
√
2π
√
αΓ(α +1/2)
Γ(α +1)
⎡
⎣
1+
k −
2π
λ
2
ξ
2
2α
−α−1/2
+
1+
k +
2π
λ
2
ξ
2
2α
−α−1/2
⎤
⎦
. (A.99)
