Печаткин А.В. Системы мобильной связи (часть 1) Принципы организации, функционирования и частотного планирования систем мобильной связи
Подождите немного. Документ загружается.

101
Такой же метод разнесения антенн используется и для обеспечения
связи в таких местах глубокой радиотени, как за большими промышлен-
ными зданиями, в ущельях, транспортных тоннелях, шахтах и т. д.
Применение одночастотных ретрансляторов позволяет обеспечить
непрерывность радиосвязи в сложных условиях города или пересеченной
местности без расширения частотного плана. Следует подчеркнуть, что
основным условием применимости ретрансляторов, принимающих и пере-
дающих на одной и той же частоте, является значительная развязка между
антеннами. В любом случае величина сигнала, принимаемого приемником
ретранслятора от базовой радиостанции, должна быть много больше, чем
величина сигнала на входе приемника, излученного самим ретранслято-
ром.
Соты для малонаселенных территорий имеют максимально боль-
шой радиус, приближающий их по характеристикам к транкинговой сети
связи. В случае, когда на такой территории может периодически появ-
ляться большое количество абонентов (как, например, в местах массового
отдыха), большая сота разделяется на несколько небольших виртуальных
сот. При этом не возникает проблем с нарушением частотного плана, по-
скольку в непосредственной близости не существует сот, базовые пе-
редатчики которых работают на совпадающих частотах.
Виртуальные соты закладываются в структуру сети связи на терри-
тории, где ожидаются большие пиковые нагрузки. В нормальной ситуации
эти соты не активны и не загружают выделенные линии связи и централь-
ный процессор. В момент загрузки, превышающей расчетную величину
(когда параметр GOS превышает допустимый), виртуальная сота активи-
руется. Центр мобильной коммутации распределяет на виртуальную соту
частотные каналы, не совпадающие с частотными каналами соседних сот.
Кроме того, на виртуальную соту могут быть частично перераспределены
частотные каналы соседних сот, работающих с меньшей загрузкой.
Вообще динамическое перераспределение рабочих каналов между со-
тами существенно повышает пропускную способность сети связи. При
жестком, фиксированном распределении рабочих частот между сотами
занятость всех рабочих каналов в соте приводит к отказу абоненту в уста-
новлении связи (с потерей вызова или постановкой в очередь). Если же
имеется возможность «занять» свободный канал в соседней соте, требуе-
мый сеанс связи может быть установлен. Разумеется, такое заимствование
возможно только с разрешения мобильного центра коммутации, который
контролирует частотный план в кластере и не допускает работы передат-
чиков соседних сот на совпадающих частотах [1,2].
102
4. ОЦЕНКА КАЧЕСТВА ОБСЛУЖИВАНИЯ В СИСТЕМЕ
При планировании телетрафика в пределах зоны обслуживания про-
водится предварительная оценка качества обслуживания абонентов. Под
качеством обслуживания понимается своевременное предоставление ка-
налов абонентам при обеспечении достоверности приема информации не
ниже заданной. Анализ работы систем мобильной связи показывает, что
только небольшая их часть одновременно пользуется услугами сети. При
этом интенсивность ее использования может изменяться во времени и
быть различной в зависимости от потребности индивидуальных абонен-
тов. Сеть обычно разрабатывается с учетом ожидаемой интенсивности ее
использования. Поэтому применяется транкинг, который означает, что
определенное количество каналов находится в распоряжении намного
большего количества пользователей [13].
Мобильные системы связи относятся к системам массового обслу-
живания, поскольку они представляют совокупность большого числа рав-
ноправных элементов. Процессы, протекающие в системах, также пред-
ставляют массу однородных случайных явлений и их закономерности оп-
ределяются не характеристиками отдельных элементов, а массовым ха-
рактером явлений в системе. Система телефонной связи исторически яв-
ляется первым примеров системы массового обслуживания; в частности, в
качестве первой математически корректной работы по теории массового
обслуживания называют работу датского ученого А. К. Эрланга «Теория
вероятностей и телефонные разговоры», опубликованную в 1909 г.
Модель процесса установления связи в мобильной системе может
быть описана следующим образом. Пусть на вход обслуживающего уст-
ройства, например, базовой станции, поступает поток вызовов от мобиль-
ных станций или телефонных аппаратов сети PSTN. Поток вызовов в сис-
теме имеет случайный характер, то есть каждый из вызовов может посту-
пить в любой случайный момент времени. Время обслуживания также
имеет случайный характер, из-за различной длительности разговоров. Ес-
ли в определенный момент времени число поступающих вызовов (заявок
на обслуживание) Z превышает число свободных каналов N на базовой
станции, то обслуживание будет задержано – «ожидание», или вообще со-
рвано – «отказ». Возникновение ситуаций «ожидания» или «отказ зависит
от обслуживающего устройства.
Обслуживающие устройства могут быть однофазовыми и многофазо-
выми. Примером однофазового обслуживающего устройства может слу-
103
жить пейджинговая система с централизованным диспетчированием, в ко-
торой контрольно-оконечная (базовая) станция обслуживается одним опе-
ратором (диспетчером). Диспетчер осуществляет прием данных по вызо-
вам из телефонной сети и их ввод в блок памяти для последующей пере-
дачи по каналу радиосвязи.
В многофазовых устройствах, например, в центральном коммутаторе
систем мобильной телефонной связи, один вызов обрабатывается не-
сколькими обслуживающими устройствами. Вызовы, поступающие на
любое обслуживающее устройство, могут обслуживаться в порядке оче-
реди, в случайном порядке, а также с преимуществом обслуживания (при-
оритеты). Если поступающие вызовы обслуживаются любой из свободных
коммутационных ячеек, то обслуживающее устройство является неупоря-
доченным.
Примером неупорядоченного обслуживающего устройства может
служить коммутационное поле электронной автоматической телефонной
станции (АТС). Если последующие вызовы обслуживаются иерархиче-
ской системой коммутационных ячеек, например, декадно-шаговые АТС,
то обслуживающее устройство является упорядоченным.
Основными параметрами оценки качества обслуживания мобильной
системы связи, как системы массового обслуживания, являются парамет-
ры входящего потока вызовов. Поскольку моменты поступления вызовов
в системе связи определяются периодичностью поступления информации,
являющейся случайной величиной, то весь процесс поступления вызовов
считается случайным процессом.
Случайными величинами такого потока вызовов являются:
количество вызовов, поступающих в единицу времени (интенсив-
ность вызовов или средняя частота поступления вызовов);
время обслуживания одного вызова T (средняя продолжительность
обслуживания вызова);
средний трафик A = T (интенсивность трафика, интенсивность
нагрузки, поток нагрузки), (эрл).
Для измерения показателей и T могут использоваться любые едини-
цы, однако во избежание путаницы удобно в обоих случаях использовать
одну и туже единицу времени – сутки, час, минуту, секунду.
В подавляющем большинстве случаев характеристики (параметры)
нагрузки – , T, A – обычно оценивают для часа пик, т. е. часового интер-
вала в период наибольшей нагрузки системы связи.

104
Параметры входящего потока вызовов могут иметь дискретный и не-
прерывный характер распределения. Характер распределения потока вы-
зовов будет дискретным, если случайной величиной является количество
вызовов . Характер распределения потока обслуживания вызовов будет
непрерывным, если случайной величиной является время обслуживания
вызова T.
Если случайный процесс является дискретным, то он характеризуется
свойствами стационарности, последействия и ординарности.
Стационарность дискретного потока вызовов означает, что для лю-
бой группы из числа различных отрезков времени вероятность поступле-
ния Z вызовов на протяжении каждого из отрезков времени обслуживания
t зависит только от значений Z и t и не изменяется при сдвиге всех вре-
менных отрезков на одну и ту же величину t, т. е. параметры потока не
зависят от времени.
Отсутствие последействия означает, что вероятность поступления Z
вызовов в течение отрезка времени t не зависит от того, сколько раз и как
поступали вызовы ранее (взаимная независимость появления количества
вызовов в различных отрезках времени).
Ординарность дискретного процесса вызовов является условием то-
го, что вероятность поступления двух или нескольких вызовов за сколь
угодно малый отрезок времени бесконечно мала, т. е. в один и тот же мо-
мент времени происходит только одно событие (один вызов).
Таким образом, если входящий дискретный поток вызовов в мобиль-
ной системе связи обладает стационарностью, отсутствием последействия
и ординарностью, то он является простейшим или пуассоновским. Для та-
кого потока, вероятность поступления Z вызовов за время t определяется
следующим образом [1,2,13]:
t
Z
e
!
Z
t
Z,tP
,
(4.1)
где – интенсивность потока вызовов (математическое ожидание числа
вызовов за единицу времени t).
Для пуассоновского потока вызовов выполняется условие равенства
математического ожидания и дисперсии σ процесса:
= D
= t.
(4.2)
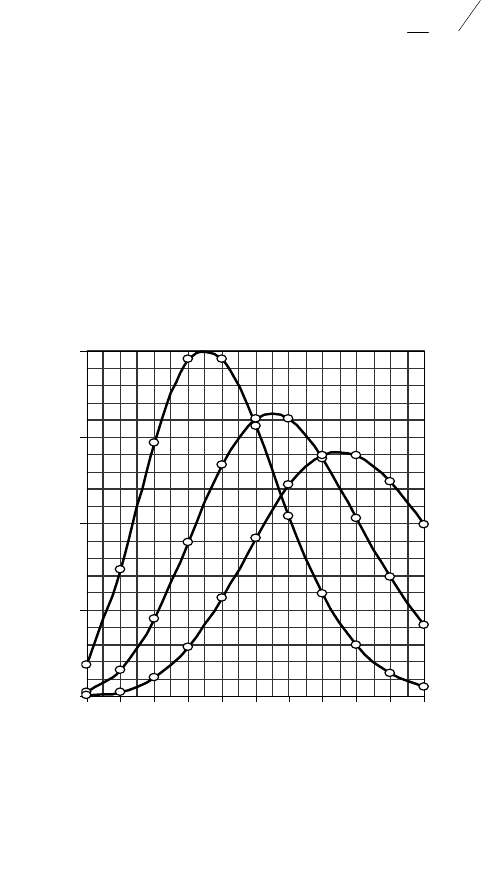
В качестве иллюстрации на рис. 4.1 приведены графики распределе-
ния Пуассона для:
105
= 20 выз/ч, T = 0,2 ч и t = 4 эрл;
= 30 выз/ч, T = 0,2 ч и t = 6 эрл;
= 40 выз/ч, T = 0,2 ч и t = 8 эрл;
Продолжительность обслуживания одного вызова (длительность за-
нятия одного канала связи), как уже отмечалось выше, представляет собой
непрерывную случайную величину, описываемую экспоненциальным
распределением,
T
e
T
W
1
, 0,
(4.3)
которому соответствует среднее значение и дисперсия
ср
= T; D
= T
2
,
(4.4)
т. е. среднее совпадает с определенной выше продолжительностью обслу-
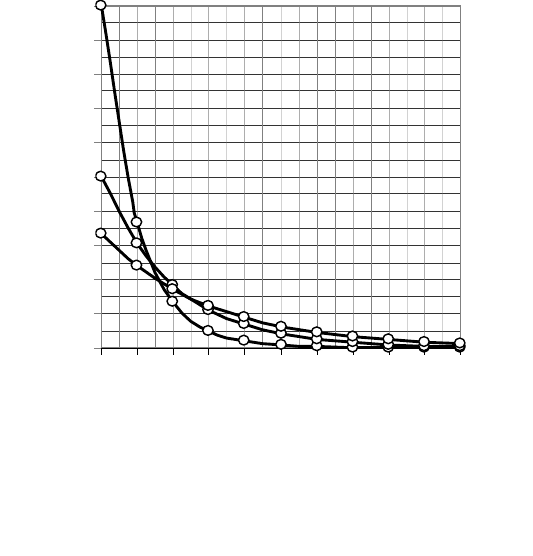
живания одного вызова. На рис. 4.2 приведен график экспоненциального
распределения для T
1
= 0,1 ч; T
2
= 0,2 ч; T
3
= 0,3 ч.
Вероятность поступления Z вы-
зовов P(t,z) в течение промежутка
времени t достигает наибольшего
значения при t = Z/, где Z = 0,1,2 и
т. д. Она может рассматриваться как
вероятность одновременного заня-
тия Z коммутационных ячеек, на-
пример, каналов базовой станции,
через которые проходят вызовы с
интенсивностью и средней про-
должительностью обслуживания ка-
ждого вызова t.
Выражение (6.1) определяет ве-
роятность поступления Z вызовов за
время t, равное средней продолжи-
тельности обслуживания одного вызова t
ср
.
Для определения вероятности P(t,Z) простейшего потока необходимо
только знание одного параметра – . Однако, простейший поток вызовов и
его закономерности справедливы только для однофазовых систем обслу-
живания. В многофазовых системах обслуживания наблюдаются орди-
нарные потоки вызовов с ограниченным последействием. В таких систе-
мах параметр D
.
.
Рис. 4.1. Распределение
Пуассона для различных
значений трафика
0,00
0,05
0,10
0,15
0,20
0 1 2 3 4 5 6 7 8 9 10
Число вызовов Z
Вероятность P(Z,t)
t=8
t=4
t=6
106
Рис. 4.2. Экспоненциальное распределение
при различных значениях T
T
1
=0,1
T
2
=0,2
T
3
=0
,3
0
1
2
3
4
5
6
7
8
9
10
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
Продолжительность обслуживания, ч
Плотность вероятности
Потоком вызовов с про-
стым последействием называ-
ется ординарный поток, для
которого в любой момент вре-
мени T отсутствует условный
параметр, зависящий только от
состояния системы обслужи-
вания в момент Т и от характе-
ристик вызова. Такой поток не
является стационарным.
Если параметр потока вы-
зовов с простым последейст-
вием зависит только от числа
вызовов Z, обслуживаемых в
данный момент, то такой поток
называется симметричным
потоком. В симметричном простейшем потоке вызовов параметр про-
порционален числу независимых и свободных в данный момент вызы-
вающих источников N.
Известны несколько моделей системы сотовой связи [1,2,13]:
1) модель Эрланга А; – система с ограничением времени ожидания и
времени обслуживания;
2) модель Эрланга B – система с отказами
3) модель Эрланга C – система с ожиданиями.
Во всех моделях поток вызовов принимается подчиняющимся рас-
пределению Пуассона, а продолжительность вызова – экспоненциальному
распределению. Разные модели отличаются между собой тем, как участь
постигает вызовы, поступившие в моменты времени, когда все каналы за-
няты. Эти вызовы могут аннулироваться (система с отказами – модель
Эрланга B); становиться в очередь и ждать освобождения канала неопре-
деленно долгое время (система с ожиданиями – модель Эрланга C) или
становиться в очередь и ждать освобождения канала ограниченное время
(система с очередностью обслуживания – модель Эрланга A).
Как уже отмечалось выше, количество вызовов является случайной
величиной, изменяющейся в зависимости от времени суток. Поэтому было
введено понятие часа наибольшей нагрузки (ЧНН) – часового временного
интервала, в котором трафик имеет максимальную интенсивность.

107
Уровень обслуживания (англ. Grade of Service – GOS) – это мера дос-
тупа к каналу в системе с концентрацией нагрузки в часы наибольшей на-
грузки (ЧНН). Во многих странах часы наибольшей нагрузки в сотовых
системах приходятся на часы пик с 16
00
до 18
00
по четвергам и пятницам
[1,2].
Уровень обслуживания (GOS) представляет собой качественную ме-
ру, используемую для определения вероятности получения доступа к ка-
налу при известном количестве каналов в сотовой системе.
Уровень обслуживания – один из основных параметров и критериев
оценки при разработке сотовых систем, который необходимо учитывать
для того, чтобы обеспечить требуемую емкость системы и распределение
каналов по сотам.
Уровень обслуживания обычно выражается в виде вероятности бло-
кировки (отказа), т. е. вероятности того, что желающий установить со-
единение пользователь столкнется с отсутствием свободного канала, или
что время ожидания свободного канала превысит установленный предел.
В общем виде функция Эрланга имеет вид:
0
P
!
N
t
)N(PGOS
N
,
(4.5)
где P(N) – вероятность отказа из-
за того, что все каналы заняты;
P
0
– вероятность того, что все каналы свободны.
4.1. СИСТЕМА С ОГРАНИЧЕНИЕМ ВРЕМЕНИ ОЖИДАНИЯ И
ВРЕМЕНИ ОБСЛУЖИВАНИЯ
В системе с ограничением времени ожидания и времени обслужива-
ния после ожидания (модель Эрланга А) вызов, поступивший в момент за-
нятости всех каналов, становиться в очередь, но время ожидания не пре-
вышает среднего времени обслуживания (средней продолжительности
разговора). Если за это время хотя бы один канал системы освобождается,
находящийся в очереди вызов занимает его на оставшуюся часть времени
обслуживания, после чего сбрасывается.
В такой системе вероятность отказа
NZ
A
AA
e
!Z
A
T,N,ZPGOS .
(4.6)

108
4.2. СИСТЕМА С ОТКАЗАМИ ИЛИ ПОТЕРЕЯННЫМИ
ВЫЗОВАМИ
В наиболее распространенной системе с отказами или потерянными
вызовами (модель Эрланга B) вероятность отказа в обслуживании, т. е. ве-
роятность того, что все каналы при поступлении вызова от абонента будут
заняты, определяется следующим выражением [13]:
N
Z
Z
N
N
Z
Z
N
BB
!Z
T
!N
T
!Z
A
!N
A
)T,N,Z(PGOS
0
0
.
(4.7)
Выражение (4.7) показывает, что отказы появляются, когда число од-
новременно поступающих вызовов Z будет превосходить количество ка-
налов N.
Вероятность того, что все каналы будут свободны
N
Z
Z
N
Z
Z
B
!Z
T
!Z
A
)T,N,Z(P
0
0
11
.
(4.8)
Вероятность того, что будут заняты K каналов
!
K
TP
!
K
AP
)T,N,Z(P
K
B
K
B
KB
00
.
(4.9)
Среднее число занятых каналов:
N
Z
Z
B
N
Z
Z
BB
!Z
T
P
!Z
A
P
1
0
1
0
11
.
(4.10)
4.3. СИСТЕМА С ОЖИДАНИЯМИ
Для системы с ожиданиями (модель Эрланга C) выражение для вы-
числения вероятности задержки обслуживания, т. е. вероятности поста-
новки в очередь, примет записывается следующим образом [13]:
1
0
1
0
N
Z
NZ
N
N
Z
NZ
N
СС
TN!N
T
!Z
T
)AN(!N
T
AN!N
A
!Z
A
)AN(!N
A
)T,N,Z(PGOS .
(4.11)
109
Вероятность того, что все каналы будут свободны
1
0
1
0
0
11
N
Z
NZ
N
Z
NZ
С
TN!N
T
!Z
T
AN!N
A
!Z
A
)T,N,Z(P .
(4.12)
Вероятность того, что будут заняты K каналов
!
K
TP
!
K
AP
)T,N,Z(P
K
C
K
C
KC
00
.
(4.13)
Среднее число занятых каналов:
N
Z
Z
C
N
Z
Z
CC
!Z
T
P
!Z
A
P
1
0
1
0
11
. (4.14)
Все рассмотренные выше аналитические выражения являются гро-
моздкими и крайне неудобными для непосредственного использования,
поэтому на практике применяют табулированные представления этих вы-
ражений. Пример такого табулированного эквивалента для моделей
Эрланга приведен в табл. 4.1.
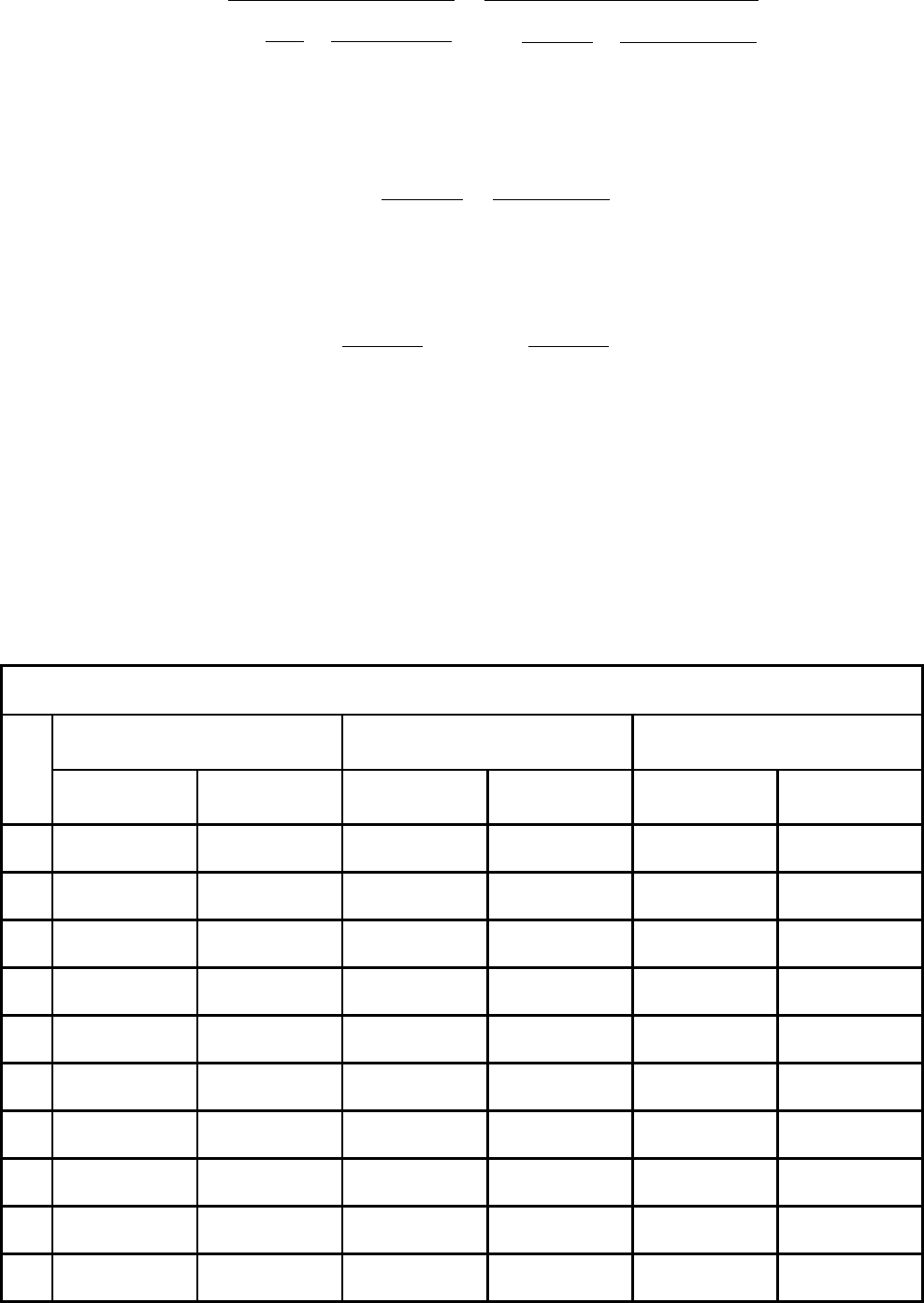
Таблица 4.1
Показатели качества обслуживания моделей Эрланга А и В
Вероятность отказа при заданном числе каналов базовой станции (GOS
B
, GOS
C
)
N = 8 N = 24 N = 32
Трафик
Модель B Модель C Модель B Модель C Модель B Модель C
1
9,12410
–6
1 ,30310
–6
0 ,000 0 ,000 0 ,000 0 ,000
3
8,132 10
–3
1 ,63710
–3
2,26610
–14
1 ,07910
–15
0 ,000 0 ,000
5 0 ,070 0 ,024
6,47310
–10
3 ,40710
–11
0 ,000 0 ,000
7 0 ,179 0 ,179
2 ,81610
–7
1 ,65610
–8
3,82710
–12
1 ,53110
–13
9 0 ,289 –0 ,686
1,58710
–5
1 ,05810
–6
1 ,61010
–9
7 ,00210
–11
11 0 ,383 –0 ,261
2 ,65210
–4
2 ,04010
–5
1 ,34010
–7
6 ,38210
–9
13 0 ,458 –0 ,204
1 ,98110
–3
1 ,80510
–4
3 ,80410
–6
2 ,00210
–7
15 0 ,519 –0 ,182
8 ,39410
–3
9 ,39610
–4
5 ,01610
–5
2 ,95110
–6
17 0 ,569 –0 ,172 0 ,024
3 ,44210
–3
3 ,72710
–4
2 ,48510
–5
19 0 ,609 –0 ,165 0 ,050 0 ,010
1 ,77510
–3
1 ,36810
–4
110
4.4. ОЦЕНКА ЕМКОСТИ СИСТЕМ СОТОВОЙ СВЯЗИ
При оценках емкости систем сотовой связи обычно используют мо-
дель системы с отказами (модель Эрланга B), в то время как модель сис-
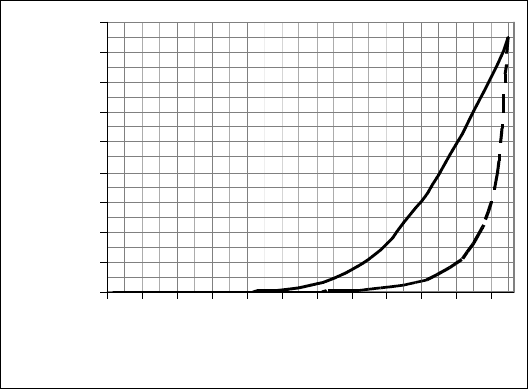
темы с ожиданием (модель Эрланга С) применяют гораздо реже. Как вид-
но из графиков на рис. 4.3, построенных для системы с количеством кана-
лов N = 64 и средним трафиком А = [0...63], при малых вероятностях отка-
за в обслуживании, т. е. при
малом трафике, обе модели
дают достаточно близкие ре-
зультаты. Однако при вероят-
ности отказа в обслуживании
P > 0,1 в системе с ожидания-
ми вероятность отказа будет
возрастать очень резко, что
свидетельствуют о сущест-
венном ухудшении качества
обслуживания. Поэтому на
практике при анализе емкости
системы связи расчеты прово-
дят для вероятностей в диапа-
зоне P = [0,01...0,05].
Анализируя вышеизложенное и опираясь на данные таблицы 4.1,
можно сделать следующий вывод: с увеличением числа каналов, выде-
ленных базовой станции, трафик, т. е. количество передаваемой информа-
ции, растет быстрее, чем число каналов, особенно при N < 30. Следова-
тельно, рациональное построение системы сотовой связи должно преду-
сматривать выделение на одну ячейку (базовую станцию) не менее 30 час-
тотных каналов (для систем, использующих временное разделение кана-
лов, не менее 30 физических каналов – временных слотов).
Рассмотрим пример использования системы с отказами (модель Эр-
ланга B). В ее состав входят три основных параметра: число каналов N,
трафик A и вероятность отказа P
В
. Если известны любые два параметра, то
можно однозначно определить третий [2].
Пример.
Условная городская агломерация занимает площадь S = 3300 км
2
и ох-
вачена системой сотовой связи.
В системе используются кластеры из семи сот N
кл
= 7.
Каждая сота имеет радиус r = 6 км.
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
29 32 35 38 41 44 47 50 53 56 59 62
Трафик А , эрланг
Вероятность отказа P
Рис. 4.3. Вероятность отказа
в обслуживании в зависимости от трафика
при числе каналов N=64
Модель с отказами
Модель с ожиданием
