Підручник - Алгебра і початок аналізу 10 клас Нелін Академічний рівень

Подождите немного. Документ загружается.

§ 12. Узагальнення поняття степеня. Степенева функція, її властивості та графік 191

()()

−+

−

abab

;



) 

−+

()

()()

+−+

−+

xxx

339

3.

b l 0, х l 0. Тоді в завданні 1 не-

від’ємні числа а і b можна подати

як квадрати:

aa=

()

bb=

()

і ви-

користати формулу різниці квад-

ратів: х

– у

= (х – у) (х + у), а в

завданні 2 подати невід’ємне чис-

ло х як куб: xx=

()

і використати

формулу розкладу суми кубів:

+ b

= (а + b) (а

– аb + b

Приклад 4 Розв’яжіть рівняння:

1= ; 2

)

1= .

Розв’язання Коментар

1)  x

1= . ОДЗ: х ∈ R,

= 1,

х = ±1.

Відповідь: ±1. 

)  x

1= . ОДЗ: х l 0,

= 1,

х = ±1.

Ураховуючи ОДЗ, одержуємо

х = 1.

Відповідь: 1. 

Область допустимих значень

рівняння

— усі дійсні чис-

ла, а рівняння x

1= — тільки

х l 0.

При піднесенні обох частин рів-

няння до куба одержуємо рівняння,

рівносильне заданому на його ОДЗ.

Отже, пер�ому рівнянню задоволь-

няють усі знайдені корені, а друго-

му — тільки невід’ємні.

(У завданні 1 також ураховано,

що

()

= , а в завданні 2 — що

xxx

(

)

Запитання для контролю

1. Дайте означення степеня з натуральним показником. Наведіть при-

клади обчислення таких степенів.

2. Дайте означення степеня з цілим від’ємним показником та з нульо-

вим показником. Наведіть приклади обчислення таких степенів.

При яких значеннях а існують значення виразів а

та а

–n

, де n ∈ N?

192 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ

Дайте означення степеня з раціональним показником

= , де

т — ціле число, а п — натуральне, не рівне 1. Наведіть приклади

обчислення таких степенів. При яких значеннях а існують значення

виразу

Укажіть область допустимих значень виразів a

і a

−

4. Запи�іть властивості степенів з раціональними показниками. На-

ведіть приклади використання цих властивостей.

. Обґрунтуйте властивості степенів з раціональними показниками.

. Поясніть на прикладі, як можна ввести поняття степеня з ірраціо-

нальним показником.

Вправи

1°. Подайте вираз у вигляді кореня з числа:

; 2) 3

−

; 3) 5

0,25

; 4)

−

;

5) 2

1,5

; 6) 7

−

2. Подайте вираз у вигляді степеня з раціональним показником:

1°)

;

2°) 4

; 3°) 7

9−

;

−2

при a > 0; 5)

при b l 0; 6

)

3°. Чи має зміст вираз:

−

()

;

2) (–5)

–2

; 3)

; 4) 0

–5

4. Знайдіть область допустимих значень виразу:

;

2) х

–3

; 3)

()

;x −

−

()

;x + 3

5) (х

– 1)

; 6) х

– 5.

5. Знайдіть значення числового виразу:

1) 243

0,4

; 2)













−

; 3) 16

; 4)

125













;

25 81 125

(

)

−

ææ

;

(

)

−

(

)

−

æææ ;

(

)

−

(

)













−

ææ

6. Розкладіть на множники:

()

;ax ay

+ 2) aa−

; 3) 33

+ ; 4) ab aab+++

§ 12. Узагальнення поняття степеня. Степенева функція, її властивості та графік 193

7. Скоротіть дріб:

−

; 2)

−

; 3)

−

;

−+

Спростіть вираз (8–9).

8. 1)

()

−

; 2) xy xy

2−

()

+ ;

3) xxx

111+

()

−

()

; 4) klklkl

()

−

()

9. 1)

−

; 2)

−

;

−

;

−+

10. Розв’яжіть рівняння:

1) x

1= ; 2) x

2= ; 3) x

2= ; 4)

2= .

194 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ

12.2. Степенева функція, її властивості та графік

Таблиця 21

Означення. Функція виду у = х

, де α — будь-яке дійсне число,

називається степеневою функцією.

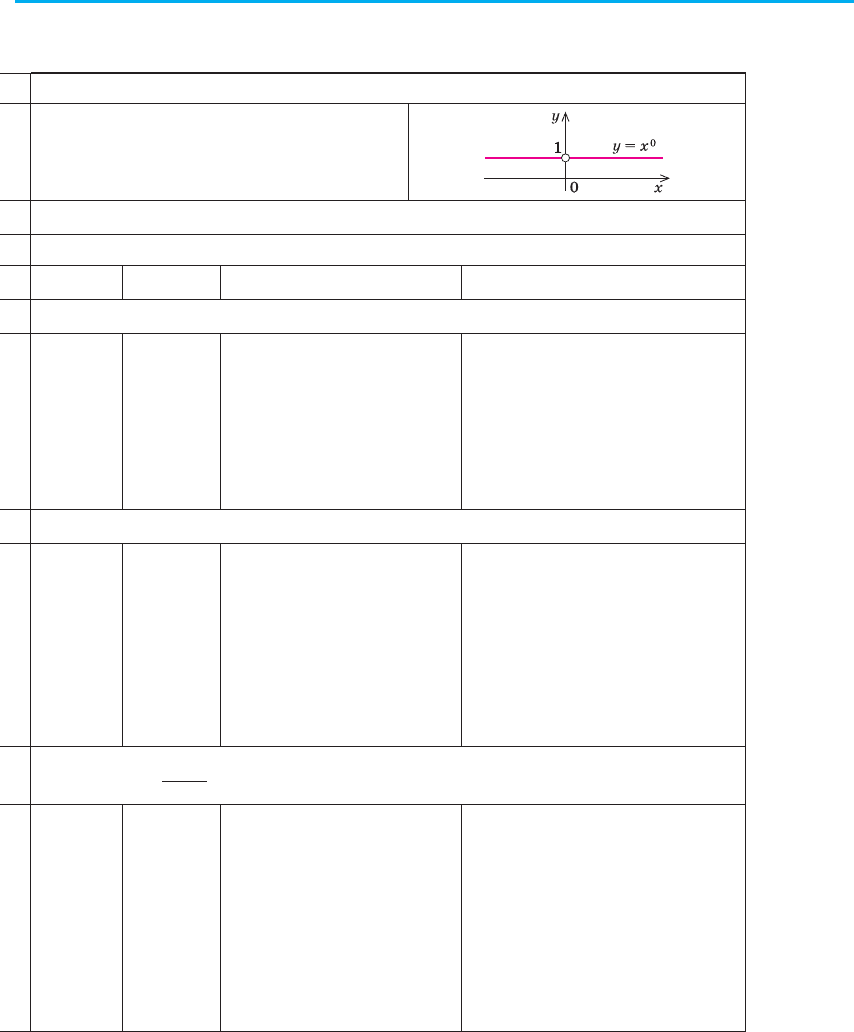
Особливий випадок (α = 0)

Якщо α = 0, то

y = x

= x

= 1 (при х ≠ 0).

Графіки і властивості

функції у = х

(при α ≠ 0)

Графік

Властивості

D (y) E (y)

парність і непарність зростання і спадання

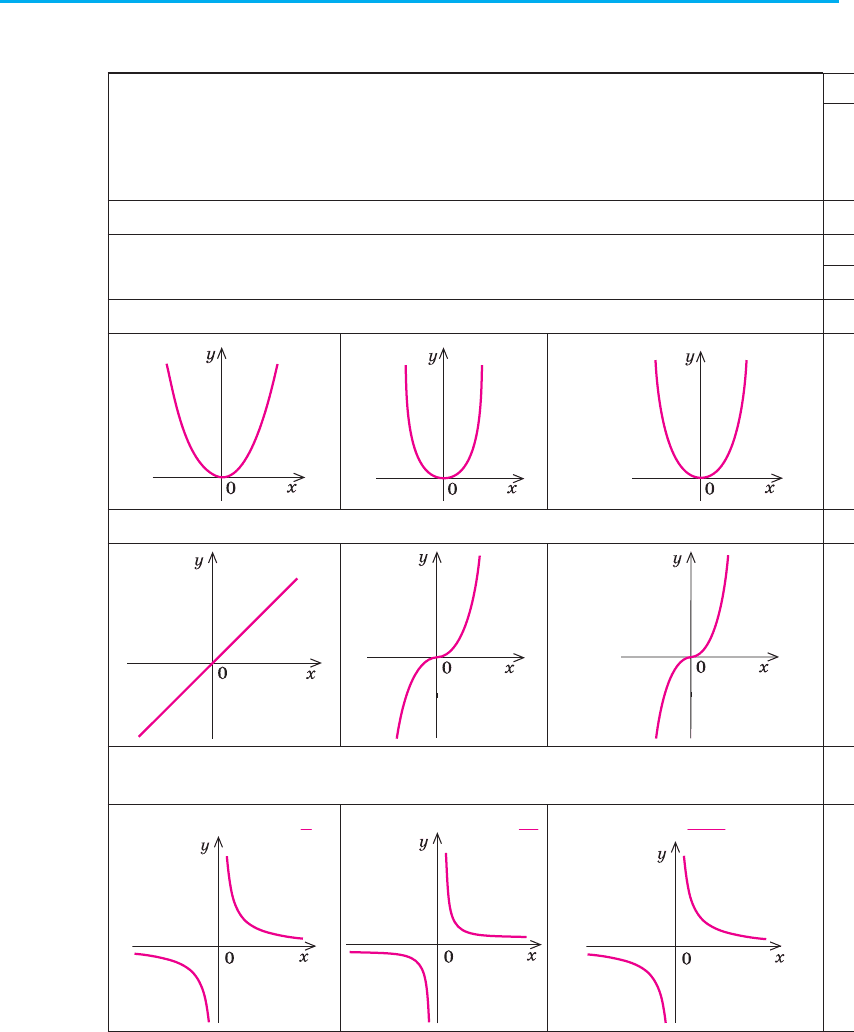
1. у = х

, α — парне натуральне число (y = x

, n ∈ N)

y = x

n ∈ N

[0; +∞) Парна

Спадає на проміжку

(–∞; 0], зрос тає

на про міжку [0; +∞)

2. у = х

, α — непарне натуральне число (у = х та у = х

2n + 1

, п ∈ N)

y = x

2n+1

n ∈ N

R R

Непарна Зростає

3. у = х

, α — непарне від’ємне число

()

yx n

== ∈

−−

−

()

yx n

−−

−

== ∈N

х ≠ 0 у ≠ 0

Непарна

Спадає на кожному

з проміжків (–∞; 0)

і (0; +∞)

§ 12. Узагальнення поняття степеня. Степенева функція, її властивості та графік 195

12.2. Степенева функція, її властивості та графік

Таблиця 21

Означення. Функція виду у = х

, де α — будь-яке дійсне число,

називається степеневою функцією.

Особливий випадок (α = 0)

Якщо α = 0, то

y = x

= x

= 1 (при х ≠ 0).

Графіки і властивості

функції у = х

(при α ≠ 0)

Графік

Властивості

D (y) E (y)

парність і непарність зростання і спадання

1. у = х

, α — парне натуральне число (y = x

, n ∈ N)

y = x

n ∈ N

[0; +∞) Парна

Спадає на проміжку

(–∞; 0], зрос тає

на про міжку [0; +∞)

2. у = х

, α — непарне натуральне число (у = х та у = х

2n + 1

, п ∈ N)

y = x

2n+1

n ∈ N

R R

Непарна Зростає

3. у = х

, α — непарне від’ємне число

()

yx n

== ∈

−−

−

()

yx n

−−

−

== ∈N

х ≠ 0 у ≠ 0

Непарна

Спадає на кожному

з проміжків (–∞; 0)

і (0; +∞)

196 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ

Продовження табл. 21

Графіки і властивості

функції у = х

(при α ≠ 0)

Графік

Властивості

D (y) E (y)

парність і непарність зростання і спадання

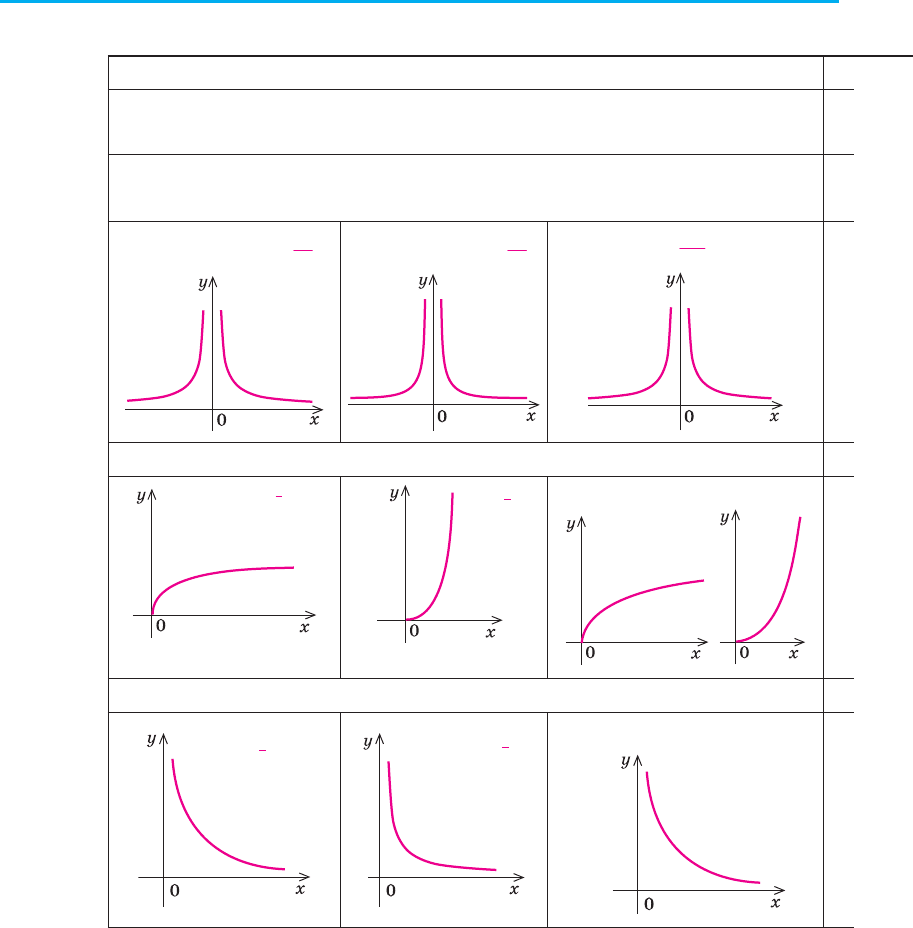
4. у = х

, α — парне від’ємне число

(,yx n

== ∈

−2

−

yx n

−

== ∈ N

х ≠ 0

(0; +∞) Парна

Зростає

на проміжку (–∞; 0),

спадає

на проміжку (0; +∞)

5. у = х

, α — неціле додатне число

yx=

ó = õ

(

> 0,

— íåöiëå)

α > 1

0< α < 1

[0; +∞) [0; +∞) Ні парна, ні непарна Зростає

6. у = х

, α — неціле від’ємне число

yx=

−

y = õ

(

< 0,

— íåöiëå)

(0; +∞) (0; +∞) Ні парна, ні непарна Спадає

§ 12. Узагальнення поняття степеня. Степенева функція, її властивості та графік 197

Продовження табл. 21

Графіки і властивості

функції у = х

(при α ≠ 0)

Графік

Властивості

D (y) E (y)

парність і непарність зростання і спадання

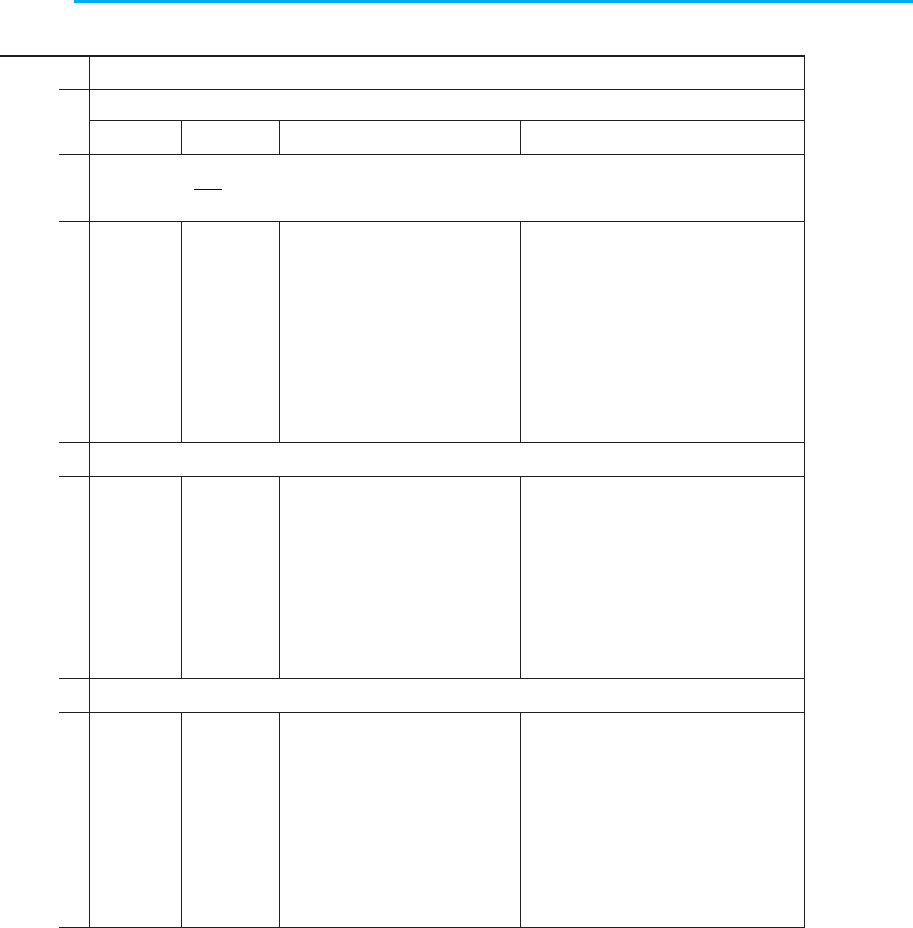
4. у = х

, α — парне від’ємне число

yx n

== ∈

−2

−

yx n

−

== ∈ N

х ≠ 0

(0; +∞) Парна

Зростає

на проміжку (–∞; 0),

спадає

на проміжку (0; +∞)

5. у = х

, α — неціле додатне число

yx=

ó = õ

(α > 0, α — íåöiëå)

α > 1

0< α < 1

[0; +∞) [0; +∞) Ні парна, ні непарна Зростає

6. у = х

, α — неціле від’ємне число

yx=

−

y = õ

(α < 0, α — íåöiëå)

(0; +∞) (0; +∞) Ні парна, ні непарна Спадає

198 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ

Пояснення й обґрунтування

Степеневими функціями називають функції виду у = х

, де α —

будь-яке дійсне число.

З окремими видами таких функцій ви вже ознайомилися в курсі

алгебри 7–9 класів. Це, наприклад, функції у = х

= х, у = х

, у = х

. При

довільному натуральному α графіки і властивості функції у = х

анало-

гічні відомим вам графікам і властивостям указаних функцій.

Описуючи властивості степеневих функцій, виділимо ті характерис-

тики функцій, які ми використовували в § 10: 1) область визначення;

2) область значень; 3) парність чи непарність; 4) точки перетину з осями

координат; 5) проміжки знакосталості; 6) проміжки зростання і спадан-

ня; 7) найбіль�е та наймен�е значення функції.

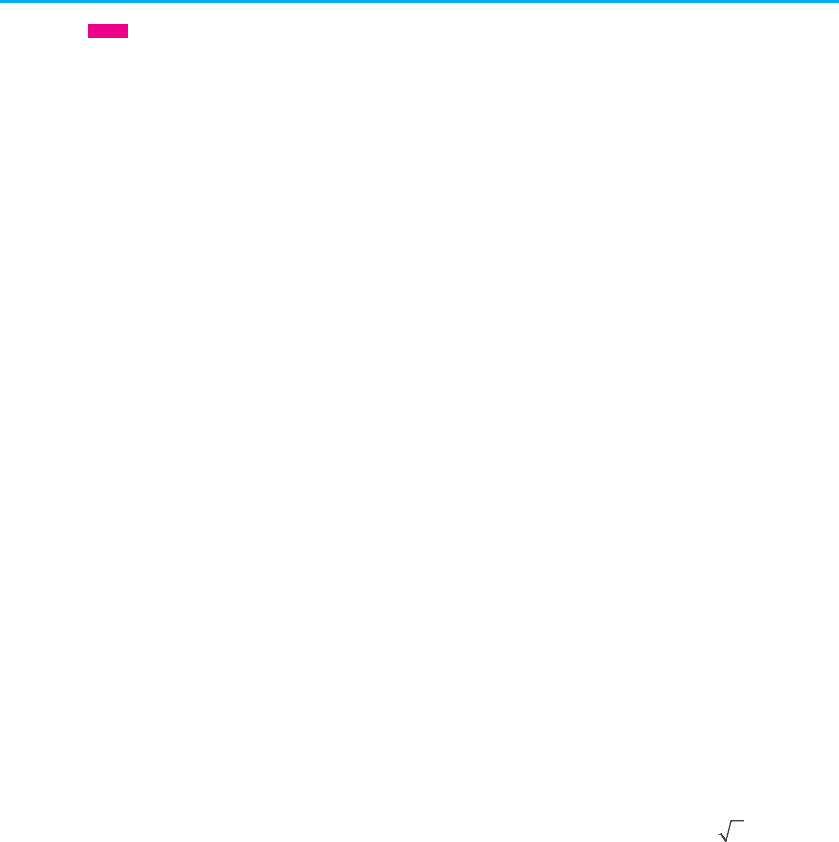
1. Функція y = x

(α — парне натуральне число). Якщо α — парне на-

туральне число, то функція у = х

, п ∈ N, має властивості та графік,

повністю аналогічні властивостям і графіку функції у = х

Дійсно, область визначення функції у = х

: D (y) = R, оскільки зна-

чення цієї функції можна обчислити при будь-яких значеннях х.

Функція парна: якщо f (х) = х

, то f (–х) = (–х)

= х

= f (х). Отже,

графік функції у = х

симетричний відносно осі Оу.

Оскільки при х = 0 значення у = 0, то графік функції y = x

завжди

проходить через початок координат.

На проміжку [0; +∞) функція зростає.

 Дійсно, для невід’ємних значень при x

> x

l 0, x

l 0) одержу-

ємо

> ,

оскільки, як відомо з курсу алгебри 9 класу, при під-

несенні обох частин правильної нерівності з невід’ємними членами

до парного степеня (із збереженням знака нерівності) одержуємо

правильну нерівність. 

На проміжку (–∞; 0] функція спадає.

 Дійсно, для недодатних значень x

і x

m 0, x

m 0), якщо x

> x

то –x

< –x

(і тепер –x

l 0, –x

l 0). Тоді (–x

)

< (–x

)

, отже,

< , тобто f (x

) < f (x

). 

Для того щоб знайти область значень функції у = х

, п ∈ N, складемо

рівняння x

= a. Воно має розв’язки для всіх а l 0 (тоді

=±

)

і тіль-

ки при таких значеннях а. Усі ці числа і складуть область значень функ-

ції. Отже, область значень заданої функції: у l 0, тобто Е (у) = [0; +∞).

Таким чином, для всіх дійсних значень x значення у l 0. Найменше

значення функції дорівнює нулю (y = 0 при x = 0). Найбільшого значен-

ня функція не має.

Зазначимо також, що при x = 1 значення y = 1

= 1.

Ураховуючи властивості функції у = х

, п ∈ N, одержуємо її графік

(рис. 85).

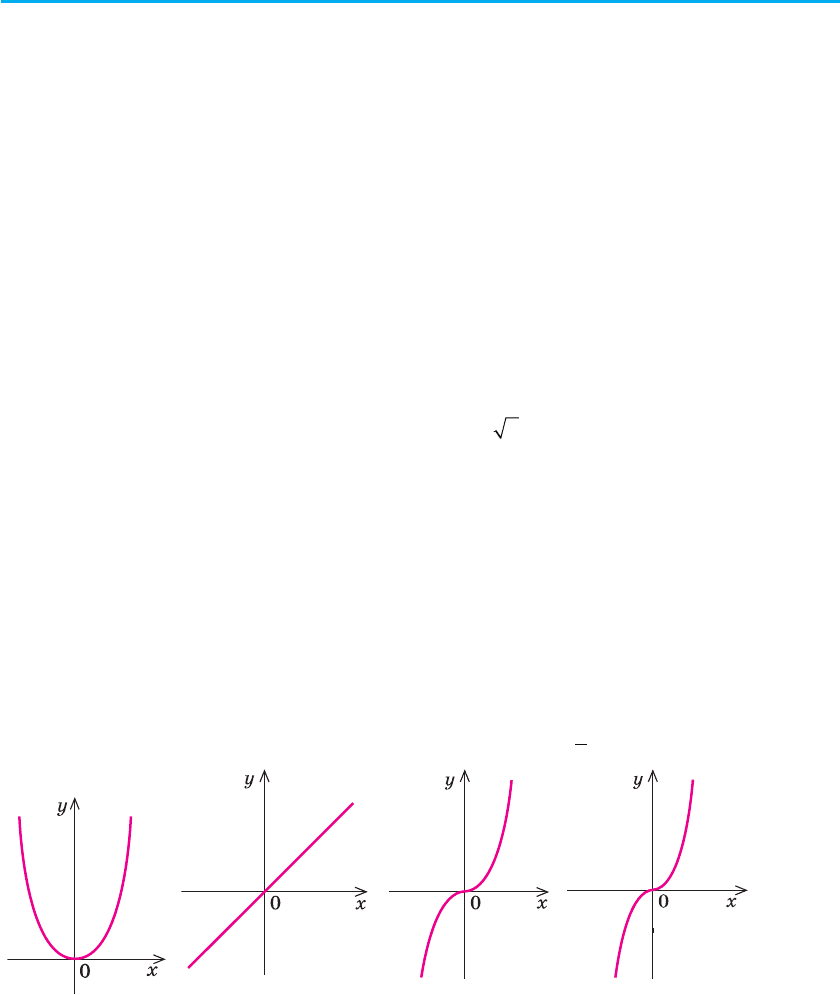
§ 12. Узагальнення поняття степеня. Степенева функція, її властивості та графік 199

2. Функція y = x

(α — непарне натуральне число). Якщо α — непарне

натуральне число (α = 2n – 1, n ∈ N), то властивості функції y = х

2n – 1

п ∈ N, аналогічні властивостям функції y = x

Дійсно, область визначення функції y = х

2n – 1

, п ∈ N: D (y) = R,

оскільки значення цієї функції можна обчислити при будь-яких зна-

ченнях х.

Функція непарна: якщо f (х) = х

2n – 1

, то f (–х) = (–х)

2n – 1

= –х

2n – 1

= –f (х). Отже, графік функції симетричний відносно початку координат.

Оскільки при х = 0 значення у = 0, то графік функції у = х

2n – 1

зав-

жди проходить через початок координат.

На всій області визначення функція зростає.

 Дійсно, при x

> x

одержуємо

21−−

> , оскільки при піднесенні

обох частин правильної нерівності до непарного степеня (із збере-

женням знака нерівності) одержуємо правильну нерівність. 

Для знаходження області значень функції у = х

2n – 1

, п ∈ N, складемо

рівняння х

2n – 1

= a. Воно має розв’язки для всіх a ∈ R (при n = 1 одержу-

ємо x = a, а при n ≠ 1, п ∈ N, одержуємо

)

−21

. Отже, область зна-

чень заданої функції: y ∈ R, тобто Е (у) = R = (–∞; +∞).

Тому найменшого і найбільшого значень функція не має.

Проміжки знакосталості: при x > 0 значення y = x

2n – 1

> 0,

при x < 0 значення y = x

2n – 1

< 0.

Зазначимо також, що при x = 1 значення y = 1

2n – 1

= 1.

Як відомо з курсу алгебри та геометрії, графіком функції y = x

= x

є пряма, якa проходить через початок координат (рис. 86), а при ін�их

непарних натуральних α функція y = x

2n + 1

, п ∈ N, має графік, аналогіч-

ний графіку функції у = х

(рис. 87).

3. Функція y = x

(α — непарне від’ємне число). Якщо α — непарне

від’ємне число, то функція y = x

–(2n – 1)

, п ∈ N, має властивості та графік,

повністю аналогічні властивостям і графіку функції y

y = x

n ∈ N

y = x

2n+1

n ∈ N

Рис. 85 Рис. 86 Рис. 87

200 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ

Дійсно, область визначення функції

−−

()

−

х ≠ 0, тобто

D (y) = (–∞; 0) È (0; +∞), оскільки значення цієї функції можна об-

числити при будь-яких значеннях х, крім x = 0.

Функція непарна: при х ≠ 0, якщо f (x) = x

–(2n – 1)

, то

f (–х) = (–х)

–(2n – 1)

= –х

–(2n – 1)

= –f (х).

Отже, графік функції симетричний відносно початку координат.

Ураховуючи, що х ≠ 0 і y ≠ 0 yx

==≠

()

−−

()

−

одержуємо, що

графік функції y = x

–(2n – 1)

не перетинає осі координат.

На проміжку (0; +∞) функція спадає.

 Дійсно, для додатних значень при x

> x

> 0, x

> 0) одержуємо

21−−

> , але тоді

nn−−

< , отже,

−− −−

() ()

.

На проміжку (–∞; 0) функція теж спадає. Це випливає з того, що її

графік симетричний відносно початку координат.

 Наведемо також і аналітичне обґрунтування: якщо x

< 0, x

< 0

і x

> x

, то –x

< –x

(і тепер –x

> 0, –x

> 0). Тоді за обґрунтова-

ним вище (–x

)

–(2n – 1)

> (–x

)

–(2n – 1)

, отже, −>−

−− −−

() ()

. Звідси

−− −−

() ()

.

Для того щоб знайти область значень функції y = x

–(2n – 1)

, п ∈ N,

складемо рівняння x

–(2n – 1)

= a, тобто

n−

= . Воно має розв’язки для

всіх а ≠ 0 (тоді x

−

при n ≠ 1 і x

при n = 1) і тільки при таких

значеннях а. Усі ці числа і складуть область значень функції. Отже, об-

ласть значень заданої функції: у ≠ 0, тобто Е (у) =(–∞; 0) È (0; +∞).

Тому найменшого і найбільшого значень функція не має.

Проміжки знакосталості:

при x > 0 значення y = x

–(2n – 1)

> 0,

а при x < 0 значення

y = x

–(2n – 1)

< 0.

Зазначимо також, що при x = 1

значення y = 1

–(2n – 1)

= 1.

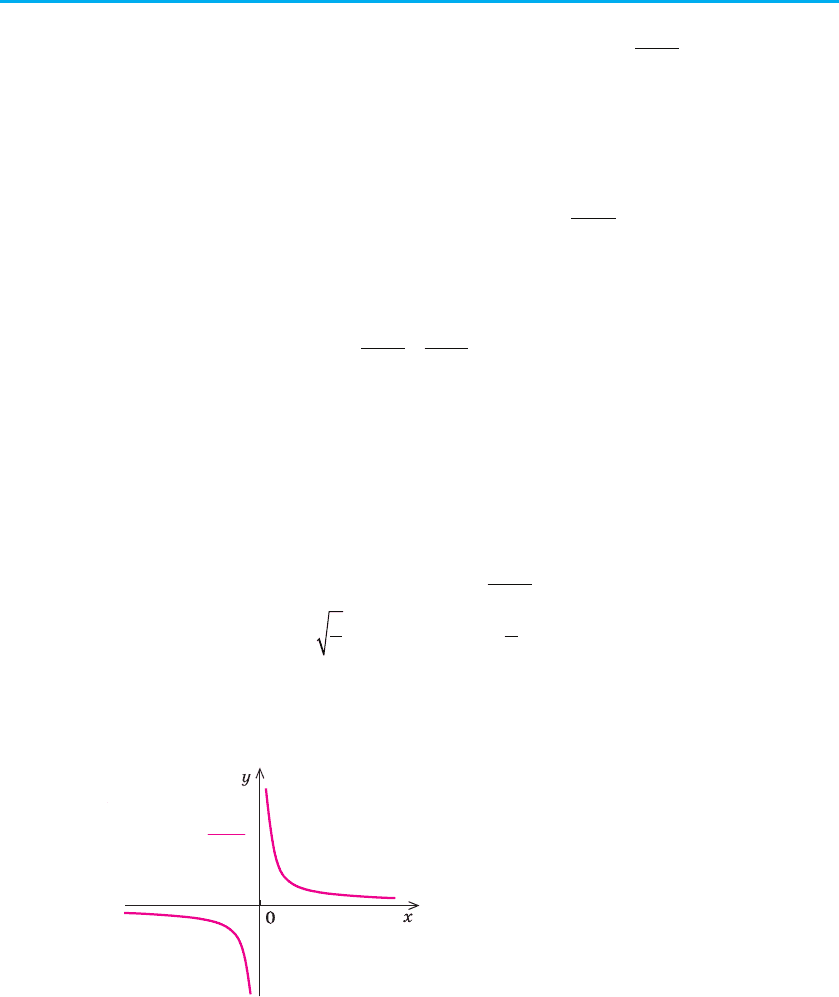
Ураховуючи властивості функції

y = x

–(2n – 1)

, п ∈ N, одержуємо її графік

(рис. 88).

4. Функція y = x

(α — парне від’ємне

число). Якщо α — парне від’ємне чис-

ло, то функція y = x

–2n

, п ∈ N, має

()

−−

−

∈

Рис. 88