Pati S.K., Enoki T., Rao C.N. R. (eds.) Graphene and Its Fascinating Attributes
Подождите немного. Документ загружается.

December 8, 2010 16:57 World Scientific Review Volume - 9in x 6in Chap8
Chapter 8
Phonons and Electron-Phonon Interaction
in Graphene and Nanotube
Tsuneya Ando
Department of Physics, Tokyo Institute of Technology,
2–12–1 Ookayama, Meguro-ku, Tokyo 152-8551, Japan
ando@phys.titech.ac.jp
A brief review is given on long-wavelength acoustic phonons, long-
wavelength optical phonons, and zone-boundary phonons in graphene
and carbon nanotubes together with effects of their interaction with
electrons from a theoretical point of view.
1. Introduction
Monolayer graphene was fabricated using the so-called scotch-tape tech-
nique
1
and the magnetotransport was measured including the integer quan-
tum Hall effect.
2,3
Since then the graphene became the subject of ex-
tensive theoretical and experimental study.
4,5
The carbon nanotube is
graphene rolled into a cylindrical form, discovered and synthesized ear-
lier than graphene.
6
The purpose of this paper is to give a brief review on
phonons and effects of electron-phonon interaction in graphene and nano-
tubes.
2. Monolayer Graphene and Nanotube
In a monolayer graphene the conduction and valence bands consisting of
π orbitals cross at K and K’ points of the Brillouin zone, where the Fermi
level is located.
7,8
Electronic states near a K point are described by the k·p
equation equivalent to Weyl’s equation or a Dirac equation with vanishing
rest mass.
6,9–14
In the vicinity of the K point, in particular, we have
γ(σ·
ˆ
k)F(r)=εF(r), F(r)=
F
A
(r)
F
B
(r)
, (1)
135
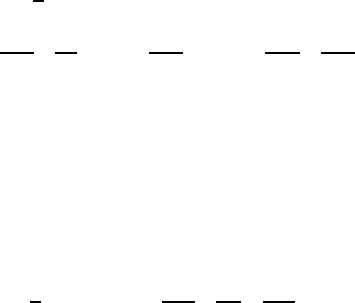
December 8, 2010 16:57 World Scientific Review Volume - 9in x 6in Chap8
136 T. Ando
where F
A
and F
B
describe the amplitude at sublattice points A and B,
respectively, γ is a band parameter,
ˆ
k=(
ˆ
k
x
,
ˆ
k
y
) is the wave-vector operator,
and σ =(σ
x
,σ
y
) is the Pauli matrix. The equation of motion for the K’
point is obtained by replacing σ with σ
∗
in the above equation.
Electronic states in a carbon nanotube (CN) are obtained by imposing
generalized periodic boundary condition F(r+L)=exp(∓2πνi/3)F(r) (up-
per sign for K and lower for K’) in the circumference direction specified by
chiral vector L with ν =0 or ±1 determined by the CN structure. We have
ν =0 for a metallic CN and ν = ±1 for a semiconducting CN. The direction
of L is called chiral angle and denoted by η.
3. Acoustic Phonon
Acoustic phonons important in the electron scattering are described well
by a continuum model.
15
The potential-energy functional for displacement
u=(u
x
,u
y
,u
z
) is written as
U[u]=
dxdy
1
2
B(u
xx
+u
yy
)
2
+ S
(u
xx
−u
yy
)
2
+4u
2
xy
, (2)
u
xx
=
∂u
x
∂x
+
u
z
R
,u
yy
=
∂u
y
∂y
, 2u
xy
=
∂u
x
∂y
+
∂u
y
∂x
, (3)
as in a homogeneous and isotropic two-dimensional (2D) system. The pa-
rameters B and S denote the bulk modulus and the shear modulus, respec-
tively (B = λ+µ and S =µ with λ and µ being Lame’s constants). In carbon
nanotubes with finite radius R, we should add u
z
/R in the expression of
u
xx
as in the above equation, where the x axis is chosen along the circum-
ference direction. In order to discuss out-of-plane distortions, we should
consider the potential energy due to nonzero curvature. It is written as
U
c
[u]=
1
2
a
2
Ξ
dxdy
∂
2
∂x
2
+
1
R
2
+
∂
2
∂y
2
u
z
2
, (4)
where Ξ is a force constant for curving of the plane. This curvature energy
is of the order of the fourth power of the wave vector and therefore is usually
much smaller than U[u].
In nanotubes, the phonon modes are specified by angular momentum
n along the circumference direction. Figure 1 shows phonon dispersions
calculated in this continuum model.
15
The twisting mode with a linear
dispersion and the stretching and breathing modes coupled with each other
at their crossing are given by the solid lines. There exist modes n = ±1
with frequency which vanishes in the long wavelength limit q →0. These
December 8, 2010 16:57 World Scientific Review Volume - 9in x 6in Chap8
Phonons and Electron-Phonon Interaction in Graphene and Nanotube 137
0.0 1.0 2.0 3.0 4.0
0.0
0.5
1.0
1.5
Wave Vector (units of R
-1
)
Frequency (units of ω
B
)
n
0
1
2
3
4
----- 5
Fig. 1. Frequencies of acoustic phonons obtained in the continuum model in carbon
nanotubes. ω
B
is the frequency of the breathing mode and R is the radius.
modes correspond to bending motion of the tube and therefore have the
dispersion ω ∝q
2
like a similar mode of a rod. Modes with other n involve
displacement from the circular shape of the tube cross section.
A long-wavelength acoustic phonon gives rise to an effective potential
called the deformation potential
V
1
= g
1
(u
xx
+u
yy
), (5)
proportional to a local dilation, where g
1
of the order of the Fermi level
measured from the bottom of the σ bands, i.e., g
1
∼ 30 eV. This term
appears as a diagonal term in the matrix Hamiltonian in the effective-mass
approximation and cannot give rise to backscattering in metallic nanotubes.
A higher order term appears due to the modification of local bond length,
V
2
= g
2
e
3iη
(u
xx
−u
yy
+2iu
xy
), (6)
where η is the chiral angle in nanotubes and vanishes in graphene, and
g
2
∼ γ
0
/2org
2
∼ 1.5 eV, which is much smaller than the deformation
potential constant g
1
. This term appears as an off-diagonal term. The
total Hamiltonian is written as
H
K
=
V
1
V
2
V
∗
2
V
1
, H
K
=
V
1
−V
∗
2
−V
2
V
1
. (7)
In the following, we shall discuss resistivity and/or conductivity limited
by these acoustic phonons in carbon nanotubes. In metallic nanotubes, V
1
does not give rise to backscattering as in the case of impurity scattering.
16,17
Further, phonon modes contributing to backscattering through V
2
depend
December 8, 2010 16:57 World Scientific Review Volume - 9in x 6in Chap8
138 T. Ando
10
-2
10
-1
10
0
10
1
10
2
10
-2
10
-1
10
0
10
1
10
2
Temperature (units of T
B
)
Resistivity (units of ρ
B
)
η
π/6 (Armchair)
π/12 (Chiral)
0 (Zigzag)
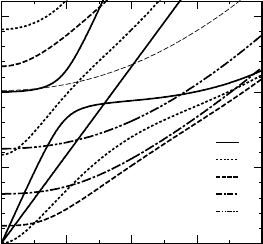
Fig. 2. The resistivity of armchair and
zigzag nanotubes in units of ρ
A
(T
B
)
which is the resistivity of the armchair
nanotube at T = T
B
,andT
B
denotes
the temperature of the breathing mode,
T
B
=ω
B
/k
B
.
0.0 1.0 2.0 3.0 4.0
0.0
0.5
1.0
Energy (units of 2πγ/L)
Conductivity (units of σ
A
(0))
g
1
/g
2
=10
Metal
Semiconductor
Fig. 3. Fermi-energy dependence of
conductivity for metallic and semicon-
ducting CN’s with g
1
/g
2
= 10 in units
of σ
A
(0) denoting the conductivity of an
armchair CN with ε =0.
on chirality η. In fact, transverse twisting modes contribute to the resis-
tivity, while longitudinal stretching and breathing modes contribute to it
in zigzag nanotubes. Figure 2 shows calculated temperature dependence
of the resistivity, where ρ
A
(T )=(/e
2
)R
−1
(g
2
2
k
B
T/2γ
2
S). The difference
between a zigzag and armchair nanotube appears at temperatures lower
than the frequency of the breathing mode ω
B
.
Figure 3 shows the Fermi-energy dependence of conductivity for metal-
lic and semiconducting CN’s. In metallic CN’s, when ε(2πγ/L)
−1
< 1, the
diagonal potential g
1
causes no backward scattering between two bands
with linear dispersion and smaller off-diagonal potential g
2
determines the
resistivity. However, when the Fermi energy becomes higher and the num-
ber of subbands increases, g
1
dominates the conductivity due to interband
scattering. This is the reason that the conductivity changes drastically de-
pending on the Fermi energy in metallic CN’s. On the other hand, such
a drastic change disappears for semiconducting CN’s and smaller conduc-
tivity compared to that of a metallic CN shows dominance of the diagonal
potential independent of the Fermi energy.
4. Optical Phonon
Long-wavelength optical phonons are known to be measured directly by
the Raman scattering.
18–20
Usually, they are described perfectly well in a
continuum model. Such a model was developed and the Hamiltonian for
electron-phonon interactions was derived,
21
and effects of electron-phonon
interaction on optical phonons were recently studied in graphene.
22,23

February 1, 2011 11:34 World Scientific Review Volume - 9in x 6in Chap8
Phonons and Electron-Phonon Interaction in Graphene and Nanotube 139
Optical phonons are represented by the relative displacement of two
sub-lattice atoms A and B,
u(r)=
q,µ
2NMω
0
(b
qµ
+ b
†
−qµ
)e
µ
(q)e
iq·r
, (8)
where N is the number of unit cells, M is the mass of a carbon atom, ω
0
is the phonon frequency at the Γ point, q =(q
x
,q
y
) is the wave vector,
µ denotes the modes (‘t’ for transverse and ‘l’ for longitudinal), and b
†
qµ
and b
qµ
are the creation and destruction operators, respectively. Define
q
x
= q cos ϕ
q
and q
y
= q sin ϕ
q
with q = |q|. Then, we have e
l
(q)=
i(cos ϕ
q
, sin ϕ
q
)ande
t
(q)=i(−sin ϕ
q
, cos ϕ
q
).
The interaction between optical phonons and an electron in the vicinity
of the K and K’ points is given by
21
H
K
int
= −
√
2
β
Γ
γ
b
2
σ×u(r), H
K
int
=+
√
2
β
Γ
γ
b
2
σ
∗
×u(r), (9)
where the vector product for vectors a =(a
x
,a
y
)andb =(b
x
,b
y
)in2Dis
defined by a×b = a
x
b
y
−a
y
b
x
. This means that the lattice distortion gives
rise to a shift in the origin of the wave vector or an effective vector potential,
i.e., u
x
in the y direction and u
y
in the x direction. The interaction strength
is characterized by the dimensionless coupling parameter
λ
Γ
=
36
√
3
π
2
2Ma
2
1
ω
0
β
Γ
2
2
. (10)
For M =1.993×10
−23
gandω
0
=0.196 eV, we have λ
Γ
≈3× 10
−3
(β
Γ
/2)
2
.
This shows that the interaction is not strong and therefore the lowest order
perturbation gives sufficiently accurate results.
The phonon Green’s function is written as
D
µ
(q,ω)=
2ω
0
(ω)
2
−(ω
0
)
2
−2ω
0
Π
µ
(q,ω)
. (11)
The phonon frequency is determined by the pole of D
µ
(q,ω). In the case
of weak interaction, the shift of the phonon frequency, ∆ω
µ
, and the broad-
ening, Γ
µ
,aregivenby
∆ω
µ
=
1
Re Π
µ
(q,ω
0
), Γ
µ
= −
1
Im Π
µ
(q,ω
0
). (12)
When we calculate the self-energy of optical phonons starting with the
known phonon modes in graphene, its direct evaluation causes a problem
of double counting.
24
In fact, if we apply the above formula to the case of
December 8, 2010 16:57 World Scientific Review Volume - 9in x 6in Chap8
140 T. Ando
0.0 0.5 1.0 1.5 2.0
-0.5
0.0
0.5
1.0
1.5
2.0
Fermi Energy (units of hω
0
)
Frequency Shift and Broadening (units of λω
0
)
Frequency Shift
Broadening
1/ω
0
τ
0.0
0.1
0.2
0.5
-1012
0.0
5.0
10.0
15.0
Frequency (units of λω
0
)
Spectral Function (units of 1/hω
0
)
0.0
1.0
2.0
3.0
4.0
Fermi Energy (units of hω
0
)
δ/hω
0
= 0.10
Frequency Shift
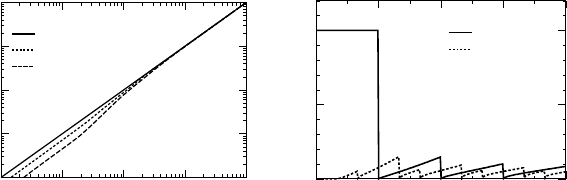
Fig. 4. (Left) The frequency shift and broadening of optical phonons in monolayer
graphene as a function of the Fermi energy. τ is a phenomenological relaxation time
characterizing the level broadening effect due to disorder. (Right) Calculated spectral
function of optical phonon for varying Fermi energy.
vanishing Fermi energy, we get the frequency shift due to virtual excita-
tions of all electrons in the π bands. However, this contribution is already
included in the definition of the frequency ω
0
. Inordertoavoidsucha
problem, we have to subtract the contribution in the undoped graphene for
ω =0 corresponding to the adiabatic approximation.
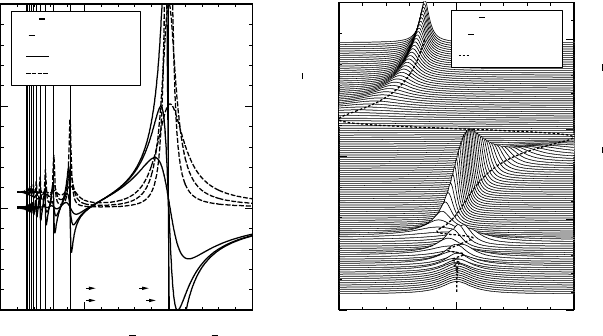
Figure 4 shows the frequency shift and broadening for various values
of 1/ω
0
τ and an example of the spectral function, (−1/π)ImD(q, ω
0
). For
nonzero δ or 1/ω
0
τ, the logarithmic singularity of the frequency shift and
the sharp drop in the broadening disappear, but the corresponding features
remain for 1/ω
0
τ 1. Similar results were reported independently
25
and
experiments giving qualitatively similar results were reported.
26–28
The calculation can easily be extended to the case in the presence of
magnetic field B, where discrete Landau levels are formed and oscilla-
tions due to resonant interactions appear in the frequency shift and the
broadening.
23
The Landau-level energy is given by ε
n
=sgn(n)
|n|ω
B
(n =0, ±1, ···), where sgn(n) denotes the sign of n and ω
B
=
√
2γ/l with
magnetic length l =
c/eB. Figure 5 shows calculated frequency shift
and broadening when ε
0
F
/ω
0
=1/4 and the corresponding phonon spec-
tral function, where ε
0
F
is the Fermi energy in the absence of a magnetic
field. All resonant transitions from −n to n+1 a n d f r o m −n−1ton with n>0
December 8, 2010 16:57 World Scientific Review Volume - 9in x 6in Chap8
Phonons and Electron-Phonon Interaction in Graphene and Nanotube 141
0.0 0.5 1.0 1.5
-5
0
5
10
Magnetic Energy: hω
B
(units of hω
0
)
Frequency Shift and Broadening (units of λω
0
)
-1 0
0
+1
-2
+1
-1
+2
ε
F
0
/hω
0
=0.250
δ/
hω
0
= 0.10 0.05 0.02
Frequency Shift
Broadening
-5 0 5
0
5
10
Frequency (units of λω
0
)
Spectral Function (units of 1/hω
0
)
0.0
0.5
1.0
1.5
Magnetic Energy: hω
B
(units of hω
0
)
ε
F
0
/hω
0
=0.250
δ/
hω
0
= 0.05
Frequency Shift
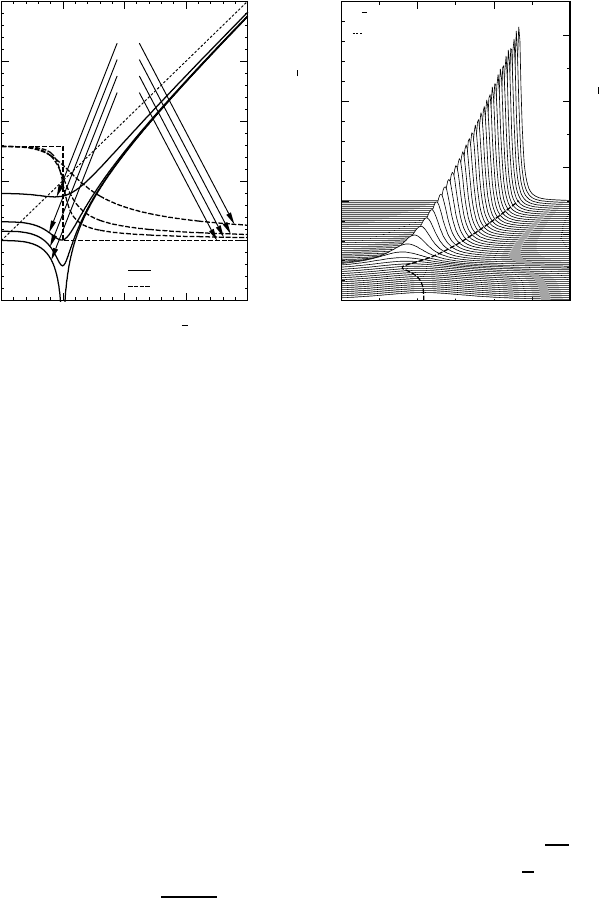
Fig. 5. (Left) The frequency shift and broadening of optical phonons in monolayer
graphene as a function of effective magnetic energy ω
B
. Thin vertical lines show res-
onance magnetic fields. ε
0
F
/ω
0
=1/4. The results for δ/ω
0
=0.1, 0.05, and 0.02 are
shown. (Right) The phonon spectral function for ε
0
F
/ω
0
=1/4andδ/ω
0
=0.05. The
dotted line shows the peak position as a function of ω
B
.
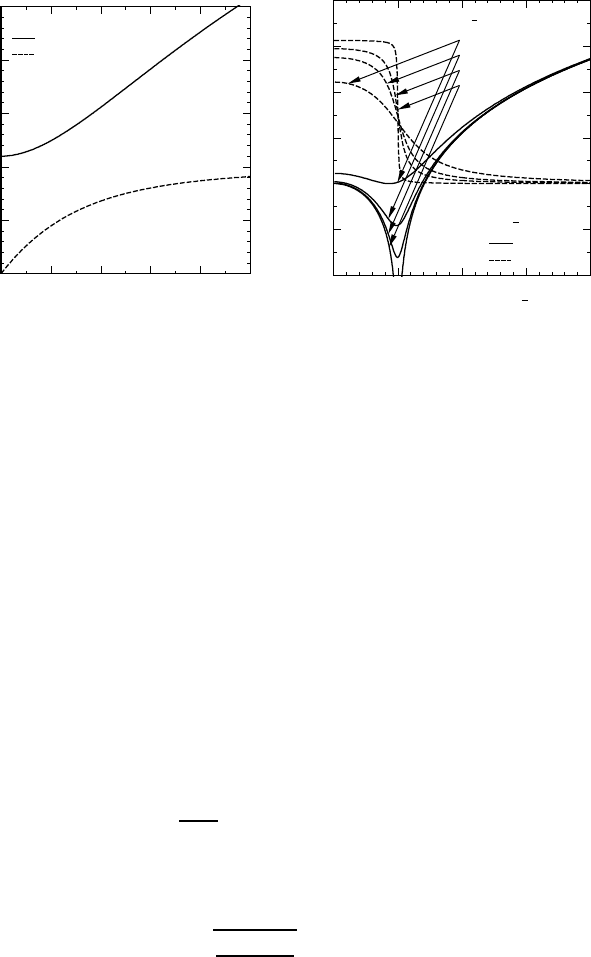
appear at the field where their energy difference becomes equal to ω
0
.At
resonances, the phonon spectrum exhibits characteristic behavior. Recently
this magneto-phonon resonance was observed in Raman experiments.
29
The same tuning of the optical-phonon frequency and broadening due
to change in the Fermi level is also possible in carbon nanotubes. In fact,
effects of the electron-phonon interaction on the optical phonon in carbon
nanotubes were theoretically studied earlier than in graphene.
21
In nan-
otubes, the modes are classified into longitudinal and transverse, depending
on their displacement in the axis or circumference direction. Figure 6 shows
the results of the similar calculations in carbon nanotubes.
30
In semiconducting nanotubes, the imaginary part vanishes identically
because of the presence of a gap. The frequency of the longitudinal and
transverse modes is both shifted to higher frequency side and the shift is
smaller for the longitudinal mode for small k
F
. The behavior of two modes
as a function of k
F
is similar to that of “level crossing.” In metallic nano-
tubes, the transverse mode is not affected by the doping at all. For the lon-
gitudinal mode, the energy shift exhibits a downward shift and considerable
broadening.
21
For nonzero k
F
, the self-energy has a logarithmic divergence
at γk
F
= ω
0
/2 and increases logarithmically with k
F
for γk
F
> ω
0
/2for
December 8, 2010 16:57 World Scientific Review Volume - 9in x 6in Chap8
142 T. Ando
0.0 0.1 0.2 0.3 0.4 0.5
0.0
0.5
1.0
1.5
2.0
2.5
Fermi Wave Vector (units of 2π/L)
Frequency Shift (units of α(L)ω
0
)
Semiconducting
Longitudinal
Transverse
0.0 0.5 1.0 1.5 2.0
-2
-1
0
1
2
3
4
Fermi Energy (units of hω
0
)
Frequency Shift and Broadening (units of α(L)ω
0
)
Longitudinal
E
φ
/hω
0
=0.00
Shift
Broadening
δ/
hω
0
0.500
0.200
0.100
0.010
Fig. 6. (Left) The frequency shift in a semiconducting nanotube as a function of the
Fermi wave vector k
F
. The solid and dashed lines represent the longitudinal and trans-
verse modes, respectively. (Right) The frequency shift and broadening of the longitudinal
mode in metallic nanotubes as a function of the Fermi energy.
vanishing δ. This behavior in CN, the same as in graphene theoretically
predicted
22,23,25,31
and experimentally observed,
26,27
was also observed in
Raman experiments
32,33
and discussed theoretically.
34,35
5. Zone-Boundary Phonon
Phonons near the K and K’ point, called zone-boundary phonons, can play
important roles in intervalley scattering between the K and K’ points. In
general, there exist four independent eigen modes for each wave vector.
However, after straightforward calculations, we can see that only one mode
with the highest frequency contributes to the electron-phonon interaction.
36
This mode is known as a Kekul´e type distortion generating only bond-length
changes. The interaction Hamiltonian is given by
H
int
=2
β
K
γ
b
2
0 ω
−1
∆(r)σ
y
ω∆
†
(r)σ
y
0
, (13)
where ω = e
2πi/3
and β
K
is another appropriate parameter, which is equal
to β
Γ
for the tight-binding model. In the second quantized form,
∆(r)=
q
2NMω
K
(b
Kq
+ b
†
K
−q
)e
iq·r
, (14)

December 8, 2010 16:57 World Scientific Review Volume - 9in x 6in Chap8
Phonons and Electron-Phonon Interaction in Graphene and Nanotube 143
where ω
K
is the frequency of the Kekul´e mode. It is worth noting that
∆ cannot be given by a simple summation over the K and K’ modes. We
should take a proper linear combination of the K and K’ modes in order to
make the lattice displacement a real variable. We can easily understand the
operator form of ∆ and ∆
†
in the interaction Hamiltonian by considering
the momentum conservation with the fact that 2K−K
and K−2K
are
reciprocal lattice vectors, where K and K
are the wave vectors at the K
and K’ point. The dimensionless coupling parameter, λ
K
,isgivenbythe
same expression as Eq. (10) except that ω
0
is replaced with ω
K
and β
Γ
with β
K
.Forω
K
= 161.2meV,wehaveλ
K
=3.5 × 10
−3
(β
K
/2)
2
.
The lifetime of an electron with energy ε is given by the scattering prob-
ability from the initial state to possible final states via emission and ab-
sorption of one phonon. For the zone-center phonon, the summation of the
contributions of longitudinal and transverse modes gives isotropic scattering
probability in each of the K and K’ points. For the zone-boundary phonon,
any scattering processes are classified into two types: One is the transition
between “one K-electron with one K-phonon” and “one K’-electron,” and
the other is between “one K-electron” and “one K’-electron with one K’-
phonon.” For example, an electron around the K point can be scattered to
the K’ point accompanied by absorption of one phonon around the K point,
and this belongs to the former process. The electron scattering from the K
to K’ point can also be induced by the emission of one phonon around the
K’ point, while this is classified into the latter one.
In graphene, the calculated scattering probabilities for both phonons
are given by the same formula,
τ
= πλ
α
|ε − ω
α
|. (15)
where α represents Γ or K and we have neglected the phonon occupation
due to large ω
α
at room temperature. This simply shows that the electron
lifetime is inversely proportional to the coupling parameter λ
α
and to the
density of states at the energy of the final state. What should be stressed
here is that the phonon emission is possible only when the energy of the ini-
tial electron is larger than that of the phonon to be emitted. Otherwise, the
final states are fully occupied at zero temperature and the phonon emission
never takes place. In this sense, the zone-boundary phonon has another ad-
vantage over the zone-center phonon. Therefore, the zone-boundary phonon
gives dominant scattering for high-field transport in graphene and in nan-
otube owing to its smaller frequency and larger coupling constant.
