Parinov I.A. Microstructure and Properties of High-Temperature Superconductors

Подождите немного. Документ загружается.

Macrostructure Modeling of Heat Conduction

C.1 Method of Summary Approximation

for Quasi-Linear Equation of Heat Conduction

For macrostructure modeling of the heat front propagation during sintering

and cooling of HTSC ceramic, the method of summary approximation (MSA)

is used as a method for construction of economic schemes for quasi-linear

non-stationary equations in the case of arbitrary region and any number of

measurements p [916].

The quasi-linear equation of heat conduction without heat sources (heat

capacity, c

, and material density, ρ, are suggested to be constant) has the

form:

∂u

∂t

= Lu; x =(x

,...x

) ∈ G, t > 0;

Lu =

α=1

u; L

u =

∂

∂x



(u, x

)

∂u

∂x



; k

≥ C

> 0(C.1)

with boundary and initial conditions:

= μ(x, t); u(x, 0) = u

(x); x ∈ G, (C.2)

where u is the temperature; x

are the spatial coordinates; t is the time and

α is the ﬁxed coordinate direction. A boundary Γ of a region G is suﬃciently

smooth, which is necessary for the existence of smooth solution, u = u(x, t).

It is assumed that smooth derivations are required.

As it is made in all economic schemes, the process of approximate solution

for multidimensional problem is divided into several stages. Simple problem

is solved at every stage. The operator L is presented by the operator sum of

more simple structures:

L =

α=1

. (C.3)

516 C Macrostructure Modeling of Heat Conduction

We consider multidimensional equation (C.1) and compare to problem

(C.1), (C.2) a “chain” of equations:

α=1

u =0; P

u =

∂u

∂t

− L

u. (C.4)

At the interval, 0 ≤ t ≤ t

, an uniform lattice, 

= {t

= jτ; j =

0, 1,...,j

} with a step, τ = t

, is introduced. Every interval is divided into

p parts, introducing points t

j+α/p

= t

+ατ/p; α =1, 2,...,p−1. Successively

(at α =1, 2,...,p),

(α)

=0; x ∈ G; t ∈ (t

j+(α−1)/p

; t

j+α/p

]; α =1, 2 ...,p , (C.5)

are solved suggesting

(1)

(x, 0) = u

(x); V

(α)

(x, t

j+(α−1)/p

)=V

(α−1)

(x, t

j+(α−1)/p

) . (C.6)

Also, it is assumed that the boundary condition of ﬁrst type is given at Γ.

The solution of this problem is named

V (x, t

)=V

(p)

(x, t

); j =0, 1,...,j

. (C.7)

Every of the equations, P

(α)

= 0, it is substituted by the diﬀerence

scheme (approximating

∂u

∂t

and L

by corresponding diﬀerence relations at

uniform lattice ω

with steps h

,...,h

)

(α)

=0; α =1, 2,...,p. (C.8)

The scheme (C.8) approximates the equation P

(α)

= 0 in usual sense,

that is

j+α/p

− (P

j+α/p

→ 0, at τ → 0andh

→ 0 . (C.9)

The summary approximation of additive scheme (C.8) is attained due

to the “chain” of diﬀerential equations (C.5), and (C.6) approximates corre-

sponding equations (C.5) in usual sense.

Then, it is assumed that L

consists of derivations only on variable x

Therefore, L

is the one-dimensional operator, P

(α)

= 0 are the one-

dimensional equations and additive scheme (C.8) is the local one-dimensional

scheme (LOS). We write LOS, and with this aim the multidimensional equa-

tion is replaced by “chain” of one-dimensional equations:

∂V

(α)

∂t

= L

(α)

, (C.10)

j+(α−1)/p

<t≤ t

j+α/p

; α =1, 2 ...p; x ∈ G; t

j+α/p

=(j + α/p)τ,

(C.11)

C.1 Method of Summary Approximation for Quasi-Linear Equation 517

with conditions

(1)

(x, 0) = u

(x); V

(α)

(x, t

j+(α−1)/p

)=V

(α−1)

(x, t

j+(α−1)/p

);

(α)

= μ(x, t), at x ∈ Γ

. (C.12)

For diﬀerence approximation of the operator L

in node x

, a three-point

templet is used, consisting of the points: x

(−1α)

(+1α)

where x

(±1α)

)

,...,x

)

±h

,...,x

)

]; x

)

= h

; h

is the step of the lattice ω

α-direction. A number of internal nodes of the lattice ω

consists of the points

x =(x

,...,x

) ∈ G of crossing of the hyper-planes x

= i

; i

0, ±1, ±2,...; α =1, 2,...,p, but a number of boundary nodes γ

consists of

the points of crossing of the straight lines C

, passing through all internal

nodes x ∈ ω

, with boundary Γ . Also introduced are the next designations:

h,α

is the number of boundary nodes in direction x

; γ

is the number of all

boundary nodes x ∈ Γ .

Let

G = { 0 ≤ x

≤ l

} is the parallelepiped, then Γ

consists of the

facets: x

=0andx

= l

. Approximating every heat conduction equation

of number α at semi-interval (t

j+(α−1)/p

; t

j+α/p

] by a two-layer scheme with

weights, a “chain” of p one-dimensional schemes is stated that is called LOS:

j+α/p

− y

j+(α−1)/p

= Λ

[σ

j+α/p

+(1− σ

j+(α−1)/p

] , (C.13)

where α =1, 2,...,p; x ∈ ω

; σ

∈ [0, 1].

In regular nodes, Λ

has second order of approximation, Λ

u − L

u =

O(h

), and in non-regular nodes, Λ

u−L

u = O(1). Consider purely implicit

LOS (σ

≡ 1):

j+α/p

− y

j+(α−1)/p

= Λ

j+α/p

, (C.14)

and join to this equation the boundary condition:

j+α/p

= μ

j+α/p

, at x ∈ γ

h,α

; j =0, 1,...,j

; α =1, 2,...,p, (C.15)

and initial condition:

y(x, 0) = u

(x) . (C.16)

Let us assume y

is known. In order to deﬁne y

j+1

at new layer from (C.14)

and (C.15), the p equations (C.14) are required to solve together with the

boundary condition (C.15), successively suggesting α =1, 2,...,p.Inorder

to deﬁne y

j+α/p

, we have the boundary-value problem:

j+α/p

−1

− C

j+α/p

+ A

j+α/p

=0, at x ∈ ω

; (C.17)

j+α/p

= μ

j+α/p

, at x ∈ γ

h,α

; α =1, 2,...,p. (C.18)

Here, the lower indexes are pointed only, which change in calculations. The

diﬀerence equation is written along the section of the straight line, the ends

518 C Macrostructure Modeling of Heat Conduction

of which coincide with the nodes γ

h,α

. Equation (C.17) is solved by the run

method at ﬁxed α-direction along corresponding sections. Successively sug-

gesting α =1, 2,...,pand changing the run directions, y

j+1/p

j+2/p

,...,y

j+1

are calculated, expending O(1) operations per lattice node. Thus, the LOS

(C.14)–(C.16) is economic [916]. Moreover, it can be shown that the LOS ap-

proximation error tends to zero at τ → 0andh

→ 0, and from summary

approximation, uniform convergence of the LOS with rate, O



τ +max

1≤α≤p



is followed [916].

C.2 Heat Conduction of Heterogeneous Systems

A study of heat conduction of the heterogeneous systems is a suﬃciently

complex problem. In the case of HTSC ceramics, it is even more complicated

due to signiﬁcant porosity and diﬀerent, compared to metal, mechanism of

heat conduction. In metal, demonstrating a small porosity and high heat con-

duction of crystallites, the main mechanism of heat conduction is the convec-

tion. In oxide superconductors, possessing relatively greater porosity, together

with heat transfer on solid component, the main sources of heat transfer are

molecular and radiant components of heat conduction.

C.2.1 Eﬀective Heat Conduction of Mixes

and Composites

Existing mixes and composites can be presented by one of the models, depicted

in Fig. C.1. A process of ceramic sintering can be described by using structure

with mutual-penetrating components (see Fig. C.1b) and the loose granu-

lar material (see Fig. C.1e). All components of the structure with mutual-

penetrating components are continuous in any direction and geometrically

equivalent relative to eﬀective heat conduction:

= f

(λ

,λ

)=f

(λ

,λ

), at m

= m

, (C.1)

where λ

and m

(i =1, 2) are the heat conduction and concentration of the

components.

Granular materials consist of monolithic particles (1) (see Fig. C.1e) and

occupy an intermediate state between the structures with impregnation and

the structures with mutual-penetrating components. The contacting particles

and pores (2), disposed between them, form continuous extent of solid com-

ponents and cavities in any direction.

Following [234], deﬁne heat conduction of granular system. First, consider

a structure with mutual-penetrating components. In order to take into account

the distortion of the heat ﬂux lines, we use the following formulae for eﬀective

C.2 Heat Conduction of Heterogeneous Systems 519

(a)

(c)

(d)

(e)

(b)

Fig. C.1. Heterogeneous systems with diﬀerent structure: (a) impregnated struc-

ture; (b) structure with mutual-penetrating components; (c, d) combined structures

with mutual-penetrating components and impregnation; (e) loose granular material

heat conduction in the cases of adiabatic and isothermal division of elementary

cell, respectively:

= λ



+ ν(1 − c)

2c(1 − c)ν

1+c(ν − 1)



,ν= λ

/λ

;(C.2)

= λ



1 − c

+ ν(1 − c

)

c(2 − c)+ν(1 − c)



−1

. (C.3)

here c is the solution of the equation:

=2c

− 3c

+1;m

=1− m

. (C.4)

520 C Macrostructure Modeling of Heat Conduction

Hence

c =0.5+A cos(ϕ/3) , (C.5)

where

A =



−1; ϕ = arccos (1 − 2m

), at 0 ≤ m

≤ 0.5;

1; ϕ = arccos (2m

− 1), at 0.5 ≤ m

≤ 1 ,

(C.6)

and 3π/2 ≤ ϕ ≤ 2π. Then, eﬀective heat conduction is deﬁned as

=(λ

+ λ

)/2 . (C.7)

The approximate solution (C.7) gives values, which are near to numerical

results and preserves property of component invariability.

C.2.2 Polystructural Model of Granular Material

A heat transfer into pores occurs due to molecular collisions and radiation.

At the same time, convection is absent, as a rule. The molecular transfer of

heat takes place due to interchange by kinetic energy at collisions of moving

molecules with one another and with surface of solid or liquid component,

limiting pores (grain and liquid surfaces). The heat transfer due to radiation

occurs on account of the absorption, emission and dissipation of radiant en-

ergy. Both mechanisms can exist together and inﬂuence each other mutually.

The granular structure of ceramic powder consists of “frame” (1) (see

Fig. C.1e), formed by the chaotic, but relatively dense package of continuously

contacting grains (the structure of ﬁrst order) and spatial lattice of more larger

cavities (2), penetrating the powder, which together with the frame form the

structure of second order with mutual-penetrating continuous components.

Not destroying generality, it may be assumed that the structure of second

order occurs at m

≥ 0, 4 [235].

First, a dependence of coordination number, N

(i.e., number of contacts

per one particle) on the porosity m

is deﬁned. For this, a granular system is

considered, consisting of convex rounded particles. In all points of the particle

contacts, we depict tangential planes. Then, volume of the system is divided

into polyhedrons, circumscribed around any particle. In this case, the facet

number of every polyhedron is equal to the number of contacts for given

particle (Fig. C.2a).

The porosity of the system is presented through ratio of the diﬀerence be-

tween volumes of all polyhedrons and particles to volume of the polyhedrons.

Determination of required dependence for the parameter N

is carried out, us-

ing arbitrary polyhedron, circumscribed around particle with mean radius, r.

Then, N

is the mean coordination number for all polyhedrons of the system.

For chaotic actual structure, it is assumed that all contacts are uniformly

distributed on particle surface. Then, it is suggested that the polyhedron con-

sists of N

identical pyramids with tops at the particle center (Fig. C.2b). In

this case, mean porosity of pyramid is equal to mean porosity of the granular

system. For simplicity, the pyramid is substituted by cone with the same solid

C.2 Heat Conduction of Heterogeneous Systems 521

(a)

(b)

(c)

Fig. C.2. Substitution procedure used for deﬁnition of coordination number as

function of porosity: (a) polyhedron formed due to crossing the planes tangential

to particle in contact points; (b) pyramid is the element of polyhedron; (c) straight

circular cone

angle and around-contact surfaces are replaced by spherical ones (Fig. C.2c).

Then, the porosity of this system is equal to

=1− V

; V

=0.33πr

r, (C.8)

where V

is the cone volume; V

is the ball sector in the cone; r

is the

radius of the cone base: and r is the radius of the spherical surface.

In order to deﬁne r

, we use equalities: F

= F

=2πrh

. Hence

=2r/N

, (C.9)

where F

are the surface squares of the ball and ball segment and h

the segment height. Because ΔOAB is similar to ΔOCD, then from (C.9), we

obtain

=2r(N

− 1)

1/2

/(N

− 2) . (C.10)

The volume of the ball sector is smaller by N

times than the volume of

the ball

=4πr

/3N

. (C.11)

By using the formula for N

and (C.8), (C.10) and (C.11), we obtain ﬁnally

=[m

+3+(m

− 10m

+9)

1/2

]/2m

. (C.12)

Then, eﬀective heat conduction of the structure of second order with

mutual-penetrating components is calculated by using (C.2), reduced to the

form

λ = λ



+ ν

(1 − c

)

2ν

(1 − c

)

+1− c



; ν

= λ

/λ

. (C.13)

Here, the geometrical parameter c

characterizes volume concentration of

frame and is connected with the porosity, m

(in the second order structure),

throughanequationoftype(C.4):

=2c

− 3c

+1. (C.14)

522 C Macrostructure Modeling of Heat Conduction

The volume concentration of pores, m

, in granular system with volume

V and pore volume V

is equal to m

= V

/V , but the porosities of the frame,

, and the second order structure, m

, are found as

= V

/(V

+ V

); m

= V

/V , (C.15)

where V

and V

are the volumes of particles, pores in the frame and

pores in the second order structure.

Moreover, there are next relations:

V = V

+ V

; V

= V

+ V

. (C.16)

Then, we obtain from (C.15) and (C.16)

=(m

− m

)/(1 − m

) . (C.17)

In order to calculate heat conduction, using (C.13), it is necessary to know

the heat conduction of component, ﬁlling pores of the second order structure,

, and heat conduction of the frame, λ

.Thevalueofλ

is the sum of

molecular and radiant components. It depends both on the physical proper-

ties of gas and on the geometrical and physical parameters of the pores. For

structure of granular material, the molecular component is calculated as [234]

1+B/(Hδ

)

, (C.18)

where δ

=3d(1 − c

)/c

is the mean size of great cavities; d =2r is the

grain diameter;

B =

4γ(2 − a)Λ

(γ +1)aPr

;

where λ

is the heat conduction factor of gas in the inﬁnite space at pressure

H and temperature T ; a is the accommodation factor of gas at uniform walls;

is the mean length of the gas molecule run; γ = c

is the adiabatic

index, being a ratio of isobaric heat capacity to isochoric; Pr = ν/k is Prandtl’s

criterion, being the ratio of kinematic viscosity, ν, to temperature conductivity

of gas, k.

Relation for radiant component of the heat conduction factor in pores of

the second order structure has the form [234]:

≈ 0.23(T/100)

(1 − c

)(2 − ε)

, (C.19)

where Y = f(τ, ε) is the function, taking into account inﬂuence of the optic

thickness of sample, τ = βl

, and of the blackness degree, ε, limiting surfaces

(walls); for “gray” approximation, β = α

+ γ

is the spectrum factor of

weakening; α

and γ

are the volume spectrum factors of absorption and

scattering; l

is the thickness of ﬁlling layer. The value Y ≈ 1 for granular

C.2 Heat Conduction of Heterogeneous Systems 523

systems with porosity m

< 0.95 [234]. We obtain from (C.18) and (C.19)

relation for the heat conduction of gas component in pores of the second

order structure:

= λ



3Hd(1 − c

)



−1

+0.23(T/100)

(1 − c

)(2 − ε)

. (C.20)

C.2.3 Model of Granular System with Chaotic Structure

In order to model the granular system with chaotic structure, consider a sys-

tem consisting of rounded absolute solid particles with heat conduction fac-

tors, that are greater than corresponding parameter of component, occupying

pores. Main fraction of heat ﬂux passes through the regions, surrounding point

contacts of particles (the sizes of near-contact regions are much smaller than

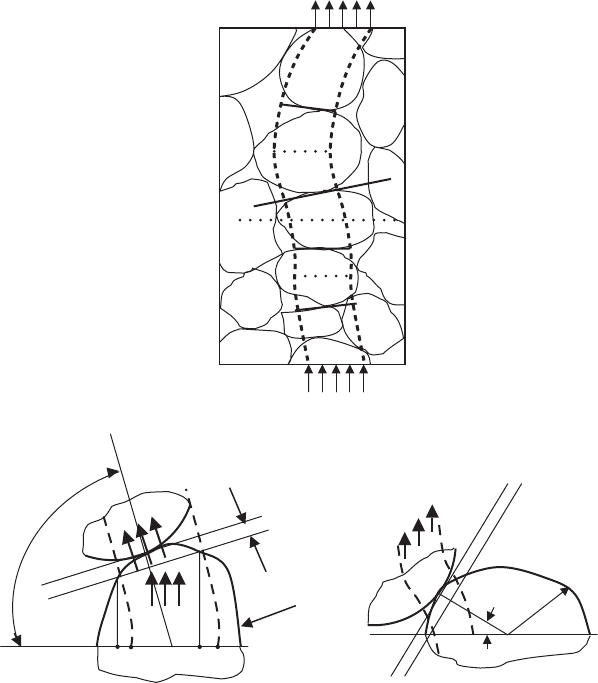
grain diameter). Then, we divide the heat ﬂux into single ﬂux tubes, so that

the tube axis in every particle passes successively the near-contact regions at

entry and exit of the ﬂux (Fig. C.3a).

Assumption 1. Heat conduction of any tube is equal to eﬀective heat con-

duction of all granular system.

It is assumed that the tube length is much more greater than the cross-

section length of particles with non-elongated shape, which ﬁll the granular

system volume chaotically. We divide the tube into elements: i −1,i,i+1,....

Every element is limited by two planes perpendicular to the heat ﬂow,

namely the plane in contact point and the plane δ–δ, dividing particle in

half (Fig. C.3). The lateral surface of the tube is formed by adiabatic surface.

Thermal resistance of the tube is equal to the sum of thermal resistance

of its elements, which are divided into two types. The elements without

(ﬁrst type) and with (second type) through pores are shown respectively in

Fig. C.3b and c. The through pores are present in only those elements of the

tube (second type) for which a–a plane (Fig. C.3c) contacts with δ–δ plane

within tube.

The averaged element for case of the ordered cubic package of balls is

shown in Fig. C.4a. Any ball contacts with six other balls in the points K, L,

M, N, O, P. Four contacts (points M, N, O, P) belong to through pores; the

cross-section area of the through pores is shaded.

First, consider a heat transfer in the elements of ﬁrst type (with distorted

boundaries of elements). Let the thermal resistance of the distorted element

) (see Fig. C.3b) be the resistance of “straightened” element

ABB

) with the lateral adiabatic surfaces parallel to the direction

of general heat ﬂux, but cross-section square is the same as initial element

square. Then, the distortion of ﬂux lines in the “straightened” element occurs

only in the plane of near-contact region.

Assumption 2. The near-contact regions of particle in any element of ﬂux

tube are formed by spherical surfaces with mean radius r.

524 C Macrostructure Modeling of Heat Conduction

+ 1

i + 2

(a)

i – 1

– 3

– 2

(c)

•

(b)

δδ

Fig. C.3. Account of chaotic character of particle package in frame: (a) ﬂux tubes

in the frame; (b) element of the ﬂux tube of 1st type; (c) element of the ﬂux tube

of 2nd type

The square of spherical surface per contact, S

, is the equal to ratio of

total square of the particle surface, S =4πr

, to the coordination number,

,thatis,S

=4πr

. A cross-section of grain part in the ﬂux tube is

presented in the form of circle with radius r

(Fig. C.4c). Dependency between

parameters r

and N

is stated, taking into account the following relations:

= h

(2r − h

); S

=2πrh

, (C.21)

where h

is the height of ball segment. Hence

= r

/r =2(N

− 1)

1/2

. (C.22)