Pao Y.C. Engineering Analysis: Interactive Methods and Programs with FORTRAN, QuickBASIC, MATLAB, and Mathematica

Подождите немного. Документ загружается.

FIGURE 9. Problem 20.

FIGURE 10. Problem 21.

FIGURE 11. Problem 22.

1.7 REFERENCE

1. Y. C. Pao, “On Development of Engineering Animation Software,” in Computers in

Engineering, edited by K. Ishii, ASME Publications, New York, 1994, pp. 851–855.

FIGURE 12. Problem 23.

Exact, Least-Squares, and

Cubic Spline Curve-Fits

2.1 INTRODUCTION

Engineers conduct experiments and collect data in the laboratories. To make use of

the collected data, these data often need to be ﬁtted with some particularly selected

curves. For example, one may want to ﬁnd a parabolic equation y = c

+ c

x + c

which passes three given points (x

) for i = 1,2,3. This is a problem of

exact curve-

ﬁt

. Or, since knowing in advance that these three points should all fall on a straight

line, but the reason that they are not is because of bad calibration of the measuring

equipment or because of presence of noises in the testing environment.

In case that we may want express this straight line by the equation y = c

+ c

for the stress and strain data collected for a stretching test of a metal bar in the

elastic range, then the question of how to determine the two coefﬁcients c

and c

is a matter of deciding on which criterion to adopt. The

Least-Squares

method is

one of the criteria which is most popularly used. The two cases cited are the

consideration of adopting the two and three lowest

polynomial

terms, x

, x

, and x

and linearly combining them.

If the collected data are supposed to represent a sinusoidal function of time, the

curve to be determined may have to be assumed as x(t) = c

sint + c

sin3t + c

sin5t

+ c

sin7t by linearly combining 4 odd sine terms. This is the case of selecting four

particular functions, namely, f

(t) = sin(2i–1)t for i = 1,2,3,4., and to determine the

coefﬁcients c

1–4

by application of the least-squares method.

Often some special form of curve needs to be selected to ﬁt a given set of data,

the least-squares criterion can still be applied if mathematical transformations can

be found to convert the equation describing the curve into linear equations. This is

discussed in a section devoted to transformed least-squares curve-ﬁt.

Another commonly applied curve-ﬁt technique is the cubic spline method which

allows smooth cubic equations to be derived to ensure continuous slopes and cur-

vatures passing all given points. The mathematics involved in this method will be

presented.

In the following sections, we shall discuss the development of the programs

ExactFit

LeastSq1

LeastSqG

, and

CubeSpln

for the four curve-ﬁt needs men-

tioned above.

2.2 EXACT CURVE FIT

As another example of solving a matrix equation, let us consider the problem

of ﬁnding a parabolic equation y = c

+ c

x + c

which passes three given points

) for i = 1,2,3. This is a problem of

exact curve-ﬁt

. By simple substitutions of

the three points into the parabolic equation, we can obtain:

(1)

In matrix form, we write these equations as:

(2)

where {C} = [c

]

, {Y} = [y

]

, and [A] is a three-by-three coefﬁcient

matrix whose elements if denoted as a

i,j

are to be calculated using the formula:

(3)

It is easy to extend the above argument for the general case of exactly ﬁtting N

given points by a N-1st degree polynomial y = c

+ c

x + ••• + c

N–1

. The only

modiﬁcation needed is to allow the indices i and j in Equations 1 and 3 to be extended

to reach a value of N. A program called

ExactFit

has been prepared for this need

by utilizing the subroutine

GauJor

to solve for the vector {C} from Equation 1 for

the general case of exactly ﬁtting N given points. Listings for both

FORTRAN

and

QuickBASIC

versions along with sample numerical results are presented below.

FORTRAN V

ERSION

ccxcx y i

iii

12 3

123++= =for , ,

AC Y

[]

{}

ax ij

ij i

,,,==

−1

123for

Sample Applications

UICK

BASIC V

ERSION

Sample Application

MATLAB Application

For handling the exact curve ﬁt of N given points with a N-1st degree polynomial,

there is no need to convert either the

FORTRAN

QuickBASIC

program

Exact-

Fit

. The sample problems therein can be readily solved by

MATLAB

as follows:

Notice that the coefﬁcient {C} for the curve-ﬁt polynomial is obtained by

solving [A]{C} = {Y} where matrix [A] is formed by substituting the X values

into the x

terms for i = 0 to N–1 where N is the number of points provided.

MATLAB

function

ones

has been used to generate the ﬁrst column of [A] and

MATLAB

matrix operation of C = A\Y which premultiplies {Y} by [A]

–1

obtain {C}.

Also, this exact curve-ﬁt problem can be treated as a special case of ﬁtting N

given points by a linear combination of N selected functions which in this case

happens to be the polynomial terms of x

to x

N–1

, by the least-squares method. A m

ﬁle called

LeastSqG.m

which is discussed in the program

LeastSqG

can be readily

applied to treat such a exact curve-ﬁt problem. Here, we demonstrate how

Least-

SqG.m

is used by

MATLAB

interactive operation in solving the sample problems

previously presented in the

FORTRAN

and

QuickBASIC

versions of the program

ExactFit

. First, a function must be prepared to describe the ith selected function x

as follows:

The results of four

MATLAB

applications are:

Notice the coefﬁcient vector {C} in the curve-ﬁt polynomial p(x) = c

+ c

x +

… + c

N–1

is solved from the matrix equation [A]{C} = {R} where {A} and {R}

are generated using the speciﬁed points based on the least squares criterion. The

solution of [A]{C} = {R} is simply implemented by

MATLAB

with the statement

C = A\R in the ﬁle LeastSqG.m.

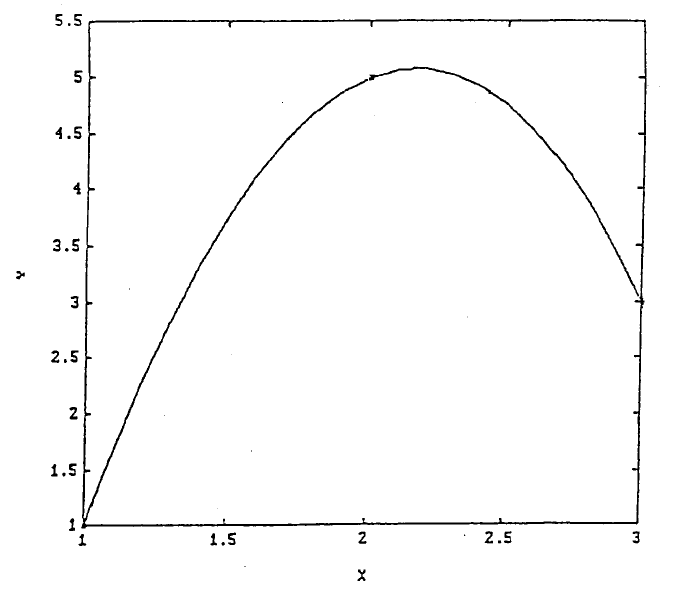
To verify whether the points have really been ﬁtted exactly, Figure 1 is presented.

It is plotted with the following

MATLAB

statements, adding to those already listed

above:

Notice that for application of polyval.m,

MATLAB

needs the coefﬁcients of the

polynomial arranged in descending order. Since the array C contains the coefﬁcients

in ascending order, a new array called Creverse is thus created for calculation of the

curve values for 1

≤

3 and with an increment of 0.1. Figure 1 shows that the

parabolic curve passes through all of the three given points.

2.3 PROGRAM LEASTSQ1 — LEAST-SQUARES LINEAR CURVE-FIT

Program

LeastSq1

is designed for curve-ﬁtting of a set of given data by a linear

equation based on the least-squares criterion.

If only two points are speciﬁed, a

linear equation which geometrically describes a straight line can be uniquely derived

because the line must pass the two speciﬁed points. This is the case of

exact ﬁt

. (See

programs

Gauss

and

LagrangI

for examples of exact ﬁt.) However, the speciﬁed

data are often recorded from a certain experiment and due to inaccurate calibration

of equipment or due to environmental disturbances such as noise, heat, and so on,

these data not necessarily follow an expected behavior which may be described by

a type of predetermined equation. Under such a circumstance, a so-called

forced ﬁt

is then required. As a simple example, supposing that we expect the measured set

of three data points (X

) for i = 1,2,3 to satisfy a linear law Y = c

+ c

X. If these

three points happen to fall on a straight line, then we have a case of exact ﬁt and

FIGURE 1.

The parabolic curve passes through all of the three given points.