Ответы на экзаменационные вопросы по курсу: Эконометрика

Подождите немного. Документ загружается.

Явление гетероскедастичности возникает, как правило, при анализе неоднородных объектов. Например, при

построении зависимости прибыли фирмы от размера основного фонда (или каких-либо других факторов)

гетероскедастичность вызвана тем, что у больших фирм колебания прибыли будут выше, чем у малых.

МНК при наличии гетероскедастичности позволяет получить несмещенные оценки параметров модели, но оценка

дисперсии ошибки, и, следовательно, границы доверительных интервалов оценок параметров модели и прогноза

зависимой переменной будут неверными, т.к. они вычисляются на основании предположения гомоскедастичности

ошибок.

Для проверки на гетероскедастичность существует большое число тестов. Мы остановимся на тсте Голдфельда-

Квандта.

Тест Голдфелъда-Квандта применяется в том случае, когда имеются предположения:

1. о прямой зависимости дисперсии σ

, ошибки регрессии ε

от величины некоторой независимой переменной X в

наблюдении t;

2. случайный член ε

, распределен нормально и не подвержен автокорреляции.

Алгоритм теста:

1. Упорядочивание n данных в выборке по величине независимой переменной, относительно которой есть

подозрение на гетероскедастичность.

2. Исключение с средних наблюдений в этом упорядочении в целях построения двух независимых "частных"

регрессий по данным n' = (n-с)/2 в начале выборки и по данным n' = (n - с)/2 в конце выборки

3. Проведение двух независимых "частных" регрессий - первых n' и последних n' наблюдений и построение

соответствующих остатков е

и е

;

4. Вычисление сумм квадратов остатков "частных" регрессий: е

'е

, е

'е

. Если предположение относительно природы

гегероскедастичности верно, то дисперсии ошибок регрессии в последних n' наблюдениях будут больше (меньше),

чем в первых n' наблюдениях при прямой (обратной) пропорциональной зависимости между σ

и X

и это скажется

на сумме квадратов остатков в рассматриваемых частных регрессиях. Поэтому в качестве теста на выявление

гетероскедастичности остатков регрессии предлагается использовать статистику F, вид которой определяется

предположением зависимости между дисперсией ошибок регрессии σ

и регрессором X

F = е

'е

/ е

'е

- в случае обратной пропорциональности

F = е

'е

/ е

'е

- в случае прямой пропорциональности.

Статистика F имеет распределение Фишера с (n'- k- 1) степенями свободы, где k- число объясняющих переменных

в регрессионном уравнении. Если значение статистики превышает критически значение при определенном уровне

значимости, то нулевая гипотеза Н

об отсутствии гетероскедастичности отвергается.

Тест ранговой корреляции Голдфелда-Квандта позволяют обнаружить лишь само наличие гетероскедастичности,

но они не дают возможности проследить количественный характер зависимости дисперсий ошибок регрессии от

значений регрессоров и, следовательно, не представляют каких-либо способов устранения гетероскедастичности.

При использовании этого теста предполагается, что дисперсии ошибок регрессии представляют собой одну и ту же

функцию от наблюдаемых значений регрессоров, т.е.



= f

.,1 ni 

(1)

Чаще всего функция f выбирается квадратичной, что соответствует тому, что средняя квадратичная ошибка

регрессии зависит от наблюдаемых значений регрессоров приближенно линейно. Гомоскедастичной выборке

соответствует случай f = const.

Идея теста Уайта заключается в оценке функции (1) с помощью соответствующего уравнения регрессии для

квадратов остатков:

,)(

iii

uxfe 

ni ,1

, где u

– случайный член. (2)

Гипотеза H

об отсутствии гетероскедастичности (условие f = const) принимается в случае не значимости

регрессии (2) в целом.

a) Итак, сначала к исходной модели применяется обычный МНК;

b) Находятся остатки e

ni ,1

регрессии;

c) Осуществляется регрессия квадратов этих остатков e

на все регрессоры x вида (2);

d) Осуществляется регрессия квадратов этих остатков e

на квадраты регрессоров x

;

e) Осуществляется регрессия квадратов этих остатков e

на попарные произведения регрессоров;

Для пунктов c) – e) считается F – статистика, если

;1;; 



pnp



где p – количество регрессоров, то гипотеза

об отсутствии гетероскедастичности отклоняется.

Заметим, что на практике применение теста Уайта с включением и не включением попарных произведений дают,

как правило, один и тот же результат.

Привлекательной чертой теста является его универсальность. Однако, если гипотеза H

об отсутствии

гетероскедастичности отклоняется, этот тест не дает указания на функциональную форму гетероскедастичности.

35. Системы регрессионных (одновременных) уравнений.

При статистическом моделировании экономических ситуаций часто необходимо построение систем уравнений,

когда одни и те же переменные в различных регрессионных уравнениях могут одновременно выступать, с одной

стороны, в роли результирующих, объясняемых переменных, а с другой стороны - в роли объясняющих

переменных. Такие системы уравнений принято называть системами одновременных уравнений. При этом в

соотношения могут входить переменные, относящиеся не только к текущему периоду t, но и к предшествующим

периодам. Такие переменные называются лаговыми. Переменные за предшествующие годы обычно выступают в

качестве объясняющих переменных.

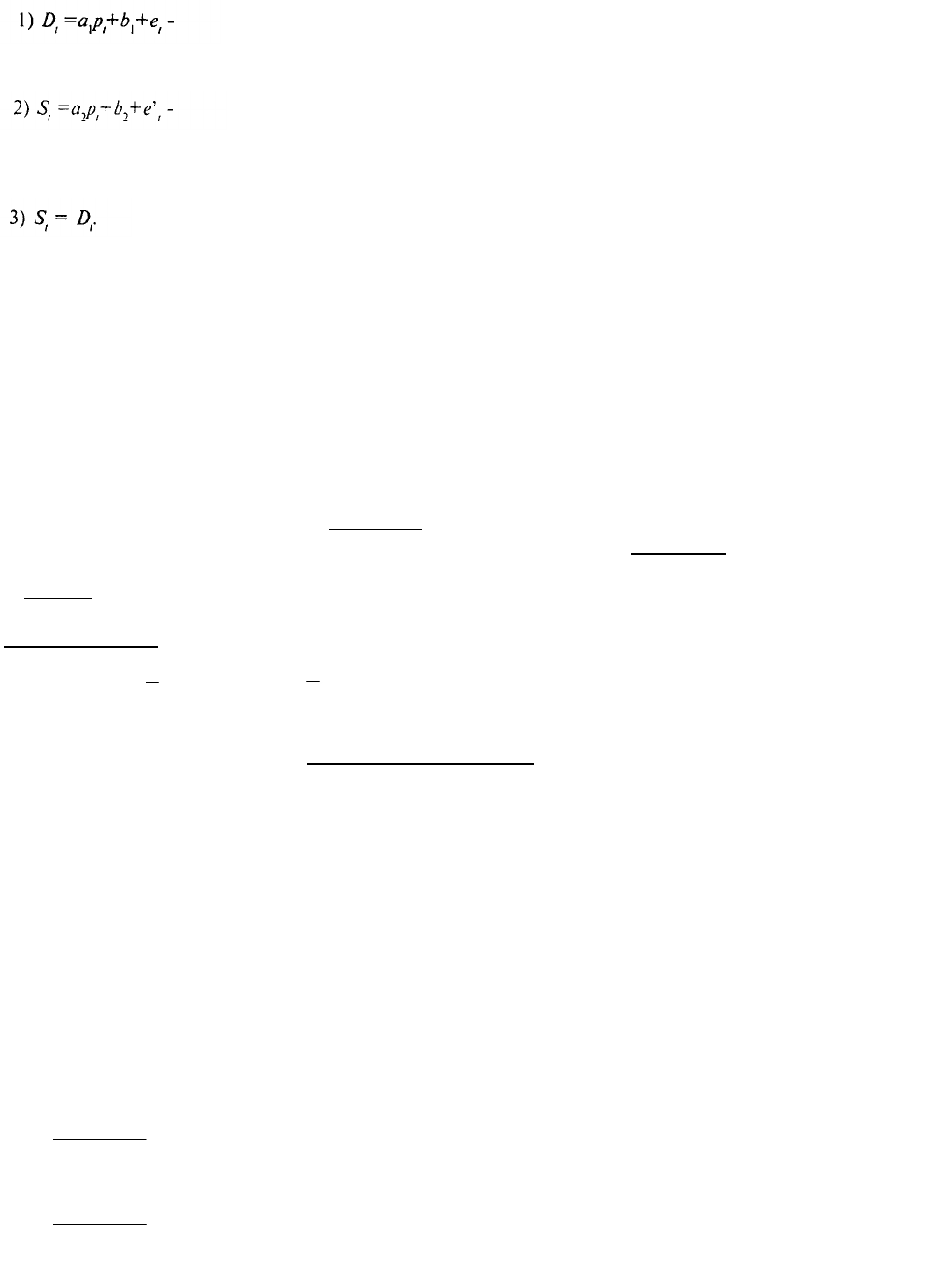
В качестве иллюстрации приведем пример из экономики. Рассмотрим модель спроса и предложения. Как известно,

спрос D на некоторый продукт зависит от его цены р. От этого же параметра, но с противоположным по знаку

коэффициентом, зависит и предложение этого продукта. Силы рыночного механизма формируют цену таким

образом, что спрос и предложение уравниваются. Нам нужно построить модель описанной ситуации. Для этого

имеются данные об уровне равновесных цен и спросе (который равен предложению). Представленную ситуацию

можно формализовать в виде следующей линейной модели:

(3.1)

спрос пропорционален цене с коэффициентом пропорциональности a1<0, т.е. связь отрицательная;

(3.2)

предложение пропорционально цене с коэффициентом пропорциональности а2>0, т.е. связь положительная;

(3.3)

Здесь еl, е'l\, (l=1,...,n) - ошибки модели, имеющие нулевое математическое ожидание.

Первые два из представленных уравнений, если их рассматривать отдельно, могут показаться вполне обычными. Мы

можем определить коэффициенты регрессии для каждого из этих уравнений. Но в этом случае остается открытым

вопрос о равенстве спроса и предложения, т.е. может не выполняться третье равенство, в котором спрос выступает в

качестве зависимой переменной. Поэтому расчет параметров отдельных уравнений в такой ситуации теряет смысл.

36. Структурная и приведенная формы модели.

Экономическая модель как система одновременных уравнений может быть представлена в структурной или в

приведенной форме. В структурной форме ее уравнения имеют исходный вид, отражая непосредственные связи между

переменными. Приведенная форма получается после решения модели относительно эндогенных (внутренних)

переменных, то есть выражения этих переменных только через экзогенные (задаваемые извне) переменные и параметры

модели. Структурная форма модели содержит эндогенные переменные –

. Это зависимые переменные, число которых

равно числу уравнений в системе, и (которые определяются внутри системы). Экзогенные переменные –

. Это

независимые переменные, которые определяются вне системы и влияющие на эндогенные переменные, но независящие

от них. Лаговые переменные – независимые переменные за предыдущие моменты времени. Лаговыми могут быть

эндогенные переменные за предшествующий период времени, и тогда они являются экзогенными.

Предопределённые переменные – это экзогенные и лаговые. Структурные коэффициенты модели:

 

при переменных x и y. Все переменные в модели выражены в отклонениях от среднего уровня, то есть под x

подразумеваются (

), под

– (

). Поэтому свободный член в каждом уравнении отсутствует.

Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории,

смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели

структурная форма модели преобразуется в приведенную форму модели:

xxxy

1212111





;

xxxy

2222121





; (4)

…

mnmnn

xxxy



 ..

2211

По своему виду приведённая форма модели идентична системе (1), поэтому параметры системы (4) оцениваются

традиционным МНК. А затем оценить значение эндогенных переменных через экзогенные.

Коэффициенты приведённой формы модели (4) представляют собой нелинейные функции коэффициентов

структурной формы модели. Пример простейшей структурной модели:

;

1112121

xayby 

2221212

xayby 

Приведенная форма получается так:

1111

xay





систему одновременных уравнений имеем

1111

xay





2221212

xayby 

Отсюда

22212121121111

xabybbxay 

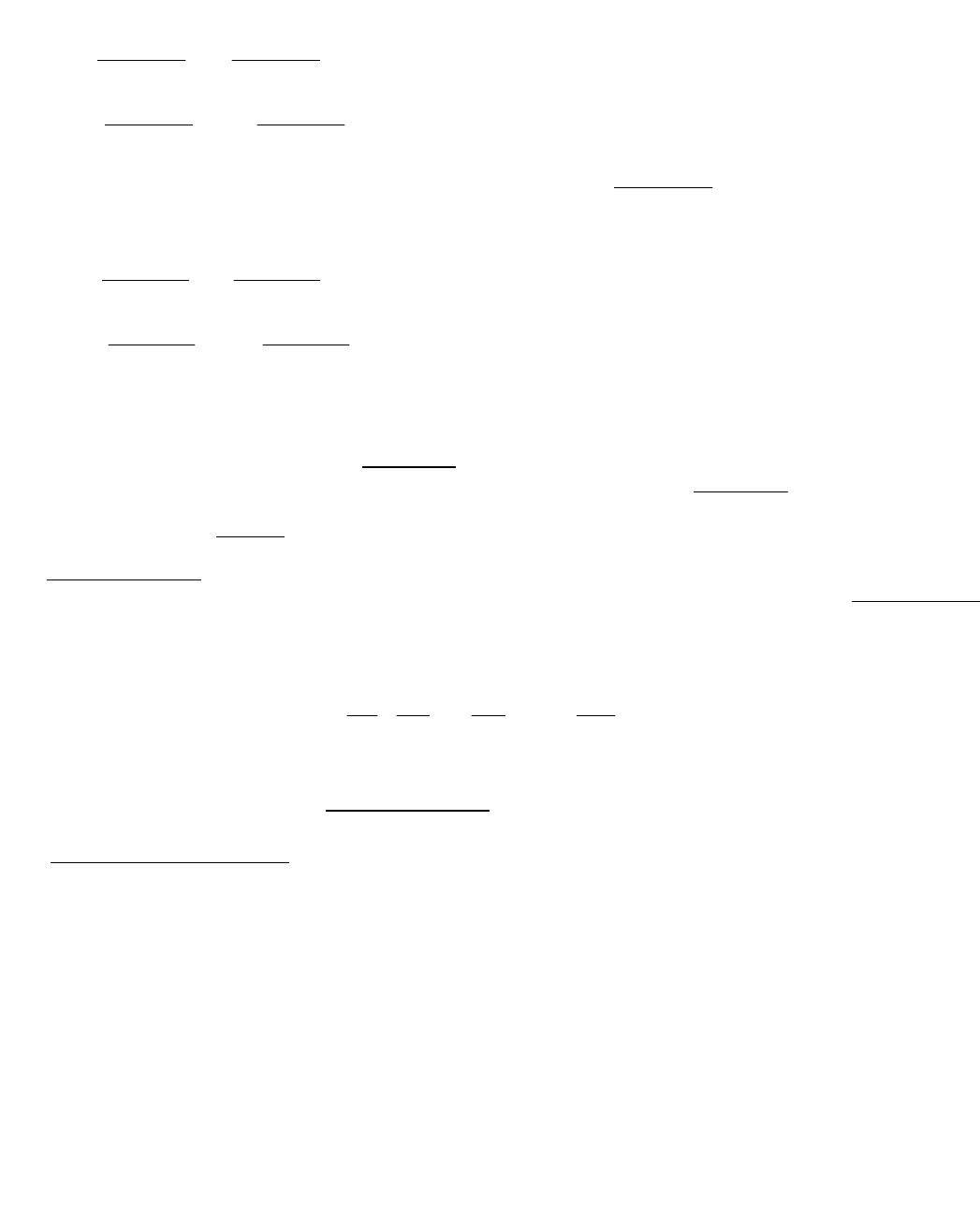
2221211121121

)1( xabxabby 

2112

2212

2112

2212

2112

;



















Аналогично, получается второе уравнение приведённой формы:

2222

xay





11121212212222

xabybbxay 

2112

2111

2112

2111

;



















37. Эндогенные и экзогенные переменные. Проблема идентифицируемости систем уравнений.

Структурная форма модели содержит эндогенные переменные –

. Это зависимые переменные, число которых

равно числу уравнений в системе, и (которые определяются внутри системы). Экзогенные переменные –

. Это

независимые переменные, которые определяются вне системы и влияющие на эндогенные переменные, но

независящие от них. Лаговые переменные – независимые переменные за предыдущие моменты времени. Лаговыми

могут быть эндогенные переменные за предшествующий период времени, и тогда они являются экзогенными.

Предопределённые переменные – это экзогенные и лаговые.

При переходе от приведённой формы модели к структурной возникает проблема идентификации. Идентификация

– это единственность соответствия между приведённой и структурной формами модели. Рассмотрим это на примере:

;...

12121112121 mm

xaxaxayby 

xaxaxayby

22221211212

...

. (5)

из второго уравнения следует:

..

Тогда в системе имеем два уравнения для эндогенной переменной y

c одним и тем же набором переменных, но с

разными коэффициентами. Наличие двух вариантов для расчёта структурных коэффициентов одной и той же модели

связано с неполной её идентификацией. Структурная модель в полном виде, состоящая в каждом уравнений системы из n

эндогенных и m экзогенных переменных, содержит

 

mnn  1

параметров.

Приведённая форма модели –

параметров, но

 

1n

, случай

=1 не

рассматриваем. Следовательно,

 

mnn  1

параметров структурной модели не могут быть однозначно определены из

параметров приведенной формы модели.

Чтобы получить единственно возможное решение для структурной модели, необходимо предположить, что

некоторые из структурных коэффициентов модели ввиду слабой взаимосвязи признаков с эндогенной переменной из

левой части системы, равны нулю. Тем самым уменьшится число коэффициентов структурной модели. Так, если

предположить, что в нашей системе

3m

a

то

;

2121112121

xaxayby 

;

3232221212

xaxayby 

(6)

тогда приведенная форма модели имеет вид:

313212111

xxxy





;

323222121

xxxy





и если в системе (5) при

=3 было 8 коэффициентов (

2322211312112112

,,,,,,, aaaaaabb

а в приведенной

только 6, то теперь в системе (6) 6 коэффициентов, и в приведённой 6, и тогда однозначность структурных

коэффициентов обеспечена.

Уменьшение числа структурные коэффициентов модели возможно и другими путями, например, приравнивания

некоторых коэффициентов друг другу, то есть путем предположений, что их взаимодействие на формируемую

эндогенную переменную одинаково.

С позиции идентифицируемости, модели можно разделить на 3 вида:

1. идентифицируемые;

2. неидентифицируемые;

3. сверхидентифицируемые.

Модель идентифицируема, если все структурные её коэффициенты определяются однозначно по коэффициентам

приведённой формы модели, то есть число параметров одной модели равно числу параметров другой.

Модель неидентифицируема, если число приведённых коэффициентов меньше числа структурных коэффициентов.

Структурная модель в полном виде

– эндогенных и

– экзогенных переменных, всегда неидентифицируема.

Модель сверхидентифицируема, если число приведённых коэффициентов больше числа структурных

коэффициентов.

В этом случае на основе коэффициентов приведённой формы можно получить более одного значения каждого

структурного коэффициента. В этом частном случае системы (6), если ещё и

a

, то система станет

сверхидентифицируемой.

;

2121112121

xaxayby 

;

3231212

xayby 

в ней 5 коэффициентов, а 6 коэффициентов приведённой формы.

Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически разрешима, но требует

для этого специальных методов вычисления параметров.

Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется

проверять на идентификацию.

Модель идентифицируема – если каждое уравнение системы идентифицируемо. Если хотя бы одно уравнение

неидентифицируемо, то и все модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя

бы одно сверхидентифицируемое уравнение.

Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение

было идентифицируемым, необходимо, чтобы число

– предопределённых переменных, отсутствующих в данном

уравнении, но присутствующих в системе, было равно числу

– эндогенных переменных в данном уравнении без

одного.

Для полной системы имеем nxm параметров приведённой системы и

 

mnn  1

параметров структурной

модели, поэтому в общем случае параметры структурной модели не могут быть однозначно определёнными через

параметры приведённой формы модели.

Для каждого уравнения системы имеем

– параметров приведённой формы,

 

mn  1

– параметров структурной модели;

Обозначим

– число экзогенных переменных, которые присутствуют в уравнении,

– число экзогенных переменных, которые отсутствуют в данном уравнении,

DDm 

;

Обозначим

– число эндогенных переменных в уравнении, тогда очевидно, чтобы решить поставленную задачу

определения параметров модели, необходимо потребовать, чтобы

HD

, в этом случае уравнение

идентифицируемо; если

 HD

, то уравнение неидентифицируемо; если

 HD

, то уравнение

сверхидентифицируемое.

Указанное условие отражает необходимое условие идентификации, но не достаточное. Достаточное условие

формируется с помощью ограничений на матрицу коэффициентов системы. Целесообразность проверки условия

идентификации модели через определитель матрицы коэффициентов при эндогенных и экзогенных переменных,

отсутствующих в данном уравнении, объясняется это тем, что возможна ситуация, когда для каждого уравнения

системы:

HD

, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается

лишь необходимое, но недостаточное условие идентифицируемости.

38. Оценивание параметров в системах одновременных уравнений: косвенный и

двухшаговый МНК.

Косвенный метод наименьших квадратов.

Процедура применения КМНК предполагает выполнение следующих этапов работ:

 структурная модель преобразовывается в приведенную форму модели;

 для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты (δ

);

 коэффициенты приведенной формы модели трансформируются в параметры структурной модели.

Пример:

Приведенная форма модели, построенной на основе имеющихся данных, имеет вид:









22221212

12121111

uxxy



где u

, u

- случайные ошибки приведенной формы модели

Для каждого уравнения приведенной формы модели применяет традиционный МНК и определяем δ-коэффициенты.

Для первого уровня приведенной формы модели система нормальных уравнений составит:















212211121

2112

11111

xxxxy



для второго уровня:















222212122

2122

12112

xxxxy



Переходим от приведенной к структурной форме модели:









22221212

11112121



xayby

Двухшаговый метод наименьших квадратов.

Основная идея ДМНК — на основе приведенной формы модели получить для сверхидентифицируемого уравнения

теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Далее, подставив их вместо

фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения.

Метод получил название двухшагового МНК, ибо дважды используется МНК: на первом шаге при определении

приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной:

=δ

+ δ

+…+ δ

и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении

структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.

Сверхидентифицируемая структурная модель может быть двух типов:

 все уравнения системы сверхидентифицируемы;

 система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.

Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения

используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним

находятся из системы приведенных уравнений.

Применим ДМНК к простейшей сверхидентифицируемой модели:

 









22221212

112121



xayby

xyby

Данная модель может быть получена из предыдущей идентифицируемой модели:









22221212

11112121



xayby

если наложить ограничения на ее параметры, а именно: b

В результате первое уравнение стало сверхидентифицируемым: Н=1 (у

), D=1(х

) и D+1 > Н. Второе уравнение не

изменилось и является точно идентифицируемым: Н = 2 и D=1

На первом шаге найдем приведенную форму модели, а именно:









22221212

12121111

uxxy



ДМНК является наиболее общим и широко распространенным методом решения системы одновременных уравнений.

Несмотря на важность системы эконометрических уравнений, на практике часто не принимают во внимание

некоторые взаимосвязи, применение традиционного МНК к одному или нескольким уравнениям также широко

распространено в эконометрике. В частности, при построении производственных функций анализ спроса можно вести,

используя обычный МНК.