Ответы на экзаменационные вопросы по курсу: Эконометрика
Подождите немного. Документ загружается.


где
òàáë
p p
y y
m t
, а
p
y
m
– средняя ошибка прогнозируемого индивидуального значения:
2
î ñò
2
1
1
p
p
y
x
x x
m S
n n
.
16. Коэффициент эластичности. Его смысл и определение.
Среди нелинейных моделей наиболее часто используется степенная функция
b
y a x
, которая приводится
к линейному виду логарифмированием:
Y A b X
,
где
ln , ln , ln , lnY y X x A a
. Т.е. МНК мы применяем для преобразованных данных:
2
,
,
A n b X Y
A X b X X Y
а затем потенцированием находим искомое уравнение.
Широкое использование степенной функции связано с тем, что параметр
b
в ней имеет четкое экономическое
истолкование – он является коэффициентом эластичности.
Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор
изменится на 1%. Формула для расчета коэффициента эластичности имеет вид:
x
Ý f x
y
. (1.19)
Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от
соответствующего значения фактора
x
, то обычно рассчитывается средний коэффициент эластичности:
x
Ý f x
y
. (1.20)
Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов
уравнений регрессии:
1.5Таблица
Вид функции,
y
Первая производная,
y
Средний коэффициент
эластичности,
Ý
Линеаризация
1 2 3
4
y a b x
b
b x
a b x
-
2
y a b x c x
2b c x
2
2b c x x
a b x c x
Х
1
=х, Х
2
=х
2
b
y a
x
2
b
x
b
a x b
Х=1/х,Y=y
b
y a x
1b
a b x
b
Х=lnх,Y=lny
x
y a b
ln
x
a b b
lnx b
Х=х,Y=lny
lny a b x
b
x
ln
b
a b x
Х=lnх,Y=y
a bx
y e
a bx
be
x b
Х=х,Y=lny
1 e
c x
a
y
b
2
e
1 e
c x
c x
a b c
b
e
c x
b c x
b
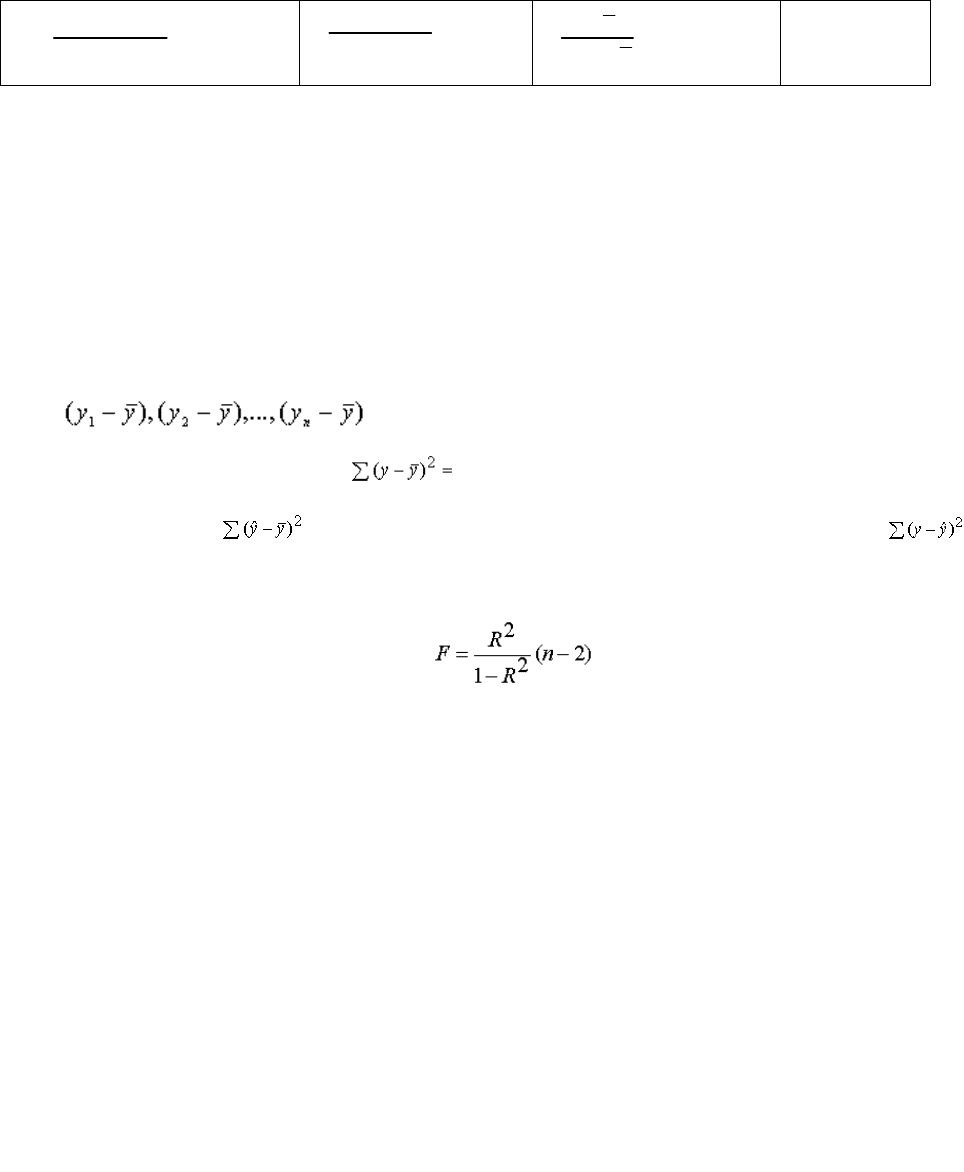
1
y
a b x
2
b
a b x
b x
a b x
Х=х,Y=1/y
17. Оценка статистической значимости уравнения в целом. F-критерий Фишера.
Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как
обусловленный влиянием фактора х, т. е. регрессией у по х, так и вызванный действием прочих причин
(необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть общей
вариации признака у приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений,
обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически
значимо и фактор х оказывает существенное воздействие на результат у. Это равносильно тому, что
коэффициент детерминации R
2
будет приближаться к единице.
Любая сумма квадратов отклонений связана с числом степеней свободы (df— degrees of freedom), т. е. с числом
свободы независимого варьирования признака. Число степеней свободы связано с числом единиц
совокупности N и с числом определяемых по ней констант. Применительно к исследуемой проблеме число
степеней свободы должно показать, сколько независимых отклонений из N возможных
требуется для образования данной суммы квадратов.
Так, для общей суммы квадратов требуется (n-1) независимых отклонений, ибо по совокупности из
n единиц после расчета среднего уровня варьируют лишь (n - 1) число отклонений. При расчете факторной
суммы квадратов - 1 степень свободы, и при расчете остаточной суммы квадратов - (n-2)
степени свободы.
Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F –
отношения (F - критерий):
JJJJ(8.1)
В качестве нулевой гипотезы Н
0
выдвигается предположение о том, что линейной зависимости между x и y не
существует.
Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н
0
необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз.
Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных
уровнях существенности нулевой гипотезы и различном числе степеней свободы.
Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место
при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение
F -отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае
нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи.
Если же величина окажется меньше табличной, то вероятность нулевой гипотезы выше заданного уровня
(например, 0,05) и она не может быть отклонена, без серьезного риска сделать неправильный вывод о наличии
связи. В этом случае уравнение регрессии считается статистически незначимым, Н
0
не отклоняется.
18. Модель множественной регрессии.
Множественная регрессия – уравнение связи с несколькими независимыми переменными:
),,...,,(
21 p
xxxfy
где
y
- зависимая переменная (результативный признак);
p
xxx ,...,,
21
- независимые переменные (факторы).
Линейная модель множественной регрессии имеет вид:
Y
i
= α
0
+ α
1
x
i1
+ α
2
x
i2
+ ... + α
m
x
im
+ ε
i
(4.1)
Коэффициент регрессии α
j
показывает, на какую величину в среднем изменится результативный признак Y, если
переменную x
j
увеличить на единицу измерения, т.е. α
j
является нормативным коэффициентом. Обычно
предполагается, что случайная величина ε
i
имеет нормальный закон распределения с математическим ожиданием
равным нулю и с дисперсией σ
2
.
Анализ уравнения (4.1) и методика определения параметров становятся более наглядными, а расчетные процедуры
существенно упрощаются, если воспользоваться матричной формой записи уравнения (4.2):
Y = X α + ε (4.2)
где Y — вектор зависимой переменной размерности n×1, представляющий собой n наблюдений значений y
j
,
X — матрица n наблюдений независимых переменных Х
1
, Х
2
, Х
3
, ..., Х
m
, размерность матрицы X равна n×(m+1);
α — подлежащий оцениванию вектор неизвестных параметров размерности (m+1) ×1;
ε — вектор случайных отклонений (возмущений) размерности n×1.

Таким образом,
Уравнение (4.1) содержит значения неизвестных параметров α
0
, α
1
, α
2
, ..., α
m
. Эти величины оцениваются на основе
выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют
собой лишь их статистические оценки. Модель линейной регрессии, в которой вместо истинных значений
параметров подставлены их оценки (а именно такие регрессии и применяются на практике), имеет вид:
, (4.3)
где α — вектор оценок параметров; е — вектор «оцененных» отклонений регрессии, остатки регрессии ε = Y - X α;
— оценка значений Y, равная Ха.
Для построения уравнения множественной регрессии чаще используются следующие функции:
линейная –
;...
2211
pp
xbxbxbay
степенная –
;...
21
21
p
b
p
bb
xxxay
экспонента –
;
...
2211
pp
xbxbxba
ey
гипербола -
pp
xbxbxba
y
...
1
2211
.
Можно использовать и другие функции, приводимые к линейному виду.
19. Ограничения модели множественной регрессии.
Предположим, что связь между объясняемой переменной
Y
и объясняющими переменными
mj
XXXX ,,,,,
21
линейная, т.е.
iimmijjiii
xbxbxbxbbY
22110
.
Пусть выполняются следующие условия:
1)
0
i
M
,
ni ,1
;
2)
2
ki
DD
, для любых
ki
;
3)
0,cov
ki
,
ki
,
4)
0,cov
iji
x
,
mj ,1
, т.е. распределение
i
не зависит от распределения любой объясняющей
переменной
j
X
;
5) ошибки
i
имеют нормальный закон распределения,
ni ,1
;
6)
nmXr 1
, т.е. ранг матрицы
X
должен быть равен числу оцениваемых параметров
1m
, что
означает отсутствие линейной зависимости между объясняющими переменными
m
XXX ,,,
21
.
Тогда МНК-оценка вектора
b
:
YXXXb
Ò
1
Ò
ÌÍÊ
ˆ
имеет наименьшую дисперсию в классе всех линейных
несмещенных и состоятельных оценок.
Условия Гаусса-Маркова 1)-6) называются предпосылками МНК для случая множественной линейной регрессии.
20. Идентификация параметров множественной регрессии МНК.
Возможны разные виды уравнений множественной регрессии: линейные и нелинейные.
Ввиду четкой интерпретации параметров наиболее широко используется линейная функция. В линейной
множественной регрессии
1 1 2 2
...
m m
x
y a b x b x b x
параметры при
x
называются коэффициентами
«чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на
единицу при неизмененном значении других факторов, закрепленных на среднем уровне.
Рассмотрим линейную модель множественной регрессии
1 1 2 2
...
m m
y a b x b x b x
. (2.1)

Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе
наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов
отклонений фактических значений результативного признака
y
от расчетных
y
минимальна:
2
min
i
i
x
i
y y
. (2.2)
Как известно из курса математического анализа, для того чтобы найти экстремум функции нескольких
переменных, надо вычислить частные производные первого порядка по каждому из параметров и приравнять их к нулю.
Итак. Имеем функцию
1m
аргумента:
2
1 2 1 1 2 2
, , , ..., ...
m m m
S a b b b y a b x b x b x
.
Находим частные производные первого порядка:
1 1 2 2
1 1 1 2 2
1
1 1 2 2
2 ... 0;
2 ... 0;
........................................................
2 ... 0.
m m
m m
m m m
m
S
y a b x b x b x
a
S
x y a b x b x b x
b
S
x y a b x b x b x
b
После элементарных преобразований приходим к системе линейных нормальных уравнений для нахождения
параметров линейного уравнения множественной регрессии (2.1):
1 1 2 2
2
1 1 1 2 1 2 1 1
2
1 1 2 2
... ,
... ,
................................................................
... .
m m
m m
m m m m m m
na b x b x b x y
a x b x b x x b x x yx
a x b x x b x x b x yx
(2.3)
Для двухфакторной модели данная система будет иметь вид:
1 1 2 2
2
1 1 1 2 1 2 1
2
2 1 1 2 2 2 2
,
,
.
na b x b x y
a x b x b x x yx
a x b x x b x yx
21. Интерпретация множественного уравнения регрессии.
Интерпретация моделей регрессии осуществляется методами той отрасли знаний, к которой относится исследуемое
явление. Но всякая интерпретация начинается со статистической оценки уравнения регрессии в целом и оценки
значимости входящих в модель факторных признаков.
Прежде всего необходимо рассмотреть коэффициенты регрессии. Чем больше величина коэффициента регрессии,
тем значительнее влияние данного признака на моделируемый.
Знаки коэффициентов регрессии говорят о характере влияния на результативный признак. Если факторный признак
имеет знак плюс, то с увеличением данного фактора результативный признак возрастает; если факторный признак
имеет знак минус, то с его увеличением результативный признак уменьшается.
Если экономическая теория подсказывает, что факторный признак должен иметь положительное значение, а он
имеет знак минус, то необходимо проверить расчеты параметров уравнения регрессии. Такое явление чаще всего
бывает в силу допущенных ошибок при решении. Однако следует иметь ввиду, что когда рассматривается
совокупное влияние факторов, то в силу наличия взаимосвязей между ними характер их влияния может меняться.
С целью расширения возможностей экономического анализа, используются частные коэффициенты эластичности,
определяемые по формуле: JJJJ(7.11)
где: - среднее значение соответствующего факторного признака; - среднее значение результативного признака;
a
1
- коэффициент регрессии при соответствующем факторном признаке.
Коэффициент эластичности показывает, на сколько процентов в среднем изменится значение результативного
признака при изменении факторного признака на 1%.
Частный коэффициент детерминации: JJJJ(7.12)
где: - парный коэффициент корреляции между результативным и i-ым факторным признаком;
- соответствующий стандартизованный коэффициент уравнения множественной регрессии: JJJJ(7.13)
Частный коэффициент детерминации показывает на сколько процентов вариация результативного признака
объясняется вариацией i-го признака, входящего в множественное уравнение регрессии.
Полная экономическая интерпретация моделей регрессии позволяет выявить резервы развития и повышения деловой
активности субъектов экономики.

22. Показатели тесноты связи во множественном регрессионном анализе - парные и частные
коэффициенты корреляции.
Корреля́ция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые
можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких
из этих величин приводят к систематическому изменению другой или других величин. Математической мерой
корреляции двух случайных величин служит коэффициент корреляции.
Корреляция может быть положительной и отрицательной (возможна также ситуация отсутствия статистической
взаимосвязи — например, для независимых случайных величин). Отрицательная корреляция — корреляция, при
которой увеличение одной переменной связано с уменьшением другой переменной, при этом коэффициент
корреляции отрицателен. Положительная корреляция — корреляция, при которой увеличение одной переменной
связано с увеличением другой переменной, при этом коэффициент корреляции положителен.
Величина влияния фактора на исследуемый отклик может быть оценена при помощи коэффициента линейной
парной корреляции, характеризующего тесноту (силу) линейной связи между двумя переменными.
Коэффициент можно определить по формуле:
.
(6.4)
Коэффициент обладает следующими свойствами:
1) не имеет размерности, следовательно, сопоставим для величин различных порядков;
2) изменяется в диапазоне от –1 до +1. Положительное значение свидетельствует о прямой линейной связи,
отрицательное – об обратной. Чем ближе абсолютное значение коэффициента к единице, тем теснее связь. Считается, что
связь достаточно сильная, если коэффициент по абсолютной величине превышает 0,7, и слабая, если он менее 0,3.
Значение коэффициента легко вычисляется при помощи MS Excel (функция КОРРЕЛ).
Величина r
2
называется коэффициентом детерминации. Он определяет долю вариации одной из переменных, которая
объясняется вариацией другой переменной.
Частный коэффициент корреляции - мера линейной связи между зависимой переменной Y и какой-либо одной из
переменных
k
x,...,x,x
10
после удаления влияния на эту связь всех остальных переменных
Укажем один из способов построения частного коэффициента корреляции. Пусть, например, изучается линейная
связь между переменными
y,x,x
21
и требуется найти коэффициент корреляции между зависимой переменной
y
и
независимой переменной
1
x
, «очищенный» от влияния переменной
2
x
.
Вычислим парные коэффициенты корреляции
2121
xxyxyx
r,r,r
и рассмотрим разность
2121
xxyxyx
rrr
(3.29)
Если переменные
y
и
1
x
не коррелируют с
2
x
, то
1
yx
r
.Оценивать зависимость с помощью разности (3.29)
неудобно. Поэтому ее нормируют так, чтобы получившийся коэффициент был в пределах от –J1 до +J1. В этом случае
получаем выражение
22
212
2121
21
11
xxyx
xxyxyx
xyx
rr
rrr
r
. (3.30)
Величина
21
xyx
r
называется частным коэффициентом корреляции величин
y
и
1
x
без учета влияния
2
x
. Если
требуется устранить влияние на
y
двух переменных
2
x
и
3
x
, то по формуле (3.30) вычислим предварительно
коэффициенты
21
xyx
r
,
23
xyx
r
,
231
xxyx
r
. Затем вычисляем коэффициент
22
23123
2312321
321
11
xxxxyx
xxxxyxxyx
xxyx
rr
rrr
r
,
(3.31)
который отражает зависимость между
y
и
1
x
без учета влияния
2
x
и
3
x
. Аналогично поступают в случае
любого числа переменных. Можно показать, что коэффициент частной корреляции показывает тесноту связи
результирующего признака с одним из факторов при неизменном уровне других факторов.
Частные коэффициенты корреляции имеют те же свойства, что и обычные. При выборе наилучшей модели с их
помощью определяют, какая переменная оказывает на переменную выхода наибольшее влияние.
23. Стандартизированное уравнение множественной регрессии.
Другой вид уравнения множественной регрессии – уравнение регрессии в стандартизированном масштабе:
,...
21
21
tttt
xxx
p
p
y
где
x
xx
x
yy
i
i
ii
y
y
tt
,
- стандартизированные переменные;

i
- стандартизированные коэффициенты регрессии.
К уравнению множественной регрессии в стандартизированном масштабе применим МНК. Стандартизированные
коэффициенты регрессии (
- коэффициенты) определяются из следующей системы уравнений:
....
..................................................................................
,...
,...
321
22312
2
11312
1
321
321
321
p
xxxxxx
xx
p
xxxx
xx
p
xxxx
rrrr
rrrr
rrrr
yx
yx
yx
.Связь коэффициентов множественной регрессии
b
i
со стандартизированными
коэффициентами
i
описывается соотношением
.
x
y
i
i
b
Параметр
a
определяется как
xbxb
xb
ya
pp
...
11
22
.
Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле
.
y
yx
x
bЭ
j
j
j
Для расчета частных коэффициентов эластичности применяется следующая формула:
y
x
bЭ
xxxxxx
i
i
iii
i
y
,...,,,...,,
1121
.
24. Коэффициент множественной корреляции, скорректированный коэффициент
множественной корреляции, множественный коэффициент детерминации.
Экономические явления чаще всего адекватно описываются именно многофакторными моделями. Поэтому
возникает необходимость обобщить рассмотренное выше корреляционное отношение (6.4) на случай нескольких
переменных.
Теснота линейной взаимосвязи между переменной y и рядом переменных x
j
, рассматриваемых в целом, может быть
определена с помощью коэффициента множественной корреляции.
Предположим, что переменная y испытывает влияние двух переменных - x и z. В этом случае коэффициент
множественной корреляции может быть определен по формуле:
.
(6.9)
где r
yx
, r
yz
, r
xz
- простые коэффициенты линейной парной корреляции, определенные из соотношения (6.4).
Коэффициент множественной корреляции заключен в пределах 0 ≤ R ≤ 1. Он не меньше, чем абсолютная величина
любого парного или частного коэффициента корреляции с таким же первичным индексом.
С помощью множественного коэффициента (по мере приближения R к 1) делается вывод о тесноте взаимосвязи, но
не о ее направлении. Величина R
2
, называемая множественным коэффициентом детерминации, показывает,
какую долю вариации исследуемой переменной (y) объясняет вариация остальных учтенных переменных (x, z).
Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и
рассчитывается по формуле:
,
)1(
)1(
)1(1
ˆ
22
mn
n
RR
где n-число наблюдений; m – число факторов.
25. Оценка статистической значимости множественных коэффициентов регрессии, t-
критерий Стьюдента.
Оценка значимости коэффициентов чистой регрессии с помощью t-критерия Стьюдента сводится к вычислению
значения
.
i
i
i
x
b
i
b
F
m
b
t
где
i
b
m
- средняя квадратичная ошибка коэффициента регрессии
,i
b
она может быть определена по следующей
формуле:
.
1
1
.
1
1
2
2
1
1
mn
R
R
m
pii
p
i
xxxx
xyxy
b
26. Модели с переменной структурой (фиктивные переменные).

До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные
значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий
два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как
профессия, пол, образование, климатические условия, принадлежность к определенному региону. Чтобы ввести
такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т.е.
качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в
эконометрике принято называть фиктивными переменными.
Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского
и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности
обследуемых уравнение регрессии имеет вид:
y a bx
, где y – количество потребляемого кофе; x– цена.
Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола:
1 1 1 1 1
y a b x
и женского пола:
2 2 2 2 2
y a b x
.
Различия в потреблении кофе проявятся в различии средних
1
y
и
2
y
. Вместе с тем сила влияния
x
на
y
может
быть одинаковой, т.е.
1 2
b b b
. В этом случае возможно построение общего уравнения регрессии с включением в
него фактора «пол» в виде фиктивной переменной. Объединяя уравнения
1
y
и
2
y
и, вводя фиктивные переменные,
можно прийти к следующему выражению:
1 1 2 2
y a z a z bx
, где
1
z
и
2
z
– фиктивные переменные, принимающие значения:
1
1 мужской пол,
0 женский пол;
z
2
0 мужской пол,
1 женский пол.
z
Предположим, что определено уравнение
1 1
y A A z bx
, где
1
z
принимает значения 1 для мужчин и
0 для женщин.
Теоретические значения размера потребления кофе для мужчин будут получены из уравнения
1
y A A bx
.
В отд. случаях необходимо введение двух и более групп фиктивных переменных, т.е. двух и более качественных
факторов, каждый из которых может иметь несколько градаций. Например, при изучении потребления некоторого товара
наряду с факторами, имеющими количественное выражение (цена, доход на одного члена семьи, цена на
взаимозаменяемые товары и др.), учитываются и качественные факторы. С их помощью оцениваются различия в
потреблении отдельных социальных групп населения, дифференциация в потреблении по полу, национальному составу и
др. При построении такой модели из каждой группы фиктивных переменных следует исключить по одной переменной.
Так, если модель будет включать три социальные группы, три возрастные категории и ряд экономических переменных,
то она примет вид:
1 1 2 2 3 1 4 2 5 1 6 2 4
...
m m
y a b s b s b z b z b x b x b x
, где y – потребление;
1 2
, , ...,
m
x x x
– экономические
(количественные) переменные.
1 если наблюдения относятся к -й социальной группе 1, 2 ,
0 в остальных случаях;
i
i i
s
1 если наблюдения относятся к -й возрастной группе 1, 2 ,
0 в остальных случаях;
i
j j
z
До сих пор мы рассматривали фиктивные переменные как факторы, которые используются в регрессионной
модели наряду с количественными переменными. Вместе с тем возможна регрессия только на фиктивных переменных.
Н-р, изучается дифференциация з/платы рабочих высокой квалификации по регионам страны. Модель з/платы может
иметь вид:
1 1 2 2
...
m m
y a b z b z b z
, где y – ср.з/плата рабочих высокой квалификации по отдельным предприятиям;
1
1 если предприятие находится в Северо-Западном районе;
0 если предприятие находится в остальных районах;
z
2
1 если предприятие находится в Волго-Вятском районе;
0 если предприятие находится в остальных районах;
z
………………………………………………………………………..
1 если преприятие находится в Дальневосточном районе;
0 если предприятие находится в остальных районах.
m
z
Поскольку последний район, указанный в модели, обозначен
m
z
, то в исследование включено
1m
район.
Мы рассмотрели модели с фиктивными переменными, в которых последние выступают факторами. Может
возникнуть необходимость построить модель, в которой дихотомический признак, т.е. признак, который может
принимать только два значения, играет роль результата, например, при обработке данных социологических опросов. В
качестве зависимой переменной
y
рассматриваются ответы на вопросы, данные в альтернативной форме: «да» или
«нет». Поэтому зависимая переменная имеет два значения: 1, когда имеет место ответ «да», и 0 – во всех остальных
случаях. Модель такой зависимой переменной имеет вид:
1 1
...
m m
y a b x b x
.
Модель является вероятностной линейной моделью. В ней y принимает значения 1 и 0, которым соответствуют
вероятности
p
и
1 p
. Поэтому при решении модели находят оценку условной вероятности события
y
при
фиксированных значениях
x
.

27. Оценка статистической значимости множественного уравнения регрессии, F-критерий
Фишера.
Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера:
.
1
1
2
2
m
mn
R
R
F
Частный F-критерий оценивает статистическую значимость присутствия каждого факторов в уравнении. В общем
виде для фактора
i
x
частный F-критерий определится как
.
1
1
1
2
22
1
1111
mn
R
RR
F
pI
piipi
i
x
xxyx
xxxyxxxyx
част
28. Спецификация модели множественной регрессии. Свойства множественных
коэффициентов регрессии.
Суть регрессионного анализа: построение математической модели и определение ее статистической надежности.
Вид множественной линейной модели регрессионного анализа:
Y = b
0
+ b
1
x
i1
+ ... + b
j
x
ij
+ ... + b
k
x
ik
+ e
i
где e
i
- случайные ошибки наблюдения, независимые между собой, имеют нулевую среднюю и дисперсию s.
Назначение множественной регрессии: анализ связи между несколькими независимыми переменными и зависимой
переменной.
Экономический смысл параметров множественной регрессии
Коэффициент множественной регрессии b
j
показывает, на какую величину в среднем изменится результативный признак
Y, если переменную X
j
увеличить на единицу измерения, т. е. является нормативным коэффициентом.
Матричная запись множественной линейной модели регрессионного анализа:
Y = Xb + e
где Y - случайный вектор - столбец размерности (n x 1) наблюдаемых значений результативного признака (y
1
, y
2
,..., y
n
);
X - матрица размерности [n x (k+1)] наблюдаемых значений аргументов;
b - вектор - столбец размерности [(k+1) x 1] неизвестных, подлежащих оценке параметров (коэффициентов регрессии)
модели;
e - случайный вектор - столбец размерности (n x 1) ошибок наблюдений (остатков).
На практике рекомендуется, чтобы n превышало k не менее, чем в три раза.
Задачи регрессионного анализа
Основная задача регрессионного анализа заключается в нахождении по выборке объемом n оценки неизвестных
коэффициентов регрессии b
0
, b
1
,..., b
k
. Задачи регрессионного анализа состоят в том, чтобы по имеющимся
статистическим данным для переменных X
i
и Y:
получить наилучшие оценки неизвестных параметров b
0
, b
1
,..., b
k
;
проверить статистические гипотезы о параметрах модели;
проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели
данным наблюдений).
Построение моделей множественной регрессии состоит из следующих этапов:
1. выбор формы связи (уравнения регрессии);
2. определение параметров выбранного уравнения;
3. анализ качества уравнения и поверка адекватности уравнения эмпирическим данным, совершенствование
уравнения.
Множественная регрессия:
Множественная регрессия с одной переменной
Множественная регрессия с двумя переменными
Множественная регрессия с тремя переменными
29. Решение проблемы выбора модели (с ограничением и без ограничения).
30. Методы отбора факторов: априорный и апостериорный подходы.
“Оптимальный” состав факторов, вкл в эконом модель, явл одним из основных условий ее “хорошего” качества,
понимаемого и как соответствие формы модели теор концепции, выражающей содержание взаимосвязей между
рассматриваемыми переменными, и как точность предсказания на рассматриваемом интервале времени t=1Можно
выделить два основных подхода к решению этой проблемы
Априорный подход к отбору Метод вкл. в модель переменных(до построения модели) с помощью него проводится
исследование характера и силы взаимосвязей между расс-ми переменными, по результатам к-го в модель вкл.факторы
наиболее значимые по своему непосредственному влиянию на зависимую переменную Y. Степень влияния оценивает
выборочный коэф-т корреляции rxy Считается что при [r]>0.7 установленную зависимость целесообразно исп-ть в
анализе планировании, прогнозировании и в решении др.практических вопросов.Рассматриваемые факторы не должны
сильнокорр-ть степень тесноты связи между ними опред. Как rxy=∑(xi-xiср)(xj-xjср)/корень∑(xi-xiср)2(xj-xjср)2 i≠j На
практике взаимосвязь между факторами признается сущ-ой если [rxy]>0.7, если они выражают одно и тоже явление, то

один из факторов следует искл. Чтобы одна и таже причина не учитывалась дважды в модели. В модель вкл. те факторы
к-ые боле сильно связаны с др.факторами. При наличии сильной колениарности фактороврекомендуется искл.тот фактор,
теснота парной зависимости к-ого меньше тесноты межфакторной связи. Для опред. Вкл. расс-ых переменных в модель
или их невкл. Часто используется таблица (матрица) составленная из коэф-тов парной кор-ции.
Апостериорный подход к отбору факторов Метод искл. из модели переменных. Предполагает первоначально
вкл. в модель все отобранные на этапе содержательного анализа факторы и на основе анализа хар-к качества
построеноой модели отбирать состав факторов. Одну из групп явл. Хар-ки выр-щие силу влияния каждого из
факторов на зависимую переменную У,т.е. силу влияния оценок параметров b1,b2,…,bm построенной
моделиОкончательное решение о вкл.или искл.принимается на основе анализа всего комплекса ее харак-тик
качества с учетом содержательной стороны проблемы взаимосвязей между зависимой и независимой
переменными.
31. Гетероскедастичность и автокорреляция случайного члена.
Одним из предположений теории наименьших квадратов является предположение, что все
ошибки
i
наблюдений имеют одинаковые дисперсии. Однако, при моделировании реальных
экономических процессов это предположение выполняется далеко не всегда. Посмотрим на ряд
урожайностей зерновых в США на рис. 4.1. Можно предположить, что с начала 20 века, с
повышением уровня агротехники, индустриализацией и химизацией сельского хозяйства росла не
только средняя урожайность, но и абсолютные колебания урожаев вокруг среднего уровня. Если
описать изменения среднего уровня урожайности некоторым уравнением регрессии, то ошибки
наблюдений будут возрастать с течением времени.
Предположение о том, что ошибки
i
наблюдений имеют одинаковые дисперсии, называется
гомоскедастичностью. Если же ошибки
i
наблюдений имеют разные дисперсии, то говорят о
гетероскедастичности наблюдений.
во многих случаях обнаружение гетероскедастичности визуально не столь очевидно. Чтобы определить, присутствует
ли гетероскедастичность на самом деле, применяют различные тесты.
Все тесты основаны на предположении о наличии связи между дисперсиями остатков моделей и объясняющими
переменными или расчетными значениями зависимой переменной в случае гетероскедастичности.
Эта связь обнаруживается с помощью коэффициента ранговой корреляции в тесте ранговой корреляции Спирмена,
либо предполагается пропорциональность стандартных отклонений
)(
i
и зависимой переменной Y в тесте
Голдфелда-Квандта, либо строятся различные линейные и нелинейные регрессии
i
,
i
2
,
i
на объясняющие
переменные или степени зависимой переменной Y и проверяется значимость полученных коэффициентов регрессии в
тесте Уайта.
Подходы к решению проблемы гетероскедастичности
1-й общий подход к решению данной проблемы состоит в преобразовании исходных данных таким образом, чтобы
для преобразованных данных модель уже обладала свойством гомоскедастичности. Применяют чаще всего два вида
преобразований а) логарифмирование данных; б) переход к безразмерным величинам путем деления на некоторые
известные величины, той же размерности, что и исходные данные. Возможна также стандартизация исходных данных.
Второй подход состоит в применении взвешенного и обобщенного метода наименьших квадратов.
Вычитая из данных X(t
i
) выровненные значения
)t(X
i
, получаем остатки, случайную составляющую тренда
(t) =X(t) -
)t(X
i
. (5.14)
Обычно считается, что выравнивание удовлетворительное, если остатки
(t) образуют стационарный процесс с
нулевым математическим ожиданием m
(t) = M[
(t)] = 0.
Кроме того, для корректного применения МНК, необходимо более жесткое предположение, что
(t) – случайные
независимые (хотя бы некоррелированные) величины с m
(t) = 0. Если же
(t
i
) коррелируют между собой, то говорят,
что в модели присутствует автокорреляция остатков. Метод наименьших квадратов и в этом случае дает несмещенные
и состоятельные оценки коэффициентов уравнений кривых.
Однако, получаемые при этом стандартные ошибки и доверительные интервалы для коэффициентов оказываются
заниженными.
Это может привести к ошибочным выводам при оценке качества отобранной модели поведения временного ряда.
Значительная корреляция остатков сигнализирует о том, что, либо кривая
)t(X
подобрана неудачно, либо придется
строить еще одну модель для описания поведения самих остатков
(t
i
).
Итак, при анализе модели тренда необходимо определить присутствует или нет автокорреляция в
(t
i
).
Предварительную оценку случайности поведения остатков проводят на основе критерия поворотных точек. В
соответствии с ним каждое значение
(t
i
) ряда остатков сравнивается с двумя рядом стоящими значениями
(t
i
– 1) и
(t
i
+
1).
Если
(t
i
) >
(t
i–1
) и
(t
i
) >
(t
i+1
) или
(t
i
) <
(t
i–1
),
(t
i
) <
(t
i+1
), то точка
(t
i
) считается поворотной (в ней достигается
локальный максимум или минимум). Далее подсчитывается общее количество поворотных точек P. В случайном ряду
остатков должно выполнятся строгое неравенство:
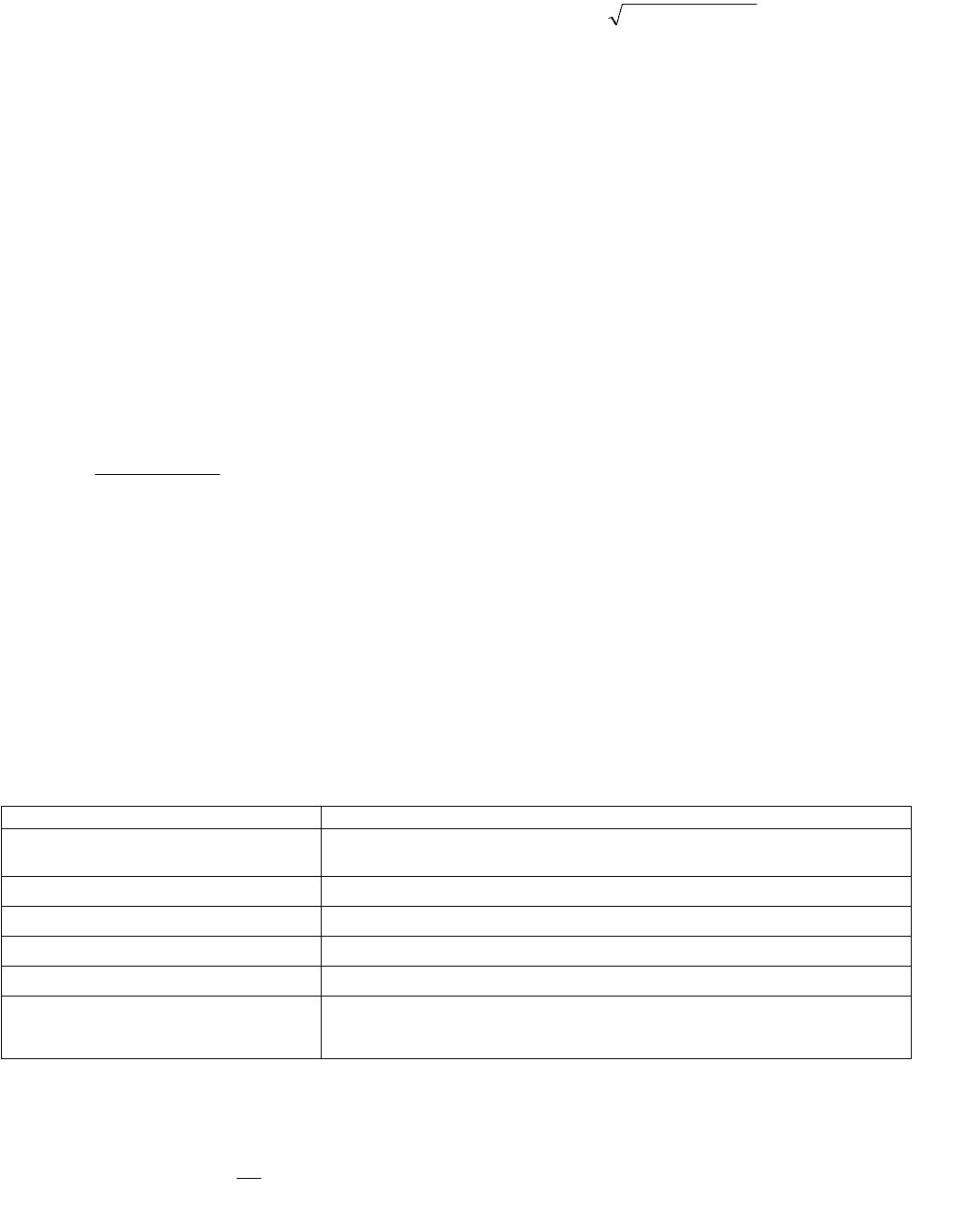
P > [2(n – 2)/3 – 2
]90/)2916( n
. (5.15)
Квадратные скобки здесь означают, что берется целая часть числа (не путать с процедурой округления). Отметим,
что критерий поворотных точек сигнализирует только о наличии положительной корреляции в ряде остатков. Если число
поворотных точек P велико, приближается к nC–C2 , то можно говорить о наличии отрицательной корреляции между
соседними членами временного ряда остатков. Критерий поворотных точек является предварительным и его следует
дополнить другими, более точными критериями.
32. Автокорреляция 1-го порядка и критерий Дарбина-Уотсона.
В классической регрессионной модели выполнение третьего условия Гаусса-Маркова (Соv(ε
t
ε
S
) = 0,при t ≠ s)
гарантирует некоррелированность значений случайных членов в различные моменты наблюдений и это позволяет
получить несмещенные МНК-оценки с минимальной дисперсией. Зависимость значений случайных членов в различные
моменты времени называется автокорреляцией (сериальной корреляцией).
Формальной причиной автокорреляции в регрессионных моделях является нарушение третьего условия теоремы
Гаусса-Маркова, действительной же причиной может быть: неправильная спецификация переменных (пропуск важной
объясняющей переменной); использование ошибочной функциональной зависимости, а иногда и характер наблюдений
(например, временные ряды).
Для проверки на автокорреляцию используется ряд критериев, из которых наиболее широкое применение получил
критерий Дарбина-Уотсона:
n
t
t
n
t
tt
e
ee
DW
1
2
2
2
1
Критерий DW связан с выборочным коэффициентом корреляции между е
t
и е
t-1
, соотношением: DW≈2(1-r),
Если автокорреляция отсутствует, то DW ≈ 2, при наличии положительной автокорреляции DW<2, если
автокорреляция отрицательна, DW>2. И поскольку коэффициент корреляции принимает значения -1 ≤ r ≤ 1, то 0≤ DW ≤
4. Полученное для данной регрессии значение статистики сравнивается с верхней и нижней границами ее критического
значения d
L
≤ d
крит
≤d
U
. Границы d
U
и d
L
выбираются из таблиц по числу наблюдений n, числу регрессоров k и уровню
значимости α. При этом возможны следующие случаи:
1. Наличие положительной автокорреляции: DW<d
L
.
2. Наличие отрицательной автокорреляции: DW >4-d
L
.
3. Автокорреляция отсутствует: d
U
≤ DW≤ 4-d
U
.
4. Зоны неопределенности: d
L
<DW< d
U
или 4- d
U
<DW<4-d
L
.
Этот тест подробно исследован и реализован во всех статистических пакетах, STATGRAPHICS, STATISTICA и
других.
Значение статистики DW Вывод
4 – d
l
< DW < 4
Гипотеза о независимости остатков отвергается, есть отрицательная
корреляция
4 – d
u
< DW < 4 – d
l
Неопределенность
2 < DW < 4 – d
u
Принимается гипотеза о независимости остатков
d
u
< DW < 2 Принимается гипотеза о независимости остатков
d
l
< DW <d
u
Неопределенность
0 < DW <d
l
Гипотеза о независимости остатков отвергается, есть положительная
корреляция
33. Тест серий (критерий Бреуша-Годфри)
Тест основан на следующей идее: если имеется корреляция между соседними наблюдениями, то естественно
ожидать, что в уравнении
,,1,
1
niee
iii
(*)
где e
i
– остатки регрессии, получаемые обычным МНК, коэффициент
окажется значимо отличающимся от нуля.
Практическое применение теста заключается в оценивании МНК регрессии (*), где временной ряд e
i-1
представляет
ряд e
i
со сдвигом по времени на единицу.
Преимущество теста Б-Г по сравнению с тестом Д-У заключается в том, что он проверяет с помощью
статистического критерия, между тем как тест Д-У содержит зону неопределенности для значений d – статистики.
Другим преимуществом теста является возможность обобщения: в число регрессоров могут быть включены не
только остатки с лагом 1, но и с лагом 2, 3 и так далее, что позволяет выявить корреляцию не только между
соседними, но и между более отдаленными наблюдениями.
34. Тесты на гетероскедастичность: Голдфелда-Квандта, тест Уайта.
