Ответы на экзамен (2 семестр)
Подождите немного. Документ загружается.


1
Консервативные и неконсервативные силы.
Сила F, действующая на матерьяльную точку называется консервативной или
потенциальной, если работа этой силы по перемещению этого тела из состояния 1
в состояние 2 не зависит от формы траектории движения, а зависит только от
начального и конечного положения тела. Для консервативной или потенциальной
силы работа по перемещению тела по замкнутой траектории равна нулю.
A = (интеграл с кружком в центре) Fdt=0 – условие потенциальной силы.
В противном случае сила называется диссепативной. Дессипативная сила
зависит от скорости точек и совершает отрицательную работу.
N = dA / dt – мгновенная мощность
. Полной энергией называется сумма кинетической и потенциальной энергий.
Механическая система называется консервативной, если все приложенные к ней
непотенциальные силы не совершают работу, а все потенциальные силы
постоянны во времени. Потенциальная энергия системы может изменяться
только за счет изменения ее консервации, поэтому если конфигурация
системы не меняется, то Wп = const
дWп / dt = 0. Рассмотрим консервативную систему, на которую действует
внутренняя и внешняя консервативные силы и внешние диссепативные силы.
Пусть вектор Fi – это внешняя консервативная сила, приложенная к внешней
точке. Вектор Fi’ – внутренняя консервативная сила. Вектор f i – внешняя
диссепативная сила. Запишем 2ой закон Ньютона для i-той точки матерьяльной
системы: m i * dv i / dt = Fi + Fi’ + f i ; dr = v i * dt ;
mi vi dt * dv / dt = (Fi’ + Fi) dvi + fi dri ; d (mi vi [ст.2] / 2) = (Fi’+Fi)dri+fidri
Для всей системы будет тоже самое, но ставится знак суммы перед каждым
слагаемым. Отсюда следует dWk + dWп = dA ; d(Wk + Wп) = dA ;
A1-2 = (интеграл 1-2) d(Wk + Wп) ; A1-2 = (Wk + Wп)2 = - (Wk - Wп)1.
Если внешние силы не совершают работу, то dA=0 ; d (Wk + Wп) = 0 ;
т.е. полная энергия системы остается постоянной Wk + Wп = const
2
Свободные и затухающие колебания. Во всякой реальной колебательной системе
всегда присутствует сила трения, которую также необходимо учитывать при
рассмотрении колебания. При колебательном движении осциллятора им будет
совершена работа против сил трения, в результате чего энергия колебаний будет
постепенно уменьшаться и как следствие будет уменьшаться амплитуда
колебаний. Свободные затухающие колебания – это колебания, амплитуда
которых с течением времени уменьшается из-за потерь энергии колебательной
системой. Рассмотрим линейную колебательную систему – систему, параметры
которой не изменяются в ходе колебаний. Рассмотрим колебания осциллятора, на
который помимо квазе-упругих сил действует сила трения. Будем считать, что эта
сила трения пропорциональна скорости колебания матерьяльной точки.
F= Fупр+Fтр ; Fупр = -kx ; Fтр = -b * dx/dt ; m * d2 x / dt (ст.2)= -b*dx/dt – kx
Уравнение, описывающее затухающие колебания:
(d2 x / dt (ст2)) + b/m * dx/dt + kx / m = 0 ; Введем обозначения:
w 0 (ст.2) = k/m ; b/m = 2БЕТА ; БЕТА = b/2m; b – коэффициент сопротивления ;
(d2 x / dt (ст.2)) + 2БЕТА*dx/dt + w 0 (ст.2) x = 0 ;
БЕТА – коэффициент затухания.
Общее решение этого уравнения будем искать в виде X = A e (ст.ЛЯМДА t).
Подставим это решение в дифференциальное уравнение затухающих колебаний:
dx/dt = A ЛЯМДА e (ст. ЛЯМДА t) ; d2 x / dt (ст.2) = A ЛЯМДА (ст.2) e (ст.
ЛЯМДА t); A ЛЯМДА (ст.2) e (ст. ЛЯМДА t) + 2bA ЛЯМДА e (ст.ЛЯМДА t) + w 0
(ст.2) A e (ст.ЛЯМДА t) ; Сокращаем:
ЛЯМДА (ст.2) +2БЕТА d + w 0 (ст.2) = 0 – характеристическое уравнение.
Решая его, получаем: X = - БЕТА + - (корень БЕТА (ст.2) – w 0 (ст.2)) =
- БЕТА + - i (корень w 0 (ст.2) – БЕТА (ст.2)) ; Таким образом общее решение
исходного дифференциального уравнения можно преобразовать к виду: w =
(корень w 0 (ст.2) – БЕТА (ст.2)) ; X (t) = A0 e (ст. – БЕТА t) sin (wt + φ 0) ;
(рисунок – график затухающих колебаний – сжатый синус, все ниже и неже стает
по оси OY).
Затухающие колебания не являются периодическими, т.к. максимальное значение
колеблющихся величин, достигаемое в некоторый момент времени в последующем
никогда не повторяется, поэтому можно говорить об условном периоде
затухающих колебаний – T = 2ПИ / w = 2ПИ / (корень w 0 (ст.2) – БЕТА (ст.2)).
Если БЕТА >= w 0, то процесс становится апериодическим.
совершаемой самой системой.
Первое начало термодинамики или первый закон термодинамики.
dQ = dU + dA ; Теплота, подводимая к термодинамической системе идет на
изменение внутренней энергии и на совершение работы.
Внутренняя энергия U определяется только состоянием термодинамической
системы, а Q и A являются характеристиками процесса при котором система
переходит из одного состояния в другое. Переход системы из одного состояния в
другое может осуществляться различными путями, поэтому Q и A зависят от
способа перехода системы из одного состояния в другое, в то время, как
внутренняя энергия U определяется только состоянием системы и не зависит от
того, каким путем система перешла в это состояние.
3
Реальные газы. При движении молекулы вдали от стенок сосуда, в
котором заключен газ, на нее действуют силы притяжения соседних
молекул, но равнодействующая всех этих сил в среднем равна нулю, т.к.
молекулу со всех сторон окружает в среднем одинаковое число соседей.
При приближении некоторой молекулы к стенке сосуда все остальные
молекулы газа оказываются по одну сторону от нее и равнодействующая
всех сил притяжения оказывается направленной от стенки сосуда внутрь
газа. Это приводит к тому, что уменьшается импульс, передаваемый
молекулой стенке сосуда. В результате давление газа на стенки сосуда
уменьшается по сравнению с тем, каким оно было бы в отсутствие сил
притяжения между молекулами: p = p идеального + delta p. Вместо
уравнения идеального газа получаем p + delta p = nkT ; delta p = a/
V(ст.2);
Где a – постоянная, зависящая от вида газа. Для одного моля газа
получаем p+a/V(ст.2) = R T / V ; Поправка: при любых давлениях, объем
газа не может стать равным нулю. Уравнение Ван-дер-Ваальса:
(p + a / V (ст.2)) (V - b) = RT, где b – так называемый “запрещенный
объем”
4
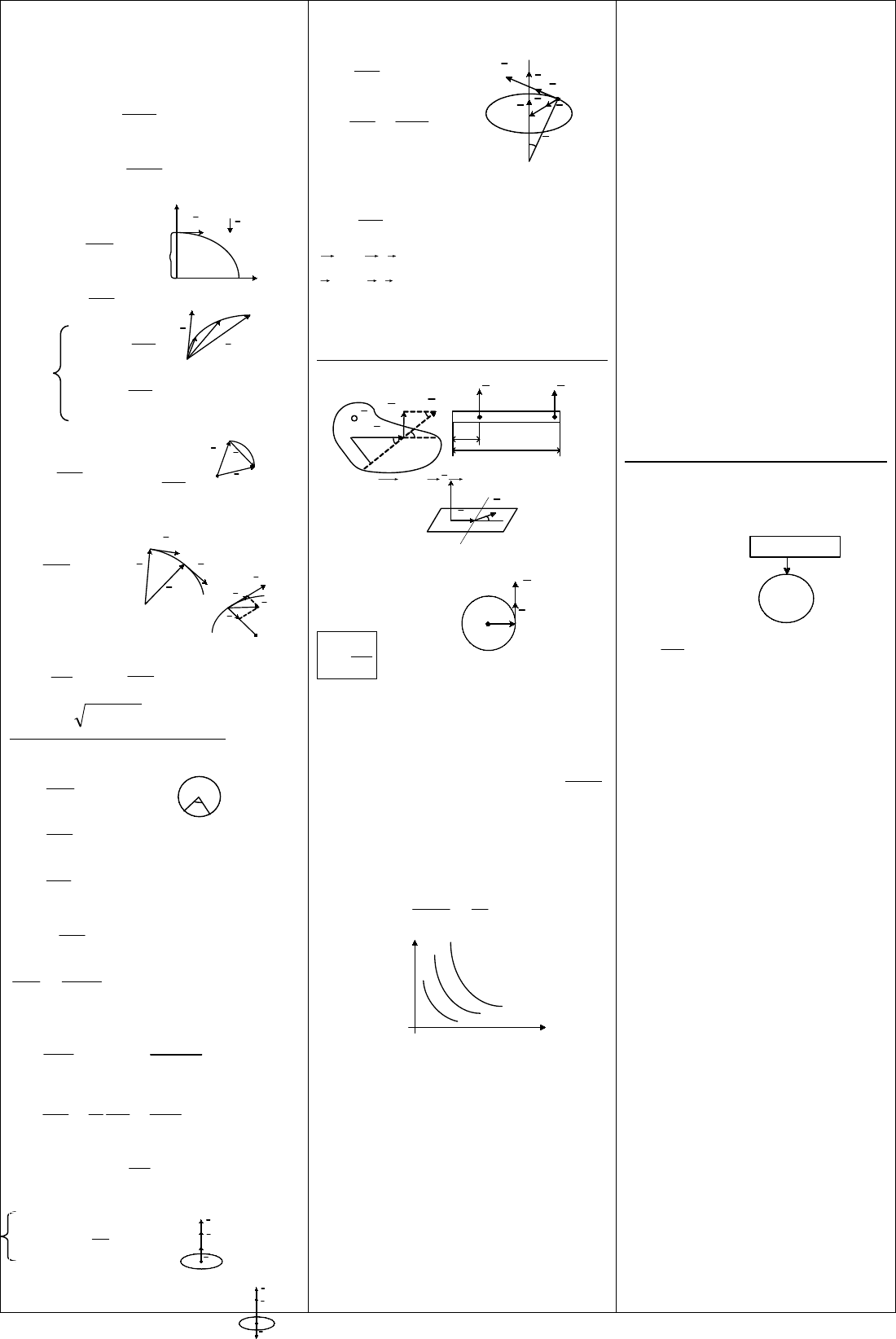
Движение точки по окружности. При равномерном движении мат.точки по
окружности радиус-вектор r точки описывает за время deltaT равные углы
deltaФИ. Отношение deltaФИ / deltaT = ОМЕГАмаленькое, называемое
угловой скоростью, остается постоянным. За время deltaT = Tбольшое, за
которое совершается один оборот, радиус-вектор повернется на угол deltaФИ =
2ПИ. Следовательно ОМЕГАмал. = 2ПИ / T. Учитывая, что частота вращения v
= 1 / T, получим ОМЕГАмал = 2ПИv.
Модуль скорости при таком движении (линейная скорость) равен производной
от длины дуги по времени: скоростьV = ds / dt = s’ ( t ).
(рисунок – окружность, 2 точки, расстояние между ними deltaS, от нуля до точек
проведены вектора r, угол между ними deltaФИ). Так как deltaS = r * deltaФИ, то
между модулями линейной и угловой скорости получается:
v = r dФИ / dt = r ОМЕГАмал. Так как модуль скорости остается неизменным, а
вектор скорости меняется по направлению, то ускорение в этом движении связано
только с изменением направления скорости, т.е.
вектор a нормальное = lim (при delta t 0) вектор delta v нормальное / delta t
= dv нормальное / dt.
(рисунок – точки A и D на окружности, delta s, r, угол АЛЬФА между радиус-
векторами, вектор скорости по касательной к точке A v1 и тоже к точке D v2;
проекция v2 к точке A; теперь расстояние между v1 и v2 = BC = delta v
нормальное; расстояние от точки A до D = delta t)
Из рисунка видно, что треугольник ABC равнобедренный. Если delta t 0, то
угол АЛЬФА между векторами v1 и v2 также стремится к нулю, т.к. сумма углов
в треугольнике равна ПИ, то угол между векторами delta v нормальное и v в
пределе равен ПИ/2. Следовательно вектор нормального ускорения
перпендикулярен вектору скорости. Т.к. вектор скорости всегда направлен по
касательной, то вектор ускорения направлен по радиусу к центру окружности.
Если матерьяльная точка движется по окружности с постоянной по модулю
скоростью, то это движение происходит с ускорением, направленным в каждый
момент времени перпендикулярно вектору скорости.
a нормальное = v (ст.2) / r = v ОМЕГАмал = ОМЕГАмал. (ст.2) r = 4ПИ (ст.2)
r / T (ст.2) = 4ПИ (ст.2) v (ст.2) r
Условие равновесия твердого тела. Всякое движение твердого тела можно
представить как сумму поступательного и вращательного движения. Отсюда
вытекает 2 условия равновесия твердого тела: 1) F1+…+Fn = 0 – тело не движется
поступательно ; 2) M1 +… Mk= 0 – тело не вращается.
Момент инерции тела относительно оси.
Моментом инерции матерьяльной точки относительно оси называется величина
J = m r (ст.2). Где r – расстояние от точки до оси вращения.
Wk = m*v*v / 2. Если тело состоит из нескольких матерьяльных точек, то момент
его инерции будет равен сумме моментов инерций этих точек. Эта формула
справедлива для дискретного распределения масс. В случае непрерывного
распределения масс J = (интеграл) v (ст.2) dm .
Энтропия. Помимо внутренней энергии, которая является только функциональной
составляющей термодинамической системы, в термодинамике используется еще
ряд других функций, описывающих состояние термодинамической системы.
Особое место среди них занимает энтропия. Пусть Q – теплота, полученная
термодинамической системой в изотермическом процессе, а T – температура, при
которой произошла эта передача теплоты. Величина Q/ T называется приведенной
теплотой. Приведенное количество теплоты, сообщаемое термодинамической
системе на бесконечно малом участке процесса будет равно dQ / T. В
термодинамике доказывается, что в любом обратимом процессе сумма
приведенных количеств теплоты, передаваемая системе на бесконечно малых
участках процесса равна нулю. Математически это означает, что dQ/T – есть
полный дифференциал некоторой функции, которая определяется только
состоянием системы и не зависит от того, каким путем перешла система в такое
состояние. Функция, полученный дифференциал которой равен dS= dQ/ T –
называется энтропией. Энтропия определяется только состоянием
термодинамической системы и не зависит от способа перехода системы в это
состояние. S – энтропия. Для обратимых процессов delta S = 0. Для необратимых
delta S > 0 – неравенство Клаудио. Неравенство Клаудио справедливо только для
замкнутой системы. Только в замкнутой системе процессы идут так, что энтропия
возрастает. Если система незамкнута и может обмениваться теплотой с
окружающей средой, ее энтропия может вести себя любым образом ; dQ = T dS ;
При равновестном переходе системы из одного состояния в другое dQ = dU + dA ;
delta S = (интеграл 1 – 2) dQ / T = (интеграл) (dU + dA) / T. Физический смысл
имеет не сама энтропия, а разность энтропий при переходе системы из одного
состояния в другое.
Связь энтропии с вероятностью состояния системы. Более глубокий смысл
энтропии скрывается в статической физике. Энтропия связывается с
термодинамической вероятностью состояния системы. Термодинамическая
вероятность состояния системы – это число способов, которыми может быть
реализовано данное состояние макроскопической системы. Иными словами W –
это число микросостояний, которые реализовывают данные макросостояния.
Больцман методами статистической физики показал, что энтропия S системы и
термодинамическая вероятность связаны соотношением: S= k ln (W) ; где k –
постоянная Больцмана. Термодинамическая вероятность W не имеет с
математической вероятностью ничего общего. Из этого соотношения видно, что
энтропия может рассматриваться как мера вероятности состояния
термодинамической системы, энтропия является мерой неупорядоченной
системы. Чем больше число микросостояний, реализующих данное
макросостояние, тем больше ее энтропия.
5
Постулаты специальной теории относительности. Специальная теория
относительности также как и Ньютоновская механика предполагает, что время
однородно, а пространство однородно и изотопно. В основе специальной теории
относительности лежат 2 постулата, которые являются результатом
эксперементально установленных закономерностей.
1 постулат обобщает принцип механической независимости Галилея на все
физические явления. В любых инерциальных системах отсчета все физические
явления при одних и тех же условиях протекают одинакова.
2 постулат выражает принцип имвариантности скорости света. Скорость света в
вакууме не зависит от скорости движения источника. Она одинакова во всех
направлениях и во всех инерциальных системах отсчета. Скорость света в вакууме
является предельной скоростью в природе.
Эйнштейн пересмотрел классические свойства пространства и времени. Он
предположил, что время в различных инерциальных системах отсчета течет
неодинаково. Пространство и время в теории относительности рассматривается
совместно, а не обособленно, как в Ньютоновской механике. Они образуют единое
4х-мерное пространство и время. Возьмем в таком 4х-мерном пространстве и
времени декартовую систему координат с осями (x, y, z, ct). Положение тела в
таком 4х-мерном пространстве изображается точкой с координатами (x, y, z, ct).
Эта точка называется мировой точкой. Со временем она меняет свое положение,
описывая в 4х-мерном пространстве некоторую линию, называемую мировой
линией. Даже в том случае, если тело остается неподвижным в обычном 3х-
мерном пространстве, его мировая точка перемещается вдоль оси ct.
Выберем 2 инерциальные системы отсчета k (x, y, z, t) и k’ (x’, y’, z’, t’). Будем
считать, что система отсчета k’ движется относительно системы k со скоростью v,
направленной вдоль оси OX. Пусть в начальный момент времени начала этих
систем отсчета совпадают. В этот момент из начала отсчета вдоль оси OX
излучается световой импульс. За время t в системе отсчета k он дойдет до точки ; x
= ct ; x’ = ct’
ГАММА (x - vt) = x’ ; ГАММА (x’ – vt’) = x ;
ГАММА (ct - vt) = ct’ УМНОЖАЕМ НА ГАММА (ct + t) = ct ; ПОЛУЧАЕМ
ГАММА (ст.2) (c (ст.2) – v (ст.2)) = c (ст.2);
ГАММА = 1 / [ (корень) 1 – v(ст.2) / c(ст.2) ] ;
В k : x = (x’ + vt’) / (корень) (1-v(ст.2)/c(ст.2)) ; y = y’ ; z = z’
В k’ : x = (x + vt) / (корень) (1-v(ст.2)/c(ст.2)) ; y = y’ ; z = z’
Используем значение ГАММА из предыдущего выражения:
t = (t’ + x’ v/c (ст.2)) / ((корень) 1 – v(ст.2)/ c (ст.2))
t’ = (t + x v/c (ст.2)) / ((корень) 1 – v(ст.2)/ c (ст.2))
--- ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА!!!!!
Они связывают координаты и время в различных инерциальных системах отсчета.
В приделе при c к бесконечности, преобразования Лоренца переходят в
преобразования Галилея. Различие в течении времени в разных инерциальных
системах отсчета обусловлено существованием предельной скорости
взаимодействий. При малых скоростях движений v0 преобразования Лоренца
переходят в преобразования Галилея.
5 Идеальная тепловая машина Карно.
В ее основе лежит
круговой процесс который называется
циклом Карно
1-2: A
1
=Q
1
>0 – Изотерм. расширение
2-3: Q=0 – Адиабатическое расширение;
3-4: A
2
=Q
2
<0 – Изотермическое сжатие;
4-1: Q=0 Адиабатическое сжатие.
Для замкнутых циклов
работа совершаемая газом в цикле Карно
равна подводимому теплу. Тепловая
машина реализующая этот цикл имеет
максимальный КПД по сравнению с любым другим циклом. =(T
1
-T
2
)/T
1
; Для
повышения КПД тепловых машин Необходимо увеличивать температуру
нагревателя и уменьшать температуру холодильника. КПД любой реальной
тепловой всегда меньше, чем у машины Карно:
1
21
1
21
Q
QQ
T
TT
7
Моментом импульса (моментом количества движения) матерьяльной
точки относительно оси называется векторная величина L = r * P ; где все
величины – векторы ; r – расстояние от оси вращения до этой точки.
Импульс точки: P = mv. Моментом силы M называется величина M=r *F
Моментом импульса твердого тела относительно оси является
L = сумма ri Pi ; |L| = |r | |P| sinАЛЬФА ; Рассмотрим случай, когда
АЛЬФА=ПИ/ 2: L = сумма mi vi ri = w сумма mi vi (ст.2) = J w; L = J w ;
Продефференцируем это выражение по времени: dL / dt = J dw/dt = J
центромасс = M ; dL / dt = M ; Если M= 0, то dL / dt = 0 L = const
Это закон сохранения импульса!!! --- Если на систему тел не действует
момент силы M или равнодействующая всех сил равна нулю, то момент
импульса этой системы остается постоянным. Закон сохранения момента
импульса является фундаментальным законом физики. Он справедлив не
только в классической механике, но и в релитивистской и в квантовой
механике. Закон сохранения момента импульса связан с изотропностью
пространства – пространство обладает одинаковыми свойствами во всех
направлениях.
Вынужденные колебания – это колебания, возникающие в колебательной
системе под влиянием переменного внешнего воздействия.
Колебания называют переодическими, если значения всех физических
величин, характеризующих колебательную систему повторяется через
равные промежутки времени. Наименьший промежуток времени,
удовлетворяющий этому условию называется периодом колебания T.
Вынужденные колебания осциллятора под действием синусоидальной
силы. ; ma = F ; m d2 x / dt (ст.2) = F ; Fупр = - kx ; Fтр = - b dx / dt ; F = F0
sinΩt ; (d2 x / dt (ст.2)) + (2 БЕТА dx / dt) + w 0 (ст.2) = (F0 / m) sinΩt ;
Это дифференциальное уравнение описывает вынужденные колебания. В
общем случае общее решение этого неоднородного дифференциального
уравнения имеет вид: X(t) = X1(t) + X2(t) ; X1(t) является общим
решением однородного диф. уравнения, описывающего свободный
гармонический затухающий осциллятор. Видно, что после начала
действия вынуждающей силы возникает сложный колебательный процесс,
состоящий из суммы 2х колебаний – затухающего колебания X1(t) с
частотой wt и незатухающего колебания с частотой Ωt. X1(t) за достаточно
небольшой промежуток времени затухает и остается только одно
колебание с частотой вынужденной силы Ω0. Это время, в течении
которого X1(t) затухает, называется временем установки вынужденных
колебаний. Чем больше добротность осциллятора, тем больше время
установления ТАУ~10 Q/w0 (это время, в течении которого амплитуда
затухающего колебания уменьшится в 100 раз).
В общем случае установившееся вынужденное колебание имеет вид:
X = A sin (Ωt + ФИ) ; непосредственно подставляя это выражение в
дифференциальное уравнение вынужденного колебания можно получить:
A = F0 / m (корень (w 0 (ст.2) – Ω(ст.2) + ФИ БЕТА (ст.2) Ω (ст.2)) ;
tgФИ = - 2 БЕТА Ω / (w 0 (ст.2) – Ω (ст.2))
1. при Ω=0 ; A = F0 / m w 0 (ст.2) = F0 / k – статическое смещение.
2. при ΩБЕСКОНЕЧНОСТЬ ; A0 ;
Максимум амплитуды вынужденных колебаний достигается при частоте
Ω = (корень w 0 (ст.2) – БЕТА (ст.2)) ;
При частоте w = (корень w 0 (ст.2) – БЕТА (ст.2)) амплитуда достигает
максимума: Amax = F0 / 2 m БЕТА Ω
Явление резкого возрастания амплитуды вынужденных колебаний при
совпадении частоты вынужденной силы с соответственной частотой
колебаний системы называется резонансом. Амплитуда колебаний при
резонансе зависит от затухания, чем оно больше, тем меньше амплитуда.
При нулевом затуханиии амплитуда колебаний при резонансе достигает
бесконечно большой величины.
V
0
P
1
2
3
4
Q
1
Q
2
6При движении материальная точка описывает некоторую линию, т. о. положению точки и
соответствует радиус-вектор, который и является функцией времени. Уравнение движения
– функция, дающая возможность определить положение точки в любой момент времени.
)(
)(
tfy
tfx
y
x
r = x
(t)
i + y
(t)
j + z
(t)
k;
Уравнения движения:
1)
a
=const
2
2
0
0
ta
txx
x
x
2
2
00
ta
tyy
y
н
2) x(t)=Acos(ωt + φ);
2
2
0
at
tS
Траектория (путь), Перемещение(Вектор)
t
r
мгн
t
x
x
t
y
y
мгн
– всегда касательная к траектории.
t
S
ср
dt
dS
мгн
Ускорение – характеризует быстроту изменения скорости.
t
a
Полное ускорение разделяют на 2-е составляющие:
1)Тангенсальную (касательную) – характеризует изменение скорости по величине.
2)Нормальную – характеризует изменение скорости по направлению
R
a
н
2
dt
d
a
22
нполное
aaa
§1.3 Кинематические характеристики вращательного движения.
Вращательное - движение, когда все точки тела движутся по концентрическим
окружностям, центры которых лежат на одной прямой, которая называется осью вращения.
ω - угловая скорость, характеризующая быстроту углового перемещен
t
– средняя скорость
dt
d
– мгновенная скорость
2
2
T
- равномерное угловое вращение;
[ω] = Рад/сек.
R
L
RL
t
R
t
R
R
– линейная скорость вращения
- угловое ускорение, характеризует быстроту изменения угловой скорости.
t
;
dt
d
Связь между характеристикой поступательного и вращательного движения
Radt
d
Rdt
d 11
Ra
R
R
a
н
2
2
Если
-const, то угловой путь и угловая скорость определяется
2
0
2
t
t
t
0
‘+’-равноускоренное движение
Векторное представление угловых характеристик.
a) Ускоренное вращение
8
Если точка движется криволинейно, то в каждый момент времени
ее движение может быть представлено как движение по окружности с радиусом R.
Ее движение может быть описано с помощью радиус-вектора, который проведен
из (0;0) в точку, где находится тело:
dt
d
2
2
dt
d
dt
d
RV
Ra
R
R
V
a
n
2
2
R=rsin, V=rsin,
],[ rV
],[ ra
Основное уравнение динамики вращательного движения. Wk = 1/2 J * w(ст.2) ;
dWk = 1/2 J 2w dw = Jwdw ; dWk = dA ; M dФИ = Jwdw;
M dФИ/dt = Jw dw/dt ; w = dФИ/dt ; E = dw/dt ; M w = J w E ; M = J E (M,E -
вектора). Основное уравнение динамики вращательного движения. Это аналог 2го
закона Ньютона для вращательного движения. (F-M, m-J, a-E).
Опыт показывает, что одна и та же сила оказывает разное
вращательное действие.
],[ FRM
M=FRsinα
F
τ
=Fsinα
M=F
τ
R
Действие касательной силы на материальную точку может
привести к движению с тангенсальным ускорением:
F
=ma
a=R
F
= mR
F
R=mR
2
M=J
M=F
R
J=mR
2
- момент инерции
J
M
– угловое ускорение
Термодинамика является вторым подходом к изучению тепловых
явлений. В этом случае в явном виде не учитываются внутреннее строение
вещества. Термодинамика оперирует макроскопическими величинами такими как:
P, V, T, , n. В основе термодинамики лежат эмпирические законы, которые
называются началами термодинамики.
1)Термодинамической системой называется любая
макроскопическая система тел или одно тело, между которыми происходит обмен
энергии.
2)Равновесным состоянием термодинамической системы
называют такое состояние, когда все макроскопические характеристики не
изменяются с течением времени и их значение во всех частях системы одинаково.
3)Температура в термодинамике имеет смысл только для
равновесных состояний. Температура характеризует интенсивность теплового
движения.
4)Термодинамический процесс. При изменении внешних
условий параметры системы будут изменяться т.е. будет изменяться состояние
системы. Это изменение состояния и называется термодинамическим процессом.
Термодинамический процесс называется равновесным, если система проходит
через непрерывный ряд бесконечно близких равновесных состояний.
Диаграмма состояний.
Состояние системы определяется одной точкой.
Пример: Изотермический процесс: T=const
V
C
V
RT
P
9
Постулаты специальной теории относительности. Специальная теория
относительности также как и Ньютоновская механика предполагает, что
время однородно, а пространство однородно и изотопно. В основе
специальной теории относительности лежат 2 постулата, которые
являются результатом эксперементально установленных закономерностей.
1 постулат обобщает принцип механической независимости Галилея на
все физические явления. В любых инерциальных системах отсчета все
физические явления при одних и тех же условиях протекают одинакова.
2 постулат выражает принцип имвариантности скорости света. Скорость
света в вакууме не зависит от скорости движения источника. Она
одинакова во всех направлениях и во всех инерциальных системах
отсчета. Скорость света в вакууме является предельной скоростью в
природе.
Эйнштейн пересмотрел классические свойства пространства и времени.
Он предположил, что время в различных инерциальных системах отсчета
течет неодинаково. Пространство и время в теории относительности
рассматривается совместно, а не обособленно, как в Ньютоновской
механике. Они образуют единое 4х-мерное пространство и время.
Возьмем в таком 4х-мерном пространстве и времени декартовую систему
координат с осями (x, y, z, ct). Положение тела в таком 4х-мерном
пространстве изображается точкой с координатами (x, y, z, ct). Эта точка
называется мировой точкой. Со временем она меняет свое положение,
описывая в 4х-мерном пространстве некоторую линию, называемую
мировой линией. Даже в том случае, если тело остается неподвижным в
обычном 3х-мерном пространстве, его мировая точка перемещается вдоль
оси ct.
Выберем 2 инерциальные системы отсчета k (x, y, z, t) и k’ (x’, y’, z’, t’).
Будем считать, что система отсчета k’ движется относительно системы k
со скоростью v, направленной вдоль оси OX. Пусть в начальный момент
времени начала этих систем отсчета совпадают. В этот момент из начала
отсчета вдоль оси OX излучается световой импульс. За время t в системе
отсчета k он дойдет до точки ; x = ct ; x’ = ct’
ГАММА (x - vt) = x’ ; ГАММА (x’ – vt’) = x ;
ГАММА (ct - vt) = ct’ УМНОЖАЕМ НА ГАММА (ct + t) = ct ;
ПОЛУЧАЕМ ГАММА (ст.2) (c (ст.2) – v (ст.2)) = c (ст.2);
ГАММА = 1 / [ (корень) 1 – v(ст.2) / c(ст.2) ] ;
В k : x = (x’ + vt’) / (корень) (1-v(ст.2)/c(ст.2)) ; y = y’ ; z = z’
В k’ : x = (x + vt) / (корень) (1-v(ст.2)/c(ст.2)) ; y = y’ ; z = z’
Используем значение ГАММА из предыдущего выражения:
t = (t’ + x’ v/c (ст.2)) / ((корень) 1 – v(ст.2)/ c (ст.2))
t’ = (t + x v/c (ст.2)) / ((корень) 1 – v(ст.2)/ c (ст.2))
--- ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА!!!!!
Они связывают координаты и время в различных инерциальных системах
отсчета. В приделе при c к бесконечности, преобразования Лоренца
переходят в преобразования Галилея. Различие в течении времени в
разных инерциальных системах отсчета обусловлено существованием
предельной скорости взаимодействий. При малых скоростях движений
v0 преобразования Лоренца переходят в преобразования Галилея.
Невозможен процесс результатом которого является
превращение всей теплоты полученной от нагревателя в эквивалентную
механическую работу. Другими словами этот закон эквивалентен
утверждению о невозможности вечного двигателя 2-го рода.
Схема вечного двигателя 2 рода:
%100*
1
Q
A
Следствие:
1)2-й закон Термодинамики запрещает использовать
энергию системы находящейся в термодинамическом равновесии.
2)Для преобразования тепловой энергии должны быть две
системы находящееся при разных температурах. Невозможно
преобразование всей энергии теплового, хаотического движения в
упорядоченную энергию мех. движения. Возможно лишь частичное
преобразование внутренней энергии и только при наличии двух систем не
находящихся в тепловом равновесии. Другая часть энергии передается
холодильнику. Преобразование внутренней энергии теплового
хаотического движения в мех. работу в термодинамике характеризуется
двумя величинами, которые наряду с внутренней энергией являются
функциями состояний системы. Это: F-свобод. энергия. S–энтропия. Все 3
функции состояния связаны соотношением
U=F+TS
Свободная энергия та часть внутренней энергии, которая
может быть преобразована в механическую энергию.
(TS) - связанная энергия – это та часть, которая не может
быть преобразована в механическую энергию.
R
V
a
a
n
0
r
R
2
R
1
0
F
1
F
2
*
F
F
L
0
R
M
F
R
M
a
R
F
P
V
0
T
1
T
2
T
3
T
1
<T
2
<T
3
нагреватель T
1
рабочее
тело
Q
1
=> A=Q
1
y
x
V
0
g
h
(
t
r, )
r
r
(t)
r
(t+
t)
r
S
0
V
1
V
2
r
1
r
2
a
n
a
V
a
L
R
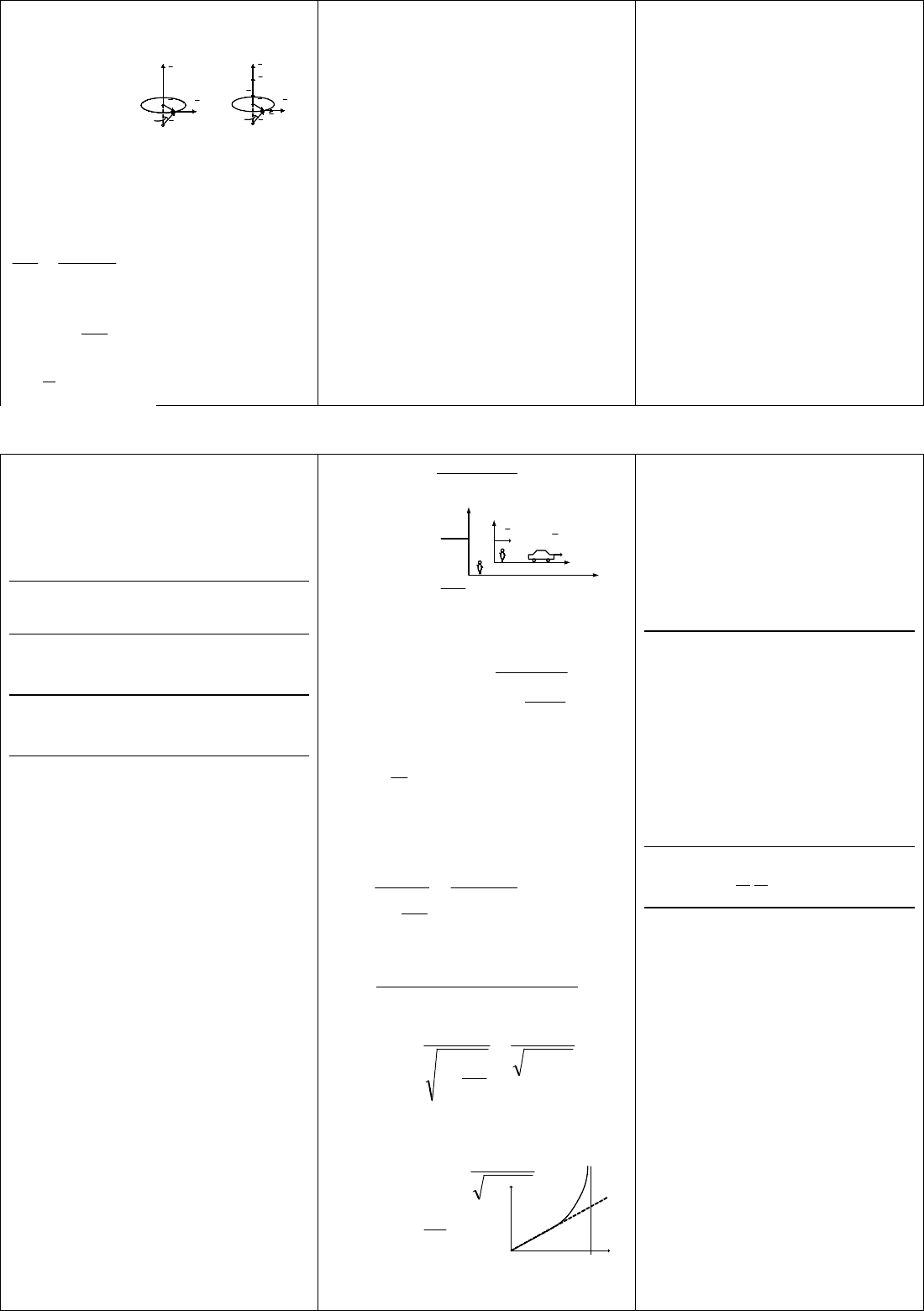
>0
>0
t
12
б) Замедленное вращение
0
0
t
12
υ=[ωr];
υ=[ωR]
υ=ωrsinθ
rRa
Постоянное тепловое хаотическое движение приводит к непрерывному перемещению
молекул. При этом если в газе возникают какая либо неоднородность то со временем все
неоднородности выравниваются. Эти процессы выравнивания не являются хаотическими, а
характеризуются определенной направленностью. Это связано с перемещением
характеристик газа от областей с избытком к областям с недостатком. Существует 3 типа
неоднородностей:
1)Неоднородность плотности (концентрации);
2)Неоднородность температуры (энергии);
3)Неоднородность импульса (перемещения) отдельных слоев движения газа;
Диффузия – процесс самопроизвольного выравнивания концентрации.
Рассмотрим перенос вещества вдоль направления оси X. Пусть
1
>
2
, Изменение
плотности вдоль X характеризуется градиентом плотности:
0
12
12
xxx
Если плотность распределяется неравномерно перенос вещества в следствии диффузии
определяется уравнением Фика:
Sdt
dx
d
Ddm
D – коэффициент диффузии
3
1
D
10
Физический маятник – это твердое тело, способное совершать колебания под
действием своей силы тяжести вокруг оси, не проходящей через центр тяжести
тела. Эта ось называется осью качания.
M = - J E ; M = m g d * sinφ (где d – расстояние от центромасс до места крепления
физического маятника) ; J E = - mgd sinφ ; E = d2 φ / dt (ст.2) ;
J * (d2 φ / dt (ст.2)) + mgd sinφ = 0 ; d2 φ / dt (ст.2) + (mgd / J) sinφ = 0 ;
Это дифференциальное уравнение, описывающее колебания физического
маятника. При малых углах уклонения можно считать, что sinφ = φ радиан ;
(d2 φ / dt (ст.2)) + mgdφ / J = 0 ; Это дифференциальное уравнение описывает
гармонические колебания, частота которых равна:
d2 S / dt (ст.2) + w0 (ст.2) S = 0 ; w0 (ст.2) = mgd / J ; w0 = корень (mgd / J) ;
T = 2ПИ / w0 = 2ПИ (корень J / mgd).
Если твердое тело представляет собой матерьяльную точку, подвешенную на
невесомой, нерастяжимой нити и способную совершать колебания, то маятник
будет математическом. J = md (ст.2) ; T = 2ПИ (корень md(ст.2) / mgd) = 2ПИ
(корень d / g); T = 2ПИ (корень d / g) – период колебания математического
маятника.
Малые колебания физического и математического маятника представляет из себя
пример изохронных колебаний, т.е. колебаний, частота которых не зависит от
амплитуды. В общем случае период колебаний физического маятника зависит от
амплитуды: T = 2ПИ (корень J / mgd) * [1 + 1/2 (ст.2) sin (ст.2) (φ/2) + (1/2 * 3/4)
(ст.2) sin (ст.2) (φ/2) + …]. А та формула дает погрешность не более 1,5% для
углов отклонения, не превышающих 15 градусов.
Пружинный маятник. Рассмотрим колебания груза на пружине:
Fупр = - kx (закон Гука); ma = Fупр ; m * (d2 x / dt (ст.2)) = - kx ;
(d2 x / dt (ст.1)) + kx / m = 0 – это дифференциальное уравнение, описывающее
колебания груза на пружине, жесткость которого равна k.
Частота этих колебаний: w 0 = (корень) k / m ;
Период: T=2ПИ (корень m / k)
11
Сложение скоростей.
Преобразования Лоренца позволяют получить:
dt
dx
U
td
dx
U
x
x
'
2
1
c
VU
VU
U
x
x
x
VUU
c
V
ипр
xx
1
Пример: Определить скорость фотона относительно Земли, если его испускает
фонарик, находящийся на космическом корабле движущемся со скоростью V в
направлении движения.
Относительно S`: U`
x
=c
Относительно наблюдателя в системе S:
c
Vc
Vcc
c
cV
Vc
U
x
)(
1
2
Отсюда видно, что релятивистский способ сложения скоростей
соответствует 2-му постулату специальной теории относительности: Скорость
света во всех инерциальных системах отсчета одинакова.
§7.2 Импульс и энергия в релятивистской динамике.
Время, масса и длина – относительные величины в механике.
Значит, масса зависит от того, в какой системе отсчета она была измерена.
2
0
2
2
0
1
1
m
c
V
m
m
При больших скоростях масса возрастает.
m
0
– масса покоя, т.е. масса измеренная относительно той
системы отсчета, в которой тело покоится =>
cV
dt
pd
F
Vm
mVp
2
0
1
Полную энергию можно выразить через массу покоя:
12
Моментом импульса (моментом количества движения) матерьяльной
точки относительно оси называется векторная величина L = r * P ; где все
величины – векторы ; r – расстояние от оси вращения до этой точки.
Импульс точки: P = mv. Моментом силы M называется величина M=r *F
Моментом импульса твердого тела относительно оси является
L = сумма ri Pi ; |L| = |r | |P| sinАЛЬФА ; Рассмотрим случай, когда
АЛЬФА=ПИ/ 2: L = сумма mi vi ri = w сумма mi vi (ст.2) = J w; L = J w ;
Продефференцируем это выражение по времени: dL / dt = J dw/dt = J
центромасс = M ; dL / dt = M ; Если M= 0, то dL / dt = 0 L = const
Это закон сохранения импульса!!! --- Если на систему тел не действует
момент силы M или равнодействующая всех сил равна нулю, то момент
импульса этой системы остается постоянным. Закон сохранения момента
импульса является фундаментальным законом физики. Он справедлив не
только в классической механике, но и в релитивистской и в квантовой
механике. Закон сохранения момента импульса связан с изотропностью
пространства – пространство обладает одинаковыми свойствами во всех
направлениях.
Уравнение состояния идеального газа. Параметры состояния связаны
друг с другом. Уравнение состояния устанавливает связь между
параметрами состояния. В простейшем случае состояние
термодинамической системы описывается тремя параметрами – P, V, T.
F (P, V, T) = 0 ; Идеальный газ – это модель, которая во многих случаях с
достаточно хорошей точностью описывает поведение газа. Идеальный газ
– это газ, молекулы которого имеют пренибрежительно малый объем и не
взаимодействуют на расстоянии. Молекулы идеального газа
взаимодействуют друг с другом только в момент соударения. Причем
соударение считается абсолютно упругим. Эти предположения
(отсутствие взаимодействия, абсолютно упругие соударения) позволяют
утверждать, что внутренняя энергия идеального газа определяется суммой
кинетических энергий отдельных частиц, причем эта кинетическая
энергия не переходит ни в какие другие виды энергии. Опытным путем
было установлено, что параметры состояния газа удовлетворяют условию
PV / T = const ; зависящему от количества вещества ; PV / T = МЮ R ; (R –
универсальная газовая постоянная = 8,31 дж/моль к) ; PV = МЮ RT –
уравнение Менделеева-Клайперона. МЮ = m / μ ; 1 моль любого газа
при нормальных условиях занимает ; R = k Na ; PV = МЮ Na kT ; МЮ Na
= N ; PV = NkT ; P = N k T/ V ; N0 = N/ V – число молей в единице объема.
P = n0 k T – другая форма записи этого уравнения.
Дано: m
1
=3 кг; m
2
=3 кг; M
1
=4010
-3
кг/моль; M
2
=2810
-3
кг/моль;c
p
-?
Решение: Q=c
v
mT; m=m
1
+m
2
; Q=Q
1
+Q
2
; Q
1
=c
v1
m
1
T;
Q
2
=c
v2
m
2
T; c
v
mT=c
v1
m
1
T+c
v2
m
2
T; c
v
=(c
v1
m
1
+c
v2
m
2
)/(m
1
+m
2
);
c
p
=(c
p1
m
1
+c
p2
m
2
)/(m
1
+m
2
); i
1
=6; i
2
=5; c
p1
=((i
1
+2)/2)(R/M
1
);.
c
p2
=((i
2
+2)/2)(R/M
2
); c
p
=(R/2)(((i
1
+2)m
1
)/M
1
+((i
2
+2)m
2
)/M
2
)
1/(m
1
+m
2
);
S
y
x
S'
y'
x'
U'
x
V
p
=V/c
1
R
r
V
R
r
V
a
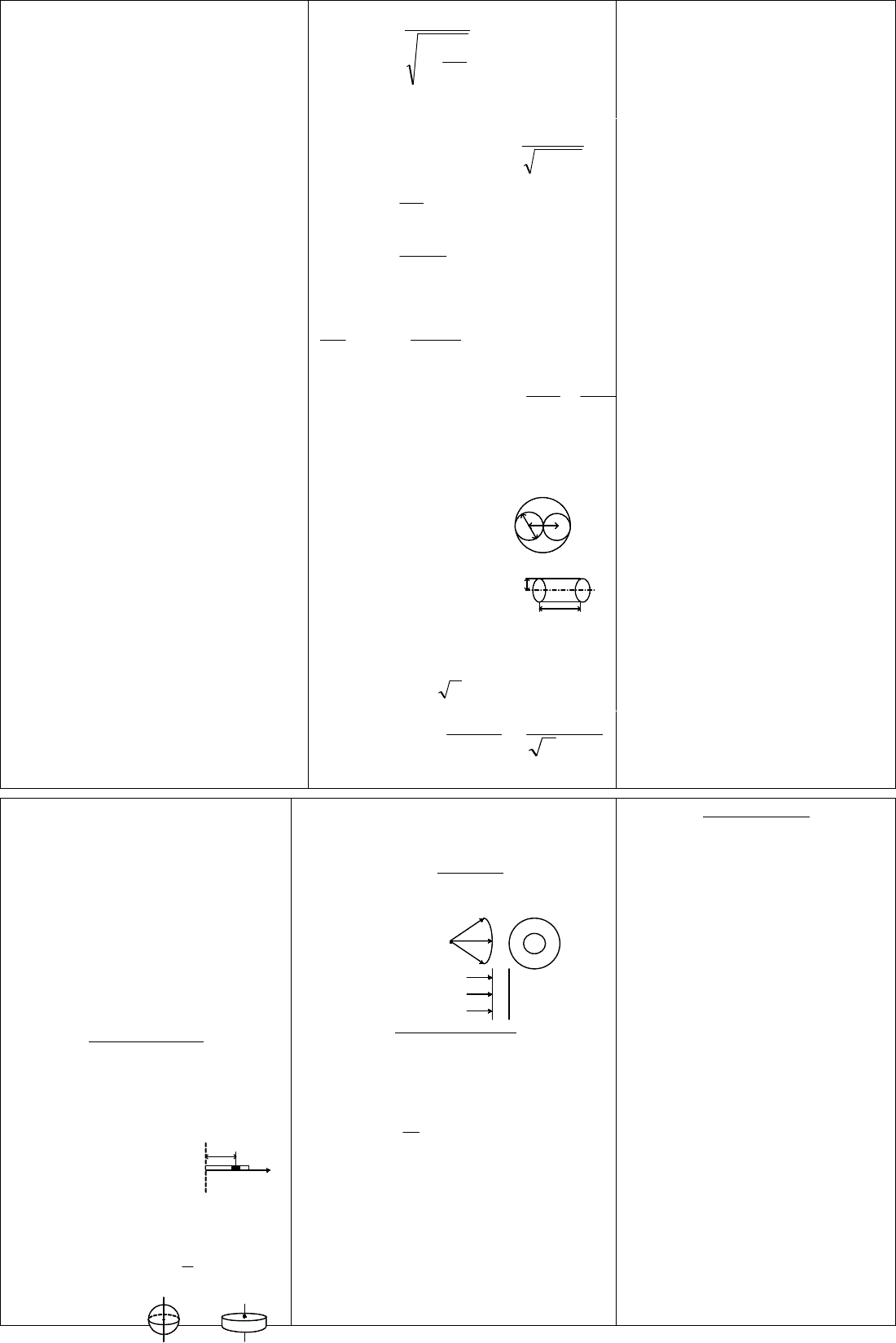
2
2
2
0
2
1
c
V
cm
mcE
2
00
cmE
- энергия покоя.
22
)
2
1(
2
)()(
)1
1
1
(
)1(
)1
1
1
(
1
2
0
0
2
2
0
2
0
2
22
0
22
2
2
0
0
2
0
2
2
0
2
0
2
2
0
2
0
2
0
Vm
m
p
KcmKЕсли
cm
K
K
m
p
cmpcE
p
cmK
m
m
cmK
cmcm
cm
mmcEEK
Длина свободного пробега – расстояние между двумя
последовательными соударениями молекул в газе.<λ> Достаточно большой круг
явлений может быть описан с помощью простейшей механической модели,
согласно которой молекулы представлены в виде шариков, которые испытывают
упругие соударения между собой и стенками сосуда. Минимальное расстояние, на
которое могут сблизиться молекулы называется эффективным диаметром и
принимается за диаметр шариков.
Круг площадью d
2
- называется эффективным сечением. Найдем
среднее число соударений которые испытывает молекулы при хаотическом
движении <Z>; Пусть все молекулы покоятся и движется только одна. За 1 сек.
молекула пройдет расстояние равное <>
При этом она столкнется со всеми молекулами которые находятся
в пределах эффективного сечения т.е. находится в цилиндре высотой <> и
площадью сечения равной d
2
если n – концентрация молекул, то
<Z>=nV=nd
2
<>
Учет движения всех частиц приведет к:
2
2 dnZ
Средний путь за 1 сек. т.е. длина свободного пробега:
Pd
kT
nd
Z
22
22
1
13
Релятивистский импульс. Уравнение движения релятивистских частиц
Законы сохранения должны быть соблюдены во всех инерциальных системах
отсчета, т.е. должны быть имвариантны по отношению к преобразованиям
Лоренца. Если определить импульс тела как P = mv (как в Нбюоновской
механике), то можно показать (рассмотрим например неуправляемые
соударения частиц), что в релятивистском случае при определении P, закон
сохранения не будет имвариантен по отношению к преобразованиям
Лоренца. Можно показать, что закон сохранения импульса будет
имвариантен по отношению к преобразованиям Лоренца, если определить
импульс как P = m0 v / (корень 1 – v (ст.2) / c (ст.2)).
Величина m0 – масса покоя частиц. Если через m обозначить величину
m = m0 / корень…, то импульс частицы будет записан также как в
Ньютоновской механике P = mv , где m – релятивистская масса частиц.
Видно, что релятивистская масса частиц изменяется при изменениии
скорости ее движения. Из 2х возможных (в Ньют. мех.) формулировок 2го
закона Ньютона (F=ma ; dP / dt = F) будет справедлива 2ая.
Второй закон будет иметь вид: (d/dt) * (m0 v / корень…) = F – основной
закон в рел. механике. В релятивистском случае масса утрачивает
пропорцианальность между силой и ускорением. В релятивистской механике
сила и ускорение (в отличие от Ньютоновской механики) не являются
имвариантными по отношению к преобразованиям Лоренца, т.е. изменяются
при переходе от одной инерциальной системы отсчета к другой. Кроме этого
сила F и ускорение a оказываются неколлинеарными
Вычисление момента инерции.
i
ii
rmJ
2
Теорема Штейнера: Момент инерции тонкого стержня
dJ=dmx
2
=m/ L – линейная плотность
dm=dx
dJ= x
2
dx
2
0
2
0
3
1
mldxxdJJ
ll
Моменты инерции тел:
14
Упругими или механическими волнами называют процесс
распространения в среде. Акустическими или звуковыми называют колебания с
частотой - =(16-20000)Гц.
<16 – инфразвук.
>20000 – ультразвук.
Распространение волн не сопровождается переносом вещества. При
этом частицы совершают гармонические колебания относительно центра равновесия.
Если колебания происходят направлению скорости волны, то они – поперечные, если
|| - то продольные. Фронт волны – геометрическое место точек, до которого доходят
колебания источника.
§10.2 Уравнение бегущей волны.
Бегущие волны – волны переносящие энергию.
Уравнение бегущей волны – функция, показывающая положение
частиц от времени.
S(x,t)
S(t)=Acos(t)
V
x
t
В некотором направлении X, при скорости волны V, колебания точки
на расстоянии x будут запаздывать на Δt. Поэтому смещение будет равно:
S(x,t)=Acos(ω(t–Δt))=Acos(ω(t–x/V))
Расстояние, которое проходит волна за один период, называют
длинной волны.
15
Уравнение Ван-дер-Ваальса.
Процесс распространения колебаний в сплошной среде называется
волновым процессом или волной. Стоячая волна энергии не переносит.
Стоячие волны образуюся в результате интерференции (наложения) 2х
одинаковых, противоположных по направлению волн. Энергия,
переносимая волной количественно характеризуется вектором плотности
потока энергии, вектором Умова.
y = A sin (wt + φ0)
Колебания в точку, расположенную на расстоянии X от начала координат
приходит с запозданием на время x/v и среднее колебание в точке, с
координатами X будет описываться выражением:
y (x, t) = A sin [w (t – x/v) + φ0] ; w (t – x/v) = wt – wx/v ; w = 2ПИ/ T ;
λ = vT T = λ / v ; w = 2ПИ v/ λ ;
X = 2ПИ / λ – ВОЛНОВОЕ ЧИСЛО (волновой вектор) – вектор,
направление которого совпадает с направлением движения волны.
y (x, t)= Asin (wt – kx + φ0) – уравнение плоской синусоидальной бегущей
волны, распространяющейся в положении направления оси X. Учитывая
формулу Эйлера, эту плоскую волну можно записать в виде
y (x, t) = A e (ст. i (wt – kx + φ)) ; sinx(t) = A sin (wt – kx + φ0).
Фазовая скорость волны – это скорость распространения точки с
постоянной фазой – Ф = const ; v = dx / dt ; Дифференцируем Ф и
получаем:
dФ = d (wt – kx – φ0) = wdt – kdx dx / dt = w/k – фазовая скорость
волны!
Стоячая волна энергии не переносит. Стоячие волны образуюся в
результате интерференции (наложения) 2х одинаковых, противоположных
по направлению волн. Энергия, переносимая волной количественно
характеризуется вектором плотности потока энергии, вектором Умова.
y = A sin (wt + φ0)
Колебания в точку, расположенную на расстоянии X от начала координат
приходит с запозданием на время x/v и среднее колебание в точке, с
координатами X будет описываться выражением:
y (x, t) = A sin [w (t – x/v) + φ0] ; w (t – x/v) = wt – wx/v ; w = 2ПИ/ T ;
λ = vT T = λ / v ; w = 2ПИ v/ λ ;
X = 2ПИ / λ – ВОЛНОВОЕ ЧИСЛО (волновой вектор) – вектор,
направление которого совпадает с направлением движения волны.
y (x, t)= Asin (wt – kx + φ0) – уравнение плоской синусоидальной бегущей
d
d
d
O
O'
0
x
dx
L
S
*
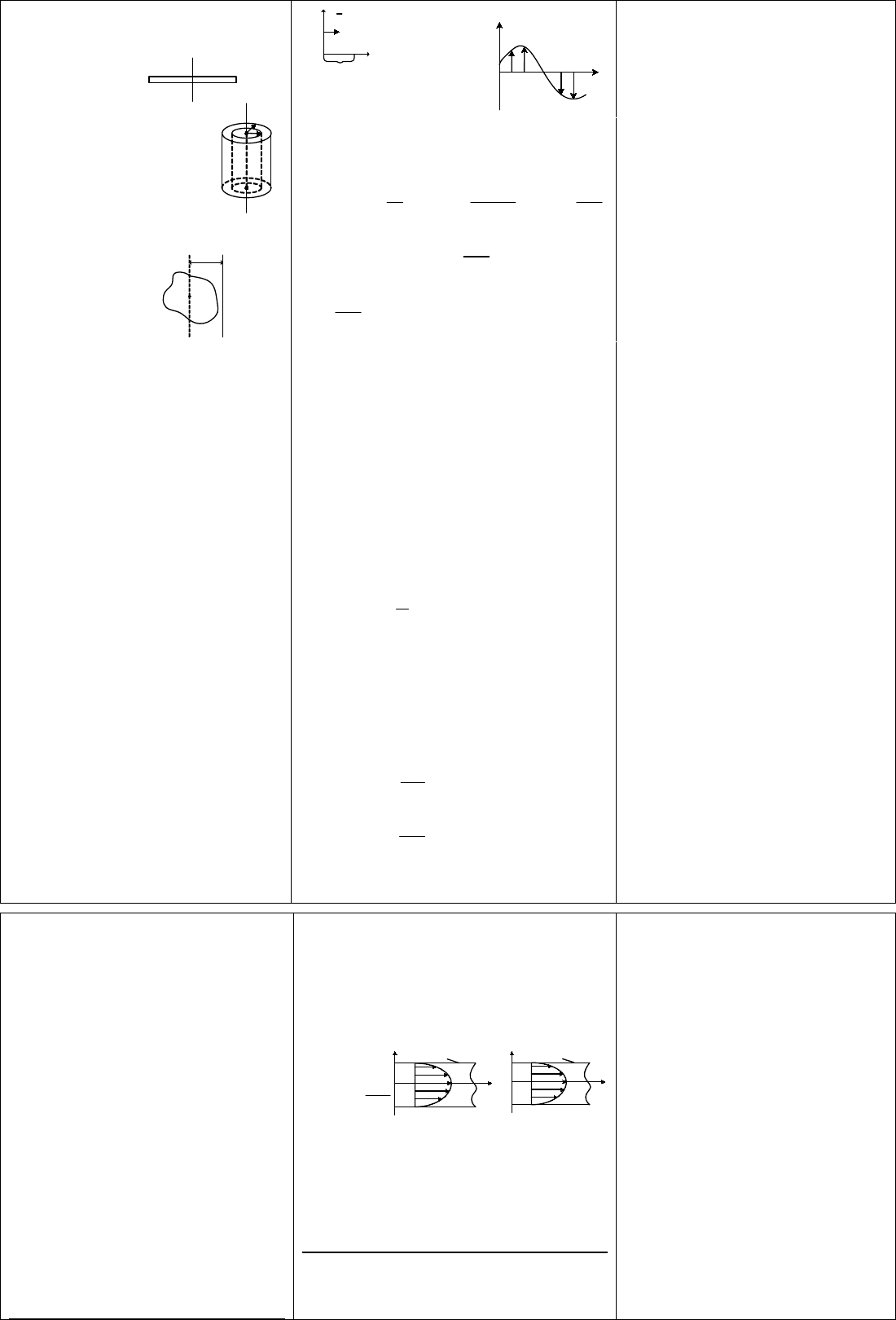
1) Материальная точка J=mR
2
2) Обруч J=mR
2
3) Диск (цилиндр) J=1/2mR
2
4) Шар J=2/5mR
2
5) Тонкий стержень J=1/12mL
2
6) Полый цилиндр J=1/2(R
1
2
+R
2
2
)
Если известен момент инерции относительно оси, проходящей через центр
инерции J
0
, то момент инерции J относительно другой оси, параллельной
первой, можно вычислить по формуле J=J
0
+ md
2
числоволновоеk
xtAtxS
xt
x
t
V
x
t
V
VT
2
)
2
cos(),(
22
)(
Реальные газы. При движении молекулы вдали от стенок сосуда, в котором заключен
газ, на нее действуют силы притяжения соседних молекул, но равнодействующая всех
этих сил в среднем равна нулю, т.к. молекулу со всех сторон окружает в среднем
одинаковое число соседей. При приближении некоторой молекулы к стенке сосуда все
остальные молекулы газа оказываются по одну сторону от нее и равнодействующая
всех сил притяжения оказывается направленной от стенки сосуда внутрь газа. Это
приводит к тому, что уменьшается импульс, передаваемый молекулой стенке сосуда. В
результате давление газа на стенки сосуда уменьшается по сравнению с тем, каким оно
было бы в отсутствие сил притяжения между молекулами: p = p идеального + delta p.
Вместо уравнения идеального газа получаем p + delta p = nkT ; delta p = a/V(ст.2);
Где a – постоянная, зависящая от вида газа. Для одного моля газа получаем p+a/V(ст.2)
= R T / V ; Поправка: при любых давлениях, объем газа не может стать равным нулю.
Уравнение Ван-дер-Ваальса:
(p + a / V (ст.2)) (V - b) = RT, где b – так называемый “запрещенный объем”
Учет межмолекулярных взаимодействий был произведен впервые
голландским физиком Ван-дер-Ваальсом. При этом он исходил из простой модели,
которая была основана на следующих положениях:
1)Молекулы газов представляют собой шары с эффективным
диаметром.
2)Между молекулами существуют только силы притяжения
3)Силы отталкивания учтены введением эффективного диаметра.
Учет собственного объема молекулы
3
6
1
dV
приводит к тому, что «Свободный» молярный
объем в сосуде уменьшается по сравнению с идеальным газом на величину b,
bVV
*
, где b – постоянная Ван-дер-Ваальса.
vrNb
A
Наличие сил притяжения между молекулами реального газа приводит
к тому, что давление становится меньше на некоторую величину p*.
Таким образом
*
ppp
ид
Величина P* согласно теории Ван-дер-Ваальса обратно
пропорциональна квадрату объема:
2
*
V
a
p
, т.о. уравнение состояния имеет вид:
RTbV
V
a
p ))((
2
Для разреженных газов размерами атомов можно пренебречь.
Уравнение Ван-дер-Ваальса переходит в обычное уравнение Менделеева-Клапейрона.
волны, распространяющейся в положении направления оси X. Учитывая
формулу Эйлера, эту плоскую волну можно записать в виде
y (x, t) = A e (ст. i (wt – kx + φ)) ; sinx(t) = A sin (wt – kx + φ0).
Фазовая скорость волны – это скорость распространения точки с
постоянной фазой – Ф = const ; v = dx / dt ; Дифференцируем Ф и
получаем:
dФ = d (wt – kx – φ0) = wdt – kdx dx / dt = w/k – фазовая скорость
волны!
16
Постулаты специальной теории относительности. Специальная теория
относительности также как и Ньютоновская механика предполагает, что время
однородно, а пространство однородно и изотопно. В основе специальной
теории относительности лежат 2 постулата, которые являются результатом
эксперементально установленных закономерностей.
1 постулат обобщает принцип механической независимости Галилея на все
физические явления. В любых инерциальных системах отсчета все физические
явления при одних и тех же условиях протекают одинакова.
2 постулат выражает принцип имвариантности скорости света. Скорость
света в вакууме не зависит от скорости движения источника. Она одинакова
во всех направлениях и во всех инерциальных системах отсчета. Скорость
света в вакууме является предельной скоростью в природе.
Эйнштейн пересмотрел классические свойства пространства и времени. Он
предположил, что время в различных инерциальных системах отсчета течет
неодинаково. Пространство и время в теории относительности
рассматривается совместно, а не обособленно, как в Ньютоновской механике.
Они образуют единое 4х-мерное пространство и время. Возьмем в таком 4х-
мерном пространстве и времени декартовую систему координат с осями (x, y,
z, ct). Положение тела в таком 4х-мерном пространстве изображается точкой с
координатами (x, y, z, ct). Эта точка называется мировой точкой. Со
временем она меняет свое положение, описывая в 4х-мерном пространстве
некоторую линию, называемую мировой линией. Даже в том случае, если
тело остается неподвижным в обычном 3х-мерном пространстве, его мировая
точка перемещается вдоль оси ct.
Выберем 2 инерциальные системы отсчета k (x, y, z, t) и k’ (x’, y’, z’, t’).
Будем считать, что система отсчета k’ движется относительно системы k со
скоростью v, направленной вдоль оси OX. Пусть в начальный момент времени
начала этих систем отсчета совпадают. В этот момент из начала отсчета вдоль
оси OX излучается световой импульс. За время t в системе отсчета k он дойдет
до точки ; x = ct ; x’ = ct’
ГАММА (x - vt) = x’ ; ГАММА (x’ – vt’) = x ;
ГАММА (ct - vt) = ct’ УМНОЖАЕМ НА ГАММА (ct + t) = ct ; ПОЛУЧАЕМ
ГАММА (ст.2) (c (ст.2) – v (ст.2)) = c (ст.2);
ГАММА = 1 / [ (корень) 1 – v(ст.2) / c(ст.2) ] ;
В k : x = (x’ + vt’) / (корень) (1-v(ст.2)/c(ст.2)) ; y = y’ ; z = z’
В k’ : x = (x + vt) / (корень) (1-v(ст.2)/c(ст.2)) ; y = y’ ; z = z’
Используем значение ГАММА из предыдущего выражения:
t = (t’ + x’ v/c (ст.2)) / ((корень) 1 – v(ст.2)/ c (ст.2))
t’ = (t + x v/c (ст.2)) / ((корень) 1 – v(ст.2)/ c (ст.2))
--- ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА!!!!!
Они связывают координаты и время в различных инерциальных системах
отсчета. В приделе при c к бесконечности, преобразования Лоренца
17
Постоянное тепловое хаотическое движение приводит к
непрерывному перемещению молекул. При этом если в газе возникают какая либо
неоднородность то со временем все неоднородности выравниваются. Эти процессы
выравнивания не являются хаотическими, а характеризуются определенной
направленностью. Это связано с перемещением характеристик газа от областей с
избытком к областям с недостатком. Существует 3 типа неоднородностей:
1)Неоднородность плотности (концентрации);
2)Неоднородность температуры (энергии);
3)Неоднородность импульса (перемещения) отдельных слоев
движения газа;
Вязкость - Явление вязкости связано с возникновением сил трения
между слоями жидкости или газа, которые перемещаются параллельно друг другу, но
с разными скоростями
S
dy
d
F
Консервативные и неконсервативные силы.
Сила F, действующая на матерьяльную точку называется консервативной или
потенциальной, если работа этой силы по перемещению этого тела из состояния 1 в
состояние 2 не зависит от формы траектории движения, а зависит только от
начального и конечного положения тела. Для консервативной или потенциальной
силы работа по перемещению тела по замкнутой траектории равна нулю.
A = (интеграл с кружком в центре) Fdt=0 – условие потенциальной силы.
В противном случае сила называется диссепативной. Дессипативная сила зависит от
скорости точек и совершает отрицательную работу.
N = dA / dt – мгновенная мощность.
Работа совершается каждый раз, когда энергия одного тела передается
другому или преобразовывается из одного вида в другой. Согласно теореме о
кинетической энергии, работа результирующих сил приводит к изменению
кинетической энергии:
А=K
2
+K
1
= K
18
Постулаты специальной теории относительности. Специальная теория относительности
также как и Ньютоновская механика предполагает, что время однородно, а пространство
однородно и изотопно. В основе специальной теории относительности лежат 2 постулата,
которые являются результатом эксперементально установленных закономерностей.
1 постулат обобщает принцип механической независимости Галилея на все физические
явления. В любых инерциальных системах отсчета все физические явления при одних и тех
же условиях протекают одинакова.
2 постулат выражает принцип имвариантности скорости света. Скорость света в вакууме не
зависит от скорости движения источника. Она одинакова во всех направлениях и во всех
инерциальных системах отсчета. Скорость света в вакууме является предельной скоростью в
природе.
Эйнштейн пересмотрел классические свойства пространства и времени. Он предположил,
что время в различных инерциальных системах отсчета течет неодинаково. Пространство и
время в теории относительности рассматривается совместно, а не обособленно, как в
Ньютоновской механике. Они образуют единое 4х-мерное пространство и время. Возьмем в
таком 4х-мерном пространстве и времени декартовую систему координат с осями (x, y, z, ct).
Положение тела в таком 4х-мерном пространстве изображается точкой с координатами (x, y,
z, ct). Эта точка называется мировой точкой. Со временем она меняет свое положение,
описывая в 4х-мерном пространстве некоторую линию, называемую мировой линией. Даже
в том случае, если тело остается неподвижным в обычном 3х-мерном пространстве, его
мировая точка перемещается вдоль оси ct.
Выберем 2 инерциальные системы отсчета k (x, y, z, t) и k’ (x’, y’, z’, t’). Будем считать, что
система отсчета k’ движется относительно системы k со скоростью v, направленной вдоль
оси OX. Пусть в начальный момент времени начала этих систем отсчета совпадают. В этот
момент из начала отсчета вдоль оси OX излучается световой импульс. За время t в системе
отсчета k он дойдет до точки ; x = ct ; x’ = ct’
ГАММА (x - vt) = x’ ; ГАММА (x’ – vt’) = x ;
ГАММА (ct - vt) = ct’ УМНОЖАЕМ НА ГАММА (ct + t) = ct ; ПОЛУЧАЕМ ГАММА (ст.2)
(c (ст.2) – v (ст.2)) = c (ст.2);
ГАММА = 1 / [ (корень) 1 – v(ст.2) / c(ст.2) ] ;
В k : x = (x’ + vt’) / (корень) (1-v(ст.2)/c(ст.2)) ; y = y’ ; z = z’
В k’ : x = (x + vt) / (корень) (1-v(ст.2)/c(ст.2)) ; y = y’ ; z = z’
Используем значение ГАММА из предыдущего выражения:
t = (t’ + x’ v/c (ст.2)) / ((корень) 1 – v(ст.2)/ c (ст.2))
t’ = (t + x v/c (ст.2)) / ((корень) 1 – v(ст.2)/ c (ст.2))
Уравнения Максвелла не инвариантны относительно законов Галилея. Т.е. в разных
системах отсчета согласно преобразованиям Галилея законы электродинамики должны были
бы описываться различными уравнениями. => Либо Максвелл не прав, либо Галилей не
точен.
Если вместо преобразований Галилея использовать преобразования Лоренца, то
инвариантность законов природы выполняется как для механики, так и для
электродинамики.
R
1
R
2
d
J
0
J
ц.м.
x
S
0
x
V
S
x
y
x
труб
а
y
x
труба
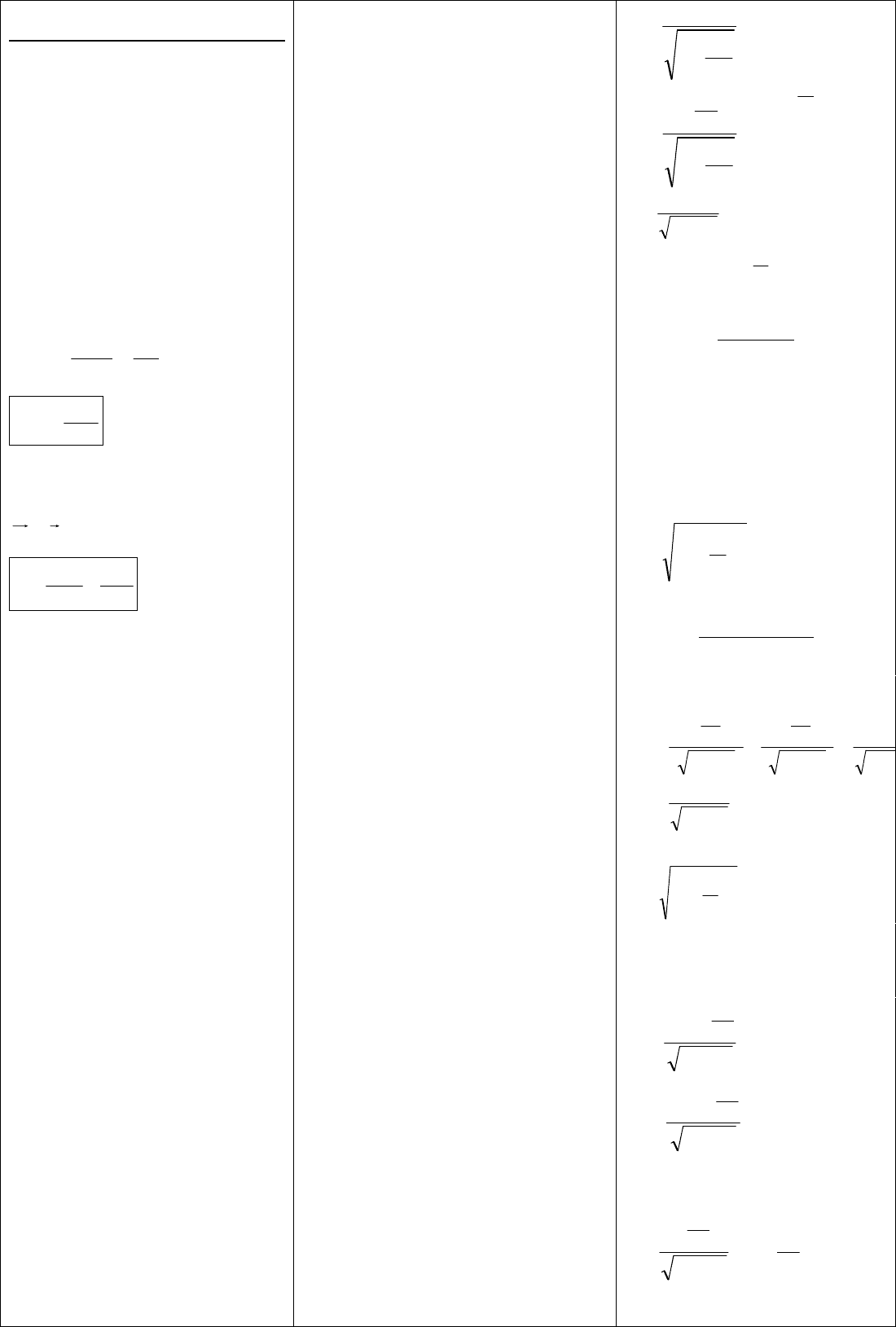
переходят в преобразования Галилея. Различие в течении времени в разных
инерциальных системах отсчета обусловлено существованием предельной
скорости взаимодействий. При малых скоростях движений v0
преобразования Лоренца переходят в преобразования Галилея.
Вращение тела осуществляется тангенсальной составляющей
силой, действующей на тело. Эта же сила совершает работу, величина которой
на dS определяется соотношением:
dA=FdS
учитывая dS=dR, получаем dA=F
Rd
dA=Md
2
1
2
1
MddAA
(при М-const), то
результирующая работа определяется соотношением:
MdMA
2
1
P=dA/dt=M
Кинетическая энергия вращательного тела равна сумме кинетических энергий
его частиц:
i
ii
i
ii
rm
m
K
2
2
2
22
2
2
J
K
ВР
Если тело участвует одновременно в поступательном и
вращательном движении, то скорость его точки будет складываться из
скорости центра масс и линейной скорости:
i
=
C
+
i
(
C
– поступательная скорость центра,
I
– линейная скорость
вращения)
][
1
1
1
R
22
2
2
J
m
K
C
Все силы можно разделить на 3 группы:
1) Внешние
2) Неконсервативные
3) Консервативные
Тогда А
ВН
+A
Н.К
+A
К
=K
Учитывая, что работа консервативных сил может быть выражена через изменение
потенциальной энергии, получаем соотношение:
А
ВН
+A
Н.К
=K+U=E – полная энергия
Таким образом видно, что если система тел замкнута (A
ВН
=0) и отсутствуют
неконсервативные силы (A
Н.К
=0), то E
ПОЛН
=const, K+U=const; K
1
+ U
1
= K
2
+ U
2
;
При наличии неконсервативных сил механическая энергия не
сохраняется. При этом она переходит во внутреннюю энергию теплового хаотического
движения. Если обозначить A
Н.К
= -U
ВНУТР
, то общий вид соотношения: А
ВН
=K+U+U
ВН.
Из последнего соотношения видно, что если система замкнута (А
ВН
=0), то полная энергия остается неизменной:
K+U+U
ВН
=0, K+U+U
ВН
=const
Замкнутая система тел может совершать работу над внешними телами. При этом её
полная энергия уменьшается:
А
ВН
= - А
ВН
` (А
ВН
– Работа внешних сил; А
ВН
`- работа над внешними телами)
Тогда, если система совершает положительную работу над внешними телами, то
изменение полной энергии отрицательно. Последнее утверждение свидетельствует о
том, что вечный двигатель первого рода невозможен.
2
2
2
2
2
1
1
'
c
V
x
c
V
t
t
c
V
Vtx
x
c
V
2
1
1
Из приведенных выражений видно, что при
0
c
V
, преобразования Лоренца
переходят в преобразования Галилея. На основе новых данных Эйнштейн построил
специальную теорию относительности в основе которой лежат 2 постулата:
1) Всеобщий принцип относительности – все законы природы одинаковы во всех
инерциальных системах отсчета.
2) Скорость света c в вакууме одинакова во всех инерциальных системах отсчета (с=3·10
8
м/с)
§6.3 Сокращение длинны .
Пусть некоторый предмет находится в системе S`. Наблюдатель в системе S` измеряя длину
корабля получит:
c
l
l
V
llll
ll
lxxVtxVtxxxl
Vtxx
Vtxx
xxl
2
0
0
12010212
011
022
12
1
)()()(''
)('
)('
''
Наблюдателю в системе S будет казаться, что все предметы в системе S` сокращаются в
направлении движения.
Следствие: Расстояние между точками относительно. В соответствии с принципом
относительности системы S и S` равноправны, поэтому наблюдателю находящемуся в
системе S` также будет казаться, что все предметы в системе S сжимаются => расстояние
между точками относительно.
§6.4 Удлинение промежутков времени.
Пусть в системе S с координатой x
0
произошло 2 события t
1
и t
2
(t
1
-включили прожектор, t
2
-
выключили).
t=t
2
– t
1
Наблюдатель в системе S` измеряя этот промежуток времени по своим часам, получит
величину:
c
t
t
V
tt
t
t
t
tt
c
V
t
c
V
t
t
ttt
2
0
2
22
12
2
0
2
1
2
0
2
2
12
1
1
111
x
1
x
Наблюдателю в системе S` будет казаться, что движущиеся относительно него в системе S
процессы замедляются. Наименьшее значение имеет промежуток времени в той системе
отсчета, в которой события происходят и относительно которой часы находятся в покое. Это
время называют собственным.
Следствие: Относительность понятий одновременности.
Задача: Две молнии ударили в вагон одновременно с позиции наблюдателя в системе S.
(L, t=t
2
–t
1
=0)
''
0
1
))()((''
1
'
1
'
12
2
2
2
2
121212
2
2
2
2
2
2
1
1
tt
c
V
l
c
V
l
c
V
xxttttt
c
V
xt
t
c
V
xt
t
Значит наблюдатель в системе S` сначала увидит молнию передней части вагона и потом
задней.
Распределения Больцмана. Основное уравнение МКТ и максвелские распределения
молекул по скорости были получены предположением, что молекулы равномерно
распределены по объему и все направления движения молекул равномерно распределены по
объему и все направления движения молекул равновероятны. Такие условия могут быть
реализованы только в том случае, если на молекулы не действуют никакие внешние силовые
поля. Однако молекулы любого газа в земных условиях находятся в потенциальном
гравитационном поле Земли, что приводит к нарушению равномерного распределения
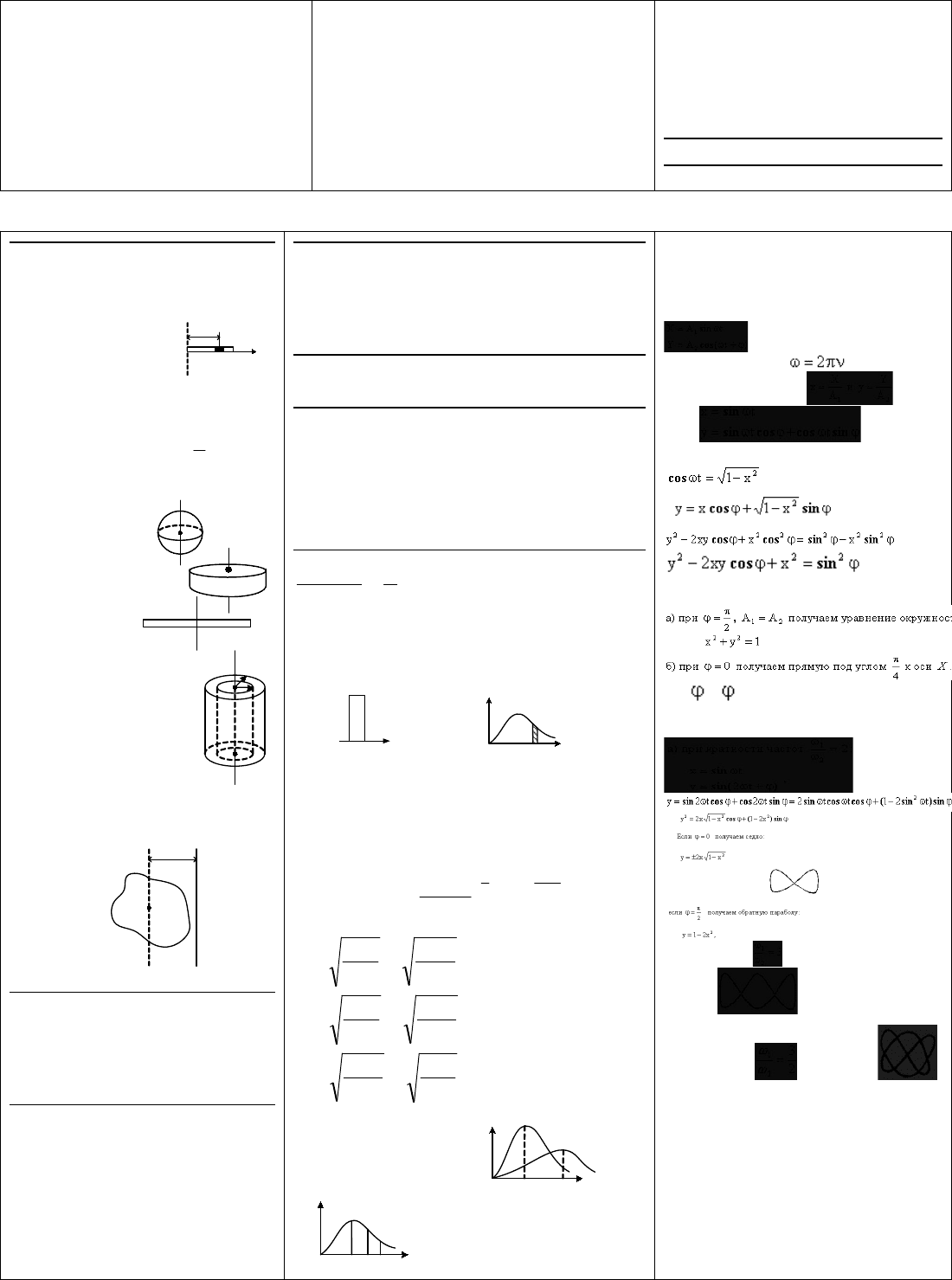
молекул по объему. P = pgh – давление в жидкости ; dP = - pgdh – т.к. с увеличением высоты
давление уменьшается.
PV = mRT / μ => p = m / V = Pμ / RT ; dP = - Pμ g dh / RT = P m0 g dh / kT ; dP/ P = - m0 g dh /
kT ; Проинтегрируем это выражение:
(интеграл P0 - P) dP / P = - (m0 g / kT) (интеграл 0 - h) dh ; ln (P / P0) = - (m0 gh / kT) ; P = R0 e
(ст. m0 gh / kT) ; P = P0 e (ст. – μ n / RT) ; Это выражение описывает распределение частиц
по высоте в гравитационном поле. m0 gh = Wп, поэтому n = n0 e (ст. – Wп / kT). Это и есть
распределения Больцмана. Оно описывает распределение частиц по высоте в
гравитационном поле, а не только в гравитационном поле Земли. Это распределение
приемлемо к частицам, находящимся в состоянии заотического теплового движения.
Дано: m=1кг; p=810
4
Па; =4 кг/м
3
; U-?
Решение: U=5/2m/MRt ; pV=m/M RT p=RT/M=p/ ;
U= 5/2mp/=2.510
4
/4=510
4
Дж
Дано: m
1
=m
2
=m; v
1
=v
2
=v; T
2
/T
1
-? Решение: T=(mv
2
)/2+(Jw
2
)/2; w=v/R;
J
1
=(2/5)mR
2
; J
2
=(1/2)mR
2
; T
1
=(mv
2
)/2+(2/5)mR
2
(v
2
/(2R
2
))=(7/10)mv
2
;
T
2
=(mv
2
)/2+(1/2)mR
2
(v
2
/(2R
2
))=(3/4)mv
2
; T
2
/T
1
=1.07
19
i
ii
rmJ
2
Теорема Штейнера: Момент инерции тонкого стержня
dJ=dmx
2
=m/ L – линейная плотность
dm=dx
dJ= x
2
dx
2
0
2
0
3
1
mldxxdJJ
ll
Моменты инерции тел:
1) Материальная точка J=mR
2
2) Обруч J=mR
2
3) Диск (цилиндр) J=1/2mR
2
4) Шар J=2/5mR
2
5) Тонкий стержень J=1/12mL
2
6) Полый цилиндр J=1/2(R
1
2
+R
2
2
)
Если известен момент инерции относительно оси,
проходящей через центр инерции J
0
, то момент инерции J
относительно другой оси, параллельной первой, можно вычислить по
формуле J=J
0
+ md
2
Первое начало термодинамики или первый закон термодинамики.
dQ = dU + dA ; Теплота, подводимая к термодинамической системе
идет на изменение внутренней энергии и на совершение работы.
Внутренняя энергия U определяется только состоянием
термодинамической системы, а Q и A являются характеристиками
процесса при котором система переходит из одного состояния в
другое. Переход системы из одного состояния в другое может
осуществляться различными путями, поэтому Q и A зависят от способа
перехода системы из одного состояния в другое, в то время, как
внутренняя энергия U определяется только состоянием системы и не
зависит от того, каким путем система перешла в это состояние.
20
Амплитуда, круговая частота, фаза гармонических колебаний.
ν = 1/T – частота ; Циклическая частота – ω = 2ПИ / t = 2ПИv ; S(t)=S(t+T) ;
Гармонические колебания – это колебания по закону sin или cos.
S(t)=A sin(wt + φ0); φ0 – фаза колебаний ; скорость v = Awcos(wt+φ0) ;
u = -Aw(ст.2) sin(wt+φ0) = - w (ст.2) A sin(wt + φ0) = - w (ст.2) S;
d2 S / dt (ст.2) = - w (ст.2) S ; d2 S / dt (ст.2) + w (ст.2) S = 0 ;
Это дифференциальное уравнение описывает гармонические колебания.
Общим решением этого уравнения является S= A1 sinwt+ A2 coswt; A2=S(0)
dS / dt = A1 w coswt + A2 w sinwt ; A1 = (1/w)(dS/dt) при t=0 ; Общее решение можно привести
к виду: S = A sin (wt + φ0), где
A = корень A1(ст.2) + A2(ст.2) ; амплитуда. φ0 = arctg (A2/A1)
Комплексная форма представления колебания.
S=Asin(wt + φ0) = Acos(wt + φ1); φ1 = φ0 – ПИ/2 ; Согласно формуле Эйлера: e (ст. iφ) = cosφ
+ i sinφ; (i – мнимая единица), поэтому гармонические колебания можно записать в
экспоненциальной форме:
S = N e (ст. iwt) = A e (ст. i (wt + φ)) = cos(wt + φ1) + i Asin(wt + φ1)
Сложение гармонических колебаний. Векторная диаграмма.
Графически гармонические колебания можно изобразить с помощью вращающегося вектора
на плоскости: (рисунок – оси OX, OY, вектор, угол между ним и OX равен wt + φ0; под
графиком подпись S = A sin (wt + φ0)).
Графическое представление гармонических колебаний посредством вращающегося вектора
амплитуды A называется методом векторных диаграмм. Рассмотрим с помощью этого
метода сложение 2х одинаково направленных гармонических колебаний, одинаковой частоты
w.
S1 = A1 cos (w0 t + φ1); S2 = A2 cos (w0 t + φ2); S = S1+ S2 = A cos (w0 t + φ)
Используя теорему косинусов можно получить:
A(ст.2)=A1(ст.2) + A2(ст.2) + 2A1 A2 cos (φ2 – φ1) ;
tg φ = (A1 sin φ1 + A2 sin φ2) / (A1 cos φ1 + A2 cos φ2)
1) φ2 – φ1 = + - 2ПИn, n = 0,1,2… A=A1+A2; MAX;
2) φ2 – φ1 = + - (2n +1)ПИ ; A= |A1 – A2|; MIN – это когерентные волны
kT
m
KB
2
3
2
2
0
Введенная ранее средняя квадратичная скорость характеризует среднюю интенсивность
движения, ясно, что при хаотическом движении молекулы движутся с различными
скоростями. Очевидно, что число молекул с очень маленькими скоростями, как и число
молекул со скоростями сравнительно невелико. Основное количество молекул имеет скорости
близкие к
КВ
Распределение по скоростям установил Максвелл. Для этого он ввел функцию
распределения f
(). Физический смысл этой функции заключается в том, что она позволяет
вычислить число молекул dN движущихся со скоростями в интервале (,+d) dN = f
()d
В конечном интервале (1,2):
dfN )(
2
1
12
Графическая зависимость функции распределения от скорости имеет вид:
Аналитический вид:
T
m
T
e
T
m
Nf
2
2
2
3
0
2
)
2
(4)(
(N–общее число
молекул) (m
0
– масса одной молекулы)
RT
m
T 22
0
-наиболее вероятная скорость
RT
m
T 88
0
- средняя арифметическая скорость
0
33
m
kTRT
-
средняя квадратичная скорость.
При увеличении температуры интенсивность
движения возрастает
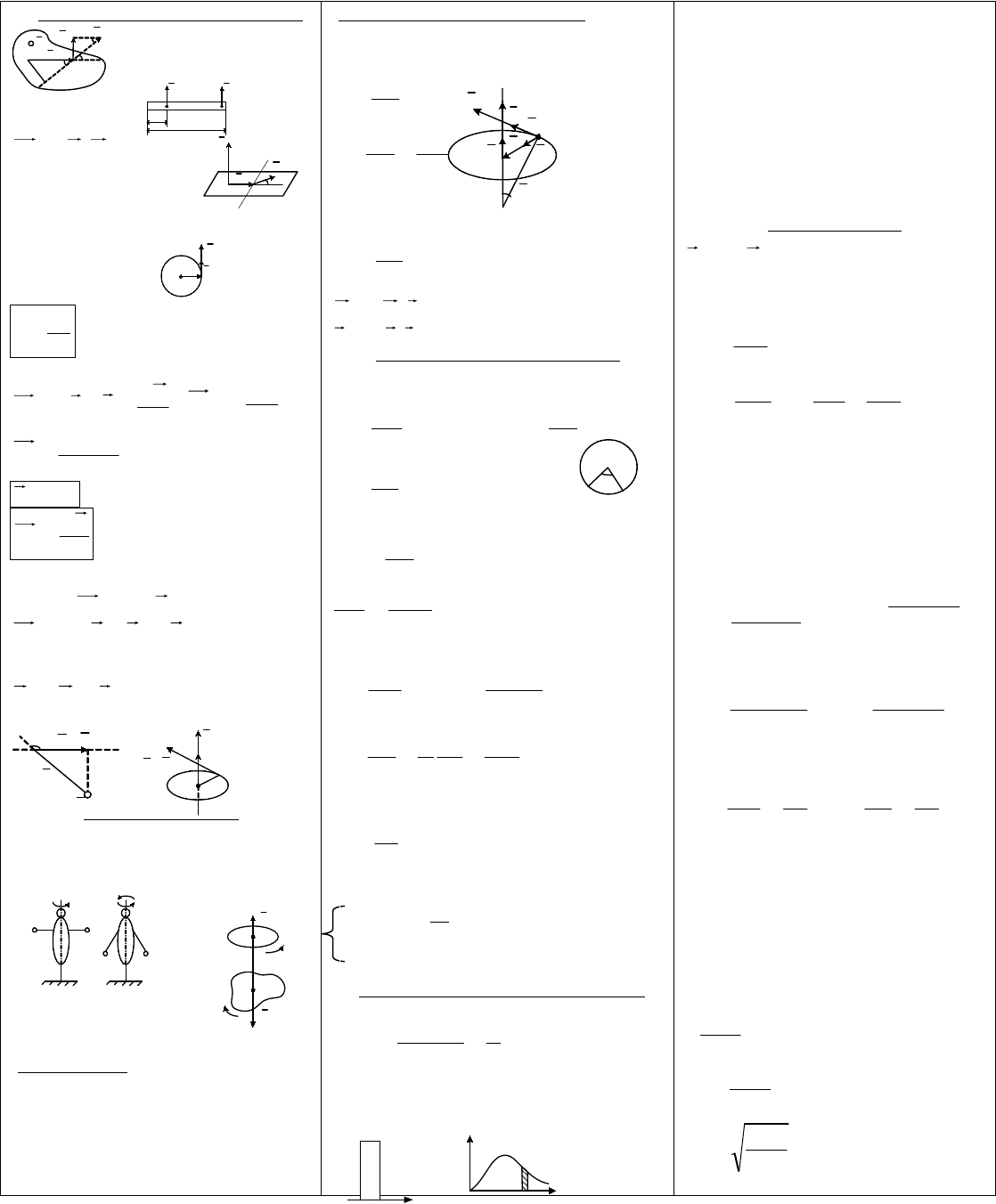
26 1)Фигуры Лиссажу
Фигуры Лиссажу - замкнутые траектории, прочерчиваемые точкой,
совершающей гармонические колебания в двух взаимно
перпендикулярных направлениях. Фигуры Лиссажу можно наблюдать с
помощью осциллографа, подавая одновременно на вход X и вход Y
(горизонтальные и вертикальные отклоняющие пластины) переменные
напряжения кратных частот.
Рассмотрим фигуру:
где - угол сдвига фаз колебаний, - круговая частота
колебаний. Введем новые переменные ,
получаем
Исключая время t, получаем кривую в координатах (x,y) . Из первого
уравнения найдем
и подставим во второе:
.
Возведем обе его части в квадрат, тогда окончательно получаем:
- уравнение эллипса.
В зависимости от значения получаем различно ориентированные эллипсы,
в частности:
Если = (t), то фигуры будут двигаться на экране
осциллографа.
В случае кратных частот колебаний получаем соответствующие фигуры
Лиссажу:
б) при кратности частот получаем фигуру Лиссажу типа короны с
тремя пиками:
в) при кратности частот получаем кардиоиду:
O
O'
0
x
dx
L
R
1
R
2
d
J
0
J
ц.м.
N
dV
N
f
в
с
р
к
в
T
1
t
f
T
2
21
1) 23 Момент силы. 2-й закон Ньютона для вращательного движения.
Опыт показывает, что одна и та
же сила оказывает разное вращательное
действие.
],[ FRM
M=FRsinα
F
τ
=Fsinα
M=F
τ
R
Действие касательной силы на материальную точку может
привести к движению с тангенсальным ускорением:
F
=ma
a=R
F
= mR
F
R=mR
2
M=J
M=F
R
J=mR
2
- момент инерции
J
M
– угловое ускорение
§5.3 Момент импульса точки. 2-й закон Ньютона для вращательного
движения (в другой форме).
JM
dt
d
dt
d
JM
dt
Jd
M
)(
JL
- Момент импульса
dt
Ld
M
- в импульсной форме
Действие момента силы равно скорости изменения момента
импульса
LddtM
(Если M –const)
12
LLLtM
(при М -const)
L=J=mR
2
=mR
2
/R=mR
момент импульса и импульс точки
связаны между собой
],[
mRL
Момент импульса можно определить и относительно начала координат
L=mrsin
Закон сохранения момента импульса.
Из основного закона динамики вращательного движения
следует: если результирующий момент сил равен нулю, соответственно
dL/dt=0, то означает суммарный момент импульса остаётся постоянным.
Таким образом, если на систему не действуют ни ускорение, ни тормозящие
моменты сил, то величина и направление момента импульса остаются
постоянными.
J
1
1
= J
2
2
, если J
1
>J
2
2
>
1
L
1
=L
2
2) Явление переноса в газах.
Постоянное тепловое хаотическое движение приводит к
непрерывному перемещению молекул. При этом если в газе возникают какая
либо неоднородность то со временем все неоднородности выравниваются. Эти
процессы выравнивания не являются хаотическими, а характеризуются
определенной направленностью. Это связано с перемещением характеристик
газа от областей с избытком к областям с недостатком. Существует 3 типа
неоднородностей:
1)Неоднородность плотности (концентрации);
2)Неоднородность температуры (энергии);
3)Неоднородность импульса (перемещения) отдельных слоев
движения газа;
22
1) Кинематические характеристики вращательного движения.
Если точка движется криволинейно, то в каждый момент времени ее
движение может быть представлено как движение по окружности с радиусом R. Ее
движение может быть описано с помощью радиус-вектора, который проведен из (0;0)
в точку, где находится тело:
dt
d
2
2
dt
d
dt
d
RV
Ra
R
R
V
a
n
2
2
R=rsin, V=rsin,
],[ rV
],[ ra
Кинематические характеристики вращательного движения.
Вращательное - движение, когда все точки тела движутся по
концентрическим окружностям, центры которых лежат на одной прямой, которая
называется осью вращения.
ω - угловая скорость, характеризующая быстроту углового перемещен
t
– средняя скорость
dt
d
– мгновенная
скорость
2
2
T
- равномерное угловое вращение;
[ω] = Рад/сек.
R
L
RL
t
R
t
R
R
– линейная скорость вращения
- угловое ускорение, характеризует быстроту изменения угловой скорости.
t
;
dt
d
Связь между характеристикой поступательного и вращательного движения
Radt
d
Rdt
d 11
Ra
R
R
a
н
2
2
Если
-const, то угловой путь и угловая скорость определяется
2
0
2
t
t
t
0
‘+’-равноускоренное движение
2) Распределения Максвелла молекул по скоростям .
kT
m
KB
2
3
2
2
0
Введенная ранее средняя квадратичная скорость характеризует
среднюю интенсивность движения, ясно, что при хаотическом движении молекулы
движутся с различными скоростями. Очевидно, что число молекул с очень
маленькими скоростями, как и число молекул со скоростями сравнительно невелико.
Основное количество молекул имеет скорости близкие к
КВ
Распределение по
скоростям установил Максвелл. Для этого он ввел функцию распределения f
().
Физический смысл этой функции заключается в том, что она позволяет вычислить
число молекул dN движущихся со скоростями в интервале (,+d) dN = f
()d
231) Законы сохранения
Законы сохранения – носят всеобщий характер, они справедливы для всех
видов движения (Механического, теплового, биологического). Закон
сохранения импульса и энергии могут быть строго получены из таких свойств
материи, как однородность пространства и однородность времени.
Однородность пространства означает, что законы физики справедливы в
любой точке пространства. Однородность времени означает, что законы
физики с течением времени не изменяются. Совокупность тел, движение
которых рассматривается совместно и одновременно называется системой тел.
При этом силы, с которыми взаимодействуют тела, принадлежат данной
системе, называются внутренние силы. Силы, которые создаются телами, не
принадлежащими данной системе – внешние силы. Массой системы называют
сумму масс всех тел системы.
i
ii
i
i
mpP
11
Суммарный импульс – сумма импульсов тел системы.
§3.1 Закон сохранения импульса.
constP
i
i
Пусть система состоит из 2-х тел. Согласно 3-у закону Ньютона
F
1
= -F
2
– равны и противоположны по направлению. Согласно 1-у закону
Ньютона действие силы приводит к изменению импульса.
dt
dP
F
1
1
dt
dP
F
2
1
0
21
dt
dP
dt
dP
P
1+
P
2
= P
1
`+ P
2
` = const.
Движение системы тел может быть охарактеризовано понятием центром масс.
Центром масс любой системы тел называется вектор, который определяются
соотношением:
i
i
i
ii
i
m
rm
R
i
i
i
ii
i
m
xm
X
,
i
i
i
ii
i
m
ym
Y
i
i
i
ii
i
m
zm
Z
Скорость движения центра масс:
i
ii
i
i
i
i
i
P
M
m
Mdt
rd
m
Mdt
Rd
111
i
MP
Центр массы системы тел, движущихся, как материальная точка в которой
сосредоточена вся масса системы.
Особенности:
1) F
ВНЕШН.
=0, то dP=0 P=const
2)Если dt 0, то действие внешних сил очень мало dP=0, P=const
3) F
x
=0, dP
x
=0, P
x
=const;
2) Гармонический осциллятор – любая системы описывающаяся
дифференциальным уравнением. (Физический маятник, математический
маятник, колебательный контур)
Примеры:
1) Физический маятник:
J
mga
J
mga
mga
dt
d
J
0
2
2
0
a – расстояние от точки подвеса до
центра масс
R
V
a
a
n
0
r
N
dV
N
J
1
J
2
L
1
L
2
R
2
R
1
0
F
1
F
2
*
F
F
L
0
R
M
F
R
M
a
R
F
L
R
p=m
V
x
L
r
p=m
V
0
L
R
Теплопроводность
Теплопроводность – явление переноса энергии без переноса
вещества. Определим изменение температуры с помощью градиента
температуры.
0
12
12
xx
TT
x
T
Количество энергии, которое переносится через площадку за
время t, определяется уравнением Фурье:
St
X
T
Q
где
V
C
3
1
В конечном интервале (1,2):
dfN )(
2
1
12
Графическая зависимость функции распределения от скорости имеет
вид:
Аналитический вид:
T
m
T
e
T
m
Nf
2
2
2
3
0
2
)
2
(4)(
(N–общее
число молекул) (m
0
– масса одной молекулы)
RT
m
T 22
0
-
наиболее вероятная скорость
RT
m
T 88
0
-
средняя арифметическая скорость
0
33
m
kTRT
- средняя квадратичная скорость.
При увеличении температуры интенсивность движения возрастает
2) Математический маятник:
g
l
T
xx
mlJ
2
0
2
0
2
Физический маятник – тело способное совершать колебания относительно
неподвижной оси проходящей через цент масс
M= –F
τ
a= –mgaα
k=mga
a – расстояние от 0 до центра центра масс
Пружинный маятник:
F= –kx
24
1) законы Ньютона. Динамика – раздел механики, в котором
изучаются причины возникновения или изменения в движении тел. В основе
лежат 3 закона Ньютона.
1-й закон Ньютона: Если на тело не действуют другие тела,
или их действие скомпенсировано, то тело находится в состоянии покоя или в
состоянии равномерного прямолинейного движения. Состояние покоя или
состояние равномерного прямолинейного движения – это природное свойство
всех тел – это свойство называется инертностью. Системы отсчёта, в которых
выполняется 1-й закон Ньютона, называются инерциальными системами
отсчёта.
Все инерциальные системы отсчета
движутся друг относительно друга равномерно и
прямолинейно. Системы отсчета, в которых тела
движутся с ускорением, называются
неинерциальными.
2-й закон Ньютона.
2-й закон Ньютона: Ускорение, которое приобретает тело
прямо пропорционально результирующей всех сил, действующих на тело и
обратно пропорционально массе.
m
F
a
,
.......
21
FFF
Силой называется векторная физическая величина, которая характеризует
действие одного тела на другое.
2
21
r
mm
GF
2
21
r
qq
kF
Импульсная форма 2-го закона Ньютона.
dt
md
dt
d
mamF
mP
dt
Pd
F
– 2-й закон Ньютона - общая формулировка
PddtF
Действие силы в течении t приводит к изменению импульса тела. Если F-
const
FΔt=ΔP
3-й закон Ньютона (Закон взаимодействия тел).
3-й закон Ньютона: два тела взаимодействуют друг с
другом с силами, равными по величине и по модулю, но
противоположными по направлению
Силы прилаженные к разным телам и никогда не могут
компенсировать друг друга
2) Реальные газы§15.1 Межмолекулярные
силы.
Наличие межмолекулярных взаимодействий
приводит к появлению новых свойств, который
существенным образом отличаются от свойств
идеального газа.
U – потенциал взаимодействия,
r – расстояние,
r
0
– равновесное расстояние.
25 1) Механическое движение. Системы отсчёта. Физические модели.
Механическое движение – изменение положения тел друг относительно друга с течением
времени. Для описания механического движения необходима система отсчёта. В неё входят: тело
отсчёта, система координат, прибор для измерения времени.
Физические модели:
1) Материальная точка – тело, размерами которого можно пренебречь.
2) Абсолютно твёрдое тело – тело, состоящее из совокупности материальных точек, жестко
связанных между собой.
Существует два вида механических движений:
1) Поступательное – движение, когда все точки тела движутся по одинаковым траекториям и
любая прямая, проведенная внутри тела остается параллельная сама себе.
2)Вращательное - движение, когда все точки тела движутся по концентрическим окружностям,
центры которых лежат на одной прямой, которая называется осью вращения.
§1.2 Уравнение движения.
При движении материальная точка описывает некоторую линию, т. о. положению точки и
соответствует радиус-вектор, который и является функцией времени. Уравнение движения –
функция, дающая возможность определить положение точки в любой момент времени.
Уравнения движения: 1)
a
=const
2
2
0
0
ta
txx
x
x
2
2
00
ta
tyy
y
н
2) x(t)=Acos(ωt + φ);
2
2
0
at
tS
Траектория (путь), Перемещение(Вектор)
t
r
мгн
t
x
x
t
y
y
мгн
– всегда касательная к траектории.
t
S
ср
dt
dS
мгн
2) Круговым процессом или циклом называется такой в результате которого
термодинамическая система возвращается в исходное сост. Из рисунка видно что работа
2
1
0
V
V
a
pdVA
0
1
2
V
V
b
pdVA
baba
AAAAA
ba
AA
- прямой цикл;
ba
AA
-
обратный цикл
0U
AQ
26
1) Сложение перпендикулярных колебаний. Конический маятник.
x=A
1
cos(ωt+φ
01
)
y=A
2
cos(ωt+φ
02
)
1) φ
01
=φ
02
=0
x
A
A
y
1
2
- движение вдоль прямой.
2) φ
01
=0, φ
02
=π/2
y=A
2
cos(φt+π/2)=A
2
sin(ωt)
1
2
2
2
2
1
2
A
y
A
x
Сложные функции описывающие движение – фигуры Лиссажу
2) Барометрическая формула.
Распределение молекул в поле силы тяжести является неравномерным. В
жидкостях давление на различных глубинах различно в следствии
гидростатического давления.
)(
1221
hhgpp
hgppp
12
Для газов это соотношение может быть записано только для малых толщин:
gdhdp
RT
M
m
pV
RT
M
p
RT
pM
т.о.
gdh
RT
pM
dp
dh
RT
Mg
p
dp
p
p
p
p
p
p
ppp
p
dp
0
0
0
0
lnlnlnln
h
h
RT
Mg
dh
RT
Mg
0
)(
т.о.
h
RT
Mg
p
p
0
ln
h
RT
Mg
e
p
p
0
h
RT
Mg
epp
0
kT
ghm
epp
0
0
- барометрическая формула. Вывод получен при
условии, что температура на всех высотах одинакова.
§12.4 Распределение Больцмана .
Распределение Больцмана – распределение частиц в потенциальном поле.
Барометрическая формула является частным случаем распределения частиц в
f
в
ср
кв
T
1
t
f
T
2
mg
N
F
N
m
g
mg
F
F
m
g
y
=-kx
F
F
т
р
F
1
F
2
F
1
F
2
N
mg
P
0
a
F
ц.м.
mg
F
у
x
y
x
m
1
m
2
m
3
r
1
r
2
r
3
U
r
r
0
0
U
m
y
x
x
y
y
x
x
y
V
0
P
1
2
a
b
y
x
V
0
g
h
y
x
y
0
x
0
V
0
(
t
r, )
r
r
(t)
r
(t+
t)
r
S
0
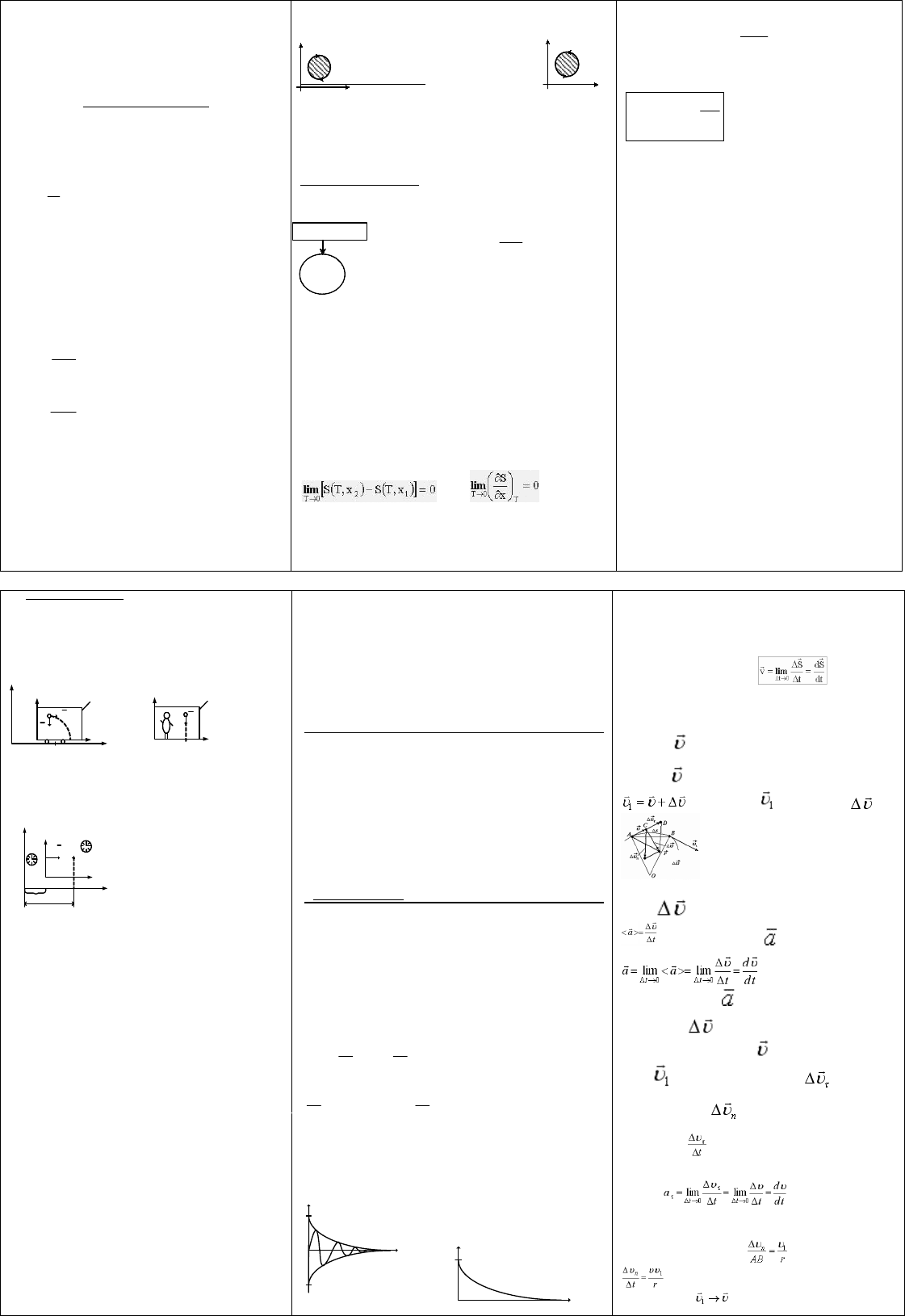
Если значение минимального потенциала существенно меньше энергии
теплового движения, то вещество находится в газообразном состоянии. Если
это значение имеет порядок kT, то это соответствует жидкому состоянию.
Если энергия взаимодействия существенно превосходит энергию теплового
движения то это соответствует твердому состоянию вещества.
kTU
min
– газ,
kTU ~
min
– жидкость,
kTU
min
- твердое тело.
§15.2 Уравнение Ван-дер-Ваальса.
Учет межмолекулярных взаимодействий был произведен впервые
голландским физиком Ван-дер-Ваальсом. При этом он исходил из простой
модели, которая была основана на следующих положениях:
1)Молекулы газов представляют собой шары с эффективным диаметром.
2)Между молекулами существуют только силы притяжения
3)Силы отталкивания учтены введением эффективного диаметра.
Учет собственного объема молекулы
3
6
1
dV
приводит к тому, что «Свободный» молярный объем
в сосуде уменьшается по сравнению с идеальным газом на величину b,
bVV
*
, где b – постоянная Ван-дер-Ваальса
vrNb
A
Наличие сил притяжения между молекулами
реального газа приводит к тому, что давление становится меньше на
некоторую величину p*.
Таким образом
*
ppp
ид
Величина P* согласно теории
Ван-дер-Ваальса обратно пропорциональна квадрату объема:
2
*
V
a
p
, т.о. уравнение состояния имеет вид:
RTbV
V
a
p ))((
2
Для разреженных газов
размерами атомов можно пренебречь. Уравнение Ван-дер-Ваальса переходит
в обычное уравнение Менделеева-Клапейрона.
Важное значение круговых процессах является то, что система возвращается в
исходное состояние, Следовательно U=0, Q=A т.е. Работа совершается за счет подводимой
теплоты. Круговые процессы являются основой всех тепловых машин. кот бывают 2-х типов
1)Реализующие прямой цикл Q=A>0, т.е. тепло
мех. раб.
2)Реализующие обратный цикл
Q=A<0, т.е. мех. раб. тепло
Обратимые и необратимые процессы.
Обратимыми называют ТД процессы в которых осуществляется переход из
конечного состояния в начальное через те же промежуточные состояния, что и в прямом
процессе. Можно доказать, что обратимыми являются только равновесные процессы. (В реальной
жизни таких процессов нет)
Вывод: любые реальные самопроизвольные процессы необратимы. Примеры:
При соединении 2-х систем с разными температурами происходит теплопередача, в результате
которой энергия передается от более нагретого тела к менее нагретому. Если эта система
замкнута, то через некоторое время, температуры этих тел выровняются. Система переходит в
состояние теплового равновесия, которое характеризуется вполне определённой температурой T.
Такой процесс также является необратимым. Самопроизвольно одно тело не может принять
температуру большую, а другое меньшую.
§14.7 Второй закон термодинамики.
Невозможен процесс результатом которого является превращение всей теплоты
полученной от нагревателя в эквивалентную механическую работу. Другими словами этот закон
эквивалентен утверждению о невозможности вечного двигателя 2-го рода. Схема вечного
двигателя 2 рода:
%100*
1
Q
A
Следствие: 1)2-й закон Термодинамики запрещает
использовать энергию системы находящейся в
термодинамическом равновесии.
2)Для преобразования тепловой энергии должны быть две
системы находящееся при разных температурах. Невозможно преобразование всей энергии
теплового, хаотического движения в упорядоченную энергию мех. движения. Возможно лишь
частичное преобразование внутренней энергии и только при наличии двух систем не
находящихся в тепловом равновесии. Другая часть энергии передается холодильнику.
Преобразование внутренней энергии теплового хаотического движения в мех. работу в
термодинамике характеризуется двумя величинами, которые наряду с внутренней энергией
являются функциями состояний системы. Это: F-свобод. энергия. S–энтропия. Все 3 функции
состояния связаны соотношением
U=F+TS
Свободная энергия та часть внутренней энергии, которая может быть преобразована в
механическую энергию.
(TS) - связанная энергия – это та часть, которая не может быть преобразована в механическую
энергию.
Теорема Нернста
При абсолютном нуле температуры любые изменения состояния происходят без изменения
энтропии.
Но абсолютный ноль T = 0 температуры недостижим, т.к. иначе был бы возможен вечный
двигатель второго рода η = 1 −Т
2
/Т
1
= 1 .
Для равновесных систем: при T → 0 энтропия S не зависит от значения любого параметра
системы. По 2-му началу термодинамики:
или
Доказательство недостижимости абсолютного нуля T = 0 из 3-го начала термодинамики:
Охлаждение системы осуществляется повторением последовательно процессов адиабатического
расширения (для снижения T) и изотермического сжатия (для уменьшения S). Но при T → 0
энтропия S перестаёт изменяться, а приобретает некоторое постоянное значение (принятое за
ноль!). Поэтому за конечное число циклов состояние с S = 0 недостижимо, следовательно,
недостижим и абсолютный ноль температуры: к абсолютному нулю температуры T → 0 можно
лишь асимптотически приближаться.
потенциальном поле. Преобразуем его используя уравнение Менделеева-Клапейрона
в виде: p=nkT
kT
ghm
kTennkT
0
0
ghmW
П 0
kT
W
П
enn
0
-распределение Больцмана.
Анализ:
1)T ∞, следовательно W
П
/kT 0, n=n
0
2)T 0, след. W
П
/kT ∞, n 0, Все молекулы падают на землю.
Барометрическая формулаопределяет зависимость давления или плотности газа от
высоты в поле тяжести.
Для идеального газа, имеющего постоянную температуру Т и находящегося в
однородном поле тяжести (во всех точках его объёма ускорение свободного падения
g одинаково), Б. ф. имеет следующий вид:
р = p0exp [-gm.(h - h0)/RT]???? (1),
где р - давление газа в слое, расположенном на высоте h, p0 - давление на нулевом
уровне (h = h0), m - молекулярная масса газа, R - газовая постоянная, Т - абсолютная
температура. Графически зависимость (1) представлена на рис. Из Б. ф. (1) следует,
что концентрация молекул n (или плотность газа) убывает с высотой по тому же
закону:
n =n0exp [-mg (h-h0)/kT],
где m - масса молекулы, k - Больцмана постоянная.
Б. ф. может быть получена из закона распределения молекул идеального газа по
скоростям и координатам в потенциальном силовом поле (см. Больцмана статистика).
При этом должны выполняться два условия: постоянство температуры газа и
однородность силового поля. Аналогичные условия могут выполняться и для
мельчайших твёрдых частичек, взвешенных в жидкости или газе. Основываясь на
этом, французский физик Ж. Перрен в 1908 применил Б. ф. к распределению по
высоте частичек эмульсии, что позволило ему непосредственно определить значение
постоянной Больцмана.
Б. ф. показывает, что плотность газа уменьшается с высотой по экспоненциальному
закону. Величина -mg (h-h0)/kT, определяющая быстроту спада плотности,
представляет собой отношение потенциальной энергии частиц к их средней
кинетической энергии, пропорциональной kT. Чем выше температура Т, тем
медленнее убывает плотность с высотой. С другой стороны, возрастание силы
тяжести mg (при неизменной температуре) приводит к значительно большему
уплотнению нижних слоев и увеличению перепада (градиента) плотности.
Действующая на частицы сила тяжести mg может изменяться за счёт двух величин:
ускорения g и массы частиц m.
Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной
массы по-разному распределяются по высоте.
Реальное распределение давления и плотности воздуха в земной атмосфере не
следует Б. ф., т.к. в пределах атмосферы температура и ускорение свободного
падения меняются с высотой и географической широтой. Кроме того, атмосферное
давление увеличивается с концентрацией в атмосфере паров воды.
Б. ф. лежит в основе барометрического нивелирования - метода определения разности
высот Dh между двумя точками по измеряемому в этих точках давлению (p1 и p2).
Поскольку атмосферное давление зависит от погоды, интервал времени между
измерениями должен быть возможно меньшим, а пункты измерения располагаться не
слишком далеко друг от друга. Б. ф. записывается в этом случае в виде: Dh = 18400Ї
(1+at) lg (p1/p2) (в м), где t - средняя температура слоя воздуха между точками
измерения, a ?- температурный коэффициент объёмного расширения воздуха.
Погрешность при расчётах по этой формуле не превышает 0,1-0,5% от измеряемой
высоты. Более точна формула Лапласа, учитывающая влияние влажности воздуха и
изменение ускорения свободного падения.
27 1) Преобразования Галилея.
Все законы классической механики одинаковы во всех инерциальных
системах отсчета. Значит, все инерционные системы отсчета равноправны и не
возможно выявить какую-то главную систему отсчета. Отсюда следует, что
если наблюдатель находится в какой-либо инерциальной системе отсчета, то с
помощью экспериментов он не может определить движется он или нет. Всякое
движение в механике описывается в той или иной системе отсчета по-разному.
Н
айдем взаимосвязь между координатами, измеренными в
разных системах отсчета:
Пусть в начальный момент времени начала
координат S и S` совпадают. Тогда через t
координаты точки P которая движется вместе с
системой S` будут (S`–x`, S – x).
Из рис. видно что
.одинакого) ттече(ввремt t
yy
tV-xx
tt
Vtrr
Преобразования
Галилея
С помощью этого преобразования координат, зная уравнения движения в
одной системе, можно получить уравнение движения в другой инерциальной
системе.
Следствии:
Длина отрезка во всех инерциальных системах отсчета
одинакова.
LL` Lx-xVt)-(x - Vt)-(x''-xxL'
121212
Интервал времени одинаков:
tttttttt ' ''
121
2
Проекции скоростей измеренных в разных системах
складываются алгебраически:
28
1) Масса – мера количества вещества. F=ma, F=G * m1 * m2 * / R*R
Импульс тела – количество движения. P = m v (вектор) – справедливо для
матерьяльной точки. Если тело имеет конечный размер, то импульс этого тела можно
найти как векторную сумму импульсов матерьяльных точек, на которое можно
разбить это тело. P – импульс.
Сила – мера взаимодействия тел друг с другом. 4 вида взаимодействий:
1. Гравитационное – взаимодействие притяжения 2х тел, обладающих массой.
2. Слабые взаимодействия – ответственно за некоторые виды распада элементарных
частиц, в частности за бета-распад.
3. Электро-магнитные взаимодействия – кулоновская и лоренцева силы.
4. Сильное взаимодействие – обеспечивает связь нуклонов в ядре. Закон всемирного
тяготения:
F=G m1 m2 / R * R; Fk = (1 / 4ПИ * Rнулевое) * (E1 E2 / R * R);
Fл = kq[v,b (векторы)]
Моментом импульса (моментом количества движения) матерьяльной точки
относительно оси называется векторная величина L = r * P ; где все величины –
векторы ; r – расстояние от оси вращения до этой точки. Импульс точки: P = mv.
Моментом силы M называется величина M=r *F
Моментом импульса твердого тела относительно оси является
L = сумма ri Pi ; |L| = |r | |P| sinАЛЬФА ; Рассмотрим случай, когда АЛЬФА=ПИ/ 2: L =
сумма mi vi ri = w сумма mi vi (ст.2) = J w; L = J w ;
Продефференцируем это выражение по времени: dL / dt = J dw/dt = J центромасс = M ;
dL / dt = M ; Если M= 0, то dL / dt = 0 L = const
Это закон сохранения импульса!!! --- Если на систему тел не действует момент силы
M или равнодействующая всех сил равна нулю, то момент импульса этой системы
остается постоянным. Закон сохранения момента импульса является
фундаментальным законом физики. Он справедлив не только в классической
механике, но и в релитивистской и в квантовой механике. Закон сохранения момента
импульса связан с изотропностью пространства – пространство обладает
одинаковыми свойствами во всех направлениях.
2) Затухающие колебания.
Колебания с течением времени затухают. Это связано с тем, что действуют силы
сопротивления, которые при малых скоростях пропорциональны скорости.
xrrVF
kxF
c
Таким образом, 2-й закон Ньютона записывается в виде:
02
2
0
2
0
2
0
xxx
m
r
m
k
x
m
k
x
m
r
x
xrkxxm
Полученное дифференциальное уравнение называется дифференциальным
уравнением затухающих колебаний.
Решением является функция:
29
1) Средняя скорость движения: скалярная - отношение пути к промежутку
времени, в течение которого материальная точка прошла этот путь Vср = L /
Δt, векторная - отношение перемещения точки к промежутку времени, в
течении которого точка совершила перемещение .
Мгновенная скорость - величина, равная пределу средней векторной скорости
при уменьшении промежутка времени [м / с]
В случае неравномерного движения важно знать, как быстро изменяется
скорость с течением времени. Физической величиной, характеризующей
быстроту изменения скорости по модулю и направлению, является
ускорение.
Пусть вектор задает скорость точки А в момент времени t. За время
Dt движущаяся точка перешла в положение В и приобрела скорость,
отличную от как по модулю, так и направлению, равную
. Перенесем вектор в точку А и найдем .
— Средним ускорением неравномерного движения в интервале от t до
t+Dt называется векторная величина, равная отношению изменения
скорости к интервалу времени Dt:
— Мгновенным ускорением (ускорением) материальной
точки в момент времени t будет предел среднего ускорения:
Таким образом, ускорение есть векторная величина, равная первой
производной скорости по времени.
Разложим вектор на две составляющие. Для этого из точки А (см.
рисунок) по направлению скорости отложим вектор AD, по модулю
равный . Очевидно, что вектор CD, равный , представляет
собой изменение скорости по модулю за время Dt:Dut = u1 – u. Вторая же
составляющая вектора характеризует изменение скорости за
время Dt по направлению.
Предел отношения , являющийся производной от скорости по времени,
определяет быстроту изменения скорости в данный момент времени t и
является тангенциальной составляющей ускорения at (для прямолинейного
движения a)
Определим вторую составляющую ускорения. Допустим, что точка В
достаточно близка к точке А, поэтому Ds можно считать дугой окружности
некоторого радиуса r, мало отличающейся от хорды АВ. Тогда из подобия
треугольников АОВ и EAD следует , но так как АВ = u Dt, то
В пределе при Dt ®0 .
V
0
P
V
0
P
нагреватель T
1
рабочее
тело
Q
1
=> A=Q
1
y
x
V
x
V
y
S
S'y'
x'
x
0
V
y'
S'
y'
x'
x'
0
Vt
y
x
S
S'
y'
x'
x
0
x'
0
t'
t
p
V
0
A
t
A
0
A
t
A
0
-A
0
