Ответы на экзамен (2 семестр)
Подождите немного. Документ загружается.


VVV
VVV
V
dt
dx
td
Vdtdx
td
d
ddxdx
tddtVtxx
xx
xx
'
'
)(x'
tV-'
'
Законы классической физики инвариантны относительно
преобразований Галилея:
''
'
'
)()()(
2
2
'
'
'
rmF
rmF
rr
xx
x
dt
xd
x
dt
dx
aa
V
dt
d
V
td
d
V
td
d
VVV
xx
xx
xx
Уравнение динамики и все типы законов сохранения во всех
системах отсчета имеют одинаковый вид. Поэтому говорят, что все законы
механики инвариантны относительно преобразований Галилея.
Инвариантность уравнений Ньютона относительно преобразований Галилея
является математическим выражением классического принципа
относительности. (Все инерционные системы равноправны)
2) Энтропия – является функцией состояния. Ее изменение связано с
получением и отдачей теплоты. Элементарное изменение энтропии при
заданной температуре определяется соотношением.
T
dQ
dS
Поскольку энтропия является функцией состояния
0
dT
dQ
S
Можно показать, что любой процесс приводит к возрастанию
энтропии S>=0. Если термодинамическая система не является замкнутой т.е.
имеется внешнее воздействие, то энтропия может и убывать. Найдем
изменение энтропии в процессах связанных с идеальным газом.
2
1
2
1
12
T
dA
T
dU
T
dQ
S
dTc
M
m
RdT
i
M
m
dU
V
2
V
dV
RT
M
m
pdVdA
2
1
2
1
12
V
dV
R
T
dT
c
M
m
SSS
v
1
2
1
2
lnln
V
V
R
T
T
c
M
m
S
V
При
constT
1
2
ln
V
V
R
M
m
S
При
constV
1
2
ln
T
T
c
M
m
S
v
При
0dQ
0S
Энтропия системы тел равна сумме энтропий каждого из них.
Пример: Найти
S
cmdTdQ
2
1
1
2
2
1
ln
T
T
T
T
cm
T
dT
cm
T
dQ
S
T
m
T
Q
dQ
TT
dQ
S
1
- при
плавлении и испарении;
22
0
ω
0
– частота свободных колебаний
– коэффициент затухания.
При больших возможно, что =0: Апериодический процесс. В этом случае,
энергия, полученная от отклонения, полностью расходуется на преодоление сил
сопротивления.
Характеризуется логарифмическим декрементом:
T
T
eAtA
TtA
tA
t
1
2
)(
)(
)(
ln
0
Уравнение, описывающее затухающие колебания:
(d2 x / dt (ст2)) + b/m * dx/dt + kx / m = 0 ; Введем обозначения:
w 0 (ст.2) = k/m ; b/m = 2БЕТА ; БЕТА = b/2m; b – коэффициент сопротивления ; (d2
x / dt (ст.2)) + 2БЕТА*dx/dt + w 0 (ст.2) x = 0 ;
БЕТА – коэффициент затухания.
Общее решение этого уравнения будем искать в виде X = A e (ст.ЛЯМДА t).
Подставим это решение в дифференциальное уравнение затухающих колебаний: dx/dt
= A ЛЯМДА e (ст. ЛЯМДА t) ; d2 x / dt (ст.2) = A ЛЯМДА (ст.2) e (ст. ЛЯМДА t); A
ЛЯМДА (ст.2) e (ст. ЛЯМДА t) + 2bA ЛЯМДА e (ст.ЛЯМДА t) + w 0 (ст.2) A e
(ст.ЛЯМДА t) ; Сокращаем:
ЛЯМДА (ст.2) +2БЕТА d + w 0 (ст.2) = 0 – характеристическое уравнение.
Решая его, получаем: X = - БЕТА + - (корень БЕТА (ст.2) – w 0 (ст.2)) =
- БЕТА + - i (корень w 0 (ст.2) – БЕТА (ст.2)) ; Таким образом общее решение
исходного дифференциального уравнения можно преобразовать к виду: w = (корень
w 0 (ст.2) – БЕТА (ст.2)) ; X (t) = A0 e (ст. – БЕТА t) sin (wt + φ 0) ;
(рисунок – график затухающих колебаний – сжатый синус, все ниже и неже стает по
оси OY).
Затухающие колебания не являются периодическими, т.к. максимальное значение
колеблющихся величин, достигаемое в некоторый момент времени в последующем
никогда не повторяется, поэтому можно говорить об условном периоде затухающих
колебаний – T = 2ПИ / w = 2ПИ / (корень w 0 (ст.2) – БЕТА (ст.2)). Если БЕТА >= w
0, то процесс становится апериодическим.
Логарифмический декремент затухания.
δ = ln (A(t) / A(t + ПИ)) = ln (A0 e (ст. – БЕТА t) / A0 e (ст. – БЕТА (t + ПИ))) = ln (A0 e
(ст. – БЕТА t) / A0 e (ст. – БЕТА t) e (ст. – БЕТА ПИ)) = БЕТА T ;
δ = БЕТА T = 1 / N ; Время релаксации (ТАУ) в течении которого амплитуда
затухающих колебаний убывает в e раз ; A = A0 / e = A0 e (ст. – БЕТА ТАУ) ; e (ст. -
1) = e (ст. – БЕТА ТАУ) – БЕТА ТАУ = 1 ;
ТАУ = 1 / БЕТА ; N = ТАУ / T – число колебаний, в течении которых амплитуда
убывает в e раз ; δ = 1 / N ;
Поскольку , угол EAD стремится к нулю, а так как треугольник
EAD равнобедренный, то угол ADE между и стремится к
прямому. Следовательно, при Dt®0 векторы и оказываются
взаимно перпендикулярными. Так как вектор скорости направлен по
касательной к траектории, то вектор , перпендикулярный скорости,
будет направлен к центру круга ее кривизны.
Вторая составляющая ускорения, равная
2) Идеальная тепловая машина Карно.
В ее основе лежит круговой процесс который
называется циклом Карно
1-2: A
1
=Q
1
>0 – Изотерм. расширение
2-3: Q=0 – Адиабатическое расширение;
3-4: A
2
=Q
2
<0 – Изотермическое сжатие;
4-1: Q=0 Адиабатическое сжатие.
Для замкнутых циклов работа совершаемая
газом в цикле Карно равна подводимому
теплу. Тепловая машина реализующая этот цикл имеет максимальный КПД по
сравнению с любым другим циклом. =(T
1
-T
2
)/T
1
; Для повышения КПД
тепловых машин Необходимо увеличивать температуру нагревателя и
уменьшать температуру холодильника. КПД любой реальной тепловой всегда
меньше, чем у машины Карно:
1
21
1
21
Q
QQ
T
TT
§14.6 Обратимые и необратимые процессы.
Обратимыми называют ТД процессы в которых осуществляется переход из
конечного состояния в начальное через те же промежуточные состояния, что и
в прямом процессе. Можно доказать, что обратимыми являются только
равновесные процессы. (В реальной жизни таких процессов нет)
Вывод: любые реальные самопроизвольные процессы необратимы. Примеры:
При соединении 2-х систем с разными температурами происходит
теплопередача, в результате которой энергия передается от более нагретого
тела к менее нагретому. Если эта система замкнута, то через некоторое время,
температуры этих тел выровняются. Система переходит в состояние теплового
равновесия, которое характеризуется вполне определённой температурой T.
Такой процесс также является необратимым. Самопроизвольно одно тело не
может принять температуру большую, а другое меньшую.
V
0
P
1
2
3
4
Q
1
Q
2
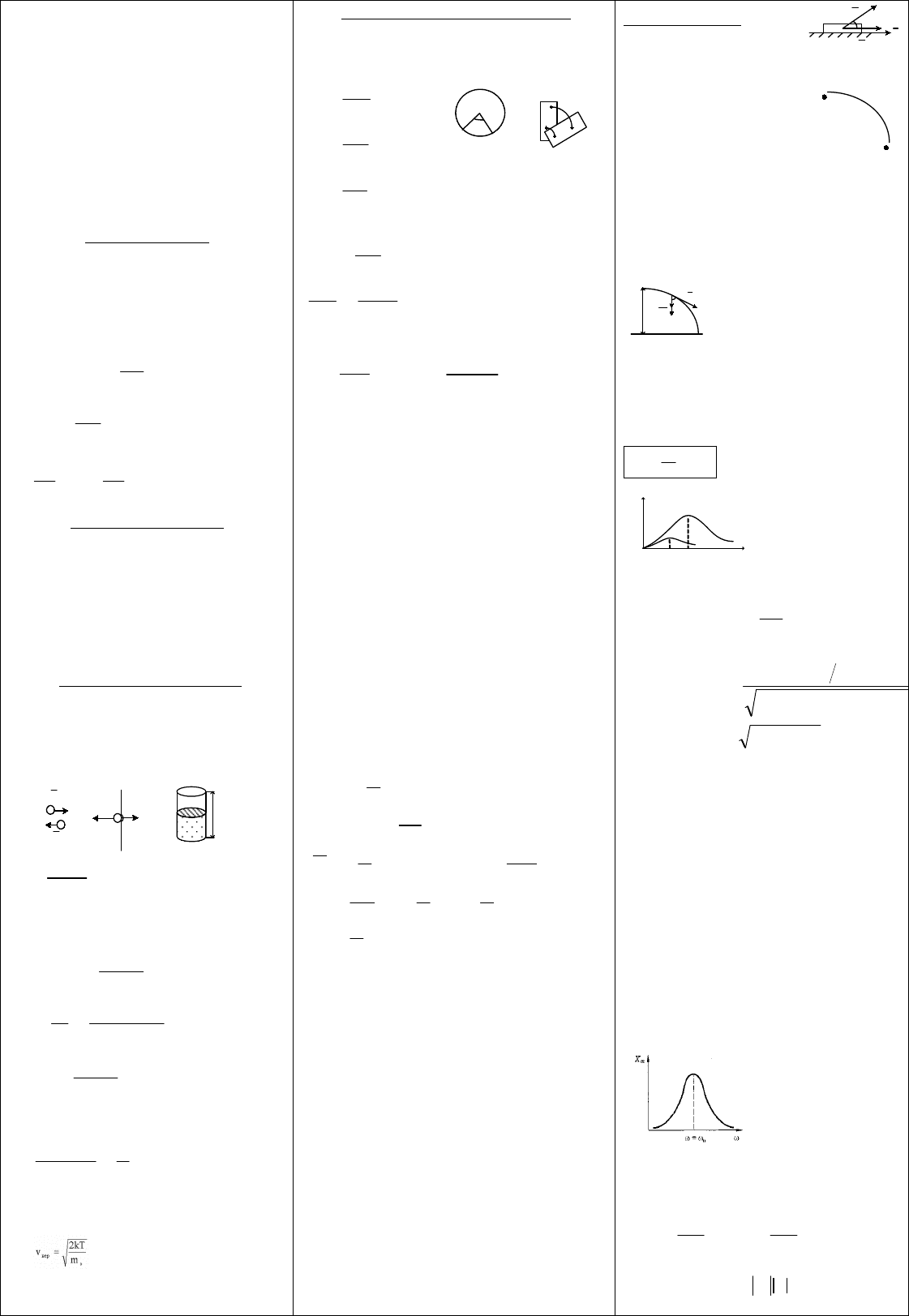
30 1)Потенциальная энергия. Работа, совершаемая потенциальными силами
при изменениии конфигурации системы, т.е. расположении ее частей
относительно системы отсчета не зависит от пути перехода из начального
состояния в конечное. Эта работа A1-2 определяется только начальной и
конечной конфигурацией систем, следовательно ее можно представить в виде
разности значений некоторой функции конфигурации системы, называемой
потенциальной энергией Wп. A1-2= Wп (1) – Wп (2) ;
dA= - dWп. В каждой конкретной задаче для получения однозначной
энергетической зависимости каждой потенциальной рассматриваемой
системы от ее конфигурации, выбирают нулевую конфигурацию, в которой
потенциальная энергия системы считается равной нулю.
Потенциальной энергией механической системы называется величина,
равная работе, которую совершают все действующие на систему
потенциальные силы, при переводе системы из данного состояния в нулевое.
dA= Fdr = Fx dx + Fy dy + Fz dz ; dA = - dWп ;
dWп = дWп*dx / дх + дWп*dy / дy + дWп*dz / дz
dA = Fdr = Fxdx + Fydy + Fzdz = - дWп*dx / дх - дWп*dy / дy - дWп*dz / дz
F = i * Fx + j * Fy + k * Fz = - (i *дWп / дх + j *дWп / дy + k *дWп / дz) =
= - gradWп
Потенциальная энергия матерьяльной точки в однородном поле.
Силовое поле однородно, если сила F одинакова во всех точках поля.
Рассмотрим однородный случай! Пусть сила F, приложенная к матерьяльной
точке действует вдоль оси Z ; dWп = - dA = Fz dz ;
Wп = (интеграл z0 – z1) Fz dz = - Fz (z1 – z0) = -Fz * z ; Например тело в поле
силы тяжести: F= mg ; z = h ; Wп = mgh
Теорема о кинетической энергии.
Действие результирующей силы на тело и совершаемая при
этом работа равна K (изменение кинетической энергии)
2
1
2
1
2
1
cos drFFdrFdrA
ср
dt
d
mmaF
; dr=υdt
2
1
2
1
dmdt
dt
d
mA
=
22
2
1
2
2
mm
Закон сохранения механической энергии.
Работа совершается каждый раз, когда энергия одного тела передается
другому или преобразовывается из одного вида в другой. Согласно теореме о
кинетической энергии, работа результирующих сил приводит к изменению
кинетической энергии:
А=K
2
+K
1
= K
Все силы можно разделить на 3 группы:
1) Внешние
2) Неконсервативные
3) Консервативные
Тогда А
ВН
+A
Н.К
+A
К
=K
Учитывая, что работа консервативных сил может быть выражена через
изменение потенциальной энергии, получаем соотношение:
А
ВН
+A
Н.К
=K+U=E – полная энергия
Таким образом видно, что если система тел замкнута (A
ВН
=0) и отсутствуют
неконсервативные силы (A
Н.К
=0), то E
ПОЛН
=const, K+U=const; K
1
+ U
1
= K
2
+
U
2
;
2) Основное уравнение кинетической теории газов.
Идеальным газом называют газ, в котором отсутствуют
взаимодействие между молекулами и размеры атомов пренебрежимо малы
(материальные точки), атомы или молекулы совершают упругие соударения со
стенками сосуда. При этих условиях молекулы идеального газа оказывают
силовое воздействие на стенки сосуда, которое характеризуется физической
величиной называемой давлением. P=F/S, Па. Давление – сила, действующая
на единицу поверхности.
Основное уравнение МКТ.
tSnN
fNF
t
m
f
2
2
4
2
2
2
2
2
0
0
2
0
0
0
0
0
m
nP
nm
S
Smn
S
F
P
Smn
t
m
tSnF
Поскольку молекулы движутся хаотически, то на каждую
стенку давление будет оказываться в 6 раз меньше.
2. Средняя квадратичная скорость.
kT
m
KB
2
3
2
2
0
Введенная ранее средняя
квадратичная скорость характеризует среднюю интенсивность движения,
ясно, что при хаотическом движении молекулы движутся с различными
скоростями. Очевидно, что число молекул с очень маленькими скоростями,
как и число молекул со скоростями сравнительно невелико. Основное
количество молекул имеет скорости близкие к
КВ
.
Воспользовавшись функцией распределения можно найти и среднюю
скорость молекулы. По определению среднего:
31
1)Кинематические характеристики вращательного движения.
Вращательное - движение, когда все точки тела движутся по концентрическим
окружностям, центры которых лежат на одной прямой, которая называется осью
вращения.
ω - угловая скорость, характеризующая быстроту углового перемещен
t
– средняя скорость
dt
d
– мгновенная скорость
2
2
T
- равномерное угловое вращение;
[ω] = Рад/сек.
R
L
RL
t
R
t
R
R
– линейная скорость вращения
- угловое ускорение, характеризует быстроту изменения угловой скорости.
t
;
dt
d
Скорость показывает простоту изменения тела в пространстве.
Пусть моменту времени t1 соответствует радиус-вектор r1 движущейся точки, а
близкому моменту времени t2 – радиус-вектор r2. Тогда за малый промежуток
времени (delta) t точка совершит малое перемещение, равное (delta) s = (delta) r = r2 -
r1. (рисунок – веторы r1, r2 выходят из нуля к точке 1, 2 на кривой; точки 1 и 2
соединены и образуют вектор deltaR; вектор средней скорости проходит через 1 и 2, а
просто скорость выходит из точки по прямой). v (среднее) = < v > = (delta) s / (delta) t
= (delta) r / (delta) t . Вектор средней скорости направлен вдоль вектора перемещения.
Более полно описать движение позволяет мгновенная скорость, т.е. скорость в
любой момент времени. Она равна lim (при delta t 0) delta r / delta t = r ‘ ( t ).
Вектор мгновенной скорости направлен по касательной траектории данной точки.
Модуль полной скорости равен: | v | = (корень) v (ст.2) по х + v (ст.2) по y + v (ст.2) по
z Ускорение показывает скорость изменения скорости. a ( среднее ) = delta v / delta
t. (рисунок – точка на полуокружности, от нее 2 вектора скорости, вверх и вправо, их
соединяет delta v, вдоль нее уходит в некуда вектор среднего ускорения).
Мгновенное ускорение – a = lim (delta t 0) delta v / delta t = dv / dt = v ‘ (t).
Направление вектора ускорения составляет некоторый угол с вектором скорости.
Угол АЛЬФА между векторами скорости и ускорения может изменяться в пределах 0
<= АЛЬФА <= ПИ. Углы АЛЬФА=0 и АЛЬФА=ПИ соответствуют прямолинейному
движению. При 0 <= АЛЬФА <= ПИ/2 модуль скорости возрастает, при ПИ/2 <
АЛЬФА <= ПИ модуль скорости убывает. При АЛЬФА = ПИ/2 модуль скорости не
изменяется. Вектор ускорения АЛЬФА при криволинейном движении тела обычно
представляют в виде суммы двух составляющих, направленных следующим образом:
одна по касательной к траектории – это тангенсальное ускорение, вторая по нормали
к касательной – нормальное ускорение.a (нормальное) = v (ст.2) / R //// a
(тангенсальное) = dv / dt ///// | a | = (корень) a тангенсальное (ст.2) + a нормальное
ст.2.
2) Закон распределения энергии по степеням свободы. На каждую степень
свободы приходится в среднем одинаковая кинетическая энергия, равная 1/2kT.
1. Средняя энергия одной молекулы <e >=i(kT/2). Идеальный газ – это модель,
которая во многих случаях с достаточно хорошей точностью описывает поведение
газа. Идеальный газ – это газ, молекулы которого имеют пренибрежительно малый
объем и не взаимодействуют на расстоянии. Молекулы идеального газа
взаимодействуют друг с другом только в момент соударения. Причем соударение
считается абсолютно упругим. Эти предположения (отсутствие взаимодействия,
абсолютно упругие соударения) позволяют утверждать, что внутренняя энергия
идеального газа определяется суммой кинетических энергий отдельных частиц,
причем эта кинетическая энергия не переходит ни в какие другие виды энергии.
Внутренняя энергия идеального газа состоит из учета потенциальной энергии и
кинетической энергии движения атомов или молекул, поэтому величина внутренней
энергии определяются выражением:
RT
i
U
RT
i
kT
i
N
M
m
U
N
R
kkT
i
E
Nкт
ENU
a
a
k
a
k
2
22
2
M
m
N..
Внутренняя энергия – это функция состояние газа. Она прямо пропорциональна
абсолютной температуре и характеризует энергию всех молекул газа. Внутренняя
энергия одного моля газа. Um=<e >NA=(i/2)kNAT. 3. Внутренняя энергия
произвольной массы газа. U=(m/M)UM=(m/M)(i/2)RT. Внутренняя энергия
идеального газа. U=N<e >, <e > - средняя кинетическая энергия молекул. <e >=(i/2)
(kT), где k=1,38× 10-23Дж/К, i - это сумма числа поступательных, вращательных и
колебательных степеней свободы молекул. i=iпост.+ iвращ.+2iкол..
Реальные газы. Поведение реальных газов хорошо описывается уравнением
pVM=RT только при слабых силах межмолекулярного взаимодействия. Реальный газ
- это газ, между молекулами которого существуют заметные силы межмолекулярного
взаимодействия. Для описания свойств реального газа используются уравнения,
отличающиеся от уравнения Клаперона-Менделеева. Внутренняя энергия реального
газа. U=n CvT-a'/V, где a'=n 2a. По этой формуле можно находить приближенное
значение внутренней энергии реальных газов.
32
1) N = dA / dt – мгновенная мощность.
Механическая работа и мощность.
Механическая работа – выражение, определяемое
соотношением:
A=FScos = FS
Формула может быть использована только тогда, когда F-const, a перемещение
прямолинейно. Если перемещение не прямолинейно, а F-не const, то траекторию
разбивают и считают что на S перемещение прямолинейно, а F-const
i i
ii
SFAA
2
1
dSFA
i
Примеры работы сил:
1) Работа сил упругости
2
2
0
0 00
0 00
X
kxdxkxdxkFdxA
x xx
2) Работа сил тяжести
dA=mgdh= mgdrcos=mgdh,
2
1
2
1
mghdhmgmgdhA
Работа сил тяжести не зависит от траектории, а определяется уровнем над
поверхностью земли. Силы, работа которых не зависит от траектории, а определяется
только начальным и конечным положением наз. консервативные силами (Сила
тяжести, Гравитационная, Электростатическая, ). Если F=const,
F
dt
rd
FN
-мощность.
2) Вынужденные колебания – это колебания, возникающие в колебательной системе
под влиянием переменного внешнего
воздействия.
F(t)=F
0
cosωt
2-й закон Ньютона:
t
m
F
xxx
tFxrkxxm
cos2
cos
0
2
0
0
Они происходят с частотой ω вынуждающей силы.
44222
0
0
4)(
)(
mF
A
При
22
0
2
p
, амплитуда достигает
максимального значения
На рисунке β
2
>β
1
Явление резкого возрастания амплитуды вынужденных колебаний при совпадении
частоты вынужденной силы с соответственной частотой колебаний системы называется
резонансом. Амплитуда колебаний при резонансе зависит от затухания, чем оно
больше, тем меньше амплитуда. При нулевом затуханиии амплитуда колебаний при
резонансе достигает бесконечно большой величины
При совпадении частоты внешней силы и частоты собственных колебаний тела
амплитуда вынужденных колебаний резко возрастает. Такое явление называют
механическим резонансом. Графически зависимость вынужденных колебаний от
частоты действия внешней силы показана на рисунке 10.
Явление резонанса может быть причиной разрушения машин, зданий, мостов, если
собственные их частоты совпадают с частотой периодически действующей силы.
Поэтому, например, двигатели в автомобилях устанавливают на специальных
амортизаторах, а воинским подразделениям при движении по мосту запрещается идти
«в ногу».
При отсутствии трения амплитуда вынужденных колебаний при резонансе должна
возрастать со временем неограниченно. В реальных системах амплитуда в
установившемся режиме резонанса определяется условием потерь энергии в течение
периода и работы внешней силы за то же время. Чем меньше трение, тем больше
амплитуда при резонансе.
1. Мгновенная и средняя мощность.Мощность - физическая величина,
характеризующая скорость выполнения работы. Мощность равна отношению
совершенной работы ко времени, за которое она выполнена. Мгновенная мощность -
предел, к которому стремится средняя мощность за бесконечно малый промежуток
времени. Единицей мгновенной мощности являются:
- ватт (Вт); или
- лошадиная сила (лс).
Средняя мощность -
физическая величина, равная
отношению работы к
промежутку времени за
который эта работа совершена.
В СИ средняя мощность
измеряется в ваттах.
Для характеристики
скорости, с которой совершается
работа, введена величина,
называемая мощностью. Если за промежуток времени∆tсилаF, приложенная к телу,
совершает элементарную работу ∆А, определяемую выражением
i
i
i
i
SSFAA
)(
, то мгновенная
мощность, развиваемая этой силой за время∆t есть
t
S
SF
t
A
N
cp
)(
.
Вспоминая определение мгновенной скорости(∆t→0), получим для мощности,
развиваемой силой F в данный момент времени (мгновенная мощность), следующее
определение
cosvFvFN
где угол β - угол между направлением действия силы и скоростью материальной точки.
2. Резонанс. Резонансные кривые.
A
B
A
'
B
'
t
L
R
V
F
F
1
2
h
0
mg
rd
dh
A
t
1
2
S
t
Хт— амплитуда
w — частота
внешней силы
w0 — частота
собственных
колебаний
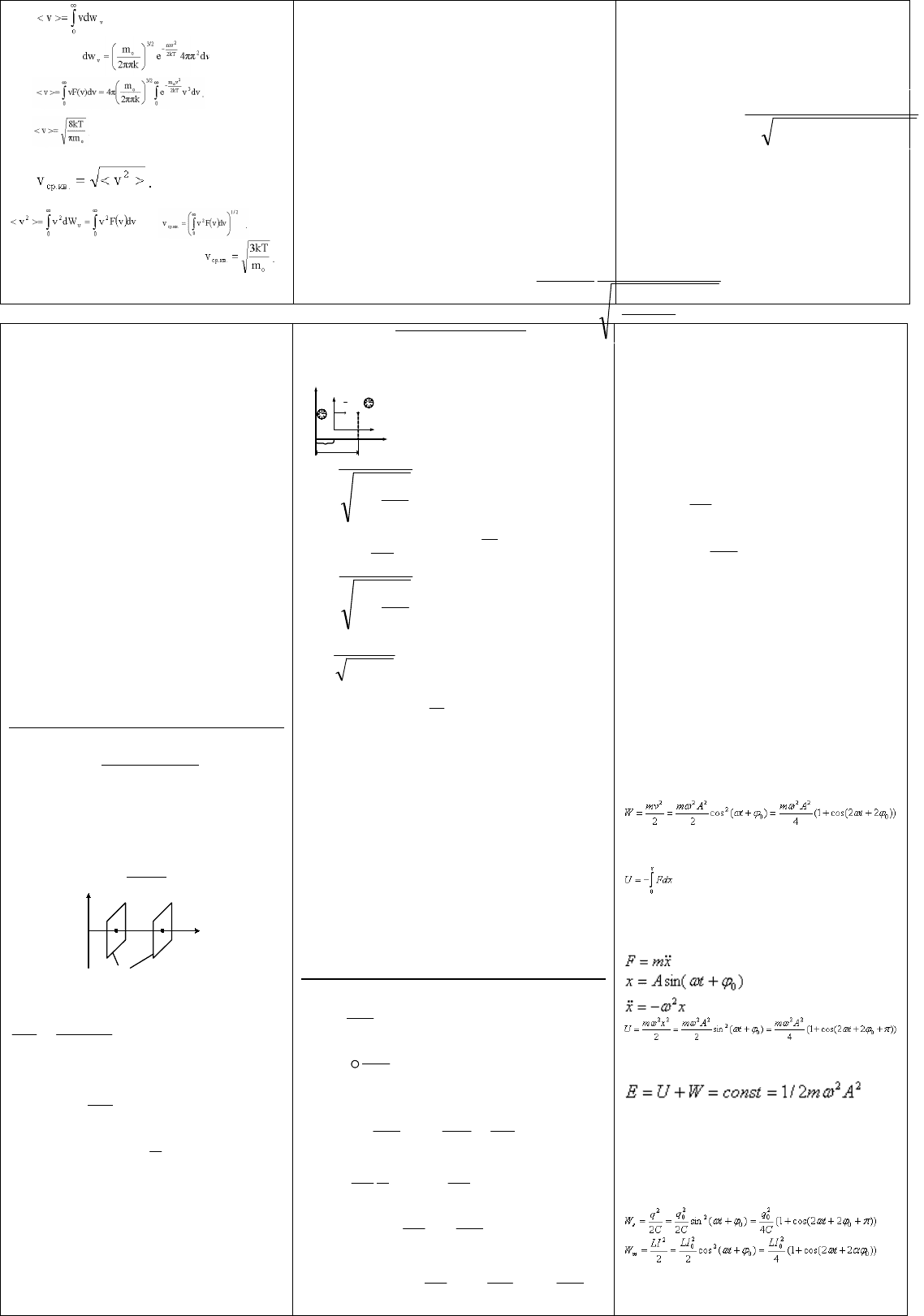
Отсюда и из получим:
Сделав замену v
2
= x и, проинтегрировав по частям, получим:
Средняя квадратичная скорость v
ср.кв.
характеризует среднюю энергию
поступательного движения молекулы. По определению:
Так как
, то:
Подставляя F(v) из (3.4) и интегрируя, получим:
Явление резкого возрастания амплитуды вынужденных колебаний при совпадении
частоты вынужденной силы с соответственной частотой колебаний системы называется
резонансом. Амплитуда колебаний при резонансе зависит от затухания, чем оно
больше, тем меньше амплитуда. При нулевом затухании амплитуда колебаний при
резонансе достигает бесконечно большой величины.
вынужденные колебания.
Амплитудно-частотные кривые-кривая,описывающая зависимость амплитуды
вынужденных установившихся колебаний от частоты внешней силы.
фазо-частотные кривые -то же для разности фаз вынужденных колебаний и внешней
силы. резонанс:
0
А=А
0
sin(
0
t+)
Ä+
0
2
A=0
2Á=(F
0
/m)sin
0
t
A=(F
0
/2m
0
)sin(t
-/2)
A
0
=F
0
/2m
0
=( F
0
/
m
0
2
)*(
0
/2)=(F
0
/k
)*Q tg = (2)/
(
0
2
-
2
)
(
0
-)/ 1
(
0
2
-
2
)
2
= (
0
-)
2
*(
0+
)
2
;
0+
≈ 2ω; 4γ
2
ω
2
≈ 4γ
2
ω
0
2
– Формула Лоренца
∆ω = 2δ=ω
0
/Q - ширина резонансной кривой.
— дектремент затухания.
(ω
0
2
-
2
)
1/2
.
График зависимости A(ω) при различных β носят название резонансных
кривых.
β
1
< β
2
< β
3
, ¶¶¶2β
2
3
> ω
2
0
, в этом случае
резонанса нет.
33 1)Вращательный момент. Моментом силы M называется величина
M=r *F
(* - скалярное произведение, все значения векторные) r – радиус-вектор, F –
сила ; r *sinАЛЬФА = l ; M = r F sinАЛЬФА = r sinАЛЬФА F = F l
(рисунок – вектор M вверх; вектор r чуть выше места, где по идее должна
быть ось OX; на 90 градусов от r от M проходит из той же точки прямая L ;
векотор F скрещивается с r под углом АЛЬФА).
Основное уравнение динамики вращательного движения. Wk = 1/2 J *
w(ст.2) ; dWk = 1/2 J 2w dw = Jwdw ; dWk = dA ; M dФИ = Jwdw;
M dФИ/dt = Jw dw/dt ; w = dФИ/dt ; E = dw/dt ; M w = J w E ; M = J E (M,E -
вектора). Основное уравнение динамики вращательного движения. Это аналог
2го закона Ньютона для вращательного движения. (F-M, m-J, a-E).
2) Рассмотрим систему, находящуюся в неравновесном состоянии. Если эту
систему изолировать от внешних воздействий. которые и вывели ее из
равновесного состояния, то через некоторое время она самопроизвольно
перейдет в равновесное состояние. Этот процес называется релаксацией.
Переход в равновесное состояние обусловлен хаотическим тепловым
движением частиц. Время, за которое первоначальное отклонение какой-лтбо
величины от ее равновесного значения уменьшается в e раз называется
временем релаксации.
Явление переноса. В термодинамической неравновесной системе возникают
особые неравновесные процессы, называемые явлением переноса., в
результате которых происходит перенос в пространстве энергии, массы и
импульса. К явлениям переноса относятся:
1) теплопроводность (перенос энергии) ; 2) диффузия (перенос массы) ;
3) внутренние трение или вязкость (перенос импульса) ;
1. Теплопроводность.
Если в некоторой области газа средняя кинетическая энергия молекул больше,
чем в остальных областях, то за счет хаотического движения молекул и
соударений между ними происходит постоянное вырабатывани кинетической
энергии молекул по всему объему газа. Энергия переносится из областей, где
температура газа выше в те области, где она ниже.
Рассмотрим одномерный случай: если T1 > T, то dQ = - æ (dT / dx) S dt ;
æ = 1/3 c p <v> <ЛЯМДА> ; c – теплоемкость, p – плотность.
Диффузия – это обусловленное тепловым движением выравнивание
концентрации смеси нескольких веществ. Этот процес наблюдается в газах,
жидкостях и твердых телах.
Рассмотрим двухкомпонентную смесь. Будем считать, что молекулы обеих
компонент обладают близкими массами и близкими значениями эффективных
диаметров. В этом случае можно считать, что <v> и <ЛЯМДА> у молекул
обеих компонент одинаковы. Эмпирическое уравнение диффузии имеет вид:
dm
i
= Д (dp
i
/ dx) dS dt.
Д – коэффициент диффузии.
Д = (1/3) <v> <ЛЯМДА> ; dpi / dx – градиент плотности ; Т.к. <v> и
<ЛЯМДА> для обеих компонент смеси примерно одинаковы, то и
коэффициент диффузии для них будет одинаков.
2) Явление переноса в газах.
Постоянное тепловое хаотическое движение приводит к непрерывному
перемещению молекул. При этом если в газе возникают какая либо
неоднородность то со временем все неоднородности выравниваются. Эти
процессы выравнивания не являются хаотическими, а характеризуются
определенной направленностью. Это связано с перемещением характеристик
газа от областей с избытком к областям с недостатком. Существует 3 типа
неоднородностей:
1)Неоднородность плотности (концентрации);
2)Неоднородность температуры (энергии);
3)Неоднородность импульса (перемещения) отдельных слоев движения газа;
Диффузия
Диффузия – процесс самопроизвольного выравнивания концентрации.
Рассмотрим перенос вещества вдоль направления оси X. Пусть
1
>
2
,
Изменение плотности вдоль X характеризуется градиентом плотности:
0
12
12
xxx
Если плотность распределяется неравномерно перенос вещества в следствии
диффузии определяется уравнением Фика:
Sdt
dx
d
Ddm
D – коэффициент диффузии
3
1
D
34 1) Преобразования Лоренца. Постулаты СТО.
Уравнения Максвелла не инвариантны относительно законов Галилея. Т.е. в разных системах отсчета
согласно преобразованиям Галилея законы электродинамики должны были бы описываться различными
уравнениями. => Либо Максвелл не прав, либо Галилей не точен.
Если вместо преобразований Галилея использовать преобразования Лоренца, то инвариантность законов
природы выполняется как для механики, так и для электродинамики.
2
2
2
2
2
1
1
'
c
V
x
c
V
t
t
c
V
Vtx
x
c
V
2
1
1
Из приведенных выражений видно, что при
0
c
V
, преобразования Лоренца переходят в
преобразования Галилея. На основе новых данных Эйнштейн построил специальную теорию
относительности в основе которой лежат 2 постулата:
1) Всеобщий принцип относительности – все законы природы одинаковы во всех инерциальных системах
отсчета.
2) Скорость света c в вакууме одинакова во всех инерциальных системах отсчета (с=3·10
8
м/с)
Постулаты специальной теории относительности. Специальная теория относительности также как и
Ньютоновская механика предполагает, что время однородно, а пространство однородно и изотопно. В
основе специальной теории относительности лежат 2 постулата, которые являются результатом
эксперементально установленных закономерностей.
1 постулат обобщает принцип механической независимости Галилея на все физические явления. В любых
инерциальных системах отсчета все физические явления при одних и тех же условиях протекают одинакова.
2 постулат выражает принцип имвариантности скорости света. Скорость света в вакууме не зависит от
скорости движения источника. Она одинакова во всех направлениях и во всех инерциальных системах
отсчета. Скорость света в вакууме является предельной скоростью в природе.
Эйнштейн пересмотрел классические свойства пространства и времени. Он предположил, что время в
различных инерциальных системах отсчета течет неодинаково. Пространство и время в теории
относительности рассматривается совместно, а не обособленно, как в Ньютоновской механике. Они
образуют единое 4х-мерное пространство и время. Возьмем в таком 4х-мерном пространстве и времени
декартовую систему координат с осями (x, y, z, ct). Положение тела в таком 4х-мерном пространстве
изображается точкой с координатами (x, y, z, ct). Эта точка называется мировой точкой. Со временем она
меняет свое положение, описывая в 4х-мерном пространстве некоторую линию, называемую мировой
линией. Даже в том случае, если тело остается неподвижным в обычном 3х-мерном пространстве, его
мировая точка перемещается вдоль оси ct.
Выберем 2 инерциальные системы отсчета k (x, y, z, t) и k’ (x’, y’, z’, t’). Будем считать, что система отсчета
k’ движется относительно системы k со скоростью v, направленной вдоль оси OX. Пусть в начальный
момент времени начала этих систем отсчета совпадают. В этот момент из начала отсчета вдоль оси OX
излучается световой импульс.
--- ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА!!!!!
Они связывают координаты и время в различных инерциальных системах отсчета. В приделе при c к
бесконечности, преобразования Лоренца переходят в преобразования Галилея. Различие в течении времени
в разных инерциальных системах отсчета обусловлено существованием предельной скорости
взаимодействий. При малых скоростях движений v0 преобразования Лоренца переходят в преобразования
Галилея.
2) Энтропия – является функцией состояния. Ее изменение связано с получением и отдачей теплоты.
Элементарное изменение энтропии при заданной температуре определяется соотношением.
T
dQ
dS
Поскольку энтропия является функцией состояния
0
dT
dQ
S
Можно показать, что любой процесс приводит к возрастанию
энтропии S>=0. Если термодинамическая система не является замкнутой т.е. имеется внешнее воздействие,
то энтропия может и убывать. Найдем изменение энтропии в процессах связанных с идеальным газом.
2
1
2
1
12
T
dA
T
dU
T
dQ
S
dTc
M
m
RdT
i
M
m
dU
V
2
V
dV
RT
M
m
pdVdA
2
1
2
1
12
V
dV
R
T
dT
c
M
m
SSS
v
35 1) Колебания – любой периодический процесс, при этом
все характеристики колебаний являются периодическими функциями.
Период – время, за которое процесс возвращается в исходное состояние.
Частота – кол-во колебаний за сек. Простейший вид колебаний –
гармонические колебания. Это колебания, происходящие по закону sin или
cos. Кинематическим уравнением гармонических колебаний является
функция:
)cos()(
0
tAtX
X – смещение частицы относительно
положения равновесия в мом. времени t.
A – амплитуда колебаний (Максимальное
смещение).
t+
0
– фаза колебаний.
0
– начальная фаза.
xtAx
dt
dV
V
tAx
dt
dx
V
2
0
2
max
0
)cos(
)sin(
Гармонические колебания – это колебания по закону sin или cos.
S(t)=A sin(wt + φ0); φ0 – фаза колебаний ; скорость v = Awcos(wt+φ0) ;
u = -Aw(ст.2) sin(wt+φ0) = - w (ст.2) A sin(wt + φ0) = - w (ст.2) S;
d2 S / dt (ст.2) = - w (ст.2) S ; d2 S / dt (ст.2) + w (ст.2) S = 0 ;
Это дифференциальное уравнение описывает гармонические колебания.
Общим решением этого уравнения является S= A1 sinwt+ A2 coswt; A2=S(0)
dS / dt = A1 w coswt + A2 w sinwt ; A1 = (1/w)(dS/dt) при t=0 ; Общее решение
можно привести к виду: S = A sin (wt + φ0), где
A = корень A1(ст.2) + A2(ст.2) ; амплитуда. φ0 = arctg (A2/A1)
Кинетическая и потенциальная энергия при механическихгармонических
колебаниях.
x = A sin (wt + φi) ; w = dx / dt = Awcos(wt + φ0) ;
Wk = mv(ст.2)/2 = 1/2 m A (ст.2) w(ст.2) cos(ст.2)(wt + φ0) ;
Wп = - (интеграл 0 - x) Fdx ; F=ma ; Wп = (интеграл 0 - x) m w (ст.2) xdx =
mw(ст.2)(интеграл 0 - x) xdx = mw(ст.2) x(ст.2) / 2 ;
Wп = (m A(ст.2) w(ст.2) / 2) sin (ст.2) (wt + φ0); W = Wк + Wп; Полная
энергия не зависит от времени! W = m A(ст.2) w(ст.2) / 2 ; Из привиденного
выражения видно, что полная энергия гармонических колебаний
пропорциональна квадрату амплитуды колебаний и также пропорциональна
квадрату частоты.
Энергия гармонических колебаний
При механических колебаниях колеблющееся тело (или материальная
точка) обладает кинетической и потенциальной энергией. Кинетическая
энергия тела W:
(Скорость тела v = ds/dt)
Для вычисления потенциальной энергии тела воспользуемся самой
общей формулой, связывающей силу и потенциальную энергию тела в поле
этой силы:
где U - потенциальная энергия, набираемая (или теряемая) телом,
движущимся в силовом поле F от точки 0 (точки, в которой потенциальная
энергия принимается равной 0) до точки х.
Для силы, линейно зависящей от смещения (как в случае наших
механических маятников, такие силы носят общее название квазиупругих
сил) мы имеем:
Сравнивая формулы
для кинетической и потенциальной энергии механического маятника, можно
сделать следующие выводы:
1. Полная механическая энергия тела не изменяется при колебаниях:
2. Частота колебаний кинетической и потенциальной энергии в 2 раза
больше частоты колебаний маятника.
3. Колебания кинетической и потенциальной энергии сдвинуты друг
относительно друга по фазе на p (на полпериода). Когда кинетическая
энергия достигает максимума, потенциальная - минимума (нуля) и наоборот.
Энергия при колебаниях постоянно перекачивается из потенциальной в
кинетическую и обратно.
В случае электрических колебаний энергия в конуре представляет собой
сумму энергии электрического поля, запасенной между обкладками
конденсатора, и энергии магнитного поля, запасенной в катушке с
индуктивностью. Вычислим обе составляющие.
Сравнивая эти формулы, можно сделать следующие выводы:
1. Полная энергия в контуре остается неизменной:
V
t
y
x
S
S
'
y'
x'
x
0
x'
0
t
'
t
p
V
0
T
x
S
x
1
x
2
1
1
2
2
0
0
0
m
F
A
2222
0
0
0
4)(
m
F
A

1
2
1
2
lnln
V
V
R
T
T
c
M
m
S
V
При
constT
1
2
ln
V
V
R
M
m
S
При
constV
1
2
ln
T
T
c
M
m
S
v
При
0dQ
0S
Энтропия системы тел равна сумме энтропий каждого из них.
Пример: Найти
S
cmdTdQ
2
1
1
2
2
1
ln
T
T
T
T
cm
T
dT
cm
T
dQ
S
T
m
T
Q
dQ
TT
dQ
S
1
- при плавлении
и испарении;
Физический смысл энтропии был раскрыт Больцманом, который связал энтропию с термодинамической
вероятностью w,
wkS ln
, где w - это число способов которыми может
быть реализовано данное состояние термодинамической системой.
Пример: спичечный коробок 1.(Спички в коробке)
Основным законом является закон возрастания энтропии. Энтропия при этом выступает
как мера упорядоченности системы. (Чем меньше энтропия тем больше порядок) Возрастание энтропии
приводит к разупорядочиванию любой системы.
Пример: спичечный коробок 2.(Коробок спичек высыпали на стол)
Следствие: все самопроизвольные процессы в природе происходят таким образом, что
энтропия возрастает. Происходят процессы от упорядочивания к беспорядку. Тем не менее возможны
процессы, когда энтропия уменьшается. Однако при этом необходимо совершить работу. Т.е. такой процесс
требует затрат энергии.
Пример: спичечный коробок 3.(Спички собрали в коробок)
Формула Больцмана
На центральном кладбище города Вены покоится прах австрийского физика Больцмана (1844-1906 гг.). На
его надгробии выгравирована формула, которая носит его имя:
S=k*ln(P), k = R/N = 1,38*10-23 Дж/К,(1)
где k - фундаментальная мировая постоянная Больцмана;
R = 8,31 Дж/(моль*К) - молярная газовая постоянная;
N = 6,06*1023 моль-1 - число Авогадро;
Р - статистический вес: число способов осуществления данного состояния.
Параметр S - энтропия - служит мерой рассеяния энергии Вселенной, а Р - характеризует любые
самопроизвольные изменения, эта величина относится к миру атомов, определяющих скрытый механизм
изменения. Итак, формула (1), вывод которой дан отдельно, связывает энтропию с хаосом.
Смысл формулы Больцмана
В условиях равновесия энтропия - функция состояния системы, которую можно измерить или вычислить
теоретически. Но стоит изолированной системе отклониться от равновесия - возникает свойство энтропии -
она только возрастает.
Представим формулу (1) в виде
P = eS/K
и обратим внимание на то, что статистический вес состояния системы P экспоненциально растет с ростом S.
Иными словами, менее упорядоченное состояние (больший хаос) имеет больший статистический вес*, т. к.
оно может быть реализовано большим числом способов. Следовательно, энтропия - мера
неупорядоченности системы.
Из-за случайных перекладываний растет беспорядок на столе, в комнате. Порядок создается искусственно,
беспорядок - самопроизвольно, т. к. ему отвечает большая вероятность, большая энтропия. Разумная
деятельность человека направлена на преодоление разупорядоченности.
Обратим внимание на то, что первое начало термодинамики (закон сохранения энергии) - закон абсолютно
строгий, это детерминированный закон. Второе начало термодинамики - закон возрастания энтропии - закон
статистический (вероятностный).
Существует даже вероятность того, что молекулы, находящиеся в кубике размером 1 см3 могут все
собраться в одной половине этого кубика. Вероятность для одной молекулы находиться в правой части
кубика: q1=1/2. При нормальных условиях в 1 см3 содержится число молекул 2,7*1019 (число Лошмидта),
тогда вероятность того, что все молекулы соберутся в правую половину кубика равна . Это исчезающе
малая величина.
Работа Больцмана - прорыв в совершенно новую область: в физику вошла вероятность, статистические
законы. Это значит, что хотя и редко, но энтропия может и убывать.
2. Частота колебаний энергий в 2 раза превосходит частоту колебаний заряда
и тока в контуре.
3. Электрическая и магнитная энергии сдвинуты по фазе на полпериода друг
относительно друга; происходит непрерывное перекачивание энергии из
одной формы в другую и обратно.
Поскольку в контуре происходят колебания электрической и магнитной
энергий, электрический колебательный контур также называют
электромагнитным.
2) Идеальный газ – это модель, которая во многих случаях с достаточно
хорошей точностью описывает поведение газа. Идеальный газ – это газ,
молекулы которого имеют пренибрежительно малый объем и не
взаимодействуют на расстоянии. Молекулы идеального газа взаимодействуют
друг с другом только в момент соударения. Причем соударение считается
абсолютно упругим. Эти предположения (отсутствие взаимодействия,
абсолютно упругие соударения) позволяют утверждать, что внутренняя
энергия идеального газа определяется суммой кинетических энергий
отдельных частиц, причем эта кинетическая энергия не переходит ни в какие
другие виды энергии. Опытным путем было установлено, что параметры
состояния газа удовлетворяют условию PV / T = const ; зависящему от
количества вещества ; PV / T = МЮ R ; (R – универсальная газовая постоянная
= 8,31 дж/моль к) ; PV = МЮ RT – уравнение Менделеева-Клайперона.
МЮ = m / μ ; 1 моль любого газа при нормальных условиях занимает ; R = k
Na ; PV = МЮ Na kT ; МЮ Na = N ; PV = NkT ; P = N k T/ V ; N0 = N/ V –
число молей в единице объема.
P = n0 k T – другая форма записи этого уравнения.
36
1) Радиус-вектором некоторой точки называется вектор, проводящийся из начала
координат в данную точку. r=xi+yj+zk. Средняя скорость движения: скалярная -
отношение пути к промежутку времени, в течение которого материальная точка
прошла этот путь Vср = L / Δt, векторная - отношение перемещения точки к
промежутку времени, в течении которого точка совершила перемещение .
Мгновенная скорость - величина, равная пределу средней векторной скорости при
уменьшении промежутка времени [м / с]
2) Явление переноса. В термодинамической неравновесной системе возникают
особые неравновесные процессы, называемые явлением переноса., в результате
которых происходит перенос в пространстве энергии, массы и импульса. К
явлениям переноса относятся:
1) теплопроводность (перенос энергии) ; 2) диффузия (перенос массы) ;
3) внутренние трение или вязкость (перенос импульса) ;
1. Теплопроводность.
Если в некоторой области газа средняя кинетическая энергия молекул больше, чем
в остальных областях, то за счет хаотического движения молекул и соударений
между ними происходит постоянное вырабатывани кинетической энергии
молекул по всему объему газа. Энергия переносится из областей, где температура
газа выше в те области, где она ниже.
Рассмотрим одномерный случай: если T1 > T, то dQ = - æ (dT / dx) S dt ;
æ = 1/3 c p <v> <ЛЯМДА> ; c – теплоемкость, p – плотность.
Явление переноса в газах.
Постоянное тепловое хаотическое движение приводит к
непрерывному перемещению молекул. При этом если в газе возникают какая либо
неоднородность то со временем все неоднородности выравниваются. Эти
процессы выравнивания не являются хаотическими, а характеризуются
определенной направленностью. Это связано с перемещением характеристик газа
от областей с избытком к областям с недостатком. Существует 3 типа
неоднородностей:
1)Неоднородность плотности (концентрации);
2)Неоднородность температуры (энергии);
3)Неоднородность импульса (перемещения) отдельных слоев
движения газа;
Вязкость или внутреннее трение. В потоке газа молекулы участвуют
одновременно в двух видах движений – хаотическом тепловом и упорядоченном
направленном движении. Пусть <v> - скорость хаотического теплового движения,
а <u> - скорость упорядоченного движения молекул ; u значительно меньше v ; В
результате движения молекул, молекулы из слоя газа, двигающегося с одной
поступательной скоростью u будут перемешиваться с молекулами из другого слоя.
В результате столкновеня молекул между собой молекулы из быстрого слоя будут
передавать часть своего импульса молекулам из медленного слоя и таким образом
тормозиться. По этой причине в газе возникает своеобразная сила внутреннего
трения, которая замедляет движение быстрых слоев и ускоряет движение
медленных слоев. Fтр = η | du / dx| S ; При увеличении температуры газа
возрастает скорость теплового движения молекул и следовательно частота
соударений между ними. Следствием этого является увеличение переноса
импульса от одного слоя газа к другому, поэтому при увеличении температуры
газа, его вязкость возрастает.
Иная картина наблюдается в жидкостях. В жидкостях основной причиной
возникновения внутреннего трения являются межмолекулярные взаимодействия
(которые в газе практически отсутствуют). С увеличением температуры жидкости
возрастает скорость теплового движения молекул и их кинетической энергии
оказывается достаточно для разрыва межмолекулярных связей. Это приводит к
ослаблению взаимодействия между молекулами и как следствие уменьшению
вязкости жидкости.
2. Вязкое трение. Коэффициент вязкого трения.
Вязкость - Явление вязкости связано с возникновением сил трения между
слоями жидкости или газа, которые перемещаются параллельно друг другу, но с
37 1) Реактивное движениею Уравнение Мещерского.
(рисунок – летящая ракета, подписи – t+dt ; m –dm ; v+dv ; над хвостом подпись – dm
(u+v)). dP = (m – dm)(v dv) + (u + v)dm – mv = mv +vdm + mdv – dm dv + udm + vdm –
mv = mdv + udm. dP = mdv + udm ; Разделим обе части на dt: dP / dt = mdv / dt + udm /
dt ; ma = F – udm / dt ; Fp = udm / dt (реактивная сила). [m*a = F – Fp] – уравнение
Мещерского.
Если внешние силы на систему не действуют, то F=0 ; ma = - udm / dt ;
mdv / dt = - udm / dt; mdv = - udm; dv = - udm / m ;
v = - (интеграл от m 0 до m 0 – m) udm / m = - u (интеграл) dm / m =
= u*ln (m 0 /m 0 - m). Уравнение цеалковского [v = u*ln (m 0 / m0 - m)]
v – конечная скорость, u – скорость истока газа, m – масса ракеты.
1. Движение тела переменой массы.
Уравнение движения тел с переменной не содержат ничего принципиально
нового по сравнению с законами Ньютона, и являются их следствиями. Но они
представляют большой интерес в связи с ракетной техникой.
Выведем уравнение движения материальной точки с переменной массой на
примере движения ракеты. Пусть m(t)-масса пакеты в произвольный момент времени t,
а v(t)-ее скорость в тот же момент. Импульс ракеты в этот момент будет mv. Спустя dt
масса и скорость ракеты получат приращение dm и dv( dm-отрицательна). Импульс
ракеты станет (m+dm)(v+dv). Сюда надо добавить импульс движения газов,
образовавшихся за dt. Он равен dm
газ
v
газ
–масса и скорость газа, образовавшихся за dt.
Вычитая из суммарного импульса системы в момент t+dt импульс системы в момент t,
найдем приращение этой величины за dt. Это приращение равно Fdt, где F –
геометрическая сумма всех внешних сил, действующих на ракету.
(m+dm)(v+dv)+dm
газ
v
газ
-mv = Fdt
Время dt устремим к нулю. Поэтому, раскрывая скобки, отбрасываем dmdv.
Далее dm+dm
газ
=0 и v
отн
=v
газ
-v есть скорость истечения газов относительно ракеты.
Тогда
mdv = v
отн
dm + Fdt , деля на dt
m(dv/dt) =v
отн
(dm/dt) + F
Член v
отн
(dm/dt) – реактивная сила . Уравнение (1)-уравнение Мещерского или
уравнение движения точки с переменной массой.
Пусть теперь у нас F=0, тогда mdv = v
отн
dm.
Допустим, что ракета движется прямолинейно в направлении,
противоположном скорости v
отн
. Тогда проекция v
отн
на направление движения будет –
v
отн
. Тогда
dv/dm = -(v
отн
/m)
Пусть скорость газовой струи v
отн
постоянна, тогда
v= - v
отн
(dm/m) = - v
отн
ln(m) + C
Значение С определяется начальными условиями. Если, в начальный момент
времени скорость ракеты =0, а масса = m
0,
тогда 0 = - v
отн
ln(m
0
) + C , откуда С = v
отн
ln(m
0
). Следовательно : v = v
отн
ln(m/m
0
) или
m
0
/m=e
v / v отн
.
Уравнение (2) – формула Циолковского. Она справедлива для нерелятивистских
движений (v и v
отн
<< c )
Релятивистская формула имеет вид :
, где = v/c .
2. Классическая теория теплоемкости. Недостатки этой теории.
38 1) Закон сохранения импульса: Если равнодействующая всех сил,
приложенных к замкнутой системе матерьяльных точек равна нулю, то
суммарный импульс в замкнутой системе остается постоянным.
Закон сохранения импульса является одним из фундаментальных законов
физики. Он справедлив не только в классической механике, но и в квантовой.
Закон сохранения импульса является следствием определенного свойства
симметрии пространства – его однородность. При параллельном переносе в
пространство замкнутой системы как целого, ее физические свойства и законы
движения не изменяются. Импульс системы матерьяльных точек может быть
выражен через импульс центромасс этой системы.
(рисунок – ось ОХ, точки 0, x1, x0, x2; от x1 и x2 вниз идут вектора – m1, m2 -
масса; расстояние от x1 до x0 = Xc – X1; от x0 до x2 = X2 – Xc)
m1 g (Xc – X1) = m2 g (X2 – Xc); m1 Xc – m1 X1 = m2 X2 – m2 Xc;
(m1 + m2) Xc = m1 X1 + m2 X2; Xc = (m1 X1 + m2 X2) / m; m= m1 + m2;
Xc= (сумма Mi Xi) / m ; r центромасс = (сумма m * r) / m ;
v центромасс = dr / dt = (d / dt)*([сумма m*v] / m) = (сумма m * dv / dt) / m =
(сумма m*v) / m = P / m ; P = m * v центромасс ; Видно, что сумма импульсов
замкнутой системы матерьяльных точек равен импульсу центромасс этой
системы – dP / dt = F1 +…+Fm ;
m * (dv центромасс / dt) = F1+…+Fm
dP / dt = F ; dP = F * dt. Произведение силы на время ее действия называется
импульсом силы.
Закон сохранения импульса.
constP
i
i
Пусть система состоит из 2-х тел. Согласно 3-у закону Ньютона
F
1
= -F
2
– равны и противоположны по направлению. Согласно 1-у закону
Ньютона действие силы приводит к изменению импульса.
dt
dP
F
1
1
dt
dP
F
2
1
0
21
dt
dP
dt
dP
P
1+
P
2
= P
1
`+ P
2
` = const.
Движение системы тел может быть охарактеризовано понятием центром масс.
Центром масс любой системы тел называется вектор, который определяются
соотношением:
OTH
vc
m
m
2/
0
1
1

разными скоростями
S
dy
d
F
Вязкость или внутреннее трение. В потоке газа молекулы участвуют
одновременно в двух видах движений – хаотическом тепловом и упорядоченном
направленном движении. Пусть <v> - скорость хаотического теплового движения,
а <u> - скорость упорядоченного движения молекул ; u значительно меньше v ; В
результате движения молекул, молекулы из слоя газа, двигающегося с одной
поступательной скоростью u будут перемешиваться с молекулами из другого слоя.
В результате столкновеня молекул между собой молекулы из быстрого слоя будут
передавать часть своего импульса молекулам из медленного слоя и таким образом
тормозиться. По этой причине в газе возникает своеобразная сила внутреннего
трения, которая замедляет движение быстрых слоев и ускоряет движение
медленных слоев.
Силы вязкого трения. Ньютон установил опытным путем, что при
скольжении друг относительно друга двух параллельных плоскостей,
пространство между которыми заполнено жидкостью, силы вязкого трения
препятствуют этому скольжению (рис. 4.1). Эта сила пропорциональна площади S
и изменению скорости на единицу длины в поперечном направлении h/v
(градиенту скорости в направлении, перпендикулярном движению) и зависит
также от вязкости жидкости :. F=Sv/h. h
2
<<S. Важно отметить, что частицы
жидкости, прилегающие к верхней пластине, движутся вместе с нею со скоростью
v (увлекаются пластиной). Напротив, частицы жидкости вблизи нижней
(неподвижной) пластины находятся в покое (прилипают к пластине). Представим,
что жидкость между пластинами состоит из плоских параллельных слоев,
движущихся равномерно (рис. 4.2). Нетрудно понять, что каждый вышележащий
слой увлекает за собой нижний соседний слой с силой F. В свою очередь, этот
нижний слой тормозит движение верхнего слоя с той же силой. На каждый слой
действуют сверху и снизу две равные, но противоположно направленные силы.
Скорость слоев возрастает от нижнего слоя к верхнему линейно (рис. 4.2), а силы
трения, действующие на каждый из слоев, одинаковы. Как результат, усилие
приложенное к верхней пластине, передается на нижнюю пластину.
2. Вязкое трение. Коэффициент вязкого трения.
Вязкость - Явление вязкости связано с возникновением сил трения между
слоями жидкости или газа, которые перемещаются параллельно друг другу, но с
разными скоростями
S
dy
d
F
Вязкость или внутреннее трение. В потоке газа молекулы участвуют
одновременно в двух видах движений – хаотическом тепловом и упорядоченном
направленном движении. Пусть <v> - скорость хаотического теплового движения,
а <u> - скорость упорядоченного движения молекул ; u значительно меньше v ; В
результате движения молекул, молекулы из слоя газа, двигающегося с одной
поступательной скоростью u будут перемешиваться с молекулами из другого слоя.
В результате столкновеня молекул между собой молекулы из быстрого слоя будут
передавать часть своего импульса молекулам из медленного слоя и таким образом
тормозиться. По этой причине в газе возникает своеобразная сила внутреннего
трения, которая замедляет движение быстрых слоев и ускоряет движение
медленных слоев.
Силы вязкого трения. Ньютон установил опытным путем, что при
скольжении друг относительно друга двух параллельных плоскостей,
пространство между которыми заполнено жидкостью, силы вязкого трения
препятствуют этому скольжению (рис. 4.1). Эта сила пропорциональна площади S
и изменению скорости на единицу длины в поперечном направлении h/v
(градиенту скорости в направлении, перпендикулярном движению) и зависит
также от вязкости жидкости :. F=Sv/h. h
2
<<S. Важно отметить, что частицы
жидкости, прилегающие к верхней пластине, движутся вместе с нею со скоростью
v (увлекаются пластиной). Напротив, частицы жидкости вблизи нижней
(неподвижной) пластины находятся в покое (прилипают к пластине). Представим,
что жидкость между пластинами состоит из плоских параллельных слоев,
движущихся равномерно (рис. 4.2). Нетрудно понять, что каждый вышележащий
слой увлекает за собой нижний соседний слой с силой F. В свою очередь, этот
нижний слой тормозит движение верхнего слоя с той же силой. На каждый слой
действуют сверху и снизу две равные, но противоположно направленные силы.
Скорость слоев возрастает от нижнего слоя к верхнему линейно (рис. 4.2), а силы
трения, действующие на каждый из слоев, одинаковы. Как результат, усилие
приложенное к верхней пластине, передается на нижнюю пластину.
i
i
i
ii
i
m
rm
R
i
i
i
ii
i
m
xm
X
,
i
i
i
ii
i
m
ym
Y
i
i
i
ii
i
m
zm
Z
Скорость движения центра масс:
i
ii
i
i
i
i
i
P
M
m
Mdt
rd
m
Mdt
Rd
111
i
MP
Центр массы системы тел, движущихся, как материальная точка в которой
сосредоточена вся масса системы.
Особенности:
1) F
ВНЕШН.
=0, то dP=0 P=const
2)Если dt 0, то действие внешних сил очень мало dP=0, P=const
3) F
x
=0, dP
x
=0, P
x
=const;
2) Вязкость или внутреннее трение. В потоке газа молекулы участвуют
одновременно в двух видах движений – хаотическом тепловом и
упорядоченном направленном движении. Пусть <v> - скорость хаотического
теплового движения, а <u> - скорость упорядоченного движения молекул ; u
значительно меньше v ; В результате движения молекул, молекулы из слоя
газа, двигающегося с одной поступательной скоростью u будут
перемешиваться с молекулами из другого слоя. В результате столкновеня
молекул между собой молекулы из быстрого слоя будут передавать часть
своего импульса молекулам из медленного слоя и таким образом тормозиться.
По этой причине в газе возникает своеобразная сила внутреннего трения,
которая замедляет движение быстрых слоев и ускоряет движение медленных
слоев. Fтр = η | du / dx| S ; При увеличении температуры газа возрастает
скорость теплового движения молекул и следовательно частота соударений
между ними. Следствием этого является увеличение переноса импульса от
одного слоя газа к другому, поэтому при увеличении температуры газа, его
вязкость возрастает.
Иная картина наблюдается в жидкостях. В жидкостях основной причиной
возникновения внутреннего трения являются межмолекулярные
взаимодействия (которые в газе практически отсутствуют). С увеличением
температуры жидкости возрастает скорость теплового движения молекул и их
кинетической энергии оказывается достаточно для разрыва межмолекулярных
связей. Это приводит к ослаблению взаимодействия между молекулами и как
следствие уменьшению вязкости жидкости.
. Явление переноса
Понятия о физической кинематике. Время релаксации.
Физическая кинетика – это микроскопическая теория процессов в
неравновестных системах. Физическая кинетика исходит из представления о
молекулярном строении рассматриваемой среды и силы взаимодействия
между частицами.
Физическая кинетика включает в себя кинетическую теорию газов,
основанную на следующих общих положениях классической статистичекой
физики:
1. В системе частиц выполняются законы сохранения энергии, импульса,
момента импульса, электрического заряда и числа частиц.
2. Все частицы являются “меченными”, т.е. тождественные частицы отличны
друг от друга.
3. Все физические процессы в системе протекают непрерывно в пространстве
и времени (не квантуются).
4. Каждая частица системы может иметь произвольное значение координат и
компонент скорости, независимо от других частиц.
Рассмотрим систему, находящуюся в неравновесном состоянии. Если эту
систему изолировать от внешних воздействий. которые и вывели ее из
равновесного состояния, то через некоторое время она самопроизвольно
перейдет в равновесное состояние. Этот процес называется релаксацией.
Переход в равновесное состояние обусловлен хаотическим тепловым
движением частиц. Время, за которое первоначальное отклонение какой-лтбо
величины от ее равновесного значения уменьшается в e раз называется
временем релаксации.
39 1) Момент силы. Моментом силы F относительно некоторой точки O
называется векторная величина M, M=[rF];|rF|=|r||F|Sina ,r-радиус-вектор
M=Fl;l=rSina , l-плечо силы
Момент импульса тела относительно неподвижной оси. Для однородного
тела, симметричного относительно оси вращения, момент импульса,
относительно точки O, лежащей на оси вращения совпадает по
направлению с вектором a . В этом случае модуль импульса относительно
оси равен M=Iw .
Закон сохранения момента импульса. Этот закон основывается на
динамики вращательного движения тела. D/dt(Iw )=MÞ dL/dt=M.Если
сумма моментов сил относительно оси равна 0, то момент импульса
данной оси остаётся постоянным. Пример скамья Жуковского.
Момент силы. 2-й закон Ньютона для вращательного движения.
Опыт показывает, что одна
и та же сила оказывает разное вращательное
действие.
],[ FRM
M=FRsinα
F
τ
=Fsinα
M=F
τ
R
Действие касательной силы на материальную точку
может привести к движению с тангенсальным ускорением:
F
=ma
a=R
F
= mR
F
R=mR
2
M=J
M=F
R
J=mR
2
- момент инерции
40 1) Потенциальная энергия.
При рассмотрении системы тел, между которыми действуют только консервативные
силы, вводят понятие потенциальная энергия. Потенциальная энергия
– fфункция,
зависящая от взаимного расположения тел. Зная ее, можно легко вычислить работу
консервативных сил, используя соотношение:
A=-(U
2
– U
1
) = U, U=U(r)= U(x;y;z) Знак ‘-’ –
показывает, что положительная работа
консервативных сил всегда приводит к
уменьшению потенциальной энергии.
A=-U
U=mg·y
A=mg·h=
=mg(y
1
-y
2
)=
=-mg(y
2
- y
1
)=
=-(U
2
-U
1
)
Протенциальная энергия может быть вычисленна с точностью до
некоторой константы.
cUU
rr
)()(
Смысл имеет только Δ.
Тело, обладающее потенциальной энергией, обладает запасом возможности совершать
работу. Конкретный вид потенциальной функции зависит от сил взаимодействия
1)
mgyU
y
2)
2
2
fx
U
x
Билет № 41
Вопрос 1
Механическая работа и мощность.
Механическая работа – выражение, определяемое
соотношением:
A=FScos = FS
Формула может быть использована только тогда, когда F-
const, a перемещение прямолинейно. Если перемещение не прямолинейно, а F-
не const, то траекторию разбивают и считают что на S перемещение
прямолинейно, а F-const
i i
ii
SFAA
2
1
dSFA
i
Примеры работы сил:
1) Работа сил упругости
2
2
0
0 00
0 00
X
kxdxkxdxkFdxA
x xx
y
x
m
1
m
2
m
3
r
1
r
2
r
3
h
y
1
y
2
mg
U
y
U
x
U
x
R
2
R
1
0
F
1
F
2
*
F
F
L
0
R
M
F
R
M
a
R
F
V
F
F
1
2
x
0
F
y
0
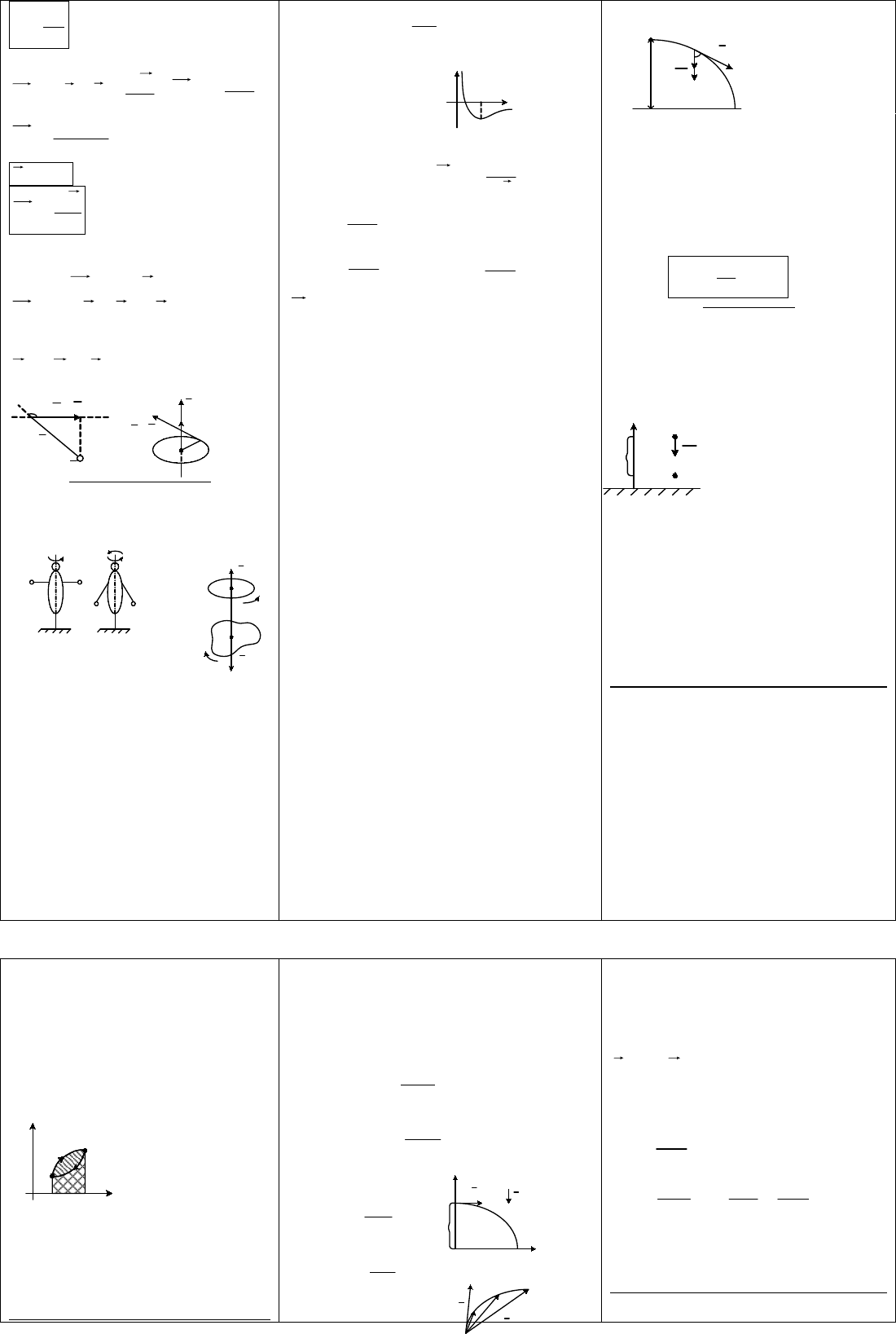
J
M
– угловое ускорение
§5.3 Момент импульса точки. 2-й закон Ньютона для вращательного
движения (в другой форме).
JM
dt
d
dt
d
JM
dt
Jd
M
)(
JL
- Момент импульса
dt
Ld
M
- в импульсной форме
Действие момента силы равно скорости изменения
момента импульса
LddtM
(Если M –const)
12
LLLtM
(при М -const)
L=J=mR
2
=mR
2
/R=mR
момент импульса и импульс точки
связаны между собой
],[
mRL
Момент импульса можно определить и относительно начала координат
L=mrsin
Закон сохранения момента импульса.
Из основного закона динамики вращательного движения
следует: если результирующий момент сил равен нулю, соответственно
dL/dt=0, то означает суммарный момент импульса остаётся постоянным.
Таким образом, если на систему не действуют ни ускорение, ни
тормозящие моменты сил, то величина и направление момента импульса
остаются постоянными.
J
1
1
= J
2
2
, если J
1
>J
2
2
>
1
L
1
=L
2
2) Эффективное сечение. Длина свободного пробега.
Молекулы газа при своем хаотическом движении сталкиваются друг с
другом, в результате этих столкновений изменяется направление
движения и модуль скорости молекул. Между двумя столкновениями
молекул проходит некоторый путь λ, который называется длинной
свободного пробега. В дальнейшем линной свободного пробега будем
называеть среднее значение < λ >.
Эффективный диаметр молекулы – минимальное расстояние, на
которое сближаются центры двух молекул в момент соударения.
Эффективный диаметр слабо зависит от температуры, уменьшаясь с ее
увеличением
< λ > = <v> t / <z> ; z – число молекул, с которыми она столнется за время
t ; Ясно, что молекула при своем движении столкнется со всеми
молекулами, центр которых находится внутри цилиндра радиусом d, а
длинна образующей <v> t.
<z> = nTd (ст.2) <v> ПИ ; < λ > = <v> t / ПИ d (ст.2) n <v> t = 1/ ПИ d (ст.2)
n
Эта формула получена нами в предположении, что движется только одна
молекула, а все остальные заморожены. Если учесть движения других
молекул, то это выражение имеет вид:
< λ > = 1 / (корень из 2) ПИ d (ст.2) n ; P = nkT ; n = P / kT;
< λ > = kT / (корень из 2) ПИ d (ст.2) P
3)
r
kQ
qgU
x
4) Атомное взаимодействие.
Выведем соотношение между консервативными силами и консервативной функцией:
dA=-dU
dUrdF
rd
dU
F
dx
dU
F
x
dy
dU
F
y
dz
dU
F
z
)(
),,( ZYX
UgradF
Потенциальная энергия. Работа, совершаемая потенциальными силами при
изменениии конфигурации системы, т.е. расположении ее частей относительно
системы отсчета не зависит от пути перехода из начального состояния в конечное. Эта
работа A1-2 определяется только начальной и конечной конфигурацией систем,
следовательно ее можно представить в виде разности значений некоторой функции
конфигурации системы, называемой потенциальной энергией Wп. A1-2= Wп (1) –
Wп (2) ;
dA= - dWп. В каждой конкретной задаче для получения однозначной энергетической
зависимости каждой потенциальной рассматриваемой системы от ее конфигурации,
выбирают нулевую конфигурацию, в которой потенциальная энергия системы
считается равной нулю.
Потенциальной энергией механической системы называется величина, равная
работе, которую совершают все действующие на систему потенциальные силы, при
переводе системы из данного состояния в нулевое. dA= Fdr = Fx dx + Fy dy + Fz dz ; dA
= - dWп ;
dWп = дWп*dx / дх + дWп*dy / дy + дWп*dz / дz
dA = Fdr = Fxdx + Fydy + Fzdz = - дWп*dx / дх - дWп*dy / дy - дWп*dz / дz
F = i * Fx + j * Fy + k * Fz = - (i *дWп / дх + j *дWп / дy + k *дWп / дz) =
= - gradWп
Потенциальная энергия матерьяльной точки в однородном поле.
Силовое поле однородно, если сила F одинакова во всех точках поля. Рассмотрим
однородный случай! Пусть сила F, приложенная к матерьяльной точке действует вдоль
оси Z ; dWп = - dA = Fz dz ;
Wп = (интеграл z0 – z1) Fz dz = - Fz (z1 – z0) = -Fz * z ; Например тело в поле силы
тяжести: F= mg ; z = h ; Wп = mgh
2) Применение 1-го начала термодинамики к изопроцессам и адиабатическому
процессу.
1) V = const изохорный => dV=0 ; d = PdV=0 ; dQ=dU ; dU = МЮ dUмол = МЮ Cv dT ;
dQ= МЮ Cv dT ; Q = (интеграл T1 – T2) МЮ Cv dT = МЮ Cv (T2 – T1) – m Cv (T2 –
T1)/ μ
2) T = const изотермический => dT= 0 ; dQ= МЮ Cv dT = 0 ; dQ = dA ;
dA = PdV ; PV = МЮ RT ; P= МЮ RT / V ; dA = МЮ RT dV / V ;
A = (интеграл V1 – V2) МЮ RTdV / V = МЮ RT (интеграл V1 – V2) dV/ V = МЮ RT
ln (V2/ V1) = МЮ RT ln (P1/ P2) ; P1 V1 = P2 V2 ;
3) P = const изобарический => dQ = PdV ; A = (интеграл V1 – V2) PdV = P (V2 – V1) ; A
= P (V2 – V1) ; dU = МЮ Cv dT ; PdV = МЮ RdT ; dQ = МЮ Cv dT + МЮ Rdt = МЮ
(Cv + R) dT ; Q = МЮ Cp (T2 – T1) ;
4) Q = const Адиабатный dA = dU ; dA = МЮ Cv dT ; PdV = - МЮ Cv dT ; PV = МЮ
RT – продифференцированное уравнение Менделеева-Клайперона ; PdV + VdP = МЮ
R dT ; … ; lnP = - γ lnP + const ; γ – коэффициент Пуассона ; lnP + lnV (ст. γ) = const ;
PV (ст. γ) = const ; (график такой же как и изотермический, только чуть выше вверх).
dA = - dU = - МЮ Cv dT ; A = - (интеграл T1 – T2) МЮ Cv dT = МЮ Cv (T1 – T2) ;
2) Работа сил тяжести
dA=mgdh=
mgdrcos=mgdh,
2
1
2
1
mghdhmgmgdhA
Работа сил тяжести не зависит от траектории,
а определяется уровнем над поверхностью земли. Силы,
работа которых не зависит от траектории, а определяется
только начальным и конечным положением наз.
консервативные силами (Сила тяжести, Гравитационная,
Электростатическая, ). Если F=const,
F
dt
rd
FN
-мощность.
Потенциальная энергия.
При рассмотрении системы тел, между которыми действуют
только консервативные силы, вводят понятие потенциальная энергия.
Потенциальная энергия
– fфункция, зависящая от взаимного расположения
тел. Зная ее, можно легко вычислить работу консервативных сил, используя
соотношение:
A=-(U
2
– U
1
) = U, U=U(r)= U(x;y;z) Знак ‘-’ – показывает, что положительная
работа консервативных сил всегда приводит к уменьшению потенциальной
энергии.
A=-U
U=mg·y
A=mg·h=
=mg(y
1
-y
2
)=
=-mg(y
2
- y
1
)=
=-(U
2
-U
1
)
Вопрос 2.
Явление переноса. В термодинамической
неравновесной системе возникают особые
неравновесные процессы, называемые явлением переноса., в результате
которых происходит перенос в пространстве энергии, массы и импульса. К
явлениям переноса относятся:
1) теплопроводность (перенос энергии) ; 2) диффузия (перенос массы) ;
3) внутренние трение или вязкость (перенос импульса) ;
1. Теплопроводность.
Если в некоторой области газа средняя кинетическая энергия молекул больше,
чем в остальных областях, то за счет хаотического движения молекул и
соударений между ними происходит постоянное вырабатывани кинетической
энергии молекул по всему объему газа. Энергия переносится из областей, где
температура газа выше в те области, где она ниже.
Рассмотрим одномерный случай: если T1 > T, то dQ = - æ (dT / dx) S dt ;
æ = 1/3 c p <v> <ЛЯМДА> ; c – теплоемкость, p – плотность.
Билет № 42
Вопрос 1 .
Кинетическая энергия – это энергия механического движения.
Изменение кинетической энергии происходит за счет работы внешних
сил.
dVk = dA = Fdr ; dr = vdt ; dWk = Fdr = F v dt = vdP
F = dP / dt = 1/m * vdP = d(P[ст.2] / 2m) ; dWk = d(P[ст.2] / 2m) ;
Wk = P[ст.2] / 2m = mv(ст.2) / 2
Связь между кинетическими энергиями в различных системах
отсчета.
(рисунок – точка, 2 системы координат k и k’, проведены 2 радиус-вектора
от начала отсчета – r и r ’) r итое = r нулевое + r итое ' ;
v итое = dv / dt = (dr нулевое / dt) + (dr итое штрих / dt) = v нулевой + v
итое’
v итое = v нулевое + v итое' ; v итое в кв. = v нулевое в кв. +2 v нулевое v
итое’ + v итое’ в кв. Wk = сумма mi vi в кв. / 2 = v нулевое в кв. *
сумма[mi /2] + 2 v нулевое *
сумма[mi vi / 2] + 1/2 *сумма[mi
vi’ в кв.] – кин. энергия.
Если выбрать начальную систему
отсчета k’ в центре масс, то vc’=0
и среднее слагаемое в
кинетической энергии равно 0.
Теорема Кёнита – Wk = Wk’ +
mvo2/2
Кинетическая энергия
механической системы равна
сумме кинетических энергий этой
системы, ее движение относительно центромасс и кинетической энергии,
которая имела бы рассматриваемая система, двигаясь поступательно со
скоростью ее центромасс.
Вопрос 2
43 1) При движении материальная точка описывает некоторую линию, т. о.
положению точки и соответствует радиус-вектор, который и является функцией
времени. Уравнение движения – функция, дающая возможность определить
положение точки в любой момент времени.
)(
)(
tfy
tfx
y
x
r = x
(t)
i + y
(t)
j + z
(t)
k;
Уравнения движения:
1)
a
=const
2
2
0
0
ta
txx
x
x
2
2
00
ta
tyy
y
н
2) x(t)=Acos(ωt + φ);
2
2
0
at
tS
Траектория (путь), Перемещение(Вектор)
t
r
мгн
Билет №44
Вопрос 1
Импульс тела – количество движения. P = m v (вектор) – справедливо для
матерьяльной точки. Если тело имеет конечный размер, то импульс этого тела
можно найти как векторную сумму импульсов матерьяльных точек, на которое
можно разбить это тело. P – импульс.
Моментом импульса (моментом количества движения) матерьяльной точки
относительно оси называется векторная величина L = r * P ; где все величины
– векторы ; r – расстояние от оси вращения до этой точки.
constP
i
i
Пусть система состоит из 2-х тел. Согласно 3-у закону Ньютона
F
1
= -F
2
– равны и противоположны по направлению. Согласно 1-у закону
Ньютона действие силы приводит к изменению импульса.
dt
dP
F
1
1
dt
dP
F
2
1
0
21
dt
dP
dt
dP
P
1+
P
2
= P
1
`+ P
2
` = const.
Движение системы тел может быть охарактеризовано понятием центром масс.
Центром масс любой системы тел называется вектор, который определяются
соотношением:
U
r
r
U
J
1
J
2
L
1
L
2
L
R
p=m
V
x
L
r
p=m
V
0
h
0
mg
rd
dh
h
y
1
y
2
mg
V
0
P
1
2
a
b
y
x
V
0
g
h
(
t
r,
)
r

Термодинамический процесс – это переход термодинамической системы
из одного состояния в другое. Термодинамический процесс называется
обратимым, если после него можно возвратить систему в исходное
состояние, при этом в исходное состояние должны вернуться и все тела,
взаимодействующие с системой. Процесс, который не удовлетворяет этим
условиям называется необратимым. Необходимым условием обратимого
процесса является его равновестность, однако не всякий равновестный
процесс обратим.
Круговым процессом или циклом называется такой в результате
которого
термодинамическая система возвращается в исходное сост. Из рисунка
видно что работа
2
1
0
V
V
a
pdVA
0
1
2
V
V
b
pdVA
baba
AAAAA
ba
AA
- прямой цикл;
ba
AA
- обратный цикл
0U
AQ
Важное значение круговых процессах является то, что система
возвращается в исходное состояние, Следовательно U=0, Q=A т.е.
Работа совершается за счет подводимой теплоты.
Второй закон термодинамики. Количество теплоты, полученное от
нагревателя, не может быть целиком преобразовано в механическую
работу циклически действующей тепловой машиной. Это и есть 2ой
закон: в циклически действующей тепловой машине невозможен
процесс, единственным результатом которого было бы
преобразование в механическую работу всего количества теплоты,
полученного от источника энергии – нагревателя. (by Кельвин
Copyright 1851). Второй закон связан с необратимостью процессов в
природе. Возможна другая формулировка: невозможен процесс,
единственным результатом которого была бы передача энергии
путем теплообмена от холодного тела к горячему. Второй закон имеет
вероятный характер. В отличие от закона сохранения энергии, второй
закон применим лишь к системам, состоящим из очень большого числа
частиц. Для таких систем необратимость процессов объясняется тем, что
обратный переход должен был бы привести систему в состояние
ничтожно малой вероятностью, практически не отличимой от
невозможности.
t
x
x
t
y
y
мгн
– всегда касательная к траектории.
t
S
ср
dt
dS
мгн
Ускорение – характеризует быстроту изменения скорости.
t
a
Полное ускорение разделяют на 2-е составляющие:
1)Тангенсальную (касательную) – характеризует изменение скорости по величине.
2)Нормальную – характеризует изменение скорости по направлению
R
a
н
2
dt
d
a
22
нполное
aaa
2) Распределения Максвелла молекул по скоростям.
kT
m
KB
2
3
2
2
0
Введенная ранее средняя квадратичная скорость характеризует
среднюю интенсивность движения, ясно, что при хаотическом движении молекулы
движутся с различными скоростями. Очевидно, что число молекул с очень
маленькими скоростями, как и число молекул со скоростями сравнительно невелико.
Основное количество молекул имеет скорости близкие к
КВ
Распределение по
скоростям установил Максвелл. Для этого он ввел функцию распределения f
().
Физический смысл этой функции заключается в том, что она позволяет вычислить
число молекул dN движущихся со скоростями в интервале (,+d) dN = f
()d
В конечном интервале (1,2):
dfN )(
2
1
12
Графическая зависимость функции распределения от скорости имеет
вид:
Аналитический вид:
T
m
T
e
T
m
Nf
2
2
2
3
0
2
)
2
(4)(
(N–общее
число молекул) (m
0
– масса одной молекулы)
RT
m
T 22
0
-
наиболее вероятная скорость
RT
m
T 88
0
-
средняя арифметическая скорость
0
33
m
kTRT
- средняя квадратичная скорость.
При увеличении температуры интенсивность движения возрастает
i
i
i
ii
i
m
rm
R
i
i
i
ii
i
m
xm
X
,
i
i
i
ii
i
m
ym
Y
i
i
i
ii
i
m
zm
Z
Скорость движения центра масс:
i
ii
i
i
i
i
i
P
M
m
Mdt
rd
m
Mdt
Rd
111
i
MP
Центр массы системы тел, движущихся, как материальная точка в которой
сосредоточена вся масса системы.
Особенности:
1) F
ВНЕШН.
=0, то dP=0 P=const
2)Если dt 0, то действие внешних сил очень мало dP=0, P=const
3) F
x
=0, dP
x
=0, P
x
=const;
Вопрос 2
Молекулы газа при своем хаотическом движении сталкиваются друг с другом,
в результате этих столкновений изменяется направление движения и модуль
скорости молекул. Между двумя столкновениями молекул проходит
некоторый путь λ, который называется длинной свободного пробега. В
дальнейшем линной свободного пробега будем называеть среднее значение <
λ >.
Эффективный диаметр молекулы – минимальное расстояние, на которое
сближаются центры двух молекул в момент соударения. Эффективный
диаметр слабо зависит от температуры, уменьшаясь с ее увеличением
< λ > = <v> t / <z> ; z – число молекул, с которыми она столнется за время t ;
Ясно, что молекула при своем движении столкнется со всеми молекулами,
центр которых находится внутри цилиндра радиусом d, а длинна образующей
<v> t.
<z> = nTd (ст.2) <v> ПИ ; < λ > = <v> t / ПИ d (ст.2) n <v> t = 1/ ПИ d (ст.2) n
Эта формула получена нами в предположении, что движется только одна
молекула, а все остальные заморожены. Если учесть движения других
молекул, то это выражение имеет вид:
< λ > = 1 / (корень из 2) ПИ d (ст.2) n ; P = nkT ; n = P / kT;
< λ > = kT / (корень из 2) ПИ d (ст.2) P
r
(t)
r
(t+
t)
r
S
0
V
1
V
2
r
1
r
2
a
n
a
V
a
N
dV
N
f
в
ср
кв
T
1
t
f
T
2
y
x
m
1
m
2
m
3
r
1
r
2
r
3

Билет №45
Вопрос 1 Физический маятник – это
твердое тело, способное совершать
колебания под действием своей силы
тяжести вокруг оси, не проходящей через
центр тяжести тела. Эта ось называется
осью качания.M = - J E ; M = m g d * sinφ
(где d – расстояние от центромасс до места
крепления физического маятника) ; J E = - mgd sinφ ; E = d2 φ / dt (ст.2) ; J
* (d2 φ / dt (ст.2)) + mgd sinφ = 0 ; d2 φ / dt (ст.2) + (mgd / J) sinφ = 0 ; Это
дифференциальное уравнение, описывающее колебания физического
маятника. При малых углах уклонения можно считать, что sinφ = φ радиан
; (d2 φ / dt (ст.2)) + mgdφ / J = 0 ; Это дифференциальное уравнение
описывает гармонические колебания, частота которых равна:d2 S / dt
(ст.2) + w0 (ст.2) S = 0 ; w0 (ст.2) = mgd / J ; w0 = корень (mgd / J) ;T =
2ПИ / w0 = 2ПИ (корень J / mgd).
Вопрос 2
Термодинамический процесс – это переход термодинамической системы
из одного состояния в другое. Термодинамический процесс называется
обратимым, если после него можно возвратить систему в исходное
состояние, при этом в исходное состояние должны вернуться и все тела,
взаимодействующие с системой. Процесс, который не удовлетворяет этим
условиям называется необратимым. Необходимым условием обратимого
процесса является его равновестность, однако не всякий равновестный
процесс обратим.
Круговым процессом
или циклом называется
такой в результате
которого
термодинамическая
система возвращается в
исходное сост. Из
рисунка видно что
работа
2
1
0
V
V
a
pdVA
0
1
2
V
V
b
pdVA
baba
AAAAA
ba
AA
- прямой цикл;
ba
AA
- обратный цикл
0U
AQ
Важное значение круговых процессах является то, что система
возвращается в исходное состояние, Следовательно U=0, Q=A т.е.
Работа совершается за счет подводимой теплоты.
Вопрос 2
Второй закон термодинамики. Количество теплоты, полученное от
нагревателя, не может быть целиком преобразовано в механическую
работу циклически действующей тепловой машиной. Это и есть 2ой
закон: в циклически действующей тепловой машине невозможен
процесс, единственным результатом которого было бы
преобразование в механическую работу всего количества теплоты,
полученного от источника энергии – нагревателя. (by Кельвин
Copyright 1851). Второй закон связан с необратимостью процессов в
природе. Возможна другая формулировка: невозможен процесс,
единственным результатом которого была бы передача энергии
путем теплообмена от холодного тела к горячему. Второй закон имеет
вероятный характер. В отличие от закона сохранения энергии, второй
закон применим лишь к системам, состоящим из очень большого числа
частиц. Для таких систем необратимость процессов объясняется тем, что
обратный переход должен был бы привести систему в состояние
ничтожно малой вероятностью, практически не отличимой от
невозможности.
Билет № 46
Вопрос 1Опыт показывает, что одна и та же
сила оказывает разное вращательное действие.
],[ FRM
M=FRsinα
F
τ
=Fsinα
M=F
τ
R
Действие касательной силы на материальную точку может привести к
движению с тангенсальным ускорением:
F
=ma
a=R
F
= mR
F
R=mR
2
M=J
M=F
R
J=mR
2
- момент инерции
J
M
– угловое ускорение
§5.3 Момент импульса точки.
2-й закон Ньютона для вращательного движения (в другой форме).
JM
dt
d
dt
d
JM
dt
Jd
M
)(
JL
- Момент импульса
dt
Ld
M
- в импульсной
форме
Действие момента силы равно скорости изменения момента импульса
LddtM
(Если M –const)
12
LLLtM
(при М -const)
L=J=mR
2
=mR
2
/R=mR
момент импульса и импульс точки связаны между
собой
],[
mRL
Момент импульса можно определить и относительно начала координат
L=mrsin
Динамика вращательного движения твёрдого тела.
Абсолютно твёрдым телом называют совокупность материальных
точек, жестко связанных между собой.
2-й з-н Ньютона вращательного движения для каждой точки
1
1
JM
2
2
JM
i
i
JM
i i
i
i
JM
i
i
MM
- результирующий момент всех сил.
i i
ii
i
ii
rmJJ
2
i
ii
rmJ
2
- момент инерции твёрдого тела.
Момент инерции характеризует меру инертности тела при
вращательном движении. Его величина зависит от массы тела, а также от
распределения массы относительно оси вращения
каждое тело может иметь
бесчисленное количество моментов инерции определяемых относительно разных осей
вращения.
Таким образом, получили основной закон динамики вращательного движения:
J
M
i
i
LL
Вопрос 2
Уравнение состояния идеального газа. Параметры состояния связаны друг с другом.
Уравнение состояния устанавливает связь между параметрами состояния. В
простейшем случае состояние термодинамической системы описывается тремя
параметрами – P, V, T.
F (P, V, T) = 0 ; Идеальный газ – это модель, которая во многих случаях с достаточно
хорошей точностью описывает поведение газа. Идеальный газ – это газ, молекулы
которого имеют пренибрежительно малый объем и не взаимодействуют на расстоянии.
Молекулы идеального газа взаимодействуют друг с другом только в момент
соударения. Причем соударение считается абсолютно упругим. Эти предположения
(отсутствие взаимодействия, абсолютно упругие соударения) позволяют утверждать,
что внутренняя энергия идеального газа определяется суммой кинетических энергий
отдельных частиц, причем эта кинетическая энергия не переходит ни в какие другие
виды энергии. Опытным путем было установлено, что параметры состояния газа
удовлетворяют условию PV / T = const ; зависящему от количества вещества ; PV / T =
МЮ R ; (R – универсальная газовая постоянная = 8,31 дж/моль к) ; PV = МЮ RT –
уравнение Менделеева-Клайперона. МЮ = m / μ ; 1 моль любого газа при
нормальных условиях занимает ; R = k Na ; PV = МЮ Na kT ; МЮ Na = N ; PV = NkT ;
P = N k T/ V ; N0 = N/ V – число молей в единице объема.
47
i
ii
rmJ
2
Теорема Штейнера: Момент инерции тонкого стержня
dJ=dmx
2
=m/ L – линейная плотность
dm=dx
dJ= x
2
dx
2
0
2
0
3
1
mldxxdJJ
ll
Моменты инерции тел:
1) Материальная точка J=mR
2
2) Обруч J=mR
2
3) Диск (цилиндр) J=1/2mR
2
4) Шар J=2/5mR
2
5) Тонкий стержень J=1/12mL
2
6) Полый цилиндр J=1/2(R
1
2
+R
2
2
)
Если известен момент инерции относительно оси,
проходящей через центр инерции J
0
, то момент инерции J относительно
другой оси, параллельной первой, можно вычислить по формуле J=J
0
+ md
2
Вопрос 2
Количество теплоты сообщенное термодинамической системе
идет на изменение внутренней энергии и на совершение термодинамической
системой работы над внешними телами. Q=U+A.
Количеством теплоты Q называют энергию, которая
передается вследствие теплопередачи. Виды теплопередачи:
а)Теплопроводность – перенос энергии без
переноса вещества
б)Конвекция – перенос энергии с переносом
вещества
в)Излучение – перенос энергии посредством электромагнитного излучения
1-й закон термодинамики в различных процессах:
1)T=const, U=0, Q=A;
2)V=const, A=0, Q=U;
3)P=const, Q=U+PV;
4)Q=0, U=A
0
a
F
ц.м.
mg
V
0
P
1
2
a
b
R
2
R
1
0
F
1
F
2
*
F
F
L
0
R
M
F
R
M
a
R
F
L
R
p=m
V
x
L
r
p=mV
0
0
0'
r
i
r
j
m
i
m
j
O
O'
0
x
dx
L
R
1
R
2
d
J
0
J
ц.м.

P = n0 k T – другая форма записи этого уравнения.
Билет №48
Вопрос 1
Преобразования Лоренца. Постулаты СТО.
Уравнения Максвелла не инвариантны относительно законов Галилея.
Т.е. в разных системах отсчета согласно преобразованиям Галилея законы
электродинамики должны были бы описываться различными
уравнениями. => Либо Максвелл не прав, либо Галилей не точен.
Если вместо преобразований Галилея использовать преобразования
Лоренца, то инвариантность законов природы выполняется как для
механики, так и для электродинамики
2
2
2
2
2
1
1
'
c
V
x
c
V
t
t
c
V
Vtx
x
c
V
2
1
1
Из приведенных выражений видно, что при
0
c
V
,
преобразования Лоренца переходят в преобразования Галилея. На основе
новых данных Эйнштейн построил специальную теорию относительности
в основе которой лежат 2 постулата: 1) Всеобщий принцип
относительности – все законы природы одинаковы во всех инерциальных
системах отсчета. 2) Скорость света c в вакууме одинакова во всех
инерциальных системах отсчет
c
l
l
V
llll
ll
lxxVtxVtxxxl
Vtxx
Vtxx
xxl
2
0
0
12010212
011
022
12
1
)()()(''
)('
)('
''
а (с=3·10
8
м/с) Сокращение длинны . Пусть некоторый предмет находится в
системе S`. Наблюдатель в системе S` измеряя длину корабля получит:
Наблюдателю в системе S будет казаться, что все предметы в системе S`
сокращаются в направлении движения.Следствие: Расстояние между точками
относительно. В соответствии с принципом относительности системы S и S`
равноправны, поэтому наблюдателю находящемуся в системе S` также будет
казаться, что все предметы в системе S сжимаются => расстояние между точками
относительно.Удлинение промежутков времени.Пусть в системе S с
координатой x
0
произошло 2 события t
1
и t
2
(t
1
-включили прожектор, t
2
-
выключили). t=t
2
– t
1
Наблюдатель в системе S` измеряя этот промежуток
времени по своим часам, получит величину:
c
t
t
V
tt
t
t
t
tt
c
V
t
c
V
t
t
ttt
2
0
2
22
12
2
0
2
1
2
0
2
2
12
1
1
111
x
1
x
Наблюдателю в системе S` будет казаться, что движущиеся относительно него в
системе S процессы замедляются. Наименьшее значение имеет промежуток
времени в той системе отсчета, в которой события происходят и относительно
которой часы находятся в покое. Это время называют собственным.
Следствие: Относительность понятий одновременности. Релятивистская
динамика
Сложение скоростей.Преобразования Лоренца позволяют получить:
Билет №49
Вопрос 1
Сложение колебаний с близкими частотами. Биения.
Пусть есть 2 колебания:
x
1
=A
1
cos(ω
1
t+φ
01
)
x
2
=A
1
cos(ω
2
t+φ
02
)
ω
2
=ω
1
+Δω
Δω – очень мало
0022011)(
)(21
2
2
2
1
)()(
)cos(2
ttt
AAAAA
t
t
При сложении таких колебаний вектор A
2
будет “убегать” от вектора
A
1
, при этом cosΔφ(t) будет в [-1,1], поэтому амплитуда будет меняться в интервале
Amin=|A
1
-A
2
|
Amax=|A
1
+A
2
|
Такие колебания называются биения.
Вопрос 2
Круговые процессы являются основой всех тепловых машин. кот бывают 2-х типов
1)Реализующие прямой цикл Q=A>0, т.е. тепло мех. раб.
2)Реализующие обратный цикл Q=A<0, т.е. мех. раб.
тепло
Общая схема всех тепловых двигателей:
1
2
1
Q
Q
Q
A
Идеальная тепловая
машина Карно.
В ее основе
лежит круговой процесс
который называется циклом
Карно
1-2: A
1
=Q
1
>0 – Изотерм.
расширение
2-3: Q=0 – Адиабатическое
расширение;
3-4: A
2
=Q
2
<0 –
Изотермическое сжатие;
4-1: Q=0 Адиабатическое
сжатие.
Для
замкнутых циклов работа
совершаемая газом в цикле Карно равна подводимому теплу. Тепловая машина
реализующая этот цикл имеет максимальный КПД по сравнению с любым другим
циклом. =(T
1
-T
2
)/T
1
; Для повышения КПД тепловых машин Необходимо увеличивать
температуру нагревателя и уменьшать температуру холодильника. КПД любой
реальной тепловой всегда меньше, чем у машины Карно:
1
21
1
21
Q
QQ
T
TT
Билет №50
Вопрос 1
Динамика частиц. 1-й закон Ньютона.
Динамика – раздел механики, в котором изучаются причины возникновения или
изменения в движении тел. В основе лежат 3 закона Ньютона.
1-й закон Ньютона: Если на тело не действуют другие тела, или их действие
скомпенсировано, то тело находится в состоянии покоя или в состоянии
равномерного прямолинейного движения. Состояние покоя или состояние
равномерного прямолинейного движения – это природное свойство всех тел – это
свойство называется инертностью. Системы отсчёта, в которых выполняется 1-й
закон Ньютона, называются инерциальными системами отсчёта.
Все инерциальные системы отсчета движутся друг относительно
друга равномерно и прямолинейно. Системы отсчета, в которых тела движутся с
ускорением, называются неинерциальными.
Силы. 2-й закон Ньютона.
2-й закон Ньютона: Ускорение, которое приобретает тело прямо
пропорционально результирующей всех сил, действующих на тело и обратно
пропорционально массе.
m
F
a
,
.......
21
FFF
Силой называется векторная физическая величина, которая характеризует
действие одного тела на другое.
2
21
r
mm
GF
2
21
r
qq
kF
F=qυBsinα
Импульсная форма 2-го закона Ньютона.
dt
md
dt
d
mamF
mP
dt
Pd
F
– 2-й закон Ньютона - общая формулировка
PddtF
Действие силы в течении t приводит к изменению импульса тела. Если F-const
FΔt=ΔP
3-й закон Ньютона (Закон взаимодействия тел).
3-й закон Ньютона: два тела взаимодействуют друг с другом с
силами, равными по величине и по модулю, но противоположными по
направлению
Силы прилаженные к разным телам и никогда не могут
компенсировать друг друга
Вопрос 2
Распределение Больцмана .
Распределение Больцмана – распределение частиц в потенциальном поле.
Барометрическая формула является частным случаем распределения частиц в
потенциальном поле. Преобразуем его используя уравнение Менделеева-
Клапейрона в виде: p=nkT
kT
ghm
kTennkT
0
0
ghmW
П 0
kT
W
П
enn
0
-распределение Больцмана.
Анализ:
1)T ∞, следовательно W
П
/kT 0, n=n
0
2)T 0, след. W
П
/kT ∞, n 0, Все молекулы
падают на землю.
V
0
P
V
0
P
нагреватель
рабочее
тело
холодильник
Q
1
Q
2
=>
T
1
T
2
A=Q
1
-Q
2
V
0
P
1
2
3
4
Q
1
Q
2
mg
N
F
N
mg
mg
F
F
mg
y
=-kx
F
F
т
р
F
1
F
2
F
1
F
2
N
m
g
P

dt
dx
U
td
dx
U
x
x
'
2
1
c
VU
VU
U
x
x
x
VUU
c
V
ипр
xx
1
Вопрос 2
Удельной теплоемкостью называется количество теплоты, которое необходимо
сообщить систем, чтобы нагреть единицу массы на 1 градус:
mdT
dQ
c
– удельная теплоёмкость
Молярной теплоемкостью называют количество теплоты которое необходимо
сообщить системе, чтобы нагрет 1 моль на 1 градус
dT
dQ
c
c
c
Найдем C
идеального газа
1)
constV
dUdQ
R
i
dT
RdT
i
dT
dU
dT
dQ
c
V
2
2
2)
constp
RcRR
i
dT
RdTRdT
i
dT
pdVdU
dT
dQ
c
Vp
2
2
i
i
c
c
v
p
2
0A
UQ
