Осипов П.Ф. Гидроаэромеханика бурения и крепления скважин

Подождите немного. Документ загружается.

Часть I. Раздел 1. Уравнения гидростатики буровых жидкостей

пл

=0 р

=р

пл

p =2р

пл

p>р

пл

газ

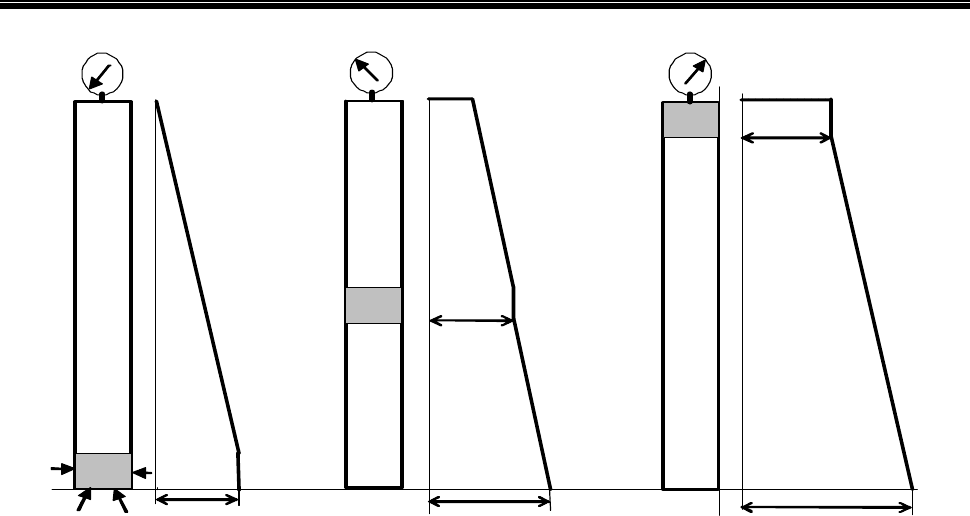
Рис. 1.7. Изменение давления в герметичной скважине при всплытии

газа, поступившего из вскрытого пласта

При анализе всплытия газового пузыря в герметично закрытой скважине мы

считали жидкость абсолютно несжимаемой. И пришли к выводу, формально

правильному, что даже совсем небольшой газовый пузырек может привести к

плачевному результату. На деле, разумеется, дело обстоит несколько иначе.

Дело в том, что эффект этот может проявиться только там, где величина объем

ной деформации жидкости под действием давления в газовом пузыре сущест-

венно меньше объема газового пузыря, всплывающего по скважине вверх. Из-

вестно, что при увеличении давления на 10 МПа объем жидкости уменьшается

на 0,5%. Предположим теперь, что из пласта с давлением 30 МПа в скважину

поступил газ с глубины 3000 м. Примем, что высота столба

газа равна 10 м.

Оказавшись на устье, газовый пузырь создает дополнительное давление на

жидкость 30 МПа. Под действием такого давления жидкость сожмется на 1,5%,

т.е. уровень жидкости в скважине (под газовым пузырем) "просядет" на 45 м,

что в 4,5 раза больше объема газа. Очевидно, что такая предоставившаяся газу

возможность расшириться приведет к уменьшению давления в

газовом пузыре

и равновесие наступит при значительно меньших давлениях по сравнению с

ожидаемыми, полученными при расчетах без учета сжимаемости жидкости.

Установлено, что описанный выше эффект роста давления до опасных вели-

чин на устье и в скважине в целом наблюдается при поступлении газа более 5%

от объема скважины, причем неважно, поступает он

сразу или постепенно.

Именно поэтому нужно быть предельно внимательным со скважинами, нахо-

дящимися под давлением или находящимися во временной консервации со

вскрытым газовым пластом.

Часть I. Раздел 1. Уравнения гидростатики буровых жидкостей

1.4. Равновесие газов в скважине

При бурении скважин на различных этапах ее строительства создаются си-

туации, когда скважина (обычно закрытая) заполнена сжатым газом, создаю-

щим определенное давление на стенки скважины. Знание величины этого дав-

ления необходимо для расчетов обсадных колонн, оценки вероятности гидро-

разрыва пласта и т.п. Поэтому умение

прогнозировать ожидаемые давления при

возможных газопроявлениях с полным или частичным замещением жидкости в

скважине газом имеет важнейшее значение.

Предположим, что закрытая скважина от кровли газоносного пласта до

устья заполнена газом (рис. 1.8). Для того чтобы этот газ находился в равнове-

сии, необходимо, чтобы столб газа создавал на пласт давление, равное давле-

нию

газа в пласте.

Воспользуемся дифференциальным уравнением гидростатики.

dp=ρ(j

dx+j

dy+j

dz),

где ρ≠const (в отличие от капельной жидкости в данном случае ρ – функция

температуры и давления).

Для поля земного тяготения j

=0; j

=-g, тогда

dp=-ρgdz.

Как отмечалось, для газа ρ=f(p,T). Для случая покоя газа в скважине можно с

некоторым допущением принять процесс сжатия изотермическим, для которого

=pV

или

отсюда

ρ=

Подставив в дифференциальное уравнение гидростатики, имеем:

pdz

−⋅⋅

Здесь р

и ρ

– известные давление и плотность в известном сечении.

Разделим переменные:

=−

Проинтегрируем:

gdz

=−

∫∫

;

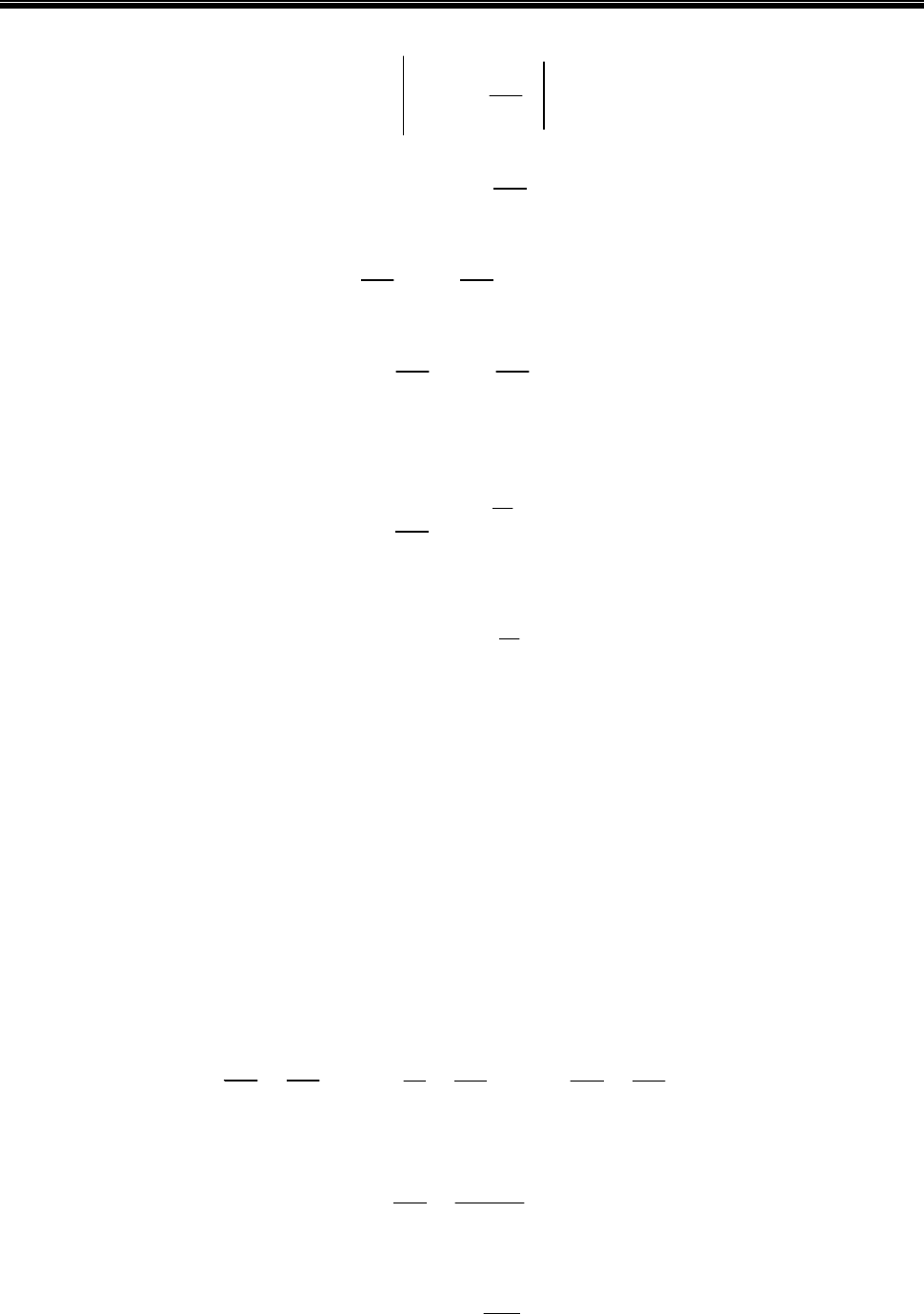
Часть I. Раздел 1. Уравнения гидростатики буровых жидкостей

=−

;

()

ln ln

pgzz

−=− −

;

()

gzz

=− −

;

=−

где h – превышение сечения z над z

(положительное или отрицательное).

Из последнего выражения следует:

−

отсюда

ppe

−

. (1.10)

Выражение (1.10) не очень удобно для расчетов, поскольку плотность ρ

, как

правило, не известна. Воспользуемся уравнением Менделеева-Клапейрона

=mR

T, (1.11)

чтобы приближенно выразить ρ

. В уравнении (1.11):

– объем одного моля газа;

– универсальная газовая постоянная, Дж/(град

кмоль);

Т – абсолютная температура, °К;

т – коэффициент сжимаемости газа, показывающий отклонение поведения

газа от идеального.

Разделив обе части уравнения на молекулярный вес газа М и заменив p/ρ на

/ρ

, получим:

;

В результате –

mR T

, (1.12)

следовательно, подставляя (1.12) в формулу (1.10):

mR T

ррe

−

. (1.13)

Часть I. Раздел 1. Уравнения гидростатики буровых жидкостей

Эта формула известна под именем барометрической.

В расчетной практике часто свойства газов описываются с помощью коэф-

фициента сжимаемости т и относительной плотности газа по воздуху в нор-

мальных условиях

Для природных газов чаще используется формула:

()

0,03415

ppe

ρ−

−

, (1.14)

где

z-z

=h.

Для практических расчетов вполне допустимо величину

0,03415

принять

равной

-4

. Тогда формула (1.14) примет вид:

()

ppe

−

−ρ − ⋅

. (1.15)

Формула (1.15) используется при расчете обсадных колонн в условиях газо-

проявлений. В известной "Инструкции по расчету обсадных колонн" она пре-

образована к виду:

()

кр y

пл

−

ρ−⋅

, (1.16)

где z

– расстояние от устья до искомого сечения.

По этой формуле можно определить давление газа на любой глубине, если

известно давление газа в пласте р

пл

В частном случае, на устье скважины при z

=0, давление равно:

кр

пл

−

ρ⋅

. (1.17)

1.5. Относительное равновесие жидкости

В буровой практике находят применение гидравлические аппараты, в кото-

рых жидкость вращается в цилиндрических сосудах, например, в гидроцикло-

нах и центрифугах.

В центрифуге (а с некоторым приближением и в гидроциклонах) жидкость

вращается с постоянной для всех частиц жидкости угловой скоростью. В по-

добных случаях говорят, что жидкость

находится в относительном равнове-

сии по отношению к стенкам вращающегося сосуда или одних частиц жидко-

сти по отношению к другим.

В названных устройствах жидкость вращается с такими угловыми скоро-

стями, что созданное этим вращением силовое поле (после центробежных сил)

оказывается более напряженным, чем поле земного тяготения, причем настоль-

ко, что

последним можно пренебречь.

Воспользуемся дифференциальным уравнением гидростатики

Часть I. Раздел 1. Уравнения гидростатики буровых жидкостей

dp=ρ(j

dx+j

dy+j

dz).

В соответствии с ранее сказанным

=0.

Центробежную силу направляем вдоль оси Ох, тогда

=0, a j

В результате получаем дифференциальное уравнение:

dp=ρw

xdx.

Интегрируем:

Постоянную интегрирования найдем, исходя из граничных условий: при

x=r

р=р

, (например, на свободной поверхности).

Тогда

;

=−

Подставив найденное С в уравнение, находим:

()

pxr

=+ −

. (1.18)

Если жидкость полностью заполняет вращающийся сосуд или сама враща-

ется в неподвижном сосуде (например, в гидроциклоне), то r

=0, то

pp=+ρ

. (1.19)

Пример. Центрифуга диаметром 400 мм. Плотность жидкости ρ=1200 кг/м

Частота вращения п=2000 мин

-1

. Определить давление на стенки корпуса цен-

трифуги, если избыточное давление в центре р

=0.

Определим угловую скорость вращения жидкости:

3,14 2000

209,4( / )

30 30

ад c

π⋅

== =

Радиус центрифуги х=0,2 м. Тогда

209,4 0,2

1200 1052360 1,052

аМПа

⋅

===

Формула (1.19) применима для определения давления на стенки скважины,

возникающего при вращении, например, алмазного долота.

Часть I. Раздел 2. Особенности гидростатики вязкопластичных жидкостей (ВЖП)

2. Особенности гидростатики вязкопластичных жидкостей (ВПЖ)

2.1. Общие замечания

Системы, обладающие тиксотропными свойствами, создающими тиксо-

тропную структуру, как ранее отмечалось, обладают свойствами твердого тела,

обладают некоторой, пусть небольшой, начальной прочностью, оцениваемой

величиной статического напряжения сдвига θ. Значение θ зависит от времени, в

течение которого вязкопластичная жидкость находилась в покое. Для разных

буровых растворов, которые часто, особенно глинистые растворы, обработан-

ные "старыми" реагентами-стабилизаторами, такими как УЩР, ТЩР, КССБ,

КМЦ и др., относятся, как указывалось выше, к реологически нестационарным

системам. Для них соотношение τ

и θ может быть самым различным. При не-

больших тиксотропных свойствах θ<τ

, а при сильно выраженной склонности

наращивать во времени прочность может быть и так, что θ>>τ

(этот случай по-

казан на рис. В.2).

Предположим, что скважина (рис. 2.1) заполнена вязкопластичной жидко-

стью, подчиняющейся модели Шведова-Бингама с реологическими показателя-

ми τ

, η и статическим напряжением сдвига (начальной прочностью) θ. Давле-

ние, создаваемое такой жидкостью на стенки скважины, в том числе и на про-

дуктивные пласты, можно определять по формулам, полученным ранее для вяз-

кой, ньютоновской, жидкости:

р=ρgL.

Предположим теперь, что скважина вскрыла пласт, давление которого р

пл

>р,

т.е. р

пл

>ρgL.

Если бы в скважине была не вязкопластич-

ная, а вязкая жидкость, то сразу бы началось

движение жидкости из скважины, т.е. нефте-,

водо- или газопроявление. Совсем другое дело,

когда в скважине вязкопластичная жидкость.

Чтобы сдвинуть ее, необходимо приложить к

ней давление, превышающее р на величину,

достаточную для преодоления сил

сопротивле-

ния, вызванных "к жизни" наличием статиче-

ского напряжения сдвига θ.

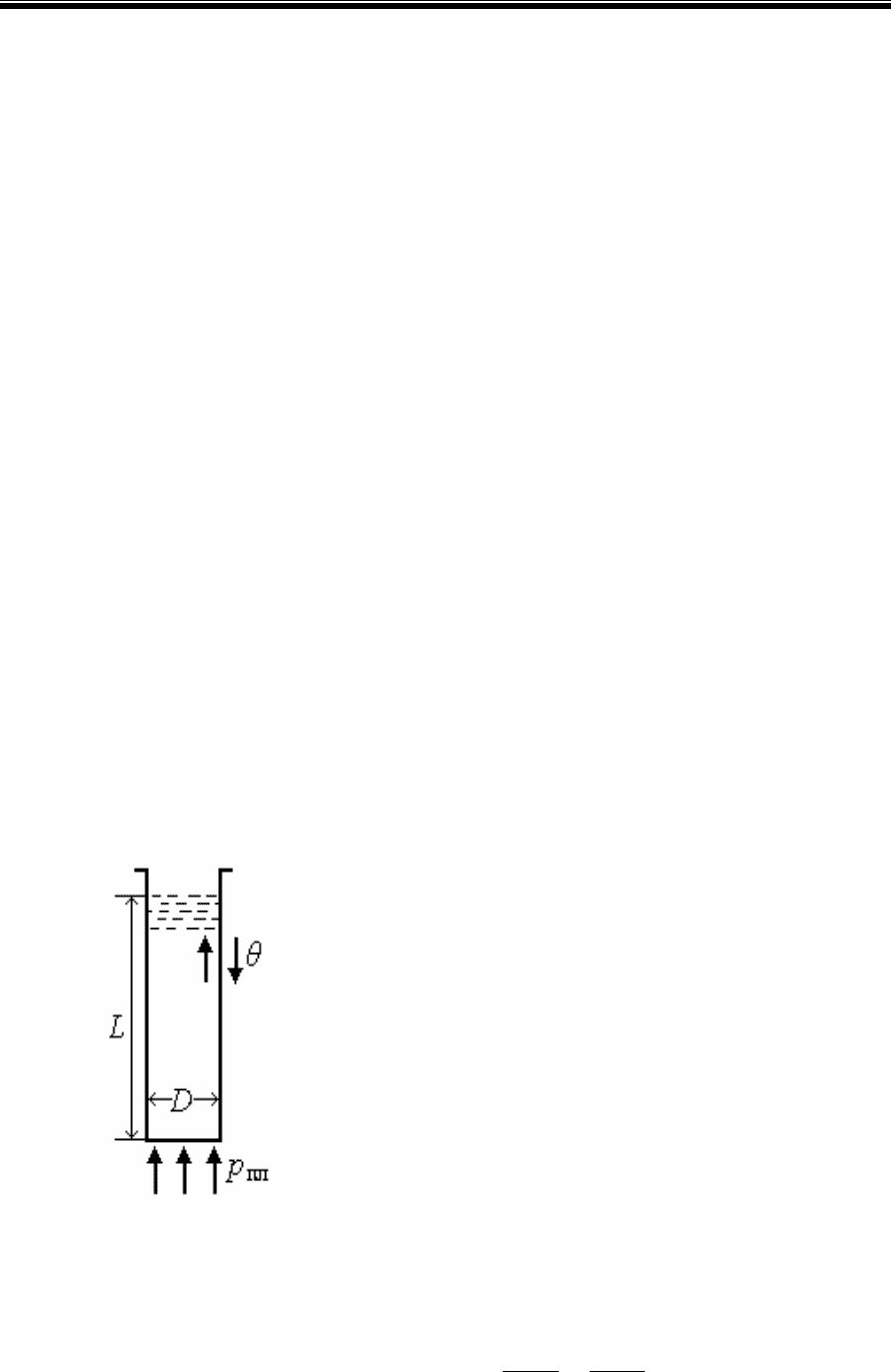
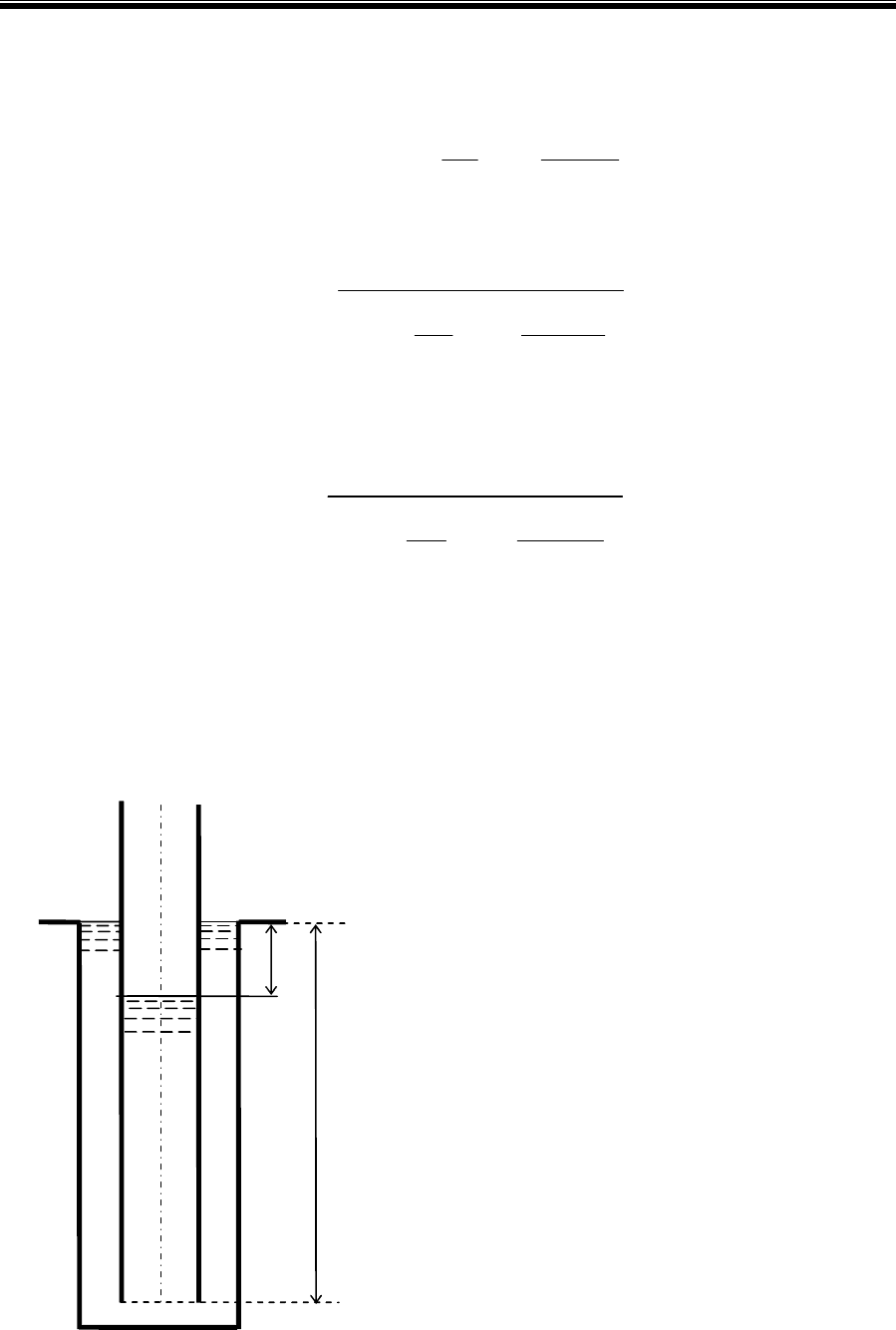
Опишем предельное состояние равновесия

между внешней силой, выталкивающей жид-

кость из скважины, диаметром D, длиной L

(рис. 2.1) и силами сопротивления, препятст-

вующими такому выталкиванию:

pgLDL

ππ

=ρ

+π θ

Рис. 2.1. Статическое рав-

новесие вязкопластичной

жидкости

Часть I. Раздел 2. Особенности гидростатики вязкопластичных жидкостей (ВЖП)

отсюда

pgL

=ρ +

. (2.1)

Следовательно, только в том случае, если р

пл

превысит на величину

(

/D) гидростатическое давление столба бурового раствора, скважина нач-

нет "проявлять".

2.2. Расчет "пусковых" давлений на насосах

Расчет сводится к решению задачи: какое давление нужно создать в спу-

щенных в скважину трубах, чтобы вывести вязкопластичную жидкость, кото-

рой заполнены трубы и скважина, из состояния покоя.

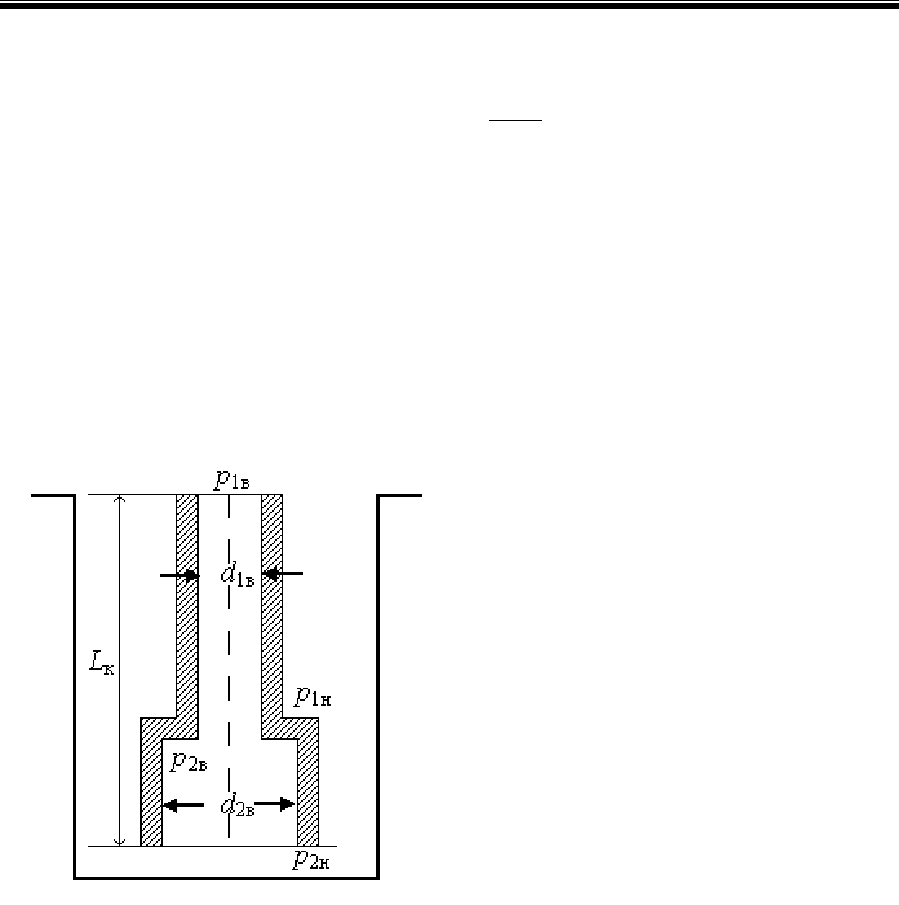
Показанная на рис. 2.2 система

труб представляет собой

систему

сообщающихся сосудов, один из

которых образован стенками сква-

жины и наружными стенками труб,

а другой – самой трубой. Примем,

что колонна труб состоит из сек-

ций труб двух размеров d

и d

Длина секции соответственно l

. Диаметр скважины – D. Длина

колонны – L

. Внутренний диаметр

труб d

1в

и d

2в

Усложним задачу. Договоримся,

что колонна труб заполнена жидко-

стью с ρ

, θ

, а заколонное – с пара-

метрами ρ

кп

, θ

кп

, причем ρ

кп

>ρ

. Та-

кая ситуация создается, например, в

конце цементирования обсадной ко-

лонны, когда в кольцевом простран-

стве за трубами находится еще не

начавший застывать цементный раствор, а в колонне – продавочная жидкость.

Условие предельного равновесия вязкпластичной жидкости в этом случае

запишется следующим образом.

−(р

1в

+р

2в

+р

1н

+р

2н

)−(ρ

кп

−ρ

)gL=0,

где р

– "пусковое" давление;

1в

и р

2в

– давления, необходимые для преодоления сил, вызванных напря-

жениями θ в трубах;

1н

и р

2н

– то же для заколонного пространства.

Рис. 2.2. Состояние статического

равновесия вязкопластичной жидкости,

когда в скважину спущена

двухсекционная колонна труб

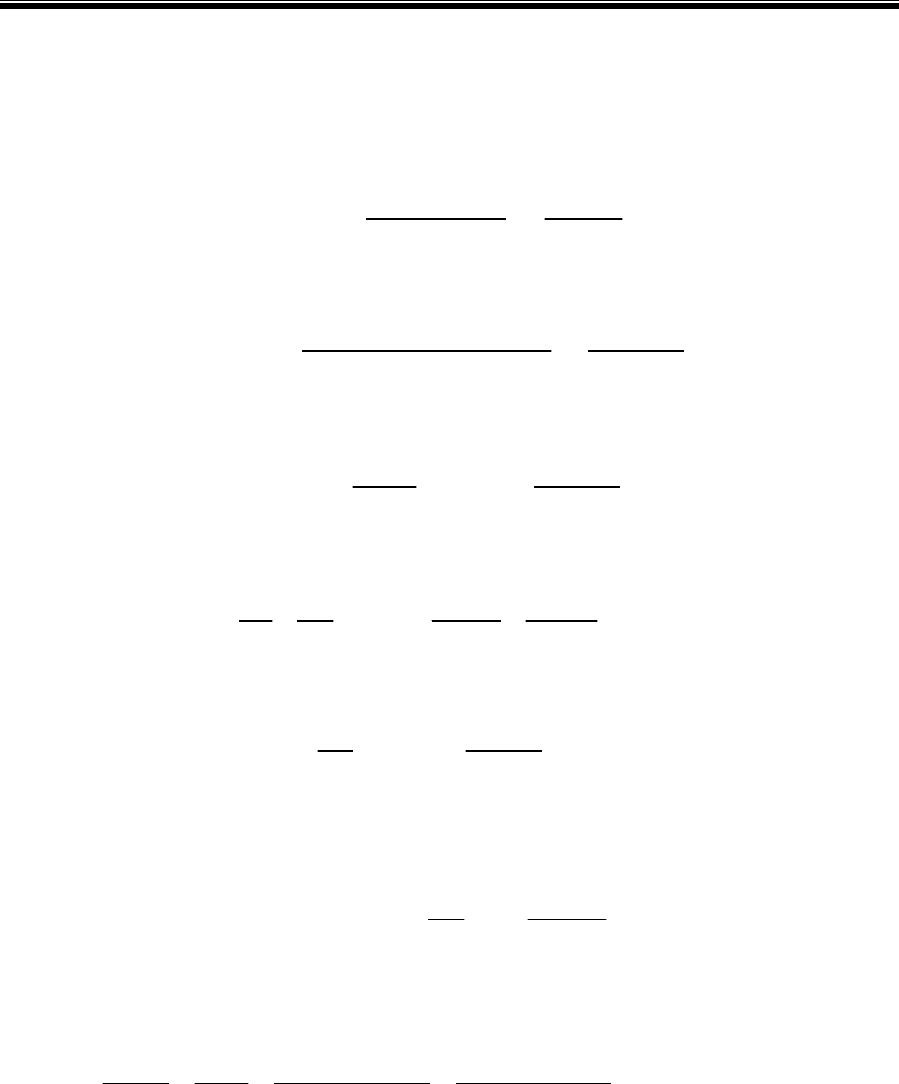
Часть I. Раздел 2. Особенности гидростатики вязкопластичных жидкостей (ВЖП)

Последний член уравнения – это давление, необходимое для уравновешива-

ния давления, вызванного разной плотностью жидкости в трубах и в заколон-

ном (затрубном) пространстве.

Определим давления р

1в

, р

2в

, р

1н

2в

11 1

вв в

вв

dl l

θθ

;

()

кп

Dd l

π+π θ

−

π−

Аналогично для второй секции:

;

кп

−

Подставив эти выражения в уравнение, найдем р

()

12 1 2

o вкп кпвк

вв

ll l l

dd DdDd

⎛⎞

=θ + +θ + +ρ−ρ

⎜⎟

−−

⎝⎠

. (2.2)

При i -том числе секций:

()

o вкп кпвк

iв i

dDd

=θ +θ +ρ−ρ

−

∑∑

. (2.3)

В частном случае – в процессе бурения – когда

=ρ

кп

=ρ, θ

=θ

кп

=θ, полу-

чим формулу:

iв i

dDd

⎛⎞

=θ +

⎜⎟

−

⎝⎠

∑∑

. (2.4)

Пример: l

=2800м; l

=200м; d

=0,127м; d

=0,178м; D=0,216м; θ=4 Па;

1в

=0,107м; d

2в

=0,08м.

2800 200 2800 200

4 4 1046273 1, 05 .

0,107 0,08 0, 216 0,127 0, 216 0,178

p Па МПа

⎛⎞

=⋅ + + + = =

⎜⎟

−−

⎝⎠

Из этого следует, что буровой раствор (при промывке скважины, а не при

цементировании) будет находиться в состоянии покоя до тех пор, пока давле-

ние на насосах не превысит 1,05 МПа.

Для практики бурения представляет большой интерес и другая задача, об-

ратная рассмотренной: определение "остаточного" давления на насосах р

ост

по-

сле того, как насосы плавно остановлены без открывания пусковой задвижки.

Дело в том, что при этом давление на насосах никогда не опускается до нуля

сразу. Если считать, что жидкость подчиняется модели Бингама, то будет спра-

Часть I. Раздел 2. Особенности гидростатики вязкопластичных жидкостей (ВЖП)

ведливо признать, что в данном случае р

ост

является величиной, эквивалентной

не θ, а τ

ост o

iв i

dDd

⎛⎞

=τ +

⎜⎟

−

⎝⎠

∑∑

, (2.5)

отсюда

ост

iв i

dDd

τ=

⎛⎞

⎜⎟

−

⎝⎠

∑∑

. (2.6)

Формулой (2.6) можно воспользоваться для ориентировочного определения τ

когда нет приборов для измерения реологических параметров, а формулой

iв i

dDd

θ=

⎛⎞

⎜⎟

−

⎝⎠

∑∑

, (2.7)

полученной из формулы (2.4), – для оценки СНС. Сравнение θ и τ

даст оценку

степени реологической нестационарности применяемой промывочной жидкости.

2.3. Определение высоты перепада уровней вязкопластичной

жидкости в трубах и заколонном пространстве при спуске

и подъеме колонны труб

Скважина и спущенная в нее колонна

нефтепромысловых труб (бурильные, об-

садные и насосно-компрессорные) образуют

систему сообщающихся сосудов, где одним

из сосудов является колонна, а

другим – за-

колонное пространство. Если бы скважина

была заполнена ньютоновской жидкостью,

например, водой, то при равенстве плотно-

стей жидкостей в обоих "сосудах" уровни

жидкости в них совпадали бы. Несколько

иначе обстоит дело, когда скважина запол-

нена вязкопластичной жидкостью (ВПЖ),

например глинистым раствором.

При медленном спуске (рис. 2.3) колонны

в скважину (медленном

для того, чтобы из-

бежать инерционных сил и влияния гидроди-

намических факторов) уровень жидкости в

трубах будет опускаться вместе с колонной и

после остановки колонны может оказаться

ниже устья скважины на величину h.

Рис. 2.3. Эффект снижения

уровня жидкости в трубах

при спуске

Часть I. Раздел 2. Особенности гидростатики вязкопластичных жидкостей (ВЖП)

Найдем наибольшее значение h, при котором ВПЖ в скважине еще может

находиться в состоянии покоя, не перетекая из заколонного пространства в

трубы (после спуск) или наоборот (после подъема). Обозначим диаметр сква-

жины через D, внутренний диаметр труб – d

, наружный диаметр – d

, длину

колонны труб в скважине – L

100

200 250 300 350 400

Диаметр скважины, мм

Снижение уровня жидкости в трубах при

спуске, м

СНС=0,001 Па

СНС=0,5 Па

СНС=1 Па

СНС=2 Па

СНС=3 Па

СНС=5 Па

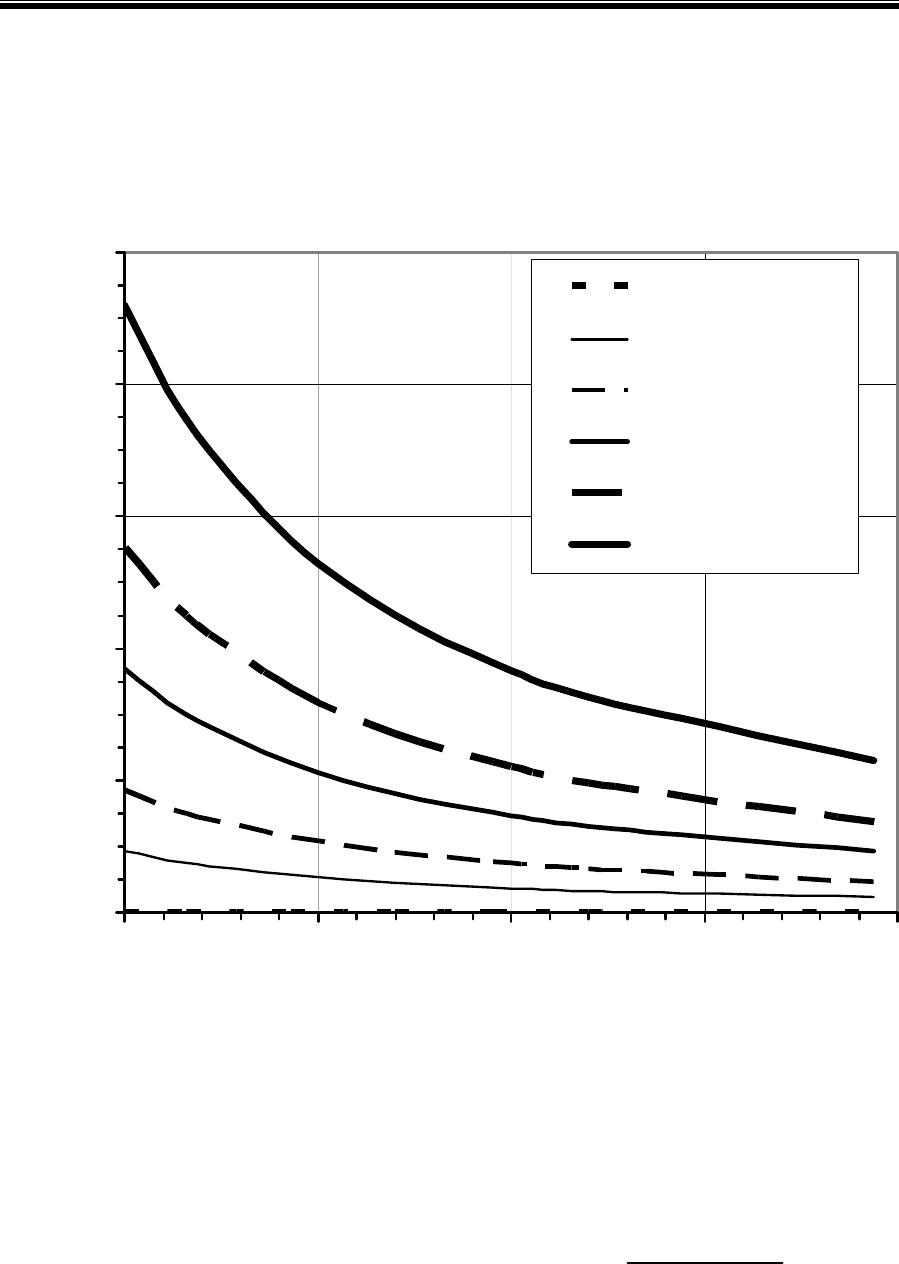
Рис. 2.4. Влияние диаметра скважины и СНС бурового раствора

на снижение уровня жидкости в бурильной колонне

диаметром 127 мм длиной 3000 м после ее спуска

Условие предельного равновесного состояния выразится уравнением:

()

(

)

вк нк к

dL h dL DL gh

π−

π−θ+πθ+πθ=ρ

Выразим h через другие величины: