Онищенко Г.Б. Электрический привод

Подождите немного. Документ загружается.

3. Скорость холостого хода при U

=220 В.

3,118

86,1

220

===

1/с

4. Добавочное сопротивление, вводимое в цепь якоря

ОмR

пуск

доб

86,177,0

5,335,2

220

=−

⋅

=−=

5. Максимальный момент при пуске

НмММ

нк

5,1552,625,25,2

⋅

6. Жесткость естественной механической характеристики

смкг

/.5,4

77,0

86,1

===

7. Жесткость пусковой механической характеристики

смкг

добя

/.32,1

86,177,0

86,1

8. Электромеханическая постоянная времени при работе на естествен-

ной характеристике

22,0

5,4

===

9. Электромеханическая постоянная времени при работе на пусковой

характеристике

мп

76,0

32,1

===

10. Электромагнитная постоянная времени при работе на естественной

характеристике

013,0

77,0

01,0

===

Поскольку Т

<<Т

то ею можно пренебречь.

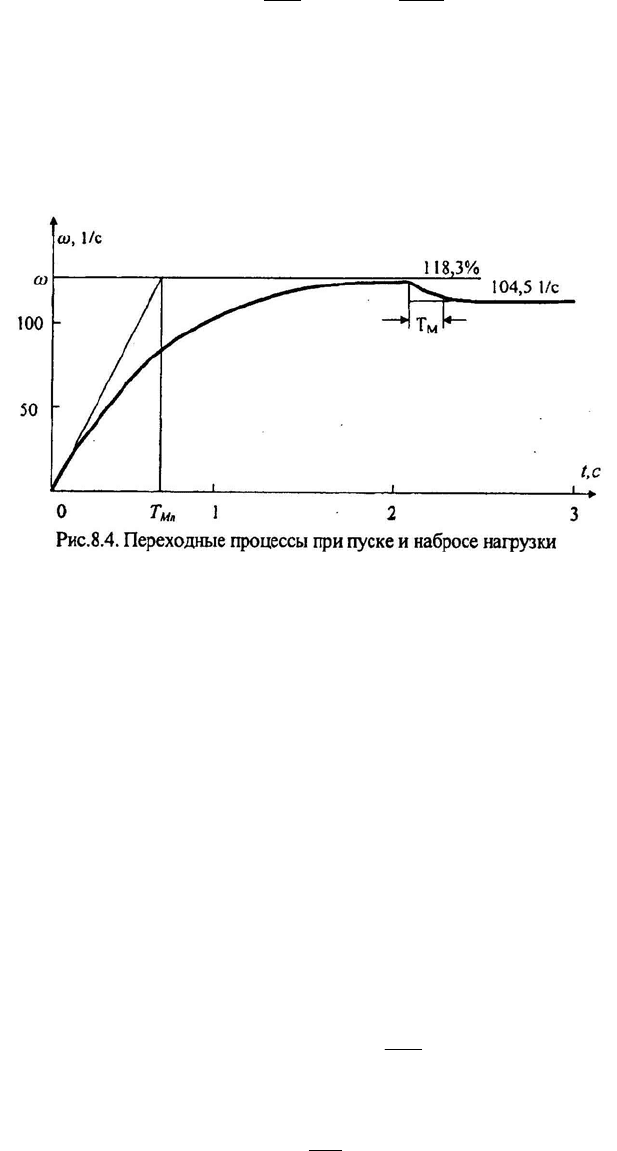
11.Построим характеристику переходного процесса при пуске вхоло-

стую по формуле (8.14)

()

ее

Мп

31,1

13,1181

−

−=

⎟

⎠

⎞

⎜

⎝

⎛

−=

ωω

12. По окончании переходного процесса пусковое сопротивление будет

закорочено, после чего к валу двигателя будет приложен момент М

=М

. По-

строить переходный процесс изменения скорости, связанный с приложением

нагрузки.

13.Установившееся значение скорости после приложения нагрузки

5,104

5,4

2,62

3,118

=−=−=

ωω

уст

1/с.

14. Построим характеристику переходного процесса при приложении

нагрузки по формуле (8.13)

ω= 104,5- (104,5 -118,3)е

-4,55t

Характеристики переходных процессов показаны на рис. 8.4.

8.3. Переходные процессы в электроприводе постоянного тока

Рассмотрим динамические характеристики электропривода постоянного

тока по системе тиристорный преобразователь - двигатель постоянного тока

(ТП-Д). Тиристорный преобразователь будем рассматривать как безынерцион-

ное звено с постоянным передаточным коэффициентом к

Электромеханические процессы при постоянном потоке возбуждения

описываются следующей системой уравнений (см. раздел 5.1):

JММ

СIМ

LRIСU

яяяя

=−

++=

(8-15)

Здесь С=кФ - машинная постоянная при неизменном потоке возбужде-

ния.

Электромагнитная и механическая инерционности двигателя отражают-

ся соответственно электромагнитной Т

и электромеханической Т

постоянны-

ми времени. Для двигателя постоянного тока

Т =

(8.16)

(8.17)

Решая уравнения (8.15) с учетом (8.16) и (8.17), получим

устмям

ТТ

ωω

=++

(8.18)

где:

МR

сяя

уст

−=

Полученное уравнение (8.18) является общим для двигателей с линей-

ной механической характеристикой, вид которой определяется величиной ее

жесткости β.

Переходя к операторной форме записи, полагая d/dt = р, получим ис-

ходную для построения структурной схемы систему уравнений

рТ

ММ

СIМ

рТRIСU

яяяя

)1(

=−

(8.19)

Данная система уравнений отражается структурной схемой двигателя

постоянного тока

независимого

возбуждения, состоящей

из четырех типовых

динамических звеньев

(рис.8.5).

Механическая часть двигателя характеризуется интегрирующим звеном

с постоянной времени Т

, величина которой определяется суммой момента

инерции якоря двигателя и моментами инерции всех движущихся частей рабо-

чей машины, приведенными к валу двигателя. Электромеханическое преобра-

зование энергии отражается пропорциональным звеном с коэффициентом пе-

редачи С, которое указывает, что момент двигателя пропорционален току яко-

ря. Электрическая цепь якоря двигателя представлена инерционным звеном с

постоянной времени Т

. Это звено характеризует, как изменяется ток якоря при

изменении разности напряжений (U

- Е

). Э.д.с. якоря Е

= кФω отражается в

виде отрицательной обратной связи. Такая связь является внутренней, т.к. она

соответствует природе физических процессов в описываемом объекте, а не соз-

дана системой регулирования.

Передаточная функция двигателя по управляющему воздействию при

регулировании скорости изменением напряжения якоря будет:

)(

→ рТрТТ

мям

(8.20)

Характер переходных процессов, определяется видом корней характе-

ристического уравнения (см. 8.18).

=++ рТрТТ

мям

(8.21).

Корни этого уравнения

ям

яммм

ТТ

ТТТТ

2,1

−±−

Если Т

>4Т

, то корни будут вещественными и отрицательными. В

этом случае решение уравнения (8.18) имеет вид:

tрtр

уст

еСеС

++=

ωω

(8.22)

Переходный процесс в этом случае будет носить монотонный характер

с изменением скорости по закону, соответствующем) инерционному звену вто-

рого порядка (см. рис.8.6).

Если T

< 4Т

, то корни будут комплексными сопряженными с отрица-

тельной вещественной частью р

1,2

= а ± jΩ , где

;

−

=Ω−=

(8.23)

Решение дифференциального уравнения (8.18) при этом будет:

уст

etCtС )sincos(

Ω+Ω+=

ωω

(8.24)

Постоянные интегрирования С

и С

находятся из начальных или ко-

нечных условий переходного процесса.

Переходный

процесс в этом случае

характеризуется перио-

дическими колебаниями

с частотой Ω и

затухающей

амплитудой. Время

переходного процесса ориентировочно может быть оценено, как t

= (6 —

10)Т

. Колебательность процесса связана с тем, что происходит периодическое

преобразование кинетической энергии в электромагнитную и обратно.

Выражение переходной характеристики для тока I

= f(t) может быть

получено из уравнения движения.

)(

⋅+=

(8.25)

т.е. ток является суммой двух составляющих: статического тока

CMI

/= и динамического тока, который пропорционален производной от ско-

рости (ускорению).

Передаточную функцию для тока при управляющем воздействии най-

дем из структурной схемы рис.8.5.

)(

рТрТТ

мям

яя

⋅=

→

(8.26)

где I

- статический ток, соответствующий статическому моменту.

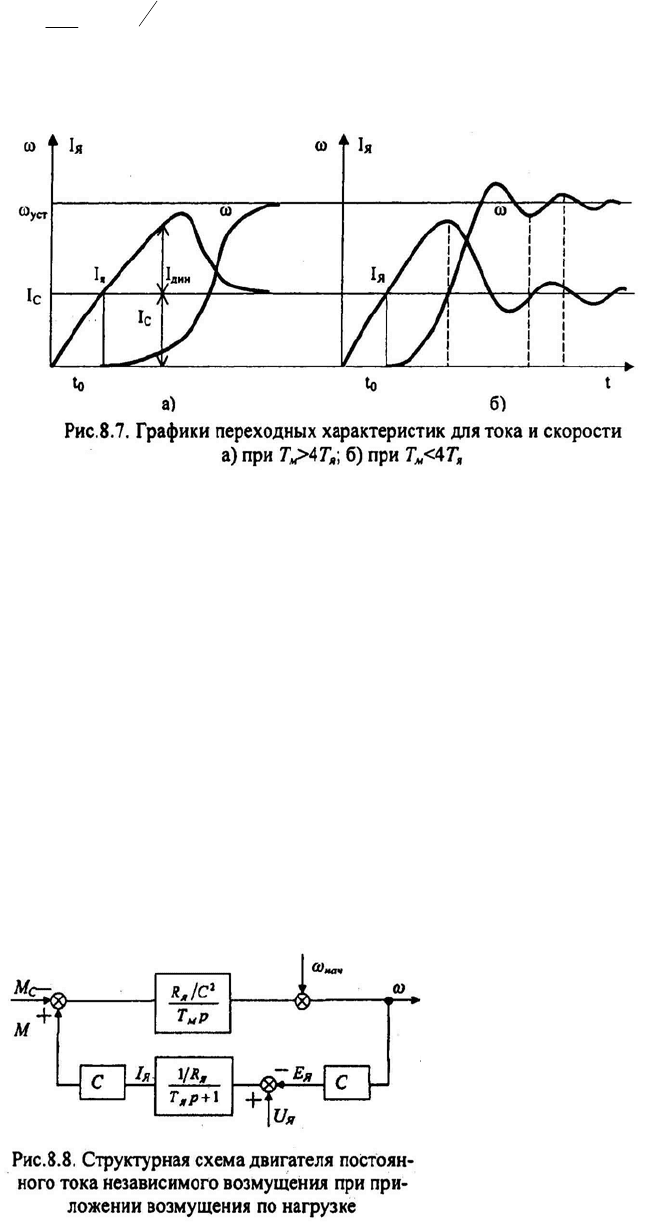
На рис.8.7 показаны переходные характеристики скорости и тока при

пуске двигателя до скорости

уст

ωω

Δ−= при наличии на валу двигателя ре-

активного статического момента; будем полагать, что в рассматриваемом слу-

чае Т

>4Т

. В течение времени t

(см. рис.8.7,а) ток якоря нарастает до значения

CMI

/= . Нарастание происходит по экспоненциальному закону

⎟

⎠

⎞

⎜

⎝

⎛

−=

−

1 .

Когда ток станет равным статическому, начинается движение вала

двигателя.

Динамический ток

возрастает, вследствие

чего растет ускорение

двигателя. Затем под

действием увеличи-

вающейся противоэ.д.с.

якоря ток начинает

спадать, и скорость двигателя асимптотически приближается к установившему-

ся значению.

Если Т

<4Т

, то в кривых тока и скорости появится колебательная со-

ставляющая (см. рис. 8.7,6).

Рассмотрим теперь динамические процессы при приложении нагрузки к

валу двигателя при постоянном напряжении, подводимом к якорной цепи дви-

гателя. Схема на рис.8.6 удобна для анализа переходных процессов по управ-

ляющему воздействию, когда изменяется U

. В нашем случае величина задания

скорости остается постоянной, а изменяется момент нагрузки М

. Для удобства

анализа процессов и нахождения

передаточной функции электропривода по

возмущающему воздействию преобразуем

структурную схему так, чтобы входным

воздействием являлся статический момент

, а выходным параметром - скорость ω.

Структурная схема для этого случая показана на рис.8.8. Примем, что двига-

тель работал вхолостую при М

=0 со скоростью СU

, ток якоря I

=0, так

что приложенное напряжение уравновешивалось э.д.с. якоря U

= Е

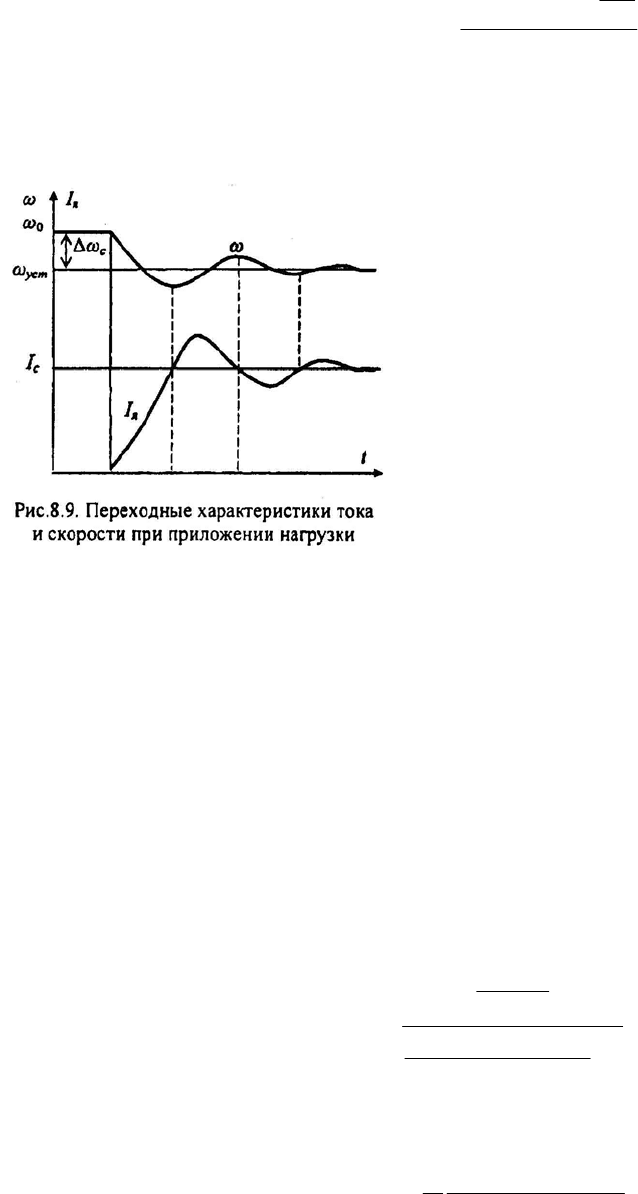
Если к валу двигателя скачком приложить нагрузку - статический мо-

мент М

=СI

, то скорость двигателя начнет снижаться, э.д.с. якоря будет умень-

шаться и в цепи якоря начнет нарастать ток (см. рис.8.9)

яя

LСU

−−

Если индуктивность якорной цепи велика (постоянная времени Т

), то нарастание тока будет отставать от темпа снижения скорости и к

моменту, когда скорость снизится до нового

установившегося значения

00 ссуст

−

, ток якоря еще не

достигнет величины I

, при которой момент

двигателя был бы равен моменту сопротив-

ления М

. Поэтому скорость будет

продолжать падать до тех пор, пока ток якоря

не станет равным статическому, затем

скорость начнет возрастать и после ряда колебаний достигнет установившегося

значения. Обратим внимание, что кривые ω = f(t) и I

= f(t) взаимосвязаны -

точкам максимума и минимума скорости, когда dω/dt = 0, соответствует мо-

мент пересечения кривой тока линии статического тока.

Если индуктивность якорной цепи невелика Т

, то процесс сни-

жения скорости при приложении нагрузки будет иметь монотонный характер.

При постоянной величине U

передаточная функция электропривода по

возмущающему воздействию будет

)1(

)(

⋅

−=

Δ→

рТрRТС

ССR

рТС

яям

, (8.27)

Выполнив преобразования, получим:

)(

−=

Δ→

рТрТТ

рТ

мям

(8.28)

где

RС /

- жесткость механической характеристики

электропривода.

Из выражения (8.28) следует, что при приложении нагрузки М

ско-

рость двигателя снизится на величину ∆ω

. По окончании переходного процес-

са (р=0) установившаяся ошибка будет

=Δ

т.е. установившаяся величина снижения скорости (статическая ошибка

∆ω

) пропорциональна величине приложенного момента и обратно пропорцио-

нальна жесткости механической характеристики электропривода.

Как уже отмечалось в главе 4, для повышения точности регулирования

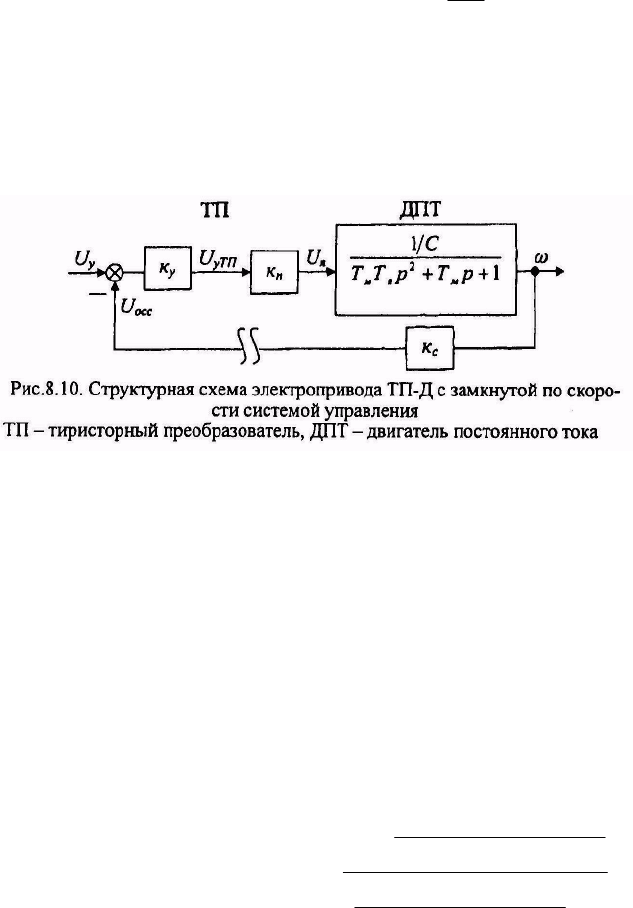
скорости применяются замкнутые системы регулирования с обратной связью

по скорости. Структурная схема электропривода по системе ТП-Д с обратной

связью по скорости представлена на рис.8.10. Тиристорный преобразователь

будем рассматривать как безинерционное звено с передаточным коэф-

фициентом к

. Передаточная функция по управляющему воздействию, состав-

ленная по схеме рис.8.10, будет:

)1(

)(

→

рТрТТС

ккк

рТрТТС

кк

мям

спу

мям

пу

Обозначим (к

)/С = К - коэффициент усиления разомкнутой систе-

мы (при разрыве обратной связи по скорости).

Тогда после преобразований получим:

)1(

)(

→

рТ

Кк

(8.29)

Передаточная функция показывает, что в замкнутой по скорости систе-

ме регулирования электромеханическая постоянная времени Т

, характери-

зующая инерционность механической части электропривода, как бы уменьша-

ется в (К+1) раз. Это связано с тем, что жесткость механических характеристик

β в замкнутой системе увеличивается в (К+1)раз, что было показано в разделе

Это важное свойство - повышение быстродействия привода, - которое

дает отрицательная обратная связь по скорости, сопряжено с существенным

недостатком - возрастанием колебательности переходных процессов.

Обычно электромеханическая времени Т

больше, чем 4Т

, и в разомк-

нутой системе регулирование скорости во времени переходных процессов ко-

лебания не наблюдаются. Введение отрицательной обратной связи по скорости

уменьшает эквивалентную электромеханическую постоянную времени, причем

чем больше коэффициент обратной связи к

, тем меньше Т

м.экв

. Поэтому в замк-

нутых по скорости системах регулирования Т

м.экв

становится меньше 4Т

, и пе-

реходные процессы в электроприводе приобретают колебательный характер.

Для снижения колебательности в систему регулирования вводятся корректи-

рующие звенья. Способы формирования переходных процессов требуемого ха-

рактера рассмотрены в главе 10.

В общем случае можно предложить следующий порядок анализа пере-

ходных процессов в системах электропривода, если эти процессы описываются

линейными (или линеаризованными)

дифференциальными уравнениями.

1. Определяется, какие инерционности следует учитывать при анализе

данного переходного процесса.

2. Находят постоянные времени, характеризующие каждую инерцион-

ность. Если постоянные времени отличаются на 2 и более порядка, то меньши-

ми в инженерных расчетах, как правило, можно пренебречь.

3. Число инерционностей определяет порядок дифференциального

уравнения, описывающего переходный процесс.

4. Находят характеристическое уравнение, соответствующее левой час-

ти однородного линейного дифференциального уравнения, описывающего ис-

следуемый переходный процесс (см., например, (8.18)).

Переходный процесс в случае линейных зависимостей переменных и

скачкообразного (единичного) характера управляющего или возмущающего

воздействий будет описываться уравнением х = f(t), (где х - исследуемый

пара-

метр электропривода - ток, момент, скорость).

Задача 8.2. Определить, какой характер будут иметь переходные про-

цессы в электроприводе ТП-Д с разомкнутой и замкнутой по скорости систе-

мами регулирования.

Основные данные приводного двигателя постоянного тока: номиналь-

ное напряжение якоря U

ян

=220 В; сопротивление якорной цепи R

=0,6 Ом; ин-

дуктивность обмотки якоря L

=0,02 Гн; машинная постоянная C=l,9 В.c.; но-

минальная скорость ω

=104,5 1/с. Момент инерции привода L

=1,0 кг.м

Данные по системе управления U

изменяется от 0 до 10В; изменению

напряжения тиристорного преобразователя от 0 до 300В линейно соответствует

изменение напряжения, подаваемого на систему управления ТП - от 0 до 30В;

коэффициент обратной связи по скорости к

=0,09В.с.

Решение

1. Электромагнитная постоянная времени якорной цепи

033,0

6,0

02,0

===

2. Электромеханическая постоянная времени

16,0

9,1

6,01

⋅

3. Коэффициент усиления усилителя кур в разомкнутой системе

2,2

300

220

===

ун

уТПн

ТПн

ян

ур