Одинцов Б.Е. Обратные вычисления в формировании экономических решений: Учеб. пособие

Подождите немного. Документ загружается.

Представим эту задачу в виде системы уравнений:

АВ а

АС ~ Р'

Решив ее относительно АВ и АС, получим:

АВ =

-АС,

АС:

^-1

Проверка, а

0,7; Р = 0,3; 5 = 20; С =

12;

Я = 8; АЯ = 4; АС = 3;

А5 = 7;5 + А5 = 27;С + АС=

15;

Я + АЯ = 27 - 15 = 12.

Какими граничными значениями должны обладать Ау, а и (3,

чтобы задача имела решение, укажет система следующих нера-

венств:

-АС>0,

АА

^-1

>1.

Одним из очевидных ограничений является неравенство

а>р.

В качестве примера здесь использована аддитивная функция,

для которой отыскивались приросты с одинаковыми знаками. В

п. 1.3 было показано, что в таких частных случаях задачу можно

решить путем пропорционального деления прироста функции и

добавления результатов деления к ее аргументам. Этого не сде-

лано с целью демонстрации общности метода обратных вычис-

лений без коэффициентов прироста аргументов.

16.

Целевая установка:

j"^

= /(jc"^(a), z (P)).

Задача обратных вычислений принимает вид:

у + Ау =

f{x

Ах,

Z -

Лх _ а

Az),

Пример (рис. 2.14). Воспользуемся примером из целевой ус-

тановки 2, в которой рентабельность Р рассчитывается делением

прибыли и на себестоимость продукции С. Пусть целевая уста-

новка остается прежней, т.е. необходимо увеличить рентабель-

ность за счет повышения прибыли и снижения себестоимости,

причем большая часть увеличения рентабельности должна про-

изойти за счет повышения прибыли, а меньшая - за счет сниже-

ния себестоимости. Такая целевая установка представляется сле-

дующим образом:

р+ =

Я+(а)

Составим систему уравнений:

а>|3.

Р + АР =

+ АП

С-АС'

АП а

дс~р'

Решив ее относительно АП и АС, получим:

АС

{Р +

АР)С-П

Р+АР+-

АП

аДС

Неравенствами для поиска приемлемых диапазонов исходных

данных служат выражения: АС >

и АП

Проверка, а

0,7; Р = 0,3; Я = 24; С = 4; Р = 6; ДР = 4; ДС = 1,3;

ДЯ=3;Я + ДЯ = 27;С + ДС = 2,7; Р+^

—

10.

17.

Целевая установка:

j"*"

= f{x (а), г"^(Р)).

Задача обратных вычислений принимает вид:

[>'

+ Ау

= /(х -

Ах,

Az),

Ах _ а

пример (рис. 2.15). Прибыль Я^, направляемая на потреб-

ление, и прибыль Я , направляемая на инвестиции, составляют

общую прибыль, равную

П^П^+П^,

где Я- общая прибыль.

Необходимо определить, какими должны быть величины Я^

и Я^, чтобы Я увеличилась на величину АЯ. Прибыль Я^ должна

снизиться, а прибыль Я^ - увеличиться. Большая часть АЯ долж-

на возникнуть за счет увеличения Я^, а меньшая - за счет Я^. Та-

кая целевая установка отражается следующим образом:

Я^=Я-(а)-1-ЯЛР), а<р.

40(47)

О.з/

/е

\р

0,7

Ли =

/=1.3(1,5)

а = 0,3/

/е

\р = 0,7

А=15

Рис.

2.15

Рис.

2.16

Представим эту задачу в виде системы уравнений:

Я+АЯ

(Я„-ДЯ„)

(Я„+АЯ„),

АЯп_а

Решив ее, получим:

дя„

А П

А/7и

_ Ml

^-«'

Очевидным ограничением служит выражение а < р.

Проверка, а = 0,3; р = 0,7; П^^ \0; П^ = 30; Я = 40; АЯ = 7;

ДЯ^ = 5,26; ДЯ^ = 12,28; Я^ - ДЯ^ = 10 - 5,26 = 4,74; Я^ + ДЯ^ =

= 30 + 12,28 = 42,28; П-^ АП

4,74 + 42,28 = 47,02 - 47."

18.

Целевая установка: у'^ = /(л:~(а), г~(Р)).

Задача обратных вычислений принимает вид:

{y-hAy

f(x -Ax,z-

Az),

AJC

_ a

Как правило, Задача имеет решение при а < р.

Пример (рис. 2.16). Индекс прибыли рассчитывается по

формуле

где / - индекс прибыли;

Б - прибыль базового периода;

А - прибыль анализируемого периода.

Необходимо поднять индекс за счет снижения прибыли как в

базовом, так и в анализируемом периодах. Большая часть сниже-

ния должна произойти за счет снижения прибыли в анализируе-

мом периоде. Такая целевая установка отразится следующим об-

разом:

А-ФУ

Запишем систему уравнений:

А/

Б-АБ

А-АА'

АБ а

М ~р'

Решив данную систему, получим:

^^ЛЦ.АР-Б^^^а^

Проверка. Б = 20; А = 15; / = 1,3; А/ = 0,17; а = 0,3; (3 = 0,7;

АА = 2,31; АБ = 0,99; Б - АБ = 20 ~

0,989

19,01;

А - АЛ = 15-

2,31 = 12,69; /4-А/:

19,01

12,69

= 1,498 «1,5.

Теперь рассмотрим задачи, решение которых позволяет сни-

зить значение функции.

19.

Целевая установка: у'^ = /(jc"*"(a), г^(Р)).

Задача обратных вычислений принимает вид:

у-Ау

f{x

Лх,

Z +

Az),

Лх _ а

Az~p^'

Пример (рис. 2.17). Воспользуемся зависимостью из целе-

вой установки 1, где прибыль П рассчитывается на основе вы-

ручки В и себестоимости продукции С. Расчет выполняется по

формуле

В-С.

Целевая установка состоит в следующем: необходимо снизить

прибыль, однако выручка и себестоимость должны повыситься.

При этом большая часть снижения прибыли должна произойти

за счет повышения себестоимости. Такая целевая установка от-

ражается следующим образом:

Я~

= 5'^(а)-С"^(р),р>а.

8(4)

О.з/

\р

0,7

С=12

20(18)

0,з/

/®

\р

0.7

Л„ = 8

Рис.

2.17

Рис.

2.18

Составим систему уравнений:

{П-АП

АВ-(С-АС),

АВ а

Решив ее относительно АВ и АС, получим:

^,ДС

-^.

1--

Ограничением служит выражение ^

<1.

Проверка, а

0,3; Р = 0,7; 5 = 20; С =

12;

Я = 8; ДЯ = 4; АС = 7;

А5 = 2,99;5 + А5 = 22,99;С + АС=19;Я-ДЯ = 22,99-19 = 3,99-4.

20.

Целевая установка: у~ = /(л:^(а), г~(р)).

Задача обратных вычислений принимает вид:

^у-Ау

f(x

-I-

Ах,

Az),

Ах _ а

[А^~Р*

Пример (рис. 2.18). Прибыль Я^, направляемая на потреб-

ление, и прибыль Я , направляемая на инвестиции, составляют

общую прибыль Я, равную

П„-^П^.

Целевая установка следующая: необходимо снизить общую

сумму прибыли, причем большая часть отрицательного прирос-

та прибыли должна быть обеспечена за счет увеличения прибы-

ли,

направляемой на потребление, и меньшей - за счет прибыли,

направляемой на инвестиции. Такая целевая установка запишет-

ся следующим образом:

Я-

= я;(а)

ЯЛР).

Это позволяет сформулировать следующую задачу обратных

вычислений:

Я-АЯ

Я„+АЯ„+(Я„-ДЯ,),

ЛЯ„ а

1АЯ„ р

Решив ее, получим:

АЯ„

аАЯ.

АЯ =-

АЯ

-1

Ограничением служит выражение а < р.

Проверка, а = 0,3; р = 0,7; П^ = 12; П^ = 8; Я = 20; ДЯ = 2;

АЯ = 3,5; АЯ = 1,5; Я + АЯ ="l2 + 1,5^= 13,5; Я - АЯ =8-

и''п''п

п ' ''и и

-3,5 = 4,5;Я-АЯ= 13,5 + 4,5 = 18.

21.

Целевая установка:

j""

= /(д:~(а), г"^(Р)).

Запишем задачу обратных точечных вычислений:

у-Ау

f(x -

Ах,

Z +

Az),

Ах _ а

AJ~P'

Пример (рис. 2.19). Воспользуемся целевой установкой 20,

но изменим знак первого аргумента на минус, а второго - на плюс.

Кроме того, большая часть отрицательного прироста функции

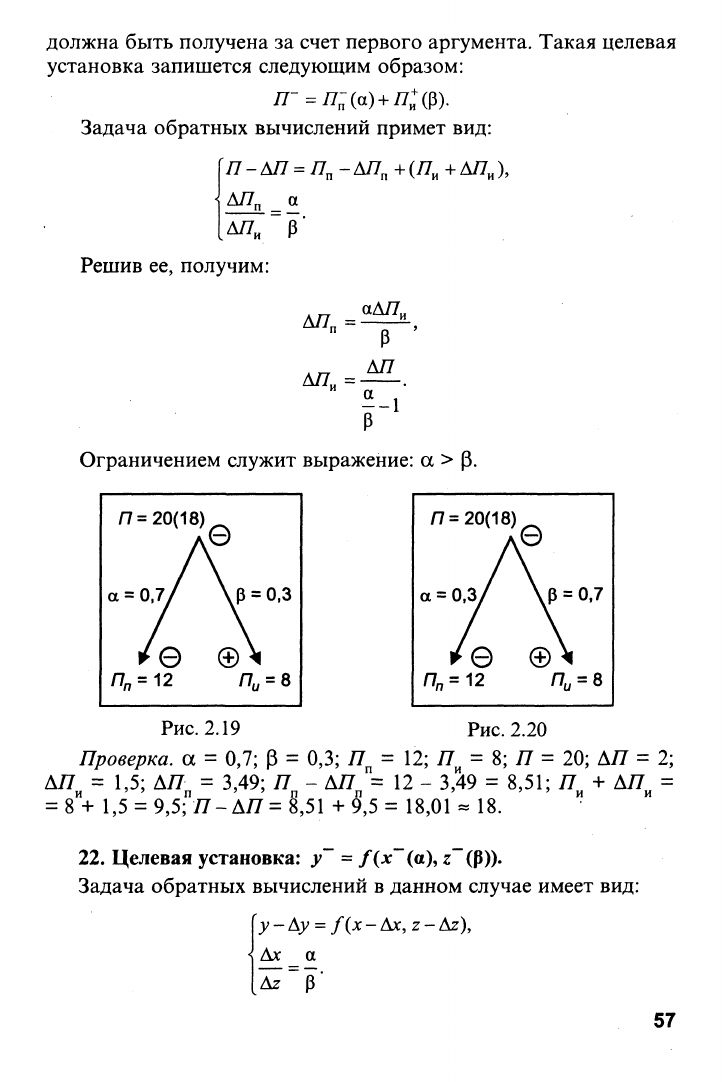
должна быть получена за счет первого аргумента. Такая целевая

установка запишется следующим образом:

Я-

Я„-(а) +

я:(р).

Задача обратных вычислений примет вид:

Я-АЯ = Я„ -АЯ„ +(Я„ +АЯ„),

АЯ„ а

Решив ее, получим:

АЯ =

аАЯи

ДЯ

-1

Ограничением служит выражение: а > р.

20(18)

0,7

Р =

0,3

ЛГ =

20(18)

0,3

Р =

0,7

Л„=12

Рис.

2.19 Рис. 2.20

Проверка, а = 0,7; Р = 0,3; Я„ = 12; Я^ = 8; Я = 20; ДЯ = 2;

ДЯ = 1,5; ДЯ = 3,49; Я - ДЯ "= 12 - 3,49 = 8,51; Я + ДЯ =

и''п''п

п ' ''и И

= 8+ 1,5 = 9,5; я-АЯ= 8,51 +9,5 = 18,01^18.

22.

Целевая установка: у

f{x (а), z (Р)).

Задача обратных вычислений в данном случае имеет вид:

(у-Ау

f(x -

Ах,

Az),

Ах _ а

А^~|Р*

Пример (рис. 2.20). Воспользуемся примером из целевой ус-

тановки 20, но изменим знак обоих аргументов на минус. Кроме

того,

будем считать, что большая часть отрицательного приро-

ста функции должна быть получена за счет второго аргумента.

Такая целевая установка запишется следующим образом:

П-=П-(а)^П-ф).

Рассматриваемая задача примет вид:

АП„ а

Решив ее, получим:

АЯ„ «^"

АЯ =-

АП_

Проверка, а = 0,3; Р = 0,7; П^= \2; П^ = i; П = 20; Ml = 2;

MI =

1,399;

ДЯ =0,599; Я -Ml = 12-0^599 = 11,4; Я -ДЯ =

и''п''п

п ' ''и И

8-1,399

= 6,6;Я-АЯ= 11,4 + 6,6= 18.

Эта задача содержит аддитивную функцию и одинаковые зна-

ки приростов, поэтому она может быть решена также простым

делением прироста функции между аргументами (см. п. 1.3).

2.4.

Решение задач без указания

приоритетности целей

Достаточно часто важность целей установить или невозмож-

но,

или затруднительно. Иногда такая характеристика не инте-

ресует лицо, формирующее решение. Например, если у функции

7-10 аргументов, то определить важность целей, отражаемых с

их помощью, весьма проблематично. Существуют специально

разработанные для этого методы, например, метод анализа иерар-

хий Саати, однако этот и другие методы требуют значительных

дополнительных усилий [7]. Очень часто перед лицом, формиру-

ющим решение, стоит задача добиться цели без указания каких-

либо приоритетов в путях ее достижения. В таких случаях задача

обратных точечных вычислений упрощается и сводится к реше-

нию уравнений с одним неизвестным. Им служит единый коэф-

фициент, на который следует либо умножить, либо разделить

исходные значения аргументов, чтобы получить желаемый при-

рост функции.

Как и ранее, функция дополняется целевыми установками,

однако КОВ отсутствуют.

Пусть задана функция

=/(л:, ^)- Как и ранее, в соответствии

с целевыми установками возникают следующие варианты обрат-

ных точечных вычислений:

/=/(x*,z*).

Как видим, КОВ отсутствуют.

23.

Целевая установка: у'^ = /(JC"*", Z^).

Если ввести единый коэффициент к, то можно получить:

х-{-Ах

кх;

z-\-Az

kz.

Задача обратных вычислений примет вид:

у + Ау =

f(kx, kz).

Пример (рис. 2.21). Воспользуемся задачей из целевой уста-

новки

где речь шла об исчислении прибыли по формуле П

В-С,

dLlT—

прибыль; В - выручка; С - себестоимость продукции.

Допустим, целевая установка состоит в следующем: необходи-

мо повысить прибыль за счет увеличения выручки и себестоимо-

сти.

Такая целевая установка представляется следующим образом:

Представим эту задачу в виде выражения:

+ АП = В +

АВ-(С-^АС1

Введем величину к и запишем:

В + АВ =

кВ,

+ АС =

кС.

АП=^кВ~кС

к(В-СХ