Никитин Г.И. Помехоустойчивые циклические коды

Подождите немного. Документ загружается.

скольку при m = 11 примитивный код БЧХ имеет длину n = 2

- 1 = 2047, причём это зна-

чение без остатка делится на длину кода Голея n = 23 (2047 : 23 = 89), который отно-

сится к непримитивным БЧХ- кодам [5, 6].

На основании данных табл. 3 можно построить графики зависимости скорости

передачи В

= k / n от значения скорости исправления ошибок ν= g

/ n , которые при-

ведены в [6]. Если отношение g

/ n остается постоянным, то скорость передачи В

стре-

мится к нулю, когда n неограниченно возрастает.

Как отмечалось выше, все примитивные коды БЧХ обладают конструктивным

расстоянием d

min

≥ 2g

+1. Расстояние можно увеличить до 2g

+ 2. Для этого нужно основ-

ной порождающий полином БЧХ - кода домножить на бином X+1, т.е. G

(X) = (Х+1)

×G

БЧХ

(X), что повлечёт за собой прибавление к коду одного проверочного символа,

обеспечивающего проверку на чётность всех символов БЧХ - кода. Таким образом полу-

чается расширенный БЧХ - код.

Адекватно можно получить укороченный (усечённый) БЧХ - код, следуя алгорит-

му, изложенному в подразделе 1.6.

Коды Рида—Соломона (PC) являются важным и широко используемым подмно-

жеством кодов БЧХ. Двоичный код Рида—Соломона получится, если взять основание ко-

да q = 2

. Это означает, что каждый символ кода заменяется s -значной двоичной после-

довательностью. Если исходный код с основанием q исправляет ошибки кратности < g

то полученный из него двоичный код имеет 2g

·s проверочных символов (по 2g

на каж-

дый блок из символов) из общего числа n = s ·(2

- 1). Код может исправлять серийные

ошибки (пакеты ошибок) длиной ≤ b = s ·( g

-1)+1 .

Коды PC, наряду с кодами Файра (4.10), являются наиболее подходящими для ис-

правления серийных ошибок, а также в каскадных системах кодирования в качестве

внешних кодов.

Построение кодеров и декодеров ЦК основывается на применении ЛПС, содер-

жащих сдвигающие регистры. Как отмечает Р. Блейхут [5], ЛПС "были сразу использова-

ны большинством исследователей и вошли в литературу без всяких фанфар."

1.8. Структурный состав линейных переключательных схем

Цикличность перестановок при формировании разрешённых кодовых комбинаций

ЦК лежит в основе техники построения кодирующих устройств (КУ) и декодирующих уст-

ройств (ДУ) циклических кодов. Эта техника применяет сдвигающие регистры (СР) в виде

триггерных цепочек с теми или иными обратными связями. Такие СР называют также

многотактными линейными переключательными схемами (ЛПС) и линейными кодовыми

фильтрами Хафмена, который первым начал изучение ЛПС с точки зрения линейных

фильтров. Кстати, Д. Хафмен является и автором принципа, состоящего в том, что "две

точки зрения лучше, чем одна", получившего широкое применение в настоящее компро-

миссное время.

При построении ЛПС используется 3 вида элементарных устройств:

1) сумматор, имеющий, как правило, два входа и один выход, причём

для двоичных кодов суммирование осуществляется по модулю 2;

2) ЗУ, имеющее один вход и один выход и представляющее собой одну

триггерную ячейку (один разряд) СР;

3) устройство умножения на постоянную величину, имеющее один вход

и один выход. Эти устройства изображаются на схемах так, как показано на рис. 4.1.

Линейными переключательными схемами с конечным числом состояний на-

зываются любые схемы, содержащие конечное число сумматоров, устройств памяти и

устройств умножения на константу, соединённых любым допустимым способом.

В бинарном случае сумматор (равно как и вычитатель) представляет собой ло-

гический элемент "исключающее ИЛИ", а устройство памяти является устройством

задержки (D-триггером). Устройства задержки, включённые последовательно, состав-

ляют СР, в ячейках которого выходной символ совпадает с входным символом в

предшествующий момент времени. К СР подводится шина сдвига, с помощью кото-

рой тактовыми импульсами (ТИ) осуществляется продвижение по разрядам СР запи-

санной кодовой информации. Как правило, шина сдвига не показывается на схемах с

изображениями ЛПС.

При формировании и обработке двоичных ЦК введение в схему ЛПС умножителя

на константу, равную 1, эквивалентно введению дополнительного соединения, а

умножитель на константу, равную 0, соответствует отсутствию такого соединения.

Предполагается, что на вход СР, входящего в состав ЛПС, кодовая ком-

бинация подаётся последовательно, с периодичностью, равной периоду следования ТИ

в шине сдвига. Аналогично, последовательно во времени, появляются кодовые сим-

волы на выходе СР. Когда входом или выходом является многочлен, представляющий

при двоичной обработке набор " 1" и "0", то на входном или выходном конце СР появ-

ляются только коэффициенты (" 1" или "0"), начиная с коэффициентов высших поряд-

ков. Это обуславливается тем, что при делении у делителя сначала должны быть

обработаны коэффициенты высших порядков.

В последующих разделах описываются схемы, используемые для умножения

и деления любых многочленов на некоторый фиксированный, в частности, порождаю-

щий полином.

1.9. Умножение полиномов на базе ЛПС

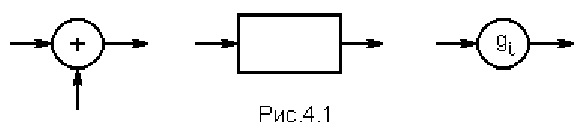
Схема, изображенная на рис. 4.2, используется для умножения любого полинома

на входе

A(X) = a

+ a

X + a

… + a

на фиксированный полином, в частности, порождающий:

G(X) = g

+ g

X + g

… + g

Предполагается, что первоначально все разряды СР содержат нули, а на

вход коэффициенты полинома А(Х) поступают, начиная с коэффициентов высших

порядков (со старших разрядов), после чего следует r нулей.

Первый вариант ЛПС для умножения полиномов (рис. 4.2).

Произведение полиномов

A(X)·G(X) = a

+(a

+ a

)X + ... + a

k+r

.(4.32)

Когда на входе ЛПС появляется первый (старший) коэффициент поли-

нома А(Х), то он умножится в первом устройстве умножения на g

и появится на вы-

ходе уже как результат перемножения a

, проследовав "транзитом" через все схемы

суммирования по модулю 2. Кроме того, a

запишется в первом разряде СР, а все ос-

тальные разряды СР будут содержать нули. Спустя единицу времени, с появле-

нием в шине сдвига 2-го ТИ, на входе появится a

k-1

, который перемножится с g

и сложится в первой схеме суммирования по модулю 2 с a

r-1

, сформировав на

выходе сумму a

k-1

+ a

r-1

, т. е. второй коэффициент произведения A(X)·G(X). Даль-

нейшие операции производятся аналогичным образом. После r+k сдвигов СР

полностью обнуляется и на выходе появляется значение a

, равное первому ко-

эффициенту произведения (4.32), так что произведение на выходе ЛПС последова-

тельно получается в полном составе.

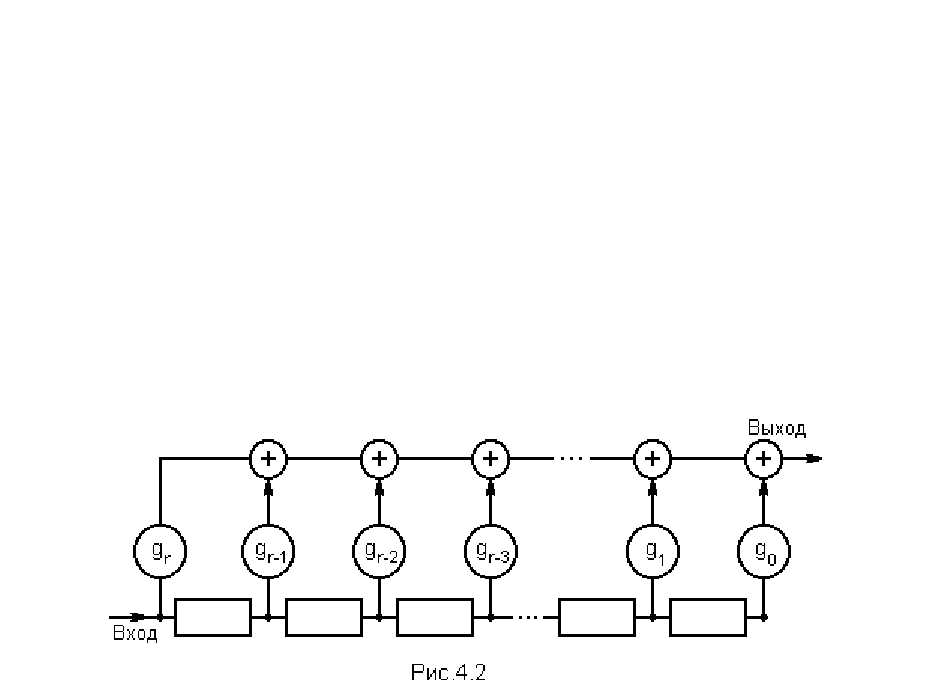
Второй вариант ЛПС для умножения полиномов показан на рис. 4.3.

Коэффициенты произведения формируются непосредственно в СР. После

того, как первый символ подаётся на вход, на выходе появляется последний коэффи-

циент (4.32) a

, а разряды СР содержат только нули. После одного сдвига ячейки

СР содержат элементы a

, a

,..., a

r-1

, a вход равен a

k-1

. При этом выход СР равен

r-1

+ a

k-1

, т. е. равен второму коэффициенту (4.32). После появления очередно-

го ТИ в шине сдвига (не показана на рис. 4.2 и 4.3) на выходе появляется третий

коэффициент (4.32). Дальнейшие операции производятся аналогичным образом.

Схемы умножения могут иметь более чем один вход, если добавить к ЛПС, изо-

браженной на рис. 4.3, вторую шину с цепочкой устройств умножения, связанных с

соответствующими схемами суммирования по модулю 2. Тогда схема будет реали-

зовывать процедуру суммирования произведений двух пар полиномов

C(X) = A

(X)·G

(X) + A

(X)·G

(X) , (4.33)

причём ЗУ в виде СР будет только одно.

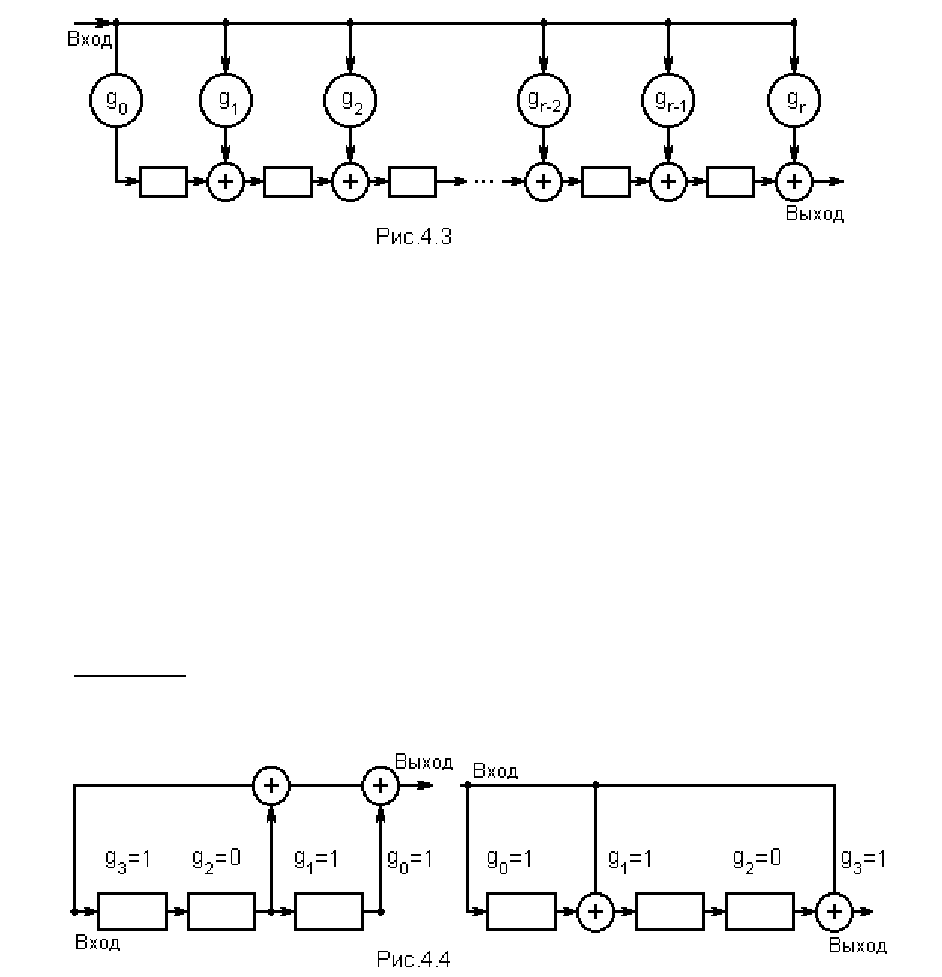
Пример_5. Составить 2 схемы кодирующих устройств ЦК Хемминга (7, 4) на базе

двух рассмотренных вариантов ЛПС для умножения полиномов (рис. 4.4). В качестве

порождающего полинома использовать полином G (7,4) = Х

+ X +1 (см. примеры 1 и 3).

Напомним (см. подраздел 1.4), что применение в кодерах метода умножения

приводит, к сожалению, к формированию неразделимых ЦК.

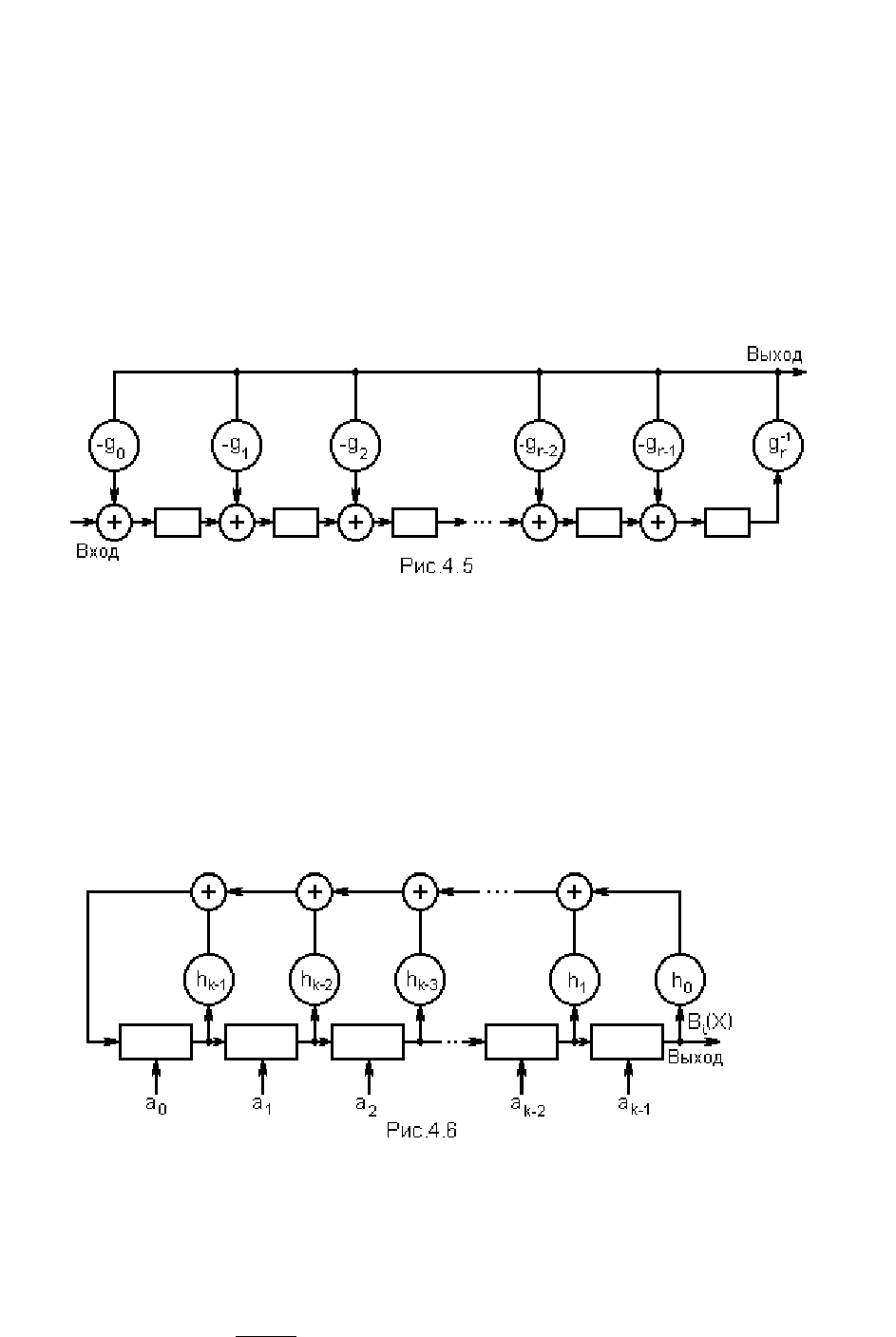
1.10. Деление полиномов на базе ЛПС

Схема для деления полинома A(X) = a

+ a

X + a

… + a

на полином

G(X) = g

+ g

X + g

… + g

представлена на рис. 4.5. Динамическое ЗУ в виде СР

вначале должно содержать все нули. Для деления полиномов СР охвачен обратной

связью, т. е. выход СР соединяется со входом. Для подчёркивания противополож-

ного направления шины обратной связи коэффициент умножителя обозначается

как g

-1

. Однако для двоичных кодов результат умножения и деления на единицу

одинаков, поэтому указанное обозначение в дальнейшем использоваться не будет.

Первый вариант Л ПС для деления полиномов (рис.4. 5).

Для первых r - сдвигов, т, е. до тех пор, пока первый входной символ не дос-

тигнет конца PC, выход принимает значения, равные "0". После этого на выходе появля-

ется первый ненулевой выход, который равен a

·g

-1

- первому коэффициенту частного.

Для каждого коэффициента частного g

необходимо вычесть из делимого полином

G(X). Это вычитание производится с помощью обратной связи. После k сдвигов на вы-

ходе появится частное от деления, а остаток от деления будет находиться в PC.

Работу схемы легче всего понять с помощью примеров построения КУ и ДКУ

на базе ЛПС, рассматриваемых далее в разделе 1.11.

Второй вариант ЛПС с делением на генераторный полином (рис. 4.6).

При построении КУ ЦК, а также генераторов различных кодовых последо-

вательностей, в частности, последовательностей максимальной длины (М-

последовательностей), применяется в ряде случаев так называемый генераторный

полином Н(Х). Этот полином называют также проверочным, если он получается при

делении бинома 1+Х

на порождающий полином G(X):

)X(G

)X(H

= (4.34)

При использовании этой схемы в качестве КУ ЦК исходную кодовую комбинацию

А(Х) параллельно, одновременно записывают в k разрядов СР.

С первым тактом на выход будет выдан коэффициент b

n-1

= a

k-1

, произойдет сдвиг

вправо в СР, и в освободившуюся ячейку памяти будет записано вычисленное значе-

ние проверочного бита r

n -k-1

= h

k-1

+ h

k-2

+ ... + h

k-1

. Со вторым тактом на выход бу-

дет считан коэффициент b

n-2

= a

k-2

, произойдет сдвиг, и в освободившуюся первую

ячейку СР запишется второй проверочный бит r

n-k-2

= h

k-2

+ h

k-3

+ ... + h

k-1

n-k-1

. Чеpез

n-k тактов будут вычислены все n-k проверочных символов r

, r

, …, r

n-k-1

и записаны в

СР. После k тактов, т. е. после вывода на выход всех информационных символов,

станут выводиться проверочные символы в том же порядке, в каком они вычислялись.

На выходе получается блочный код. После k тактов процесс кодирования одной ком-

бинации А

(Х) заканчивается, и СР принимает исходное состояние. Для кодирования

следующей комбинации необходимо стереть А

(Х), ввести в СР новую А

(Х) и повто-

рить цикл из n тактов.

Рассмотрим более конкретно работу этой схемы на примере использования её в

качестве КУ с привязкой начальных условий к данным предыдущих примеров 1, 2 и 3.

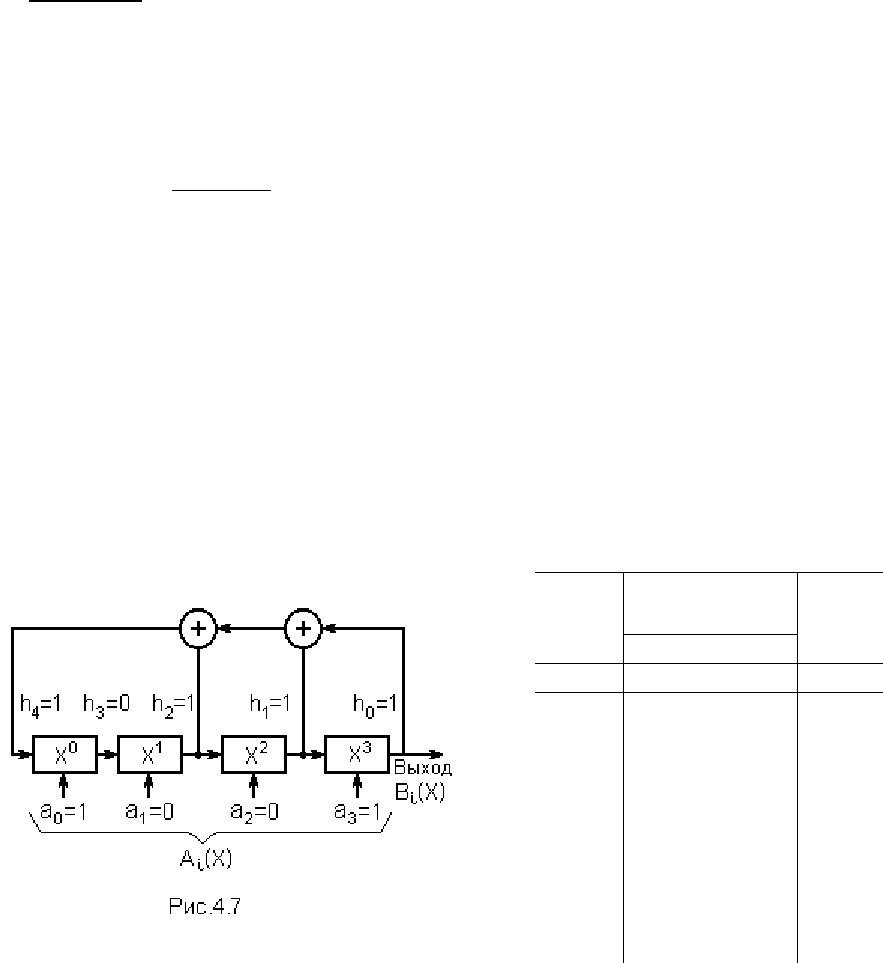
Пример 6. Построить схему КУ, обеспечивающего кодирование ЦК Хемминга (7,4)

с порождающим полиномом G(X) =1 + X + Х

путём вычисления блока проверочных сим-

волов "в целом", используя проверочный полином Н(Х). Проследить по тактам про-

цесс кодирования и состояние элементов схемы при кодировании исходной комбина-

ции 1001 ~ 1 + X

= A(X).

Построение схемы КУ определяется проверочным полиномом (4.34)

.XXX1

XX1

)X(H

+++=

Так как k = 4, то число разрядов СР равно четырём. По виду проверочного поли-

нома определяем, что h

= h

= 1, h

= 0.

Схема КУ для условий примера приведена на рис. 4.7. Состояние ячеек СР и

выхода схемы по тактам - в табл. 4.

В исходном положении в триггерные ячейки СР записываются информационные

символы A

(X) = 1 + X

~ 1001. Учитывая наличие обратной связи в СР с выхода на

вход, суммирование по модулю 2 выходов ячеек Х

, Х

и X

даст символ записи в ячей-

ку Х

. После первого сдвига в Х

будет записан символ проверочной группы r

, который

при последующих сдвигах продефилирует на выход СР. Из табл. 4 видно, что после

n=7 тактов на выходе образуется комбинация 0111001 (старшим разрядом вперед),

такая же, как в примерах 1 и 2.

Таблица 4.

Состояние

ячеек

Номер

такта

Выход

A(X) 1 0 0 1 --

1 1 0 0

1 1 1 0

0 1 1 1

1 0 1 1

0 1 0 1

0 0 1 0

1 0 0 1

При этом триггерные ячейки СР принимают исходное значение 1001, и при не-

обходимости возможно повторение процедуры кодирования этой же кодовой комби-

нации A

(X) путём подачи очередных следующих n =7 тактов. Таким образом, этот

способ кодирования так же, как и первый вариант схемы для деления полиномов, обес-

печивает получение кодовых комбинаций разделимого, блочного ЦК. Кроме того, по-

добная ЛПС может быть использована для генерации определённой кодовой комби-

нации, в частности, М - последовательности.

Рассмотрение вариантов построения ЛПС, выполняющих операции умножения и

деления полиномов, с целью использования в кодеках ЦК, позволяет сделать сле-

дующие выводы.

В КУ ЦК процедура умножения полиномов приводит к получению нераздели-

мых кодов, что усложняет их последующее декодирование. Поэтому операция умноже-

ния редко используется в устройствах формирования и обработки ЦК.

2) При делении на порождающий полином G(X) код на выходе КУ получается

разделимым и СР содержит r разрядов. Так как в большинстве случаев используют-

ся ЦК, у которых число проверочных символов r существенно меньше числа информа-

ционных (r<k), то СР в этом случае будет иметь меньшее число разрядов, чем при де-

лении на генераторный полином.

3) При делении в КУ исходной кодовой комбинации на генераторный многочлен

ЦК также получается разделимым, но в СР требуется использовать не r, а k разрядов,

которых, как правило, больше.

Применение этого способа более целесообразно в тех случаях, когда одна и та же

кодовая комбинация передаётся по каналу связи многократно, например, при передаче

формата сообщения с аварийных буев в системах поиска и спасения терпящих бедст-

вие объектов.

Линейные переключательные схемы широко применяются как при формировании

и обработке ЦК, так и при генерировании кодированных последовательностей, в част-

ности, М - последовательностей. Рассмотрим ряд характерных примеров применения

ЛПС в технике связи.

1.11. Кодирующее и декодирующее устройства для кода Хемминга (7,4)

Студенты уже знакомы с построением кодера и декодера для кода Хемминга

(7,4) по работе №3. Однако эти схемы строились с учётом "поэлементного" получения

символов проверочной группы и синдрома в соответствии с алгоритмом (4.14). Покажем,

как реализуются эти же схемы с учётом того, что коды Хемминга относятся и к классу

ЦК.

Кодер для кода Хемминга (7,4). Для построения КУ по классической схеме де-

ления (см. рис. 4.5), так как кодирование путём вычисления остатка "в целом" требует

предварительного выполнения операции умножения на оператор сдвига X

и сложе-

ния полинома-остатка с полиномом-произведением A

(X)·X

(4.15), требуется предва-

рительно видоизменить структуру схемы. Для выполнения операции умножения сле-

дует разместить сумматор, на который подключён вход, в конце СР, перед обратной

связью g

-1

. Такое подключение входа эквивалентно умножению на X

, так как исклю-

чается задержка на r ТИ.

Для выполнения операции сложения остатка R

(X) с полиномом A

(X)·X

(4.15) не-

обходимо выход КУ подключить к одному из входов схемы логического сложения (ИЛИ),

ко второму входу которой подключается вход схемы .для выдачи на выход без задержки

информационной кодовой комбинации A

(X) (старшим разрядом вперёд).

Подробнее рассмотрим работу схемы на конкретном примере,

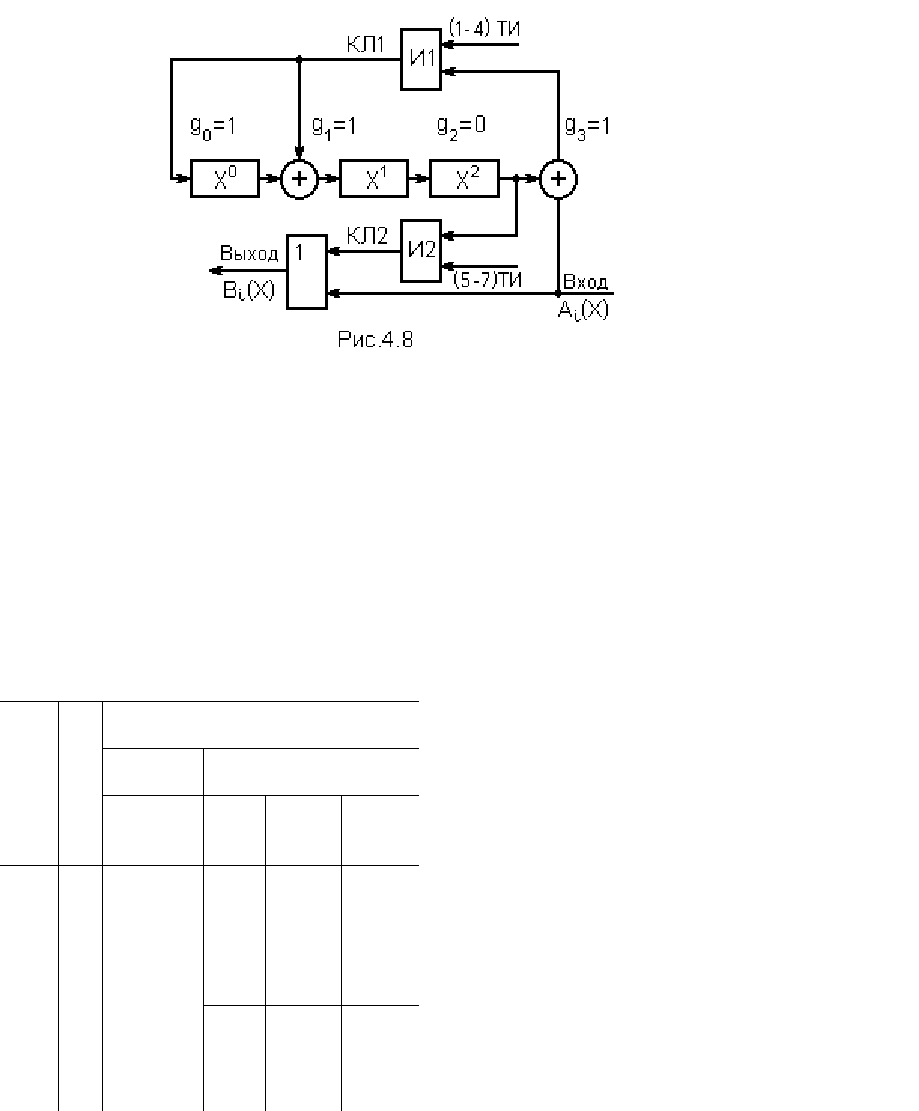
Пример 7. Построить схему КУ, обеспечивающего кодирование ЦК (7,4) с порож-

дающим полиномом G(X) = 1 + X + X

путём определения проверочной группы методом

деления полиномов и определения остатка R(X). Проследить по тактам процесс кодиро-

вания и состояние элементов схемы при кодировании исходного полинома A

(X) = 1+X

~ 1001.

Схема кодера для условий примера приведена на рис. 4.8, состояние ячеек СР и

выхода схемы по тактам — в табл. 5.

Наряду с вышеотмеченными особенностями построения схемы, КУ дополнено

двумя ключевыми схемами, роль которых выполняют схемы логического умножения И1

и И2, соответственно. В течение первых k = 4 тактов на второй вход схемы И1 посту-

пают ТИ, обеспечивая прохождение символов от выходного сумматора в шину обрат-

ной связи СР. Начиная с 5-го по 7-й такт, ТИ на второй вход схемы И1 не поступают, и

обратная связь разрывается. В это время поступают ТИ на второй вход схемы И2, бла-

годаря чему выход СР подключается к выходу всего КУ, обеспечивая выдачу остатка от

деления кодовой комбинации A

(X) на порождающий полином G(X) на выход, для

подстыковки проверочных символов к A

(X).

Таблица 5

Состояние

ячеек ключей

Номер

такта

Вход

Выход КЛ1 КЛ2

Замкнут Разом-

кнут

0 0 0

1 1 0

0 1 1

1 1 1

0 1 1

0 0 1

0 0 0

Разом-

кнут

Замкнут

Из табл.5 видно, что после 4-го такта в

СР образ

ется остаток 011, т.е.

(

)

=X+X

, а в течение n тактов на выход

пост

пает кодовая комбинация 0111001 ~

X + Х

+ Х

+ X

(

старшим разрядом впе-

ред) — см. пример 1.

Декодер для кода Хемминга (7, 4).

При аппаратурной реализации декодеров

ЦК для определения синдрома использу-

ют схему, осуществляющую процедур

деления полинома на полином (см. рис.

4.5). При построении ДУ следует допол-

нительно включать ЗУ на k элементов и

схему опроса остатка при делении.

Эта схема состоит из схемы логического сложения (ИЛИ) на r входов и схемы ло-

гического умножения (И) на два входа. СР и обратные связи должны соответство-

вать структуре порождающего полинома G(X), т. е. число ячеек СР должно быть

равным r, а замкнутая обратная связь должна соответствовать ненулевым коэф-

фициентам полинома G(X).

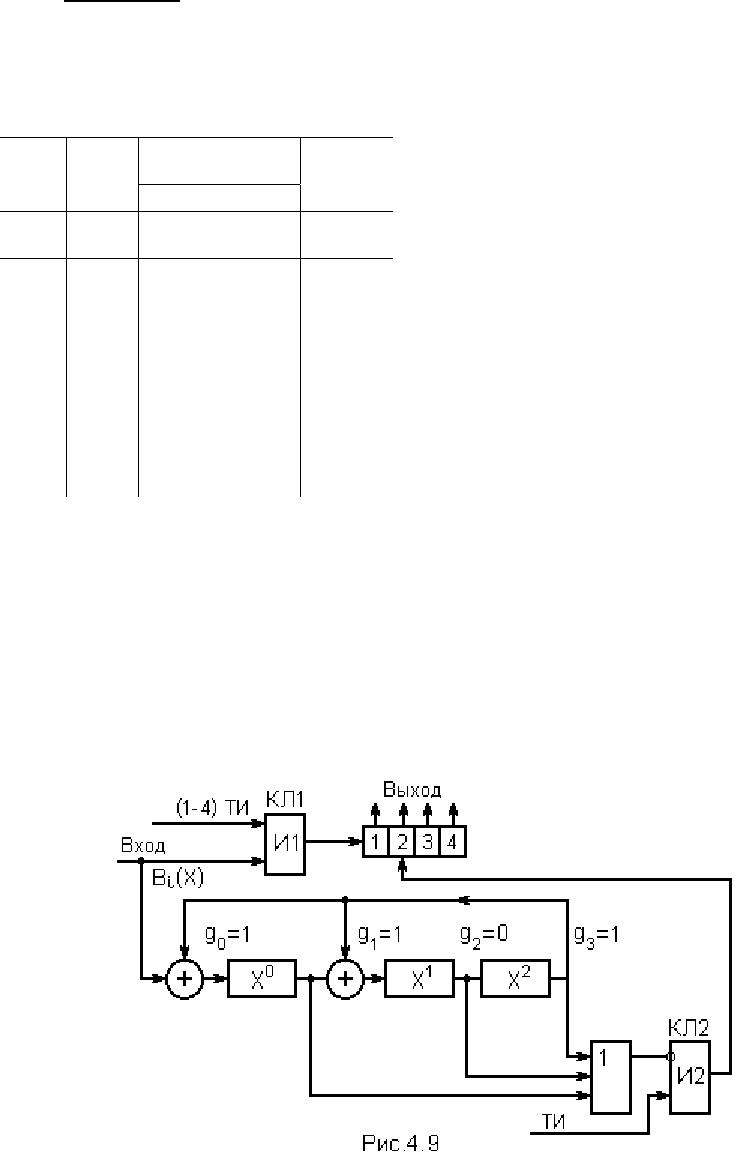
Пример 8. Построить схему ДУ для ЦК Хемминга (7, 4) с порождающим по-

линомом G(X) = 1 + X + X

и по тактам сдвигающих импульсов проследить за его

работой. Схема ДУ должна решать задачу обнаружения ошибок.

Таблица 6

Состояние

ячеек

Вход

B(X)

Номер

такта

Выход

СР

Исх.

сост.

0 0 0

1 0 0

0 1 0

0 0 1

0 1 0

1 0 1

0 0 0

На рис.9 приведена схема ДУ, в табл.6

представлены состояния ячеек СР при деко-

дировании входной кодовой комбинации

(X)=X + X

+ Х

~ 0111001, принимае-

мой без ошибок.

Декодирующее устройство работает сле-

дующим образом. Кодовая комбинация B

(X)

старшим разрядом вперёд поступает на СР

для определения остатка при делении и в ЗУ

на k элементов через открытую схему И1,

которая через k тактов закрывается, так как

прекращается подача из синхронизатора ТИ

на один из входов схемы И1.

При этом в ЗУ запоминаются k информационных символов принимаемой

кодовой комбинации B

(X).

В СР поступают все n элементов B

(X), и после n тактов происходит опрос

состояния ячеек СР путём подачи циклового импульса с синхронизатора на схему

И2. Если R(X) ≠ 0, то на выходе схемы И2 импульс не появится и считывания с ЗУ

принятых информационных символов не произойдет. Если R(X) = 0, то появив-

шийся на выходе И2 импульс считывает A

(X) на выход и выдаёт четыре инфор-

мационные бита получателю сообщений.

1.12. Принципы построения декодирующих устройств

для циклических кодов с исправлением ошибок

Декодирование принятых комбинаций ЦК можно производить различными

методами. Наряду с синдромным методом декодирования, основанным на вычис-

лении остатка от деления принятой комбинации на порождающий код полином,

существует целый ряд других методов, упрощающих процедуру декодирования и

не требующих хранения в памяти ДУ большого числа синдромов при обработке

длинных кодов. Для длинных ЦК разработаны специальные итеративные проце-

дуры декодирования с исправлением нескольких ошибок, например, метод Берле-

кэмпа или более совершенный итеративный алгоритм Тренча-Берлекэмпа-Месси

(ТБМ-метод), оперирующий с полиномами над полями Галуа. Различные методы

декодирования так же, как и коды, получают авторские наименования. Известны

алгоритмы декодирования Хемминга, Питерсона, Ченя, Мэггита, Витерби и других

[5—10]. В лабораторной работе "Циклические коды" используется синдромный

метод декодирования ввиду малой длины исследуемого БЧХ-кода.

Декодирующие устройства для кодов, предназначенных только для обнару-

жения ошибок, по существу, не отличаются от схем КУ (см. подраздел 1.11). В них

добавляется лишь буферный регистр для хранения принятого сообщения на вре-

мя проведения операции деления. Если остаток-синдром при делении оказыва-

ется нулевым, что свидетельствует об отсутствии ошибки, то информация с бу-

ферного регистра считывается в дешифратор сообщения ПС. Если остаток обна-

ружен, что свидетельствует о наличии ошибки, то информация в буферном реги-

стре уничтожается и на передающую сторону к ИС посылается импульс запроса

повторной передачи по обратному каналу связи.

В случае исправления ошибок схема ДУ, естественно, усложняется. Ин-

формацию о разрядах, в которых произошла ошибка, т. е. о виде шумового векто-

ра Z(X) (4.16), содержит, как и ранее, синдром, получаемый в результате деления

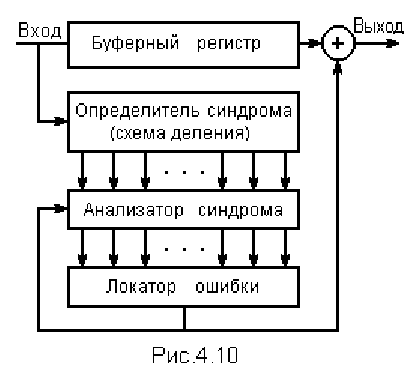
полиномов. Структурная схема ДУ, решающего задачу исправления ошибок,

представлена на рис. 4.10.

Символы подлежащей декодированию кодовой комбинации, возможно, со-

держащей ошибку, последовательно, начиная со старшего разряда, вводятся в

n-разрядный буферный регистр сдвига и одновременно в схему определителя

синдрома, где за n тактов деления определяется остаток, который в случае син-

хронной, непрерывной передачи кодовых комбинаций сразу же переписывается в

аналогичный СР схемы анализатора синдрома.

В состав схемы анализатора синдрома может входить ПЗУ, в котором записаны

все возможные конфигурации синдромов с соответствующими им шумовыми век-

торами. Кодовые комбинации шумовых векторов (4.16) содержат "единичные"

символы на тех позициях, которые в процессе передачи сообщения по каналу

связи оказались искажёнными помехами.

Локатор ошибок (определитель места ошибок) представляет собой ком-

бинаторно-логическую схему, выдающую на выход единичные символы в те мо-

менты времени, когда каждый из ошибочных символов принятой кодовой комби-

нации занимает в буферном регистре крайнюю правую ячейку. При последующем

тактовом сдвиге локатор ошибки (детектор ошибки) формирует символ "1", кото-

рый поступает на сумматор коррекции, представляющий собой схему суммирова-

ния по модулю 2, где исправляется искажённый символ.

Одновременно по цепи обратной связи с выхода локатора ошибки подаётся

единичный символ на анализатор синдрома, что в ряде конкретных схемных ре-

шений построения анализатора упрощает его построение на базе ЛПС без ис-

пользования ПЗУ [5]. Сложность анализатора синдрома и локатора ошибки зави-

сит от гарантированного числа исправляемых и обнаруживаемых ошибок. Естест-

венно, простейшие схемные решения получаются при обработке кодов, рассчи-

танных на исправление единичных ошибок.

Как видно из рассмотрения логики работы структурной схемы декодера (см.

рис. 4.10), наиболее сложной частью его является необходимость запоминания

заранее вычисленных синдромных полиномов и соответствующих им векторов

ошибок. Достоинством ЦК как раз и является то, что анализатор синдрома можно

значительно упростить, воспользовавшись алгебраической структурой кода для

отыскания связей между синдромами при числе исправляемых ошибок g

>1. Опи-

раясь на эти связи, можно запомнить в ПЗУ только полиномы ошибок, соответст-

вующие некоторым типичным синдромным полиномам, а вычисление остальных

осуществить затем с помощью простых вычислительных алгоритмов. Именно на

таких принципах работают различные варианты декодеров Мэггита [5,9].

2. ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ

Перед началом выполнения лабораторной работы " Циклические коды" сту-

дент должен получить у преподавателя номер порождающего полинома G(X) ЦК,

задаваемого в восьмеричной системе счисления (табл. 7), и информационное

слово в виде десятичного числа от 1 до 127.

Таблица 7

№

G(X)

№

G(X)

№

G(X)

№

G(X)

1 23 7 117 13 427 19 2041

2 31 8 135 14 673 20 2467

3 37 9 171 15 721 21 3545

4 41 10 213 16 1163 22 4657

5 53 11 321 17 1315 23 6143

6 65 12 347 18 1471 24 7531

Работа "Циклические коды" выполняется на персональных ЭВМ, в среде

операционной системы MS-DOS. Для выполнения лабораторной работы (ЛР №4)

необходимо выбрать соответствующую позицию меню и нажать клавишу

<ENTER>. После небольшой паузы на экране дисплея появится заголовок

"Часть1" и приглашение ввести порождающий полином. В случае ввода ошибоч-

ных символов выдаётся сообщение "Ошибка ввода, повторите", после чего необ-

ходимо заново ввести строку, в которой была допущена ошибка.

Для прекращения выполнения лабораторной работы достаточно в любой

момент нажать клавишу < ESС>.

Программа выполнения работы включает четыре части.