Никитин Г.И. Помехоустойчивые циклические коды
Подождите немного. Документ загружается.


11
5. Как было показано на примере в подразделе 1.2, умножение полинома на X при-
водит к сдвигу членов полинома на один разряд влево, а при умножении на X
r
, соответ-
ственно, на r разрядов влево, с заменой r младших разрядов полинома "нулями". Умно-
жение полинома на X свидетельствует о том, что при этой процедуре X является "опера-
тором сдвига". Деление полинома на X приводит к соответствующему сдвигу членов по-
линома вправо с уменьшением показателей членов на 1. Процедура сдвига позволяет к
исходной кодовой комбинации А
i
(Х), после домножения её на X
r
, дописать справа r про-
верочных символов.
6. Поскольку разрешённые кодовые слова ЦК B
i
(X) без остатка делятся
на порождающий полином G(X) с получением итога в виде информационной комбинации
А
i
(Х) (4.1), то имеется возможность формировать B
i
(X) на стороне передачи (кодирующее
устройство) простым методом умножения (4.2).
Два последних свойства ЦК позволяют осуществить построение кодеров ЦК двумя
методами: методом умножения и методом деления полиномов. Рассмотрим достоинства
и недостатки этих методов с учётом вариантов построения декодеров ЦК, соответствую-
щих этим методам.
Метод умножения позволяет при формировании разрешённых кодовых комбина-
ций по алгоритму (4.2) использовать любой порождающий полином, лишь бы его макси-
мальная степень была равна числу необходимых проверочных символов r.
Однако этот метод обладает двумя существенными недостатками.
Во-первых, при формировании ЦК методом умножения в полученной комбинации
B
i
(X) в явном виде не содержатся информационные символы. Код получается неразде-
лимым с "перетасованными" информативными и проверочными символами, что затруд-
няет его декодирование, так как это приводит к необходимости применять метод макси-
мального правдоподобия в декодирующем устройстве (ДУ).
Метод максимального правдоподобия (ММП) предполагает при исправлении
ошибок принимаемую кодовую комбинацию отождествлять с той разрешённой, к которой
принятая находится ближе всего. При таком непосредственном способе декодирования в
памяти запоминающего устройства (ЗУ) декодера необходимо хранить все разрешённые
кодовые комбинации N
0
, что требует на стороне приёма больших объёмов ЗУ и большого
времени обработки при декодировании. Эти обстоятельства являются вторым недостат-
ком метода умножения при кодировании ЦК.
Исследования показывают [5 - 8], что хороший циклический корректирующий код с
кратностью исправляемых ошибок g
u
≥ 5 при относительной скорости кода В
к
≥ 0,5, т. е.
коэффициенте избыточности к ≤ 0,5, должен иметь число информационных символов
k ≥ 40 . Это значение и приводит к техническим трудностям при процедуре декодирова-
ния по ММП, сводящейся к сравнению принятой кодовой комбинации со всеми N
0
раз-
решёнными.
Для примера определим время декодирования Т
дк
принятой кодовой комбина-
ции, если число информационных символов в ней k= 40 и для сравнения использует-
ся ЭВМ со скоростью 10
7
операций в секунду. Будем полагать, что для сравнения при-
нятой кодовой комбинации с одной из разрешённых достаточно одной операции на
ЭВМ. Тогда для проведения N
0
= 2
k
= 2
40
сравнений потребуется время декодирования
ч.
ЭВМ
к
Д
30
3600
5
1011
1011
10
1011
10
2
5
7
12
7
40
0
=
⋅
=⋅=
⋅
===
c
,
c,
,
V
N
T
Как видно из примера, задача декодирования простым перебором и сравнением
непосильна даже для современных ЭВМ.
В соответствии с этим, основным направлением в теории кодирования является
поиск таких кодов и алгоритмов их формирования и обработки, для которых не требуется
хранение в ЗУ разрешённых кодовых комбинаций. Эти задачи решаются, в частности,

12
при построении кодеров на основе деления полиномов, а при декодировании — на ос-
нове синдромного метода декодирования (СМД).
Метод деления полиномов позволяет представить разрешённые к передаче
кодовые комбинации в виде разделённых информационных A
i
(X) и проверочных
R
i
(X)
символов, т. е. получить блочный код.
Поскольку число проверочных символов равно r, то для компактной их записи в
последние младшие разряды кодового слова надо предварительно к A
i
(X) справа при-
писать r "нулей", что эквивалентно умножению A
i
(X) на оператор сдвига X
r
(см. свой-
ство 5 ЦК).
На практике предпочитают использование метода деления полиномов при по-
строении кодеков, поскольку при этом имеется возможность представить кодовую
комбинацию в виде разделённых информационных и проверочных символов:
B
i
(X) = A
i
(X) ·X
r
+ R
i
(X), (4.15)
где R
i
(X) — остаток от деления A
i
(X) ·X
r
/G(X).
В алгоритме (4.15) можно выделить три этапа формирования разрешённых ко-
довых комбинаций в кодирующем устройстве:
1) к комбинации первичного кода A
i
(X) дописывается справа r нулей,
что эквивалентно умножению A
i
(X) на X
r
;
2) произведение A
i
(X)·X
r
делится на соответствующий порождающий
полином G(X) и определяется остаток R
i
(X), степень которого не превышает r - 1, этот ос-
таток и даёт группу проверочных символов;
3) вычисленный остаток присоединяется справа к A
i
(X) ·X
r
.
Пример 1. Рассмотрим процедуру кодирования по алгоритму (4.15): для кодо-
вой комбинации А=1001 сформировать кодовую комбинацию циклического кода (7,4).
В заданном ЦК n = 7, k = 4, r = 3, и из табл. 1 выберем порождающий полином
G(X) = X
3
+ X + 1 (код Хемминга). Выполним три необходимые операции для получения
кодовой комбинации ЦК согласно алгоритму (4.15):
A
i
(X) = 1001 ~ X
3
+ 1 , ( знак " ~ " – тильда – означает соответствие).
1. A
i
(X) ·X
r
= (X
3
+ 1 ) · X
3
= X
6
+ X
3
~1001000, ( n =7).
2. A
i
(X) ·X
r
/G(X) = X
6
+ X
3
│
X
3
+ X + 1
+ │——————
X
6
+ X
4
+ X
3
X
3
+ X
——————
X
4
+
X
4
+ X
2
+ X
——————
X
2
+ X - остаток R
i
(X) = X
2
+ X ~ 110.
3. B
i
(X) = A
i
(X) ·X
r
+ R
i
(X) = 1001110 - итоговая комбинация ЦК.
Синдромный метод декодирования (СМД) предполагает в ДУ принятую кодовую
комбинацию поделить на порождающий полином. Если принятая комбинация являет-
ся разрешённой, т. е. не искажена помехами в канале связи, то остаток от деления бу-
дет нулевым. Ненулевой остаток свидетельствует о наличии в принятой кодовой ком-
бинации ошибок, остаток от деления и называется синдромом.
Термин "синдром" заимствован из медицинской практики (от греч. вместе бе-
гущий) и означает сочетание (комплекс) симптомов болезни, характерное для опреде-
лённого заболевания. В теории кодирования синдром, который также называют опозна-
вателем ошибки, обозначает совокупность признаков, характерных для определённой
ошибки. Для исправления ошибки на стороне приёма необходимо знать не только факт

13
её существования, но и её местонахождение, которое определяется по установленно-
му виду вектора ошибки z(X).
После передачи по каналу с помехами принимается кодовое слово
B
i
' (X) = B
i
(X) + z(X), (4.16)
где B
i
(X) - передаваемая кодовая комбинация; z(X) — полином (вектор) ошибки,
имеющий степень от 1 до n -1.
При декодировании принятое кодовое слово делится на G(X)
,)X(S)X(U
)X(G
)X(B
ii
i
+=
′
(4.17)
где остаток от деления S
i
(X) и является синдромом.
Если при делении получается нулевой остаток S
i
(X) = 0, то выносится решение
об отсутствии ошибки z(X) = 0. Если остаток (синдром) ненулевой S
i
(X)≠ 0, то выносится
решение о наличии ошибки и определяется шумовой вектор (полином) z(X), а затем -
передаваемое кодовое слово, поскольку из (4.16) следует
B
i
(X) = B
i
' (X) + z(X). (4.18)
Всякому ненулевому синдрому соответствует определённое расположение (кон-
фигурация) ошибок. Взаимосвязь между видом синдрома и местоположением оши-
бочного символа находится довольно просто. Достаточно в любую разрешённую кодо-
вую комбинацию ввести ошибку и выполнить деление на G(X). Полученный остаток
(4.17) - синдром и будет указывать на ошибку в этом символе.
В качестве примера для ЦК Хемминга (7,4), позволяющего исправлять одно-
кратную ошибку при d
min
= 3 (см. табл. 1), взаимосвязь между синдромом и ошибочным
символом для двух возможных порождающих полиномов кода (7,4) приведена в табл. 2.
Пользуясь этой таблицей, можно найти местоположение ошибки и исправить её.
Для параметров рассмотренного ранее примера 1, где была показана процедура
кодирования кодовой комбинации A
i
= 1001 при использовании порождающего полинома
G(X) = X
3
+ X +1 для кода Хемминга (7,4), исправляющего однократную ошибку, приве-
дём в примере 2 процедуру декодирования принятой с помехой кодовой комбинации.
Пример 2. Принятая кодовая комбинация ЦК (7,4) имеет вид
B
i
'(X)=1011110. Определить и исправить ошибку в B
i
' (X), если она имеется.
Выполним три необходимые операции, проводимые при декодировании:
Таблица 2
№ символа
комбинации со
старшего раз
-
ряда
Ошибочный сим
-
вол полинома
комбинации
Синдром для
порождающего
полинома
G(X)=X
3
+X+1
Синдром
для
порождающего
полинома
G(X)=X
3
+X
2
+1
Шумовой
вектор
z(X)
7
6
5
4
3
2
1
X
6
X
5
X
4
X
3
X
2
X
1
X
0
)4,7(H
001
010
100
011
110
111
101
к
=
см. 4.29
)4,7(H
~
001
010
100
101
111
011
110
к
=
см. 4.29
1000000
0100000
0010000
0001000
0000100
0000010
0000001
Нет ошибки
000 000
0000000
1) в соответствии с алгоритмом (4.17) производим деление

14
B
i
' (X) / G(X) = X
6
+ X
4
+ X
3
+ X
2
+ X │ X
3
+ X +1
│——————
X
6
+ X
4
+ X
3
X
3
—————————
X
2
+ X - остаток R(X) = X
2
+ X ~ 110,
отметим, что совпадение остатков в примере 1 и 2 — чисто случайное, в примере 1
остаток являлся проверочной группой кода, а в примере 2 - синдромом;
2) по полученному синдрому 110 в соответствующем опознавателе синдрома (де-
шифраторе синдрома, локаторе ошибки) определяем вид шумового вектора
z(X) 0010000 (см. табл. 2);
3) воспользовавшись алгоритмом (4.18), исправляем принятую кодовую
комбинацию B
i
' (X) и получаем переданную комбинацию B
i
(X):
B
i
(X) = B
i
' (X) + z(X) = 1011110
+
0010000
————
1001110 – исправленная комбинация на выходе
ДУ с инвертированием неверно принятого символа.
Число проверочных символов r = n - k определяет число исправляемых ошибок.
Значение r должно быть достаточным для получения необходимого числа синдро-
мов S
Σ
(опознавателей ошибок). Так, для исправления всех одиночных (однократных)
ошибок необходимо S
Σ
= n +1 синдромов, так как шумовой вектор может принимать сле-
дующие n значений:
000...01, 000...10, ..., 001...00, 010...00, 100...00,
кроме того, необходим один синдром для определения факта безошибочного приёма ко-
довой комбинации S
0
= 000...00. Таким образом, для двоичных кодов при необходимо-
сти исправления всех однократных ошибок требуется выполнение соотношения
S
Σ
= 2
n – k
= 2
r
= n +1 , (4.19)
поскольку синдром формируется на месте r проверочных разрядов кода.
Плотноупакованные коды — такое название получили коды, у которых соблюда-
ется точное равенство
В
(4.19) числа необходимых синдромов для исправления ошибок
заданной кратности. Вследствие уникальности таких кодов, плотноупакованные коды
называют также "совершенными" или "оптимальными". К таким кодам относятся коды
Хемминга, которые при минимальном кодовом расстоянии d
min
= 3 обеспечивают ис-
правление всех однократных ошибок, поскольку у классических кодов Хемминга число
символов n = 2
r
-1 удовлетворяет условию (4.19).
В общем случае, при необходимости исправления всех независимых ошибок крат-
ности до g
и
включительно, требуемое число синдромов определяется выражением
,CC...CCCS
g
i
i
n
g
nnnn
∑
=
Σ
=+++++=
и
и
0
321
1
(4.20)
где
!)!(
!
iin
n
C
i
n
⋅−
= - число сочетаний из n по i, причём 1C
0
n
=
, так как 0! = 1.
С учётом (4.19) и (4.20), можно получить выражение для оценки числа про-
верочных символов r при необходимости исправления g
и
- кратных ошибок в принятых
кодовых комбинациях
.Clogr
g
i
i
n
≥
∑
=
и
0
2
(4.21)
15
Занимаясь поиском плотноупакованных кодов ("кодов без потерь"), М. Голей заме-
тил (опубликовано в 1949 году), что
,CCCC
113
23
2
23
1
23
0
23
21771253231 =+++=+++
а это означало, что может существовать плотноупакованный двоичный (23,12) код,
удовлетворяющий условию (4.20), исправляющий все кодовые комбинации с тремя
или менее ошибками. Он показал, что такой код действительно существует и в даль-
нейшем этот код получил его имя.
Код Голея относится к классу ЦК с порождающими двойственными (дуальными)
полиномами (4.9):
.XXXXXX)X(G
~
;XXXXXX)X(G
1
1
567911
24561011
++++++=
++++++=
(4.22)
Простым вычислением проверяется, что
,)X(G
~
)X(G)1X(1X
23
⋅⋅+=+
в связи с чем в качестве порождающего полинома ЦК Голея (23, 12) можно использо-
вать как G(X), так и G̃(X).
Код Голея, гарантированно исправляющий ошибки с кратностью не менее трёх
включительно, обладает минимальным кодовым расстоянием, d
min
=2g
и
+1 = 7, что, как
правило, указывается в маркировке кода (23, 12, 7). Добавление к этому коду общей
проверки на чётность по всем позициям увеличивает на единицу как общую длину кода,
так и минимальное кодовое расстояние d
min
= 8.
Расширенный код Голея, имеющий маркировку (24, 12, 8), состоит из 12 ин-
формационных символов и 12 проверочных, т. е. представляет собой код, обладающий
скоростью 1/2 и избыточностью, также равной 1/2.
Обратим внимание на то, что плотноупакованные коды Хемминга и Голея — цик-
лические, которые принадлежат классу двоичных линейных кодов. Общим для линей-
ных двоичных кодов является наличие, в качестве разрешённого, нулевого кодового
слова 000...00, что приводит к тому, что минимальный вес w
min
ненулевого разрешённо-
го кодового слова равен минимальному кодовому расстоянию d
min
(4.13).
В общем случае вес кодовых комбинаций может принимать различные значения,
и совокупность чисел кодовых комбинаций с постоянным весом N
w
определяют как рас-
пределение весов кода или как спектр весов кода. Распределение весов в коде Голея
(23, 12, 7) следующее:
N
0
= N
23
= 1; N
7
= N
16
= 253; N
8
= N
15
= 506; N
11
= N
12
= 1288,
а в расширенном коде Голея -
N
0
= N
24
= 1; N
8
= N
16
= 759; N
12
= 2576. (4.23)
Кодовые слова с весом 12, 8 и 16, выделенные из кода (24,12,8). образуют КПВ
максимальной мощности.
К сожалению, кроме кодов Хемминга (d
min
= 3, g
и
=1) и кода Голея (23, 12, 7)
пока не найдено других совершенных, плотноупакованных кодов, число синдромов у
которых точно соответствует требуемому значению для гарантированного исправления
ошибок заданной кратности.
1.5. Построение порождающих и проверочных матриц циклических кодов
Наряду с полиномиальным способом задания кода, структуру построения кода
можно определить с помощью матричного представления. При этом в ряде случаев
проще реализуется построение кодирующих и декодирующих устройств ЦК.

16
Рассмотрим варианты формирования и обработки ЦК, заданных в виде порож-
дающих и проверочных матриц, на конкретном примере ЦК Хемминга (7, 4), восполь-
зовавшись выражением (4.11), в котором определены двойственные (дуальные) поро-
ждающие полиномы кода:
X
7
+1 = (X +1) (X
3
+X+1) (X
3
+X
2
+1),
что соответствует кодам (7, 6); (7, 4); (7, 4),
Пример 3. Задан ЦК (7,4) дуальными порождающими полиномами
G(7,4) = X
3
+X+1 и .1XX
23
++=),(
~
47G
Составить порождающие матрицы для формирования разрешённых кодовых
комбинаций и проверочные матрицы для получения синдромов.
Первой строкой в матрице записывается порождающий полином (в двоичном
представлении) с домножением его на оператор сдвига X
r
для резервирования места
под запись r = 3 проверочных символов. Следующие k - 1 строк матриц получаются путём
последовательного циклического сдвига базового кодового слова матрицы G и G
~
на од-
ну позицию вправо, поскольку при этом по определению ЦК также получаются разре-
шённые к передаче кодовые комбинации:
0001011
0010110
0101100
1011000
47
=
),(G
1
2
3
4
0001101
0011010
0110100
1101000
47
=
),(G
~
1
2
3
4
(4.24)
Однако в таком виде эти порождающие матрицы размерностью k×n -(n столбцов,
k строк) могут образовать только неразделимый ЦК, т. е. код, у которого не определены
жёстко места информационных и проверочных элементов. Для построения порождаю-
щей матрицы, формирующей разделимый блочный код, необходимо матрицу преобра-
зовать к каноническому виду путём простых линейных операций над строками, промар-
кированными № 1- 4.
С учётом свойства ЦК (4.12), каноническую форму матрицы можно получить пу-
тём сложения ряда разрешённых кодовых комбинаций. Каноническая матрица должна
в левой части порождающей ЦК матрицы содержать единичную диагональную квад-
ратную подматрицу порядка " k " для получения в итоге блочного ЦК. С этой целью для
получения первой строки канонической матрицы G
K
(7,4) необходимо сложить по моду-
лю 2 строки с номерами 1, 3 и 4 матрицы G(7, 4), а для матрицы ),(
~
47G
k
— строки с
номерами 1, 2 и 3 матрицы ),(
~
47G . В этом случае в матрицах (4.24) в первых строках ос-
таются "1" только на первых позициях, а остальные "k-1" символов заменяются "0", что и
соответствует первым строкам единичных подматриц порядка "k". Нормирование по-
следующих трёх строк канонических матриц производится путём соответствующего
суммирования строк матриц (4.24).
В итоге имеем следующий вид дуальных канонических матриц:
{
0110001
1100010
1110100
1011000
47
|
|
|
|
),(G
E
k
=
43421
),(G 47
44
33
422
4311
строк№
=
=
⊕=
⊕⊕=
{
1010001
1110010
0110100
1101000
47
|
|
|
|
),(G
~
E
k
=
43421
),(G
~
47
44
433
4322
3211
строк№
=
⊕=
⊕⊕=
⊕⊕=
(4.25)
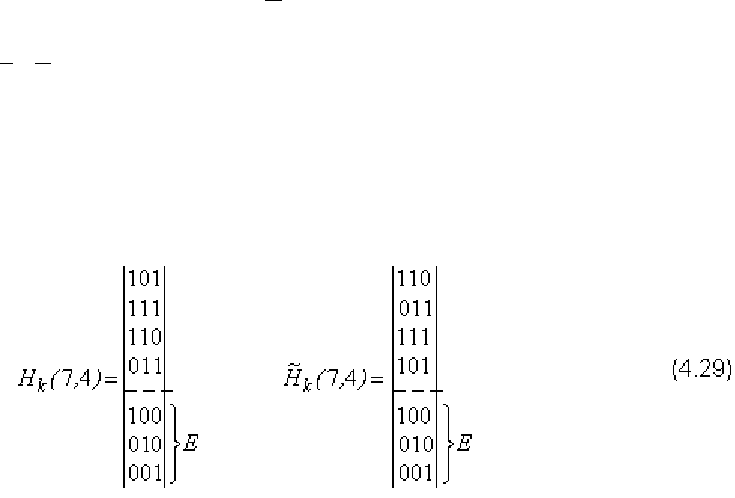
17
Процесс кодирования первичных кодов на стороне источника сообщений
сводится к умножению информационных посылок, представленных в виде векто-
ров Ā
i
(X), на соответствующую порождающую каноническую матрицу:
B
i
(X) = Ā
i
(X) ·G
k
. (4.26)
Эта процедура позволяет получить блочные коды Хемминга "в целом", т, е.
получить проверочную группу символов r
1
, r
2
, r
3
сразу после выполнения операции
(4.26). Наряду с этим имеется возможность формировать символы проверочной
группы поэлементно, как это предусматривалось при выполнении студентами ла-
бораторной работы № 3 "Корректирующие коды" [3], где 3 проверочных символа
задавались следующими равенствами проверки на чётность:
r
1
= i
1
⊕ i
2
⊕ i
3
;r
1
= i
1
⊕ i
3
⊕ i
4
;
r
2
= i
2
⊕ i
3
⊕ i
4
;r
2
= i
1
⊕ i
2
⊕ i
3
; (4.27)
r
3
= i
1
⊕ i
2
⊕ i
4
;r
3
= i
2
⊕ i
3
⊕ i
4
.
Обратим внимание на то, что алгоритм (4.27) просто получается из рассмотрения
порождающих коды Хемминга матриц (4.25), в которых проверочные подматрицы, содер-
жащие 3 столбца (r
1
, r
2
, r
3
), имеют символы " 1" в тех строках, номера которых совпадают с
маркировкой информационных символов i в равенствах (4.27) (см. (4.14)).
При матричном варианте обработки принятых кодов на стороне получателя
сообщений для получения синдрома необходимо принятую, возможно искажён-
ную в канале, кодовую комбинацию )( XB
i
′
умножить на проверочную матрицу
Н(Х):
.)X(H)X(BS
i
⋅
′
= (4.28)
Процедура построения проверочной матрицы Н достаточно подробно рас-
смотрена в [3]. Заметим, что матрица Н с размерностью n х r может быть полу-
чена из порождающей матрицы канонического вида (4.25) путём дополнения про-
верочной подматрицы единичной матрицей размерности r х r, что даёт следую-
щий вид дуальных проверочных матриц:
По определённому с помощью полученного синдрома (4.28) соответству-
ющему шумовому вектору исправляются ошибки (4.18).
Интересно отметить, что в табл. 2, в которой рассмотрена связь между син-
дромом и шумовым вектором для кода (7,4), колонки с синдромами дуальных по-
рождающих полиномов полностью совпадают с (4.29).
В ЦК Хемминга (n , k) все проверочные r = n - k разряды размещаются в
конце кодовой комбинации и, как отмечалось, формируются "в целом". При по-
элементном получении проверочных символов (4.27) целесообразно, чтобы каж-
дый синдром представлял собой двоичное число, указывающее на номер разря-
да, в котором произошла ошибка. Коды, в которых синдромы (опознаватели) со-
ответствуют указанному принципу, и предложил впервые Хемминг. В этом случае

18
для кода (7, 4) проверочные символы r
1
, r
2
, r
3
, (табл. 2) размещаются на первой,
второй и четвертой позициях кодовой комбинации, отсчитываемых справа налево.
Такое построение кодов упрощает декодирующее устройство на стороне получа-
теля сообщений.
1.6. Укороченные циклические коды
Поскольку ЦК порождаются делителями бинома Х
n
+1 (4.3), то для большей
части значений n и k имеется относительно мало кодов, удовлетворяющих всем свой-
ствам, присущим ЦК (см. подразд. 1.4). Поэтому естественно попытаться найти среди
линейных кодов такие, которые хотя и не являются в действительности циклическими,
обладают похожей математической структурой и столь же легко реализуются.
При разработке систем передачи информации, работающих с дискретными сиг-
налами в предположении необходимости исправления (обнаружения) ошибок, число
информативных символов k
Σ
выбирают, как правило, таким, чтобы оно было кратным
длине первичного кода k
1
:
k
Σ
= а k
1
, где а = 1, 2, 3, 4, …,
а значение n
Σ
= k
Σ
+ r, где число проверочных символов должно удовлетворять задан-
ному значению кратности обнаруживаемых и исправляемых ошибок. В частности, ЭВМ
обычно обмениваются машинными словами в виде байтов, состоящих из восьми сим-
волов (k
1
= 8).
При этом n
Σ
и k
Σ
часто не совпадают с табулированными в [6] ЦК. В этом слу-
чае по таблицам [6] находят ЦК, который соответствует обоснованному значению
r=n-k для классического, табулированного ЦК, а затем уменьшают n и k
Σ
до n-ℓ и
k
Σ
=k-ℓ, получая укороченный ЦК.
Укороченные циклические коды (УЦК) получают из полных ЦК, используя для пе-
редачи информации только кодовые комбинации полного кода, содержащие слева ℓ
нулей. Это даёт возможность построить УЦК (n-ℓ, k-ℓ) путём исключения первых ℓ
столбцов и ℓ строк из порождающей матрицы (4.24). Полученный код не будет строго
циклическим, так как циклический сдвиг не всегда будет приводить к получению оче-
редной разрешённой кодовой комбинации. Поэтому укороченные (усечённые) ЦК
часто называют псевдоциклическими или квазициклическими.
Укороченные ЦК сохраняют основные свойства классических ЦК (см. подраздел
1.4), к числу которых относятся следующие:
1) УЦК образуются делителями бинома Х
n
+1 - порождающими полиномами
G(X), такими же, как у полных ЦК;
2) УЦК относятся к классу линейных (групповых) кодов, для которых сумма раз-
решённых кодовых комбинаций УЦК также является разрешённой кодовой комбина-
цией (4.12);
3) УЦК обладает таким же минимальным (конструктивным) кодовым расстоя-
нием как у исходного ЦК, и таким же числом проверочных символов (4.21), но не мо-
жет быть плотноупакованным;
4) УЦК исправляет такое же число ошибок, что и ЦК, т.е. имеет такую же крат-
ность обнаруживаемых и исправляемых ошибок;
5) при построении кодеков УЦК используются те же схемы, что и для классиче-
ских ЦК, при условии, что каждому усечённому коду спереди приписывается ℓ нулей.
Специфику построения УЦК рассмотрим на следующем примере.
Пример 4. Передаче подлежит сообщение, закодированное стандартным
кодом МТК-2 с числом информационных символов k = 5. Обеспечить у получателя
сообщений исправление однократной ошибки в кодовом слове.
Однократная ошибка исправляется при минимальном кодовом расстоянии
d
min
=3. Этому значению удовлетворяют коды Хемминга (7,4), (15,11), (31,26) ... (см.
табл.1). Код (7,4) с числом информационных символов k= 4 не удовлетворяет ус-

19
ловию примера при необходимости передачи k = 5. Этому условию удовлетворяет
следующий по порядку код Хемминга (15,11), если из общего числа символов
n=15 и числа информативных символов k =11 вычесть одно и то же число ℓ= 6 (ис-
ключение первых ℓ столбцов и ℓ строк порождающей код матрицы с размерностью
k × n). Получаем УЦК (9, 5), удовлетворяющий условию примера k = 5, d
min
= 3, с
числом проверочных символов r = 4.
Для опорного ЦК (15,11) бином X
n
+1 раскладывается на следующие неприво-
димые полиномы:
X
15
+ 1 = (X + 1)·(X
2
+ X + 1) ·(X
4
+ X + 1) ·(X
4
+ X
3
+ 1) ·( X
4
+ X
3
+ X
2
+ X + 1),
из которых для построения кода r = 4 можно выбрать любой из трёх последних. Выберем
в качестве порождающего полинома G(X) = X
4
+ X+1 и на основе матрицы этого ЦК
(15,11) покажем, как осуществляется отсечка:
1
2
3
ℓ =
6
4
5
———
6
11
10
9
8
7
Усечённая
матрица
(9,5)
000010011
011000010
110000100
010011000
000010011
59 =),(G
1
2
3 (4.30)
4
5
Приведём усечённую матрицу G(9,5) к каноническому виду путём соот-
ветствующего суммирования строк по аналогии с проводимыми преобразованиями с
матрицами (4.24) и (4.25) и получим соответствующие равенства проверки на чёт-
ность при поэлементном формировании усечённого кода (9, 5) (см. (4.27) в качестве
аналога):
001100001
011000010
110000100
101101000
010110000
59
|
|
|
|
|
),(G
E
k
321
=
1 = 1⊕ 4⊕ 5
2 = 2 ⊕ 5
3 = 3
4 = 4
5 = 5
r
1
= i
2
⊕ i
3
;
r
2
= i
1
⊕ i
3
⊕ i
4
;
r
3
= i
2
⊕ i
4
⊕ i
5
;
r
4
= i
1
⊕ i
2
⊕ i
5
.
(4.31)
Обратим внимание на то, что порождающая матрица УЦК G
K
(9, 5) и соответст-
вующие ей алгоритмы проверки на чётность (4.31) полностью совпадают с выражениями
(3.22) методических указаний, по которым студентами выполнялась лабораторная рабо-
та № 3. Таким образом, УЦК (9, 5) полностью удовлетворяет условиям примера 4.
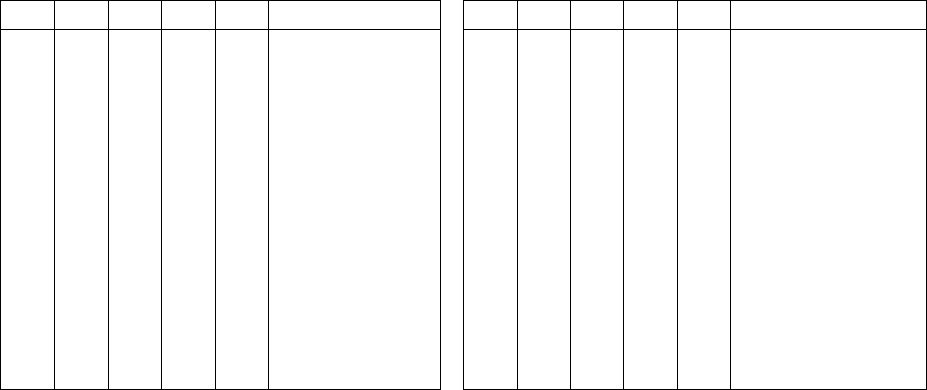
20
1.7. Циклические коды Боуза –Чоудхури –Хоквингема
Коды Боуза – Чоудхури - Хоквингема (БЧХ) представляют собой обширный класс
кодов, способных исправлять несколько ошибок и занимающих заметное место в тео-
рии и практике кодирования. Интерес к кодам БЧХ определяется по меньшей мере
тремя следующими обстоятельствами:
1) среди кодов БЧХ при небольших длинах существуют хорошие (но, как
правило, не лучшие из известных) коды;
2) известны относительно простые и конструктивные методы их кодирования и
декодирования;
3) полное понимание построения кодов БЧХ является наилучшей отправной
точкой для изучения многих других классов кодов.
Коды БЧХ независимо открыли Хоквингем (1959) и Боуз и Рой-Чоудхури (1960),
которые доказали ряд теорем, устанавливающих существование таких ЦК, у которых
минимизируется число проверочных символов, а также указывающих пути нахождения
порождающих полиномов для этих кодов.
Корректирующие свойства ЦК могут быть определены на основании следую-
щей теоремы: для любых значений m и g
и
существует ЦК длиной n = 2
m
-1, исправ-
ляющий все ошибки кратности g
и
и менее (g
и
< m) и содержащий не более n – k ≤ mg
и
проверочных символов. Так, например, при n = 15, m= 4 и различных g
и
число прове-
рочных символов будет равно: g
и
=1, n – k = m·g
и
= 4·1= 4; g
и
= 2, m·g
и
= 4·2 = 8; g
и
= 3,
m·g
и
= 4·3 = 12. Соответствующие коды (n, k) будут (15,11), (15,7), (15,3). Напомним, что
минимальное кодовое расстояние d
min
= 2 · g
и
+1 и применительно к ЦК оно чаще называ-
ется конструктивным расстоянием. Если величины g
и
или d выбрать слишком больши-
ми, то получившийся в результате код будет тривиальным — в нём будет лишь один ли-
бо (при r > n) ни одного информационного символа.
В табл. 3 даны параметры и порождающие полиномы некоторых кодов БЧХ. По-
линомы приведены в восьмеричной форме записи, старшая степень расположена слева.
Например, коду (15, 7) соответствуют двоичное представление 111010001 и мно-
гочлен G(X) = X
8
+ Х
7
+ Х
6
+ X
4
+1. Подробные таблицы порождающих полиномов цик-
лических кодов БЧХ приведены в [6].
Таблица 3
mn k rg
и
G(X) – mod 8 m n k r g
и
G(X) – mod 8
3
4
5
6
7
15
31
63
4
11
7
26
21
16
11
57
51
45
39
36
3
4
8
5
10
15
20
6
12
18
24
27
1
1
2
1
2
3
5
1
2
3
4
5
13
23
721
45
3551
107657
5423325
103
12471
1701317
166623567
1033500423
7
8
127
255
120
113
106
99
92
247
239
231
223
215
7
14
21
28
35
8
16
24
32
40
1
2
3
4
5
1
2
3
4
5
211
41567
11554743
3447023271
624730022327
435
267543
156720665
75626641375
23157564726421
Коды БЧХ с длиной 2
m
-1 называют примитивными кодами БЧХ. К ним, в част-
ности, относятся классические коды Хемминга, исправляющие однократные ошибки. К
кодам БЧХ относятся также коды, длина n которых является делителем 2
m
-1. Напри-
мер код Голея (23, 12, 7) (см. подраздел 1.4) также принадлежит классу кодов БЧХ, по-
