Непейвода Н.Н., Скопин И.Н. Основания программирования

Подождите немного. Документ загружается.

7.2. ПОТОКОВАЯ ОБРАБОТКА

305

Схема Пример

ИНИЦИАЛИЗАЦИЯ

int ch; int Sa=0, Sb=0, S=0;

пока ПОТОК НЕ ИСЧЕРПАН

цикл

while ((ch=getchar())!=’\n’)

ПОРОЖДЕНИЕ ОЧЕРЕДНОГО

ЭЛЕМЕНТ

{ //генерация вместе с проверкой

Выбор РАЗДЕЛЯЮЩЕЕ выраже-

ние

из

switch ( ch ) {

СПИСОК ЗНАЧЕНИЙ 1 :

case ’a’:

ОБРАБОТКА 1 ЭЛЕМЕНТА

Sa ++; break;

СПИСОК ЗНАЧЕНИЙ 2 :

case ’b’:

ОБРАБОТКА 2 ЭЛЕМЕНТА

Sb ++; break;

СПИСОК ЗНАЧЕНИЙ 3 :

...

иначе АЛЬТЕРНАТИВНАЯ ОБ-

РАБ

ОТКА

default: S ++; }

конец цикла

}

ЗАВЕРШЕНИЕ

printf ("Sa=%i, Sb=%i, S=%i,\n

Total=%i \n",Sa,Sb,S

,Sa+Sb+S);

Таблица 7.11. Разделение обработки на несколько потоков. Используется

оператор выбора

N-ых простых чисел для использования (распечатки) запоминание по-

зволяет ставить вопрос о том,что,быть может,искомое число уже ранее

было найдено, и процесс поиска-вычисления можно заменить извлече-

нием нужного числа из хранилища;

• Прерывание-возобновление вычислительного процесса. Нет необходи-

мости запускать повторный поиск простого числа с самого начала, ко-

гда найдены некоторые предшествующие ему числа. Можно просто за-

пустить продолжение ранее прерванного процесса.

Из этого видно, что стратегия решения задач существенно зависит от того,

какие средства программист предполагает использовать для запоминания.

Применительно к задаче о простых числах первое, что стоит проанали-

зировать, — это возможность использования массива как структуры данных

языка в качестве хранилища ранее найденных простых чисел.

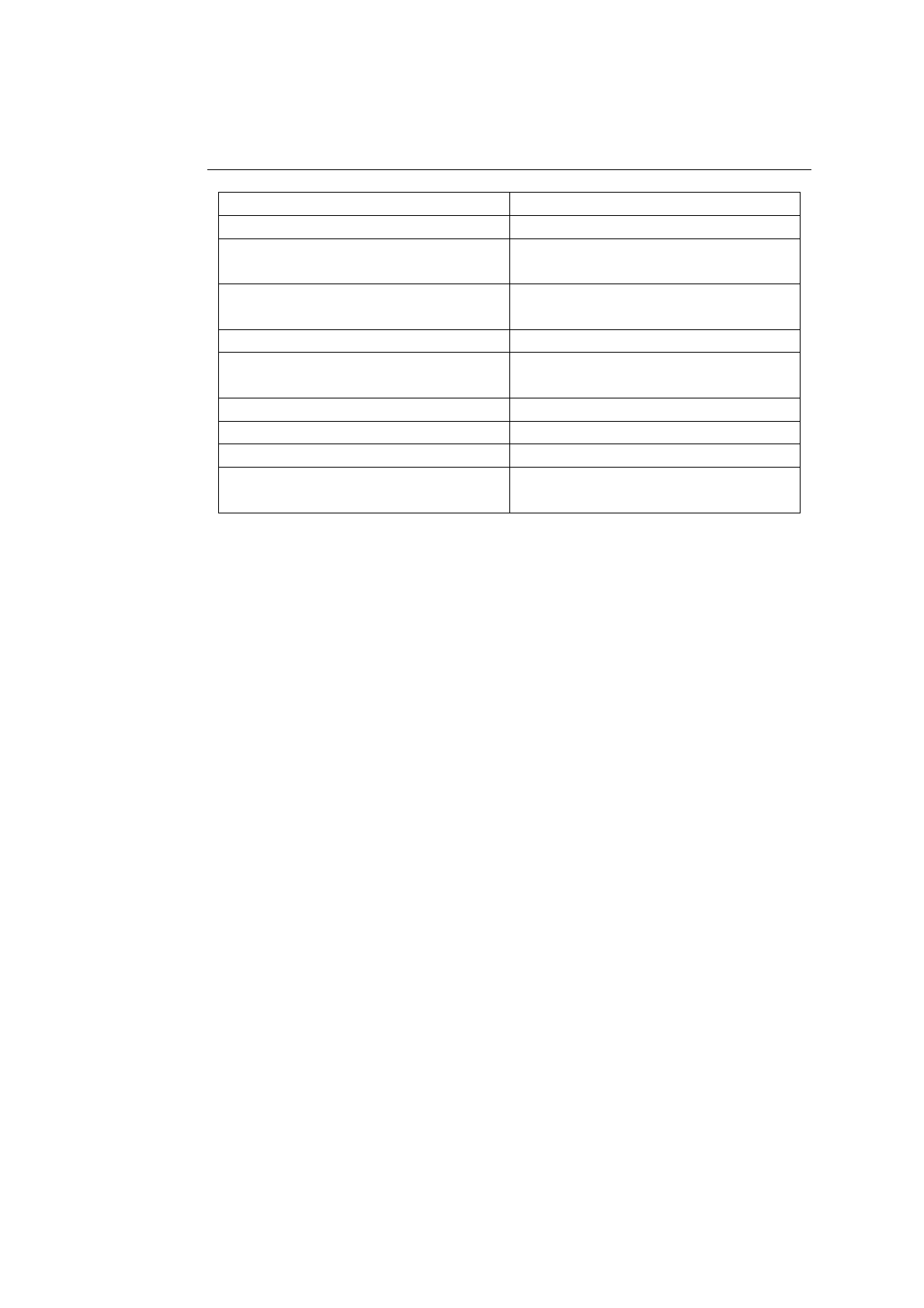
306

ГЛАВА 7. ЦИКЛИЧЕСКИЕ ВЫЧИСЛЕНИЯ

Схема Пример

ИНИЦИАЛИЗАЦИЯ

char ch; int I=0;

пока ПОТОК НЕ ИСЧЕРПАН

цикл

while ((ch=getchar())!=’\n’)

ПОРОЖДЕНИЕ ОЧЕРЕДНОГО

ЭЛЕМЕНТ

{ //генерация вместе с проверкой

ПРЕДОБРАБОТКА ЭЛЕМЕНТА

I ++;

Если УСЛОВИЕ ВЫХОДА

if ( ch == ’a’ ) {

То ОБРАБОТКА 1 ЭЛЕМЕНТА

printf ("№первого a=%i",I);

ВЫХОД ИЗ ЦИКЛА

break;

ПОСТОБРАБОТКА ЭЛЕМЕНТА

// постобработка отсутствует

конец цикла

}

ЗАВЕРШЕНИЕ

if ( ch == ’\n’)

printf ("букв a нет

!");

Таблица 7.12. Используется принудительный выход из цикла (пример)

Программа 7.2.2

/* Prime_Numbers_2.

Распечатка N-ого простого числа,

использование массива

#include <stdio.h>

#include <math.h>

int N,i,j,k;

int Prime;

int a[1000];

int main(void) {

printf("Write N:");

scanf("%i",&N);

a[1]=1;

a[2]=2;

k=2;

if (N<=0)

printf("При N <= 0 простых чисел не существует \n");

else {

i=1;

while (k<N) {

i+=2;

7.2. ПОТОКОВАЯ ОБРАБОТКА

307

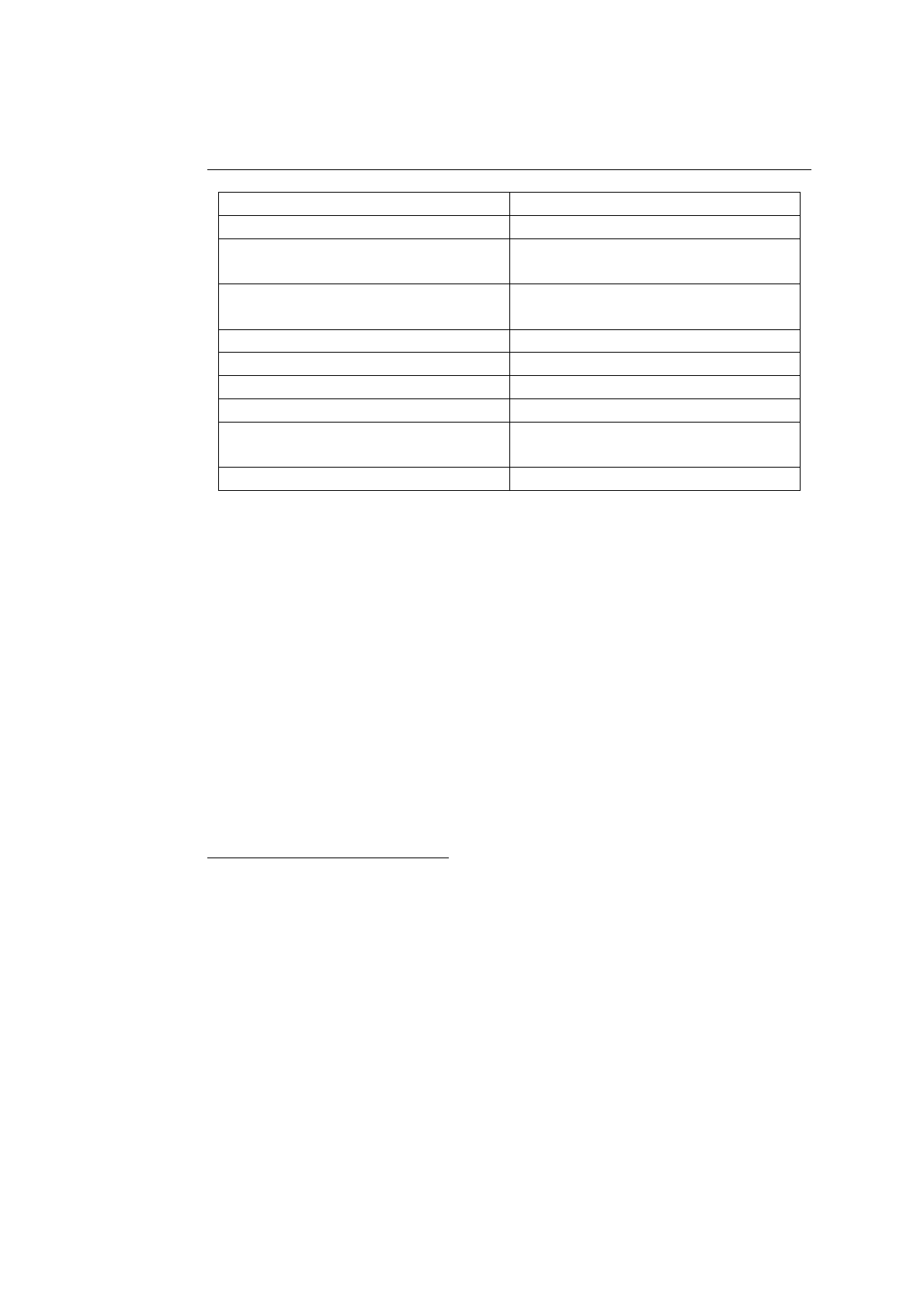
Схема Пример

Если в языке можно использовать

операторы завершения, то про-

грамма улучшается:

— нет нужды в каскадном за-

вершении;

— исчезают избыточные про-

верки;

— повышается наглядность

программы.

:МеткаУровня: пока

((ch=getchar())!=’\n’)

цикл если ( ch == ’a’ )

то printf ("№первого a=%i",I);

завершить МеткаУровня

все

иначе printf ("букв a нет!");

иначе относится к циклу

все

Конструкция цикла и условий

взята из языка

ЯРМО */

Таблица 7.13. Цикл с выходом из уровня

for( j=2, Prime = true; Prime && a[j]<=sqrt(i); j++)

Prime = i%a[j];

if (Prime) a[++k] = i;

}

printf("%i-ое простое число = %i\n", N, i);

}

return 0;

}

Эта программа не сложнее

Prime_Numbers_1

(внешне она выглядит даже

проще, т. к. текст не перегружен комментариями, использованными ранее

для разъяснения потоковой обработки, нет нужды в общей части вывода ре-

зультата, вместо которой инициализируются два первых значения массива и

др.) Не следует опасаться неэффективности в связи с тем, что в условии за-

вершения цикла

for

выражение обращается к вызову функции

(sqrt(i))

. Все,

что может быть вычислено вне итераций цикла, будет вынесено транслято-

ром до цикла. По аналогичным причинам, значение переменной с индексом

a[j]

не будет извлекаться из массива дважды.Несколько сложнее дело обстоит

с двойным вычислением истинности

Prime

: во время проверки условия окон-

чания цикла и после цикла. Не всякий транслятор сможет выстроить вычи-

сления так, чтобы исключался повторный счет. Однако, даже если в данной

системе программирования такая оптимизация не предусматривается, это не

страшно: лишняя проверка условия выполняется вне внутреннего цикла, а

308

ГЛАВА 7. ЦИКЛИЧЕСКИЕ ВЫЧИСЛЕНИЯ

Схема Пример

ИНИЦИАЛИЗАЦИЯ

char ch;

пока ПОТОК НЕ ИСЧЕРПАН

цикл

while ((ch=getchar())!=’\n’)

ГЕНЕРАЦИЯ ОЧЕРЕДНОГО

ЭЛЕМЕНТ

{ //генерация вместе с проверкой

ПРЕДОБРАБОТКА ЭЛЕМЕНТА

// предобработка отсутствует

если УСЛОВИЕ ВЫХОДА

if ( ch == ’a’ )

то ОБРАБОТКА 1 ЭЛЕМЕНТА

// пропуск буквы a

ВЫХОД ИЗ ИТЕРАЦИИ

continue;

ПОСТОБРАБОТКА ЭЛЕМЕНТА

printf ("%c", ch);

конец цикла

}

ЗАВЕРШЕНИЕ

printf (’\n’);

Таблица 7.14. Используется принудительный выход из итерации (пример)

потому на эффективности вычислений она практически не скажется, а устра-

нение этой мелочи испортит другие характеристики программы.

Одной из структур данных, естественно ассоциированных с потоковым

вычислением, и, соответственно, со многими видами циклов, является мас-

сив. Массив, как и каждая структура данных, имеющаяся в программирова-

нии, должен рассматриваться с двух сторон.

• Чем является данная структура, какова математическая и прагматиче-

ская сущность данной структуры?

• Как она представляется в программе?

С точки зрения математики и прагматики можно дать следующее определе-

ние.

Решение этой проблемы, убивающее двух зайцев сразу, может быть дано с помощью

структурного перехода:

for (j=2, Prime=true;a[j]<=sqrt(i);j++)

if (Prime=i%a[j])

//Присваивание, совмещенное с проверкой

{

a[++k]=i;

break; };

7.2. ПОТОКОВАЯ ОБРАБОТКА

309

Определение 7.2.4. Массив элементов типа

с индексами из

—функция,

перерабатывающая индексы в элементы,значения которой запоминаются при

их первом вычислении и поэтому практически не требуют ресурсов для по-

вторного вычисления.

Конец определения 7.2.4.

Итак, массив — предвычисленная функция. В таком случае присваивание

элементу массива — несколько неточное обозначение. Это на самом деле

действие над всем массивом.

Но, в соответствии с духом структурного про-

граммирования, в котором действия локальны, можно не акцентировать вни-

мание на данном обстоятельстве, хорошо разобранном, в частности, в книге

Гриса [27].

Вторая сторона структуры данных —как ее представляют. Для нас прак-

тически неважно, что массив обычно занимает в памяти связный сегмент;

важно, что он размещается в памяти и что операция вычисления элемента

массива по его индексу очень быстрая. Линейное расположение элементов

массива — всего лишь один из способов обеспечить эти требования. Ограни-

чения, накладываемые традиционной реализацией, заложенной в стандарты

большинства языков, привели к тому, что в большинстве языков массив вос-

принимается как функция из статически заданного линейно упорядоченного

множества индексов. Поэтому естественная конструкция типа

int n;

Read(n);

int[1:n] a;

недопустима в языках

Pascal

Подобные возможности предоставляют

Algol-60

Алгол-68

.Массивы,раз-

мер которых вычисляется и фиксируктся в момент исполнения их описания,

получили название динамических массивов, в отличие от статических мас-

сивов яызков

Pascal

. Но в ряде случаев в момент исполнения описания

массива мы еще не знаем, какого размера память будет требоваться, и тогда

хотелось бы иметь возможность наращивать массив по мере необходимости,

а также отказываться от памяти. В

Алголе-68

подобные массивы называются

гибкими или подвижными (ﬂexible).

Начало Microsoft-speciﬁc фрагмента

Поскольку такая конструкция необходима, особенно при обмене данными

Пожалуй, впервые на это обратил внимание Хоор в книге [29]

310

ГЛАВА 7. ЦИКЛИЧЕСКИЕ ВЫЧИСЛЕНИЯ

между удаленными программами, она была введена через “черный ход”: че-

рез тип данных

Variant

, который является потенциально бесконечным объ-

единением типов. В частности, значениями типа

Variant

могут быть гибкие

массивы,имеющие тип

SafeArray

.Для гибких массивов имеется специальная

операция создания такого массива. Работу с гибкими массивами иллюстри-

рует следующий фрагмент програмы.

Программа 7.2.3

unsigned int n;

ﬂoat x,y;

long i;

scanf(&n,&x);

SAFEARRAY *pSa = NULL;

SAFEARRAYBOUND sabound[1];

sabound[0].lLbound = 1;

sabound[0].cElements = n;

pSa = SafeArrayCreate(VT_R4, 1, sabound);

i=5;

SafeArrayPutElement(psa, &i,&x);

SafeArrayGetElement(psa, &i, &y);

if(x!=y){return -1;}

scanf(&sabound[0].cElements);

SafeArrayRedim(psa,sabound);

Здесь мы вначале формируем структуру из граничных пар массива (он не обя-

зательно начинается с 0!) Затем создаем массив действительных чисел (тип

элементов задается константой

VT_R4

) нужной нам длины. Затем мы запи-

сываем в него элемент, читаем этот элемент, проверяем корректность опе-

раций,

и, наконец, изменяем границы массива. Cпособ работы с гибкими

массивами через тип данных

SafeArray

стал практически общепринятым в

сегодняшней практике.

Конец Microsoft-speciﬁc фрагмента

При первом же просмотре текста программы

Prime_Numbers_2

, возни-

кает законный вопрос: откуда взялось число 1000 для количества элементов

массива? Обсуждение этого решения дается в таблице 7.15.

Не беспокойтесь о возможном нарушении защиты памяти! Каждая операция с

SafeArray

проверяет значения индексов и не допускает их выхода за границы.

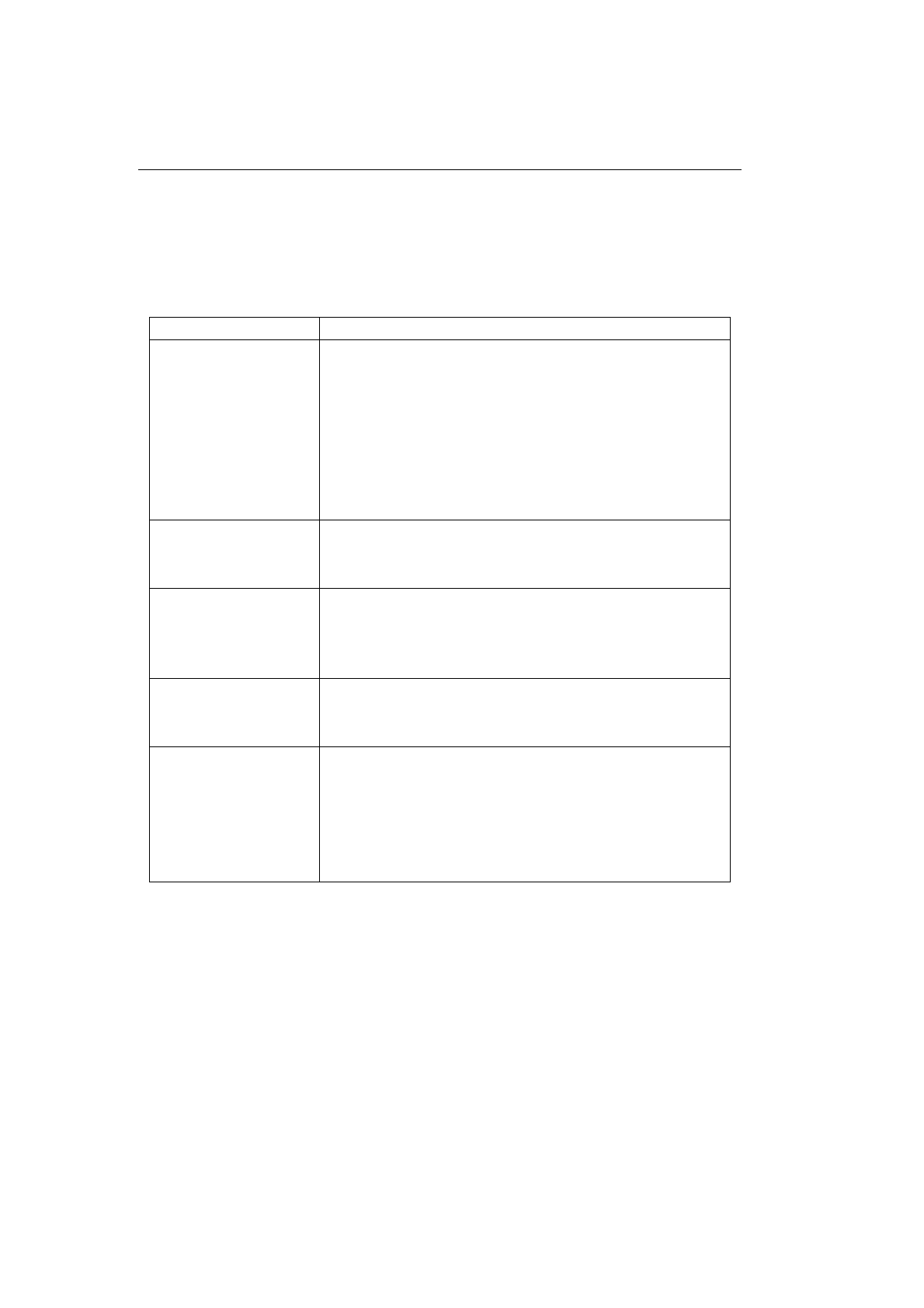
7.2. ПОТОКОВАЯ ОБРАБОТКА

311

Варианты ответов Возражения

a) Я не буду ис-

пользовать числа,

превосходящие

1000

1. Кто-то другой (или сам автор через опреде-

ленное время) окажется в роли неосведомленного

пользователя

;

2. Использование программы, как части некото-

рой системы, в которой нужна реакция на все слу-

чаи вычислений

;

3. Модификация и развитие программы

b) 1000 хватит на

все случаи жизни

1. Программа ненадежна, т. к. иногда она ведет се-

бя непредсказуемо;

2. Все случаи жизни предусмотреть невозможно

c) Если надо, легко

заменить 1000 на

большее

число

1. Это не так, когда размеры простых чисел ока-

зываются превосходящими емкость значения ти-

па

int

;

2. Это не так, когда требуется экономить память

d) Почему бы не

воспользоваться

SafeArray

Ну вот еще, буду я пользоваться чем-то, приду-

манным Microsoft! Я работаю в стандарте

e) ... Общее возражение: подмена вычисления извле-

чением значения и механизм прерывания-возоб-

новления вычислительного процесса ограниче-

ны лишь теми случаями, когда программу можно

встроить в использующую программу (например,

с циклическими запросами) лишь как текст

Таблица 7.15. Обсуждение числа элементов массива

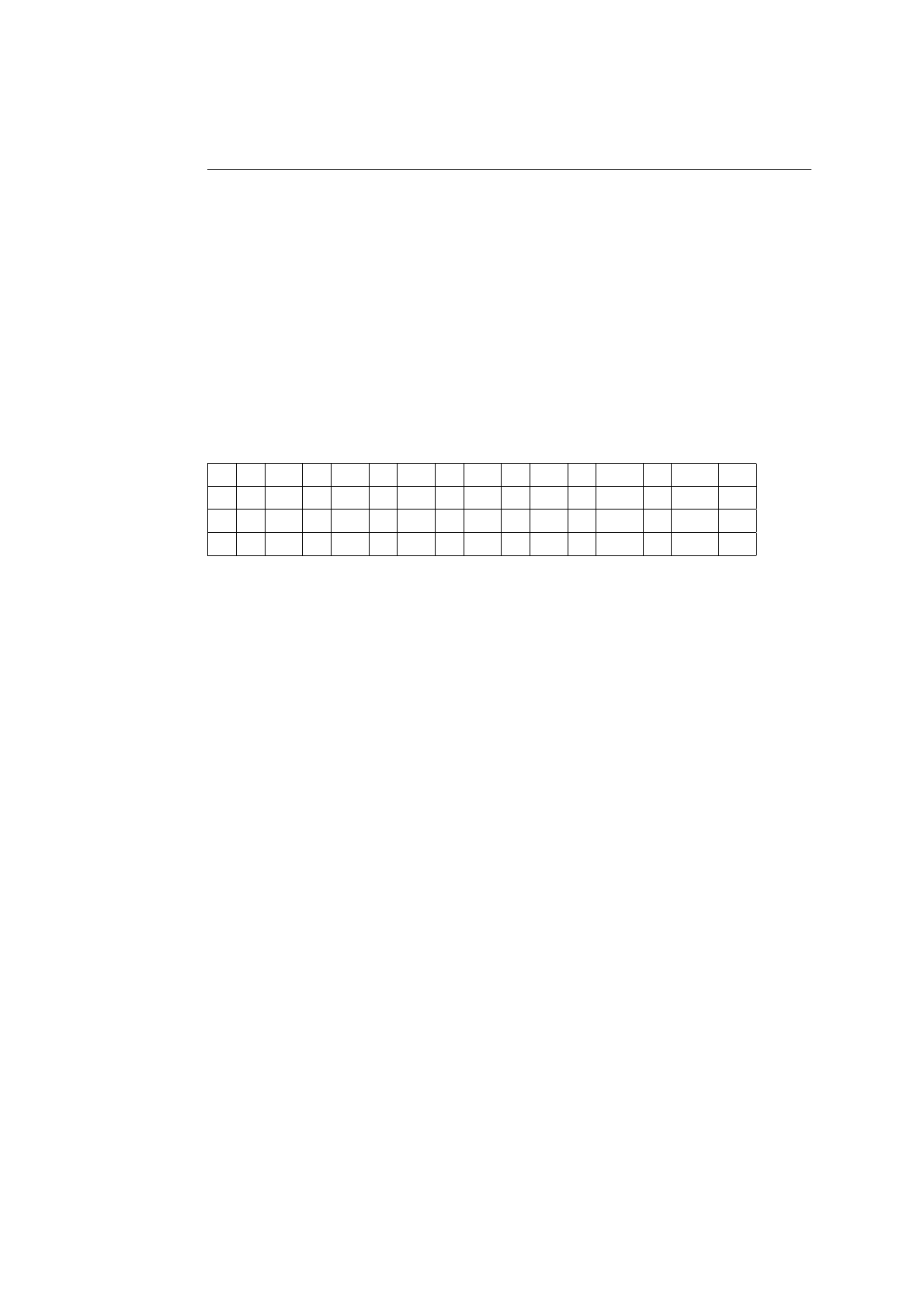
312

ГЛАВА 7. ЦИКЛИЧЕСКИЕ ВЫЧИСЛЕНИЯ

Надежность программы можно (и нужно!) повысить путем встраивания

дополнительной проверки того, что N не превосходит размера массива

Но это не избавит от необходимости учета того, что размер ячейки может

оказаться недостаточным для хранения очередного простого числа. А если

воспользоваться типом

double int

для массива

, то это удвоит потребность

в памяти. Таким образом, размеры массива должны быть согласованы с раз-

мерами хранимых в нем значений.

Сократить потребности в памяти при решении запоминать ранее найден-

ные простые числа можно, если хранить не сами числа, а разности соседних

простых чисел. Разности требуют существенно меньше места, чем сами чи-

сла. Это видно уже из сопоставления указанных величин для начала после-

довательности простых чисел

1 - 7 2 19 2 37 6 53 6 71 4 89 6 107 4

2 1 11 4 23 4 41 4 59 4 73 2 97 8 109 2

3 1 13 2 29 6 43 2 61 2 79 6 101 4 113 4

5 2 17 4 31 2 47 4 67 6 83 4 103 2 127 14

Разумеется, таких наблюдений недостаточно, требуется математическая

проработка вопроса, чтобы определить, насколько оправдан переход к разно-

стям, когда и как скажется эффект разницы роста скоростей двух последова-

тельностей и т. д. При этом надо помнить и о том, что хранение разностей

потребует дополнительно разработать алгоритм перехода от разностей к са-

мим простым числам (чуть ниже будет показано, что можно согласовать ра-

боту этого алгоритма с организацией проверки простоты очередного числа).

Еще один важный вопрос, в связи с программой

Prime_Numbers_2

, о том,

почему выбрана проверка простоты числа i в данном порядке.Исходные усло-

вия для организации проверки минимальны: наличие множества найденных

простых чисел, не превосходящих i. Никаких предположений об упорядо-

ченности этого множества нет. Да и не нужны они, если речь идет о матема-

тической задаче. Способ порождения этого множества таков, что его элемен-

ты появляются в соответствии с последовательностью простых чисел. Если

бы явно требовался другой порядок, его нужно было бы построить. Если же

не требуется никакой порядок, то, в частности, можно остановиться на по-

рядке порождения, как целесообразно для решаемой задачи, поскольку ве-

роятность делимости числа на малые числа выше, чем на большие. Это на-

блюдение использовано в программе

Prime_Numbers_2

при выборе порядка

итераций проверочного цикла:

for( j=2, Prime = true; Prime && a[j]<=sqrt(i); j++)

7.2. ПОТОКОВАЯ ОБРАБОТКА

313

Prime = i%a[j];

Данный порядок оказывается согласованным с решением о хранении разно-

стей вместо значений простых чисел. В самом деле, он предполагает после-

довательный перебор простых чисел от меньшего к большему. При хранении

разностей именно такой перебор можно реализовать за одно сложение.

Prime_Numbers_2

не учитывает возможности перехода на новые позиции

рассмотрения решаемой задачи, связанные с долговременным хранением ре-

зультатов счета. И замена вычисления извлечением значения, и механизм

прерывания-возобновления вычислительного процесса ограничены лишь те-

ми случаями, когда программу можно встроить в использующую программу

(например, с циклическими запросами) лишь как текст. Но и в этом случае

применение

Prime_Numbers_2

не приведет к экономии счета: все простые

числа будут повторно вычисляться, а не извлекаться. Соответствующая мо-

дификация

Prime_Numbers_2

представлена следующей программой.

Программа 7.2.4

Распечатка N-ого простого числа, переиспользование вычислений.

/* Prime_Numbers_3. */

#include <stdio.h>

#include <math.h>

int N,i,j,k;

int Prime;

int a[1000];

int main(void) {

a[1]=1;

a[2]=2;

a[3]=3; //!

k=3; //!

do {

printf("Write N:");

scanf ("%i",&N);

if (N<=0)

printf("При N <= 0 простых чисел не существует \n");

else {

if (k>=N) i = a[N]; //!

else { //!

i=a[k]; //!

314

ГЛАВА 7. ЦИКЛИЧЕСКИЕ ВЫЧИСЛЕНИЯ

while (k<N) {

i+=2;

for( j=2, Prime = 1; Prime && a[j]<=sqrt(i); j++)

Prime=i%a[j];

if (Prime) a[++k]=i;

}

} //!

printf("%i-ое простое число = %i\n", N, i);

}

scanf("%c",&N);

}

while (N !=’n’); //признак конца счета

return 0;

}

Prime_Numbers_3

курсивом отмечены строки, добавленные для организа-

ции цикла, а знаками

//!

выделены изменения и добавления, сделанные для

организации переиспользования.

Может показаться неочевидной модификация инициализации массива,т.е.

присваивание значения его третьему элементу, и, соответственно, оператор

k = 3;

Это сделано из следующих соображений. Просмотр потока лишь не-

четных чисел делает избыточной проверку делимости на два. В то же время

надо позаботиться о том,чтобы начало просмотра новых нечетных чисел бы-

ло корректным как на первой итерации цикла, так и в дальнейшем. Иными

словами, требуется, чтобы оператор

i = a[k];

приводил к нечетному i в обоих

случаях. Присваивать k единицу нельзя — на нее делятся все числа, а сле-

довательно, целесообразно выбрать минимальное простое нечетное число,

большее единицы, т. е. три.

Если требуется пользоваться результатами вычислений при разных запус-

ках программы (или в других программах) и при этом заменять вычисления

извлечениями значений, то естественным будет сохранение результатов ра-

боты программы в файле (и считывание предыдущих результатов из файла).

Изменения, требующиеся в этом случае, показаны в следующей программе.

Программа 7.2.5

Распечатка N-ого простого числа, файловая версия.

Prime_Numbers_4.

#include <stdio.h>