Непейвода Н.Н., Скопин И.Н. Основания программирования

Подождите немного. Документ загружается.

6.1. РАЗБОР СЛУЧАЕВ

275

вырабатывает значений всех <константных выражений>после “

case

”—ана-

лог варианта

иначе

в более логичных языках.

(как и в

Алголе-60

!) переход к выбираемому варианту не означает

того, что после завершения помеченного оператора управление будет пере-

дано в какое-то единственное для данного оператора выбора место в про-

грамме. После выполнения помеченного оператора управление передается

текстуально следующему оператору. Это правило влечет три следствия:

a) Если не выйти явно из выбранного варианта действий, то после его завер-

шения будет выполняться следующий оператор даже в тех случаях, когда

он помечен с помощью

case

или

default:

. Таким образом, могут выпол-

ниться подряд несколько вариантов действий, что почти всегда приводит

к недоразумениям и плохо понимаемому тексту программы, за исключе-

нием единственного случая, указанного в следующем пункте.

b) Следствием предыдущего в связи с тем, что в языке есть конструкция <пу-

стой оператор>, является возможность образовывать списки значений вы-

бора варианта действий. Это несколько подряд идущих фрагментов вида

“

case

” <константное выражение> “:”

c) Для прекращения выполнения оператора, входящего в “

switch

”“(”<усло-

вие> “)” <оператор>, следует использовать специальный оператор

break;

который передает управление оператору,текстуально следующему за пре-

кращаемым составным оператором (в данном случае за

switch

Таким образом, оператор выбора в языке

может быть записан с помощью

switch

-оператора, операторов с пометкой

case

и операторов

break

в при-

ближенном к предписанному в других языках виде. Правило хорошего тона

программирования: использовать

switch

-оператор только так, как описано

выше.

С учетом сказанного,реализация калькулятора демонстрируется програм-

мой 6.1.2, которая написана с соблюдением указанных соглашений.

Программа 6.1.2

Оператор

break;

является первым из рассматриваемых нами операторов структурного пе-

рехода, о которых упоминалось в главе о стилях программирования (см., напр., программу

3.3.1). Здесь его использование просто навязывается недоработками языка

C/C++

, а в дру-

гих случаях структурные переходы будут возникать как удобное средство прояснить логику

программы.

276

ГЛАВА 6. РАЗВЕТВЛЕНИЕ ВЫЧИСЛЕНИЙ

#include <stdio.h>

#include <math.h>

/* определим коды возврата программы */

#deﬁne OK 0

#deﬁne SYNTAX_ERROR -1

#deﬁne BAD_OPERATION -2

#deﬁne ZERO_DIVISION -3

int main()

{

ﬂoat x, y, result;

char operation;

printf( ”Введите выражение для вычисления в виде \n” );

printf(”<число><операция><число>:\n”);

ввод выражения с проверкой, что все три поля введены успешно

if ( 3 != scanf( ”%f%c%f”, &x, &operation, &y ) )

{

printf( ”Синтаксическая ошибка!\n”);

return SYNTAX_ERROR;

выход из программы с кодом ошибки

}

printf( ”Введено выражение %f %c %f\n”, x, operation, y );

switch( operation )

{

case ’+’:

result = x + y;

break;

case ’-’:

result = x - y;

break;

case ’*’:

result = x * y;

break;

case ’/’:

if ( y == 0.0 )

6.1. РАЗБОР СЛУЧАЕВ

277

{

printf( ”Попытка деления на 0!\n”);

return ZERO_DIVISION;

выход с кодом ошибки

}

result = x / y;

break;

default:

printf( ”Недопустимый код операции: %c\n”, operation );

return BAD_OPERATION;

выход из программы с кодом ошибки

}

printf( ”Результат = %f\n”, result );

return 0; /*

нормальное завершение

}

В других языках конструкция выбора представляется более логично. На-

пример, в языке

Pascal

выбор реализуется синтаксически единым операто-

ром вида

case <параметр выбора> of

<Список значений_1>: <Действие_1>;

<Список значений_2>: <Действие_2>;

...

<Список значений_n>: <Действие_n>;

end;

Здесь каждый список значений — последовательность констант того же ти-

па, что и параметр выбора, разделенных запятыми.

В стандарте языка

Pascal

a) не предусматривается вариант иначе (следовательно, при необходимости

программист должен сам встраивать в программу нужные проверки);

b) требуется, чтобы все значения списков были константами;

c) явно оговаривается неопределенность результата выполнения оператора

выбора, если значение выражения не входит в объединение списков зна-

чений (как всегда в подобных случаях, неопределенность ликвидирует-

ся при конкретной реализации языка так, как это удобно разработчикам

транслятора).

278

ГЛАВА 6. РАЗВЕТВЛЕНИЕ ВЫЧИСЛЕНИЙ

В расширении языка

Pascal

,используемом системами программирования

Turbo-

Pascal

Delphi

, последним членом оператора

case

может быть вариант

else

Аналогична трактовка оператора выбора в

Алголе-68

, но там разрешает-

ся и вариант иначе, и динамическое вычисление значений, определяющих

выбор действий (что логически последовательнее, но несколько затрудняет

реализацию).

Различия операторов выбора обусловлены тем, что разработчики языко

по-разному решали задачу поддержки алгоритмов трансляции. Так, схема

трансляции

case

стандартного языка

Pascal

точно соответствует переключа-

тельной схеме, а

Алгол-68

требует, чтобы оптимально реализуемые варианты

case распознавались бы транслятором, что предполагает большую изощрен-

ность его реализации.

6.1.3. Типы данных, связанные с разветвлением

Каждому типу операторов соответствуют свои типы данных. Один из ти-

пов данных, связанных с разветвлением, приобрел практически абсолютный

характер для языков программирования. Это — тип логических значений,

обеспечивающий бинарный выбор и вычисления по формулам булевой ло-

гики.

Разборам случаев соответствуют структуры с объединениями (называе-

мые также вариантные структуры и просто объединения). В языках

C/C++

из-за отмеченных ранее несообразностей (см. стр. 62) такие структуры прак-

тически обязаны иметь частную форму, подобную следующей:

struct tagged

{

int type_tag;

union

{

int x;

ﬂoat y;

char a;

}

Для операций с вариантной структурой следует организовать переключе-

ние случаев по значению

type_tag

и в каждом случае работать с соответству-

6.1. РАЗБОР СЛУЧАЕВ

279

ющим вариантом структуры. Примером служит следующий фрагмент про-

граммы.

Программа 6.1.3

typedef struct

{

int type_tag;

union

{

int x;

ﬂoat y;

char a;

}

} tagged;

void smart_read(tagged *element);

{

...

}

int main();

tagged aa;

{

smart_read(&aa);

switch (aa->type_tag)

{

case 1: {process_integer(aa->x);break;};

case 2: {process_real(aa->y);break;};

case 3: {process_char(aa->a);break;};

}

...

}

Здесь функция умного чтения распознает, какого типа значение было введе-

но, и в соответствии с этим устанавливает тег в своем результате. По значе-

нию тега выбирается представление данных, соответствующее содержимому

переменной

Именно подобное представление естественно и для результата, и для ар-

гумента оператора разбора случаев, если разобраться в логическом смысле

дизъюнкции. В самом деле, когда мы разбираем случаи A

∨ ··· ∨ A

, мы

280

ГЛАВА 6. РАЗВЕТВЛЕНИЕ ВЫЧИСЛЕНИЙ

в каждом из случаев A

знаем, какой из результатов B

получится, и затем

собираем эти (возможно, совершенно разнородные) члены в единую дизъ-

юнкцию B

∨ ··· ∨ B

. Наоборот, разбирая дизъюнкцию, мы каждый раз

знаем, какой именно случай мы разбираем, и в зависимости от этого выби-

раем соответствующее предположение A

. Итак, доказав дизъюнкцию, мы

создаем значение, для которого в каждый конкретный момент нам известен

и индекс выполненного варианта, и соотвествующие этому индексу данные.

А разбирая дизъюнкцию, мы перебираем все варианты, и в каждом случае

рассматриваем только те данные, которые нужны.

Решение, предагаемое в языке

Pascal

, намного логичнее и красивее, чем

предложенное в

C/C++/C#

.Как уже говорилось, в этом языке вариантная струк-

тура обязательно предполагает тег, по которому выбирается один из вариан-

тов:

Программа 6.1.4

type tag=(star,planet, comet);

type data=record

case tg: tag of

star: (sd: star_data);

planet: (pd: planet_data);

comet: (cd:comet_data);

end;

...

begin

with data do

case tg of

star: Process_star(sd);

planet: Land(pd);

comet: Investigate(cd);

end;

...

end.

Алголе 68

было принято еще более последовательное, однако опять-

таки не доведенное до конца решение. Явного селектора при объединении

типов не задавалось, и единственным способом выбрать вариант из объеди-

нения было разобрать случаи,соответствующие объединявшимся типам, при

помощи оператора case (что в принципе правильно). Но имен у компонент

6.2. ТАБЛИЧНОЕ ЗАДАНИЕ

281

объединения не было предусмотрено, и поэтому при объединении одинако-

вые типы сливались (что уже в те времена было грубой концептуальной не-

доработкой).

§ 6.2. ТАБЛИЧНОЕ ЗАДАНИЕ РАЗВЕТВЛЕНИЙ

И ОПЕРАТОР ВЫБОРА ДЕЙКСТРЫ

Булевы выражения,условные операторы с

elif

,оператор выбора —все это

примеры приемов программирования, которые оказались удачными с точки

зрения качества (надежности)программ. Поэтому они стали стандартизован-

ными и, как следствие, обрели языковые формы. Но это далеко не единствен-

ные примеры даже для задания разветвлений в программах. Рассмотрим еще

два важных случая.

6.2.1. Таблицы решений

Сегодня этот метод анализа условий, кажется, уже прочно забыт. Тем не

менее, он весьма поучителен как с точки зрения обсуждения понятий языков

программирования, так и в практическом плане. Таблицы решений — это

способ раздельного задания (обдумывания, анализа и т. п.) составных усло-

вий и действий, связанных с вариантами. Достоинством их является то, что

значительно облегчается учет всех возможных вариантов разветвлений. При

этом забота о последовательности проверок и об алгоритмизации вычисли-

тельного процесса относится к реализации данного метода, и программист

не обязан об этом думать.

В общем случае таблица решений (см. табл. 6.1) состоит из двух частей:

условий и действий. Каждое из условий представлено перечнем значений

так, чтобы в колонках таблицы оказались представлены все сочетания зна-

чений всех условий. В перечень значений чаще всего входят T — истина

и F — ложь; допускается также указание, что значение некоторого условия

для выбора действия безразлично, это отмечается знаком −. Часть действия

представлена перечнем наименований действий, а в колонках под значения-

ми условий указывается метка (Х), если действие при данном наборе значе-

ний должно быть выполнено.

Что дает программисту использование таблиц решений? Во-первых, ра-

ботая с данными и действиями, организованными таким способом, можно

гарантировать, что будут рассмотрены все возможные сочетания условий.

При желании можно написать программу, которая проверяет это свойство

автоматически. Во-вторых, таблицы решений дают метод декомпозиции за-

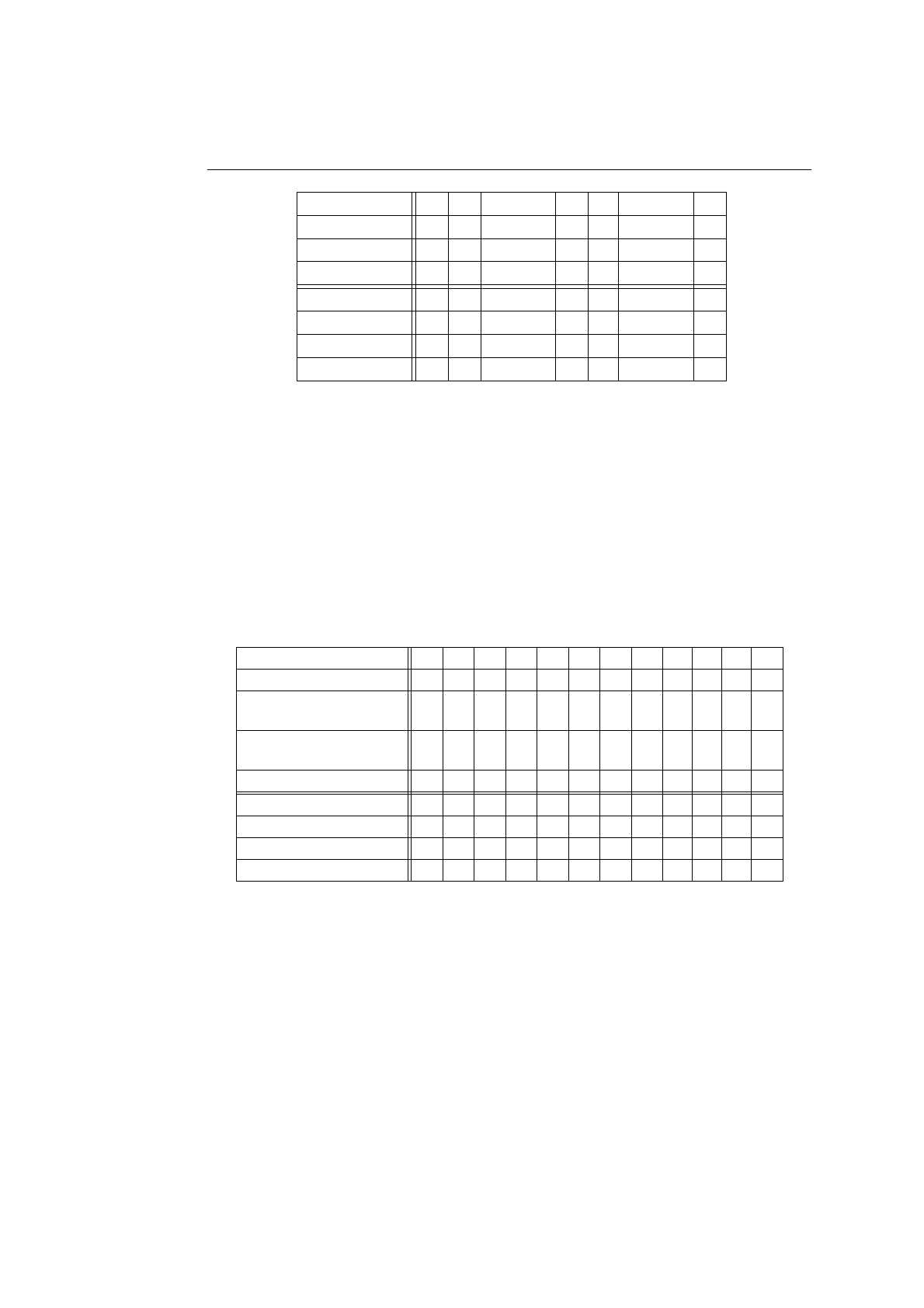
282

ГЛАВА 6. РАЗВЕТВЛЕНИЕ ВЫЧИСЛЕНИЙ

Условие 1 T T T T F

Условие

2 T T F F

Условие

N T F T F F

Действие

1 X X X

Действие

2 X X X

Действие

M X X

Таблица 6.1. Таблица решений

дачи: разделение анализа условий и решений о выполнении действий. Везде,

где есть необходимость такого разделения, полезно применять метод таблиц

решений хотя бы для анализа ситуаций.

Следующий пример преследует цели дать представление о применении

данного метода.Он связан с типичной задачей,для решения которой таблицы

решений хорошо подходят: обработка анкет. Пусть надо обработать опрос-

ные листы с вариантами ответов на вопросы, представленными в блоке усло-

вий таблицы 6.2. Эти условия соответствуют выделению в массиве исходных

Пол = муж T T T T T T

Нравится себ

е T T T T T T

Считает, что нравит-

ся др

угим

T T T T

Считает, что не нра-

вится др

угим

T T T T

Не

знает T T T T

Добавить к Г

M X X

Добавить к Г

P X X

Добавить к Г

T X

Добавить к Г

W X X X X X X

Таблица 6.2. Таблица решений для обработки анкет

данных следующих групп (которые можно интерпретировать, например, как

профпригодность кандидатов на менеджера, рекламного агента, техничку и

рабочего):

ГМ: Мужчины, нравящиеся себе и уверенные, что нравятся другим, и

6.2. ТАБЛИЧНОЕ ЗАДАНИЕ

283

женщины, нравящиеся себе, но которые не знают о мнении других о себе;

ГР: Все, кто себе нравится и считают, что нравятся другим;

ГТ: Женщины, которые себе не нравятся и считают, что они не нравятся другим;

ГW: Мужчины.

В соответствии с выбранными критериями принадлежности индивидуу-

ма к той или иной группе мы отмечаем в таблице нужные комбинации усло-

вий.Обработка одного опросного листа сводится к прочтению ответов,в ходе

которого выбирается действие (см. табл. 6.2).

Превращение таблиц решений в программу с условными операторами —

автоматизируемая задача. Другие достаточно легко реализуемые задачи, свя-

занные с методом таблиц решений: расстановка истинности условий, груп-

пировка (склейка) столбцов с одинаковыми действиями, перестановка столб-

цов по принципу близости действий и т. д.

При составлении таблицы решений возникает псевдопроблема: а что де-

лать, если выполнены условия двух различных действий? Нужно понимать,

что ничего страшного в этом нет. Слишком часто и в жизни мы сталкива-

емся с выбором, когда нет критериев для предпочтения одного из вариантов.

Конечно, лучше всего (для отладки программ) было бы, если программа при

наличии нескольких выполненных вариантов выбирала бы действие для ис-

полнения случайно, но важно хотя бы программисту четко понимать, что в

данном месте ему выбор конкретного действия безразличен.

6.2.2. Охраняемые команды

Э. Дейкстра превратил таблицы решений в определение условного опе-

ратора

→ S

. . . ,

→ S

ﬁ

(6.1)

Этот оператор практически является таблицей решений, в которой все усло-

вия уже выписаны явно. A

называется охраной оператора S

: доступ к S

284

ГЛАВА 6. РАЗВЕТВЛЕНИЕ ВЫЧИСЛЕНИЙ

возможен лишь при истинности условия охраны. Пример такого оператора

температура < 0 → замерзнуть;

температура > 0&температура < 100 → расплавиться;

температура > 100 → закипеть;

ﬁ

Возникает вопрос о том, что происходит, когда в операторе некоторые

случаи не предусмотрены и поданы такие данные,что ни одна из охран не вы-

полнена. Дейкстра предложил считать, что в этом случае программа должна

выдавать ошибку. Это решение хорошо теоретически, но никуда не годит-

ся практически. Если уж мы попали в непредусмотренную ситуацию, нужно

по крайней мере проанализировать ее самим и выдать толковое сообшение,

а не раздражающую всех, кроме программиста, отлаживающего программу,

строчку типа «

На с. 117 модуля Dubinda не выполнены условия охран

» (сра-

зу видно, что Дейкстра, предлагая решение, думал лишь о программисте, а

не о пользователе). Так что система охраняемых операторов обязана быть

полна!

Именно табличное задание операторов выбора лучше всего соответствует

их логической сути: разбору случаев в доказательстве.

Конструкция разбора

случаев имеет вид

Пусть доказано A

∨ ··· ∨ A

Если выполнено A

, то получается B

...

Если выполнено A

, то получается B

Значит, B

∨ ··· ∨ B

При разборе случаев они не обязаны исключать друг друга, и получающиеся

утверждения не обязаны все различаться.

Заметим, что в традиционной логике длительное время делалась та же концептуальная

ошибка, что и в нынешнем программировании: при разборе случаев обращалось внимание

на то, что случаи должны быть взаимоисключающими. Это требование избыточно в логике,

так же как и в программировании. А вот тем, что набор рассмотренных случаев должен быть

полон, пренебречь нельзя.

Наша формулировка формально эквивалентна тем, какие обычно приводятся в учебниках

логики, например, в [34].