Наумова Ж.Л. Начертательная геометрия: Учебное пособие
Подождите немного. Документ загружается.

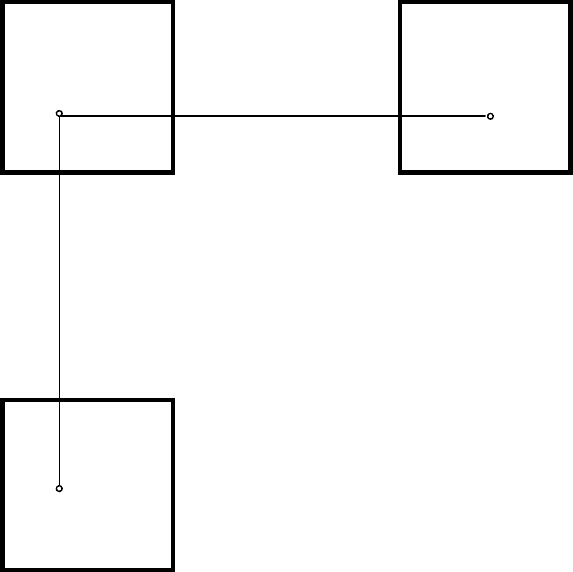
5. Дан куб с точкой А внутри. На комплексном чертеже построить:
1) точку В, симметричную точке А относительно верхней грани куба;
2) точку С, симметричную точке А относительно передней грани;
3) точку D, симметричную точке А относительно правого верхнего ребра;
4) точку Е, симметричную точке А относительно переднего нижнего ребра;
5) точку F, симметричную точке А относительно нижней передней правой
вершины.
A
2
A
3
A
1
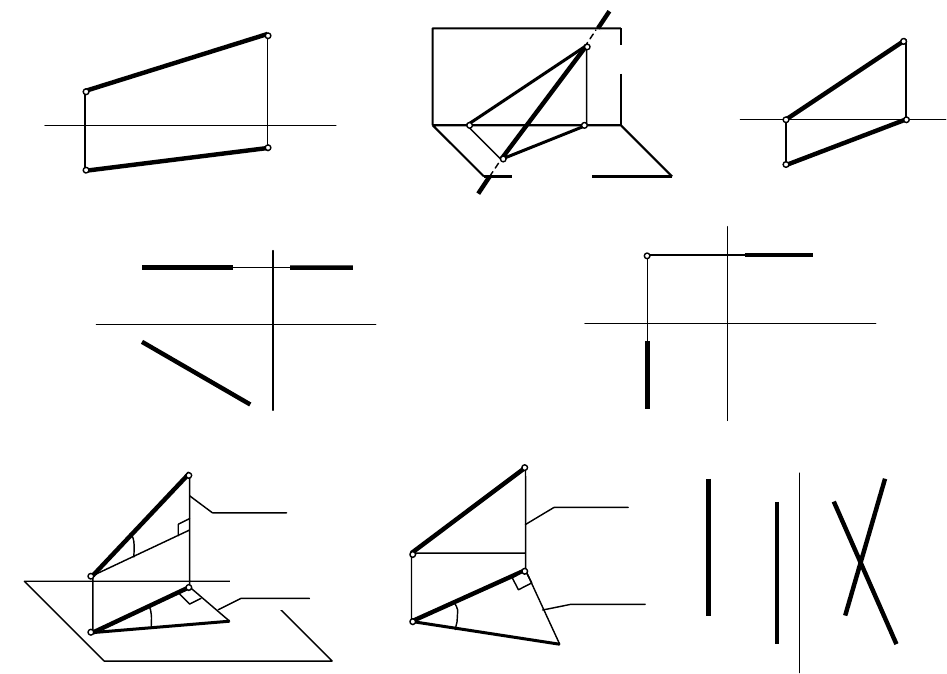
ПРЯМАЯ
Проекции прямой определяются проекциями двух её точек (рис. 2, а).
Проекциями прямой, в общем случае, являются прямые линии.
Следы прямой – это точки пересечения прямой с плоскостями проекций.
Одна из координат следа прямой равна нулю (рис. 2, б).
Прямые частного положения параллельны одной (прямые уровня) или
двум (проецирующие) плоскостям проекций. Две
проекции прямой уровня
параллельны разным осям проекций (рис. 2, в), две проекции проецирующей
прямой параллельны одной оси, а третья проекция вырождается в точку (рис. 2,
г).
Натуральная величина отрезка прямой общего положения определяется
величиной гипотенузы прямоугольного треугольника, построенного на одной
из проекций, как на катете. Второй катет треугольника равен разности
расстояний концов отрезка от той плоскости проекций, на которой взят первый
катет. Угол между гипотенузой и катетом-проекцией равен углу наклона
прямой к плоскости проекций, на которой треугольник построен (рис. 2, д).
Точка принадлежит прямой, если её проекции лежат на одноимённых
проекциях прямой и на одной линии связи (рис. 2, а,
б, д).
Для оценки взаимного положения прямых уровня следует построить их
проекции на плоскость, которой они параллельны (рис. 2, е).
а) б)
в) г)
д) е)
Рис. 2
А
2
х
А
1
В
1
В
2
x
z
y
y
O
h
2
h
1
h
3
y
x
z
y
O
i
1
i
2
i
3
A
B
П
B
A
Z
B
–
Z
B
–
a
2
b
2
a
3
b
2
z
B
B
A
A
Z
B
–
Z
B
–
M
2
N
1
N
≡N
2
M
≡ M
1
M
2
N
2
N
1
M
1
x
x
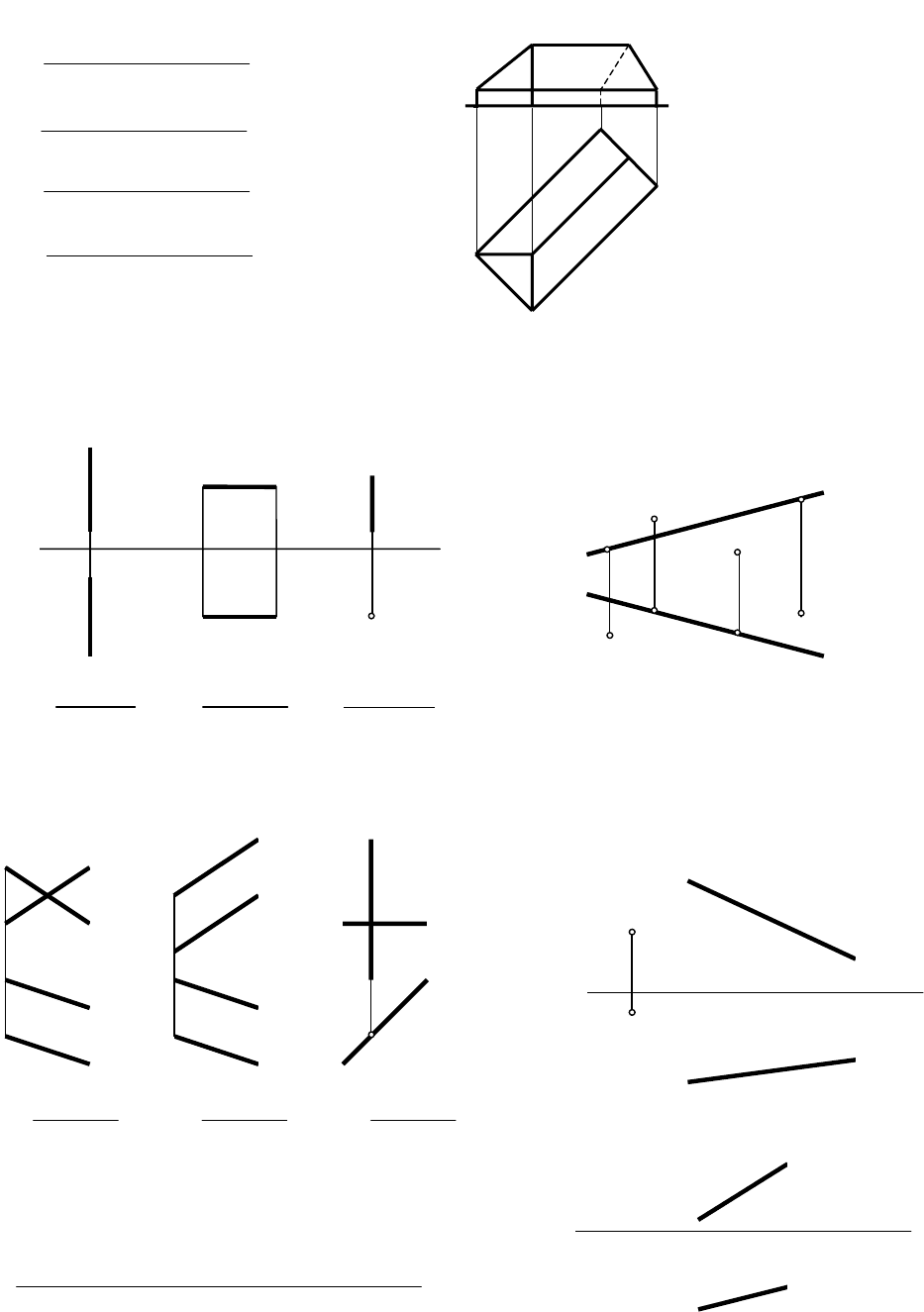
УПРАЖНЕНИЯ
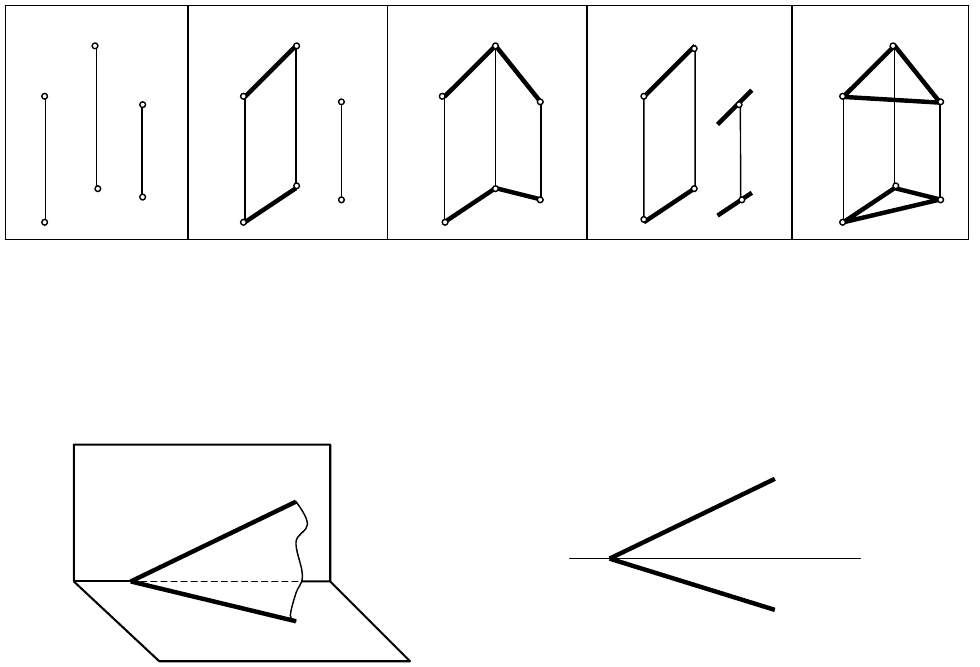
1. Какое положение относительно плоскостей проекций занимают рёбра
крыши?
D
2
C
2
AD_______________________________________________________________
BC
CD
DE
2. Как расположены прямые
(перпендикулярно или параллельно)
относительно плоскостей проекций?
3. Определить относительное
положение двух прямых.
4. Указать точки, расположенные:
а) под прямой;________________
б) перед прямой;______________
в) над прямой;________________
5. Через точку А провести
горизонтальную линию уровня h,
пересекающую прямую l.
Определить углы наклона прямых
к
П
1
.
6. На прямой m найти точку, высота
которой равна нулю. Как называется
эта точка?
E
1
A
2
A
1
C
1
B
2
E
2
B
1
D
1
A
2
m
2
n
2
n
1
m
1
a
2
b
2
a
1
b
1
c
2
d
2
c
1
d
1
l
2
l
1
x
A
2
A
1
l
2
l
1
x
B
1
1
2
1
1
2
2
2
1
3
1
3
2
4
2
4
1
l
2
l
1
E
2
C
2
D
2
F
2
B
2
C
1
D
1
E
1
≡F
1
A
1
x
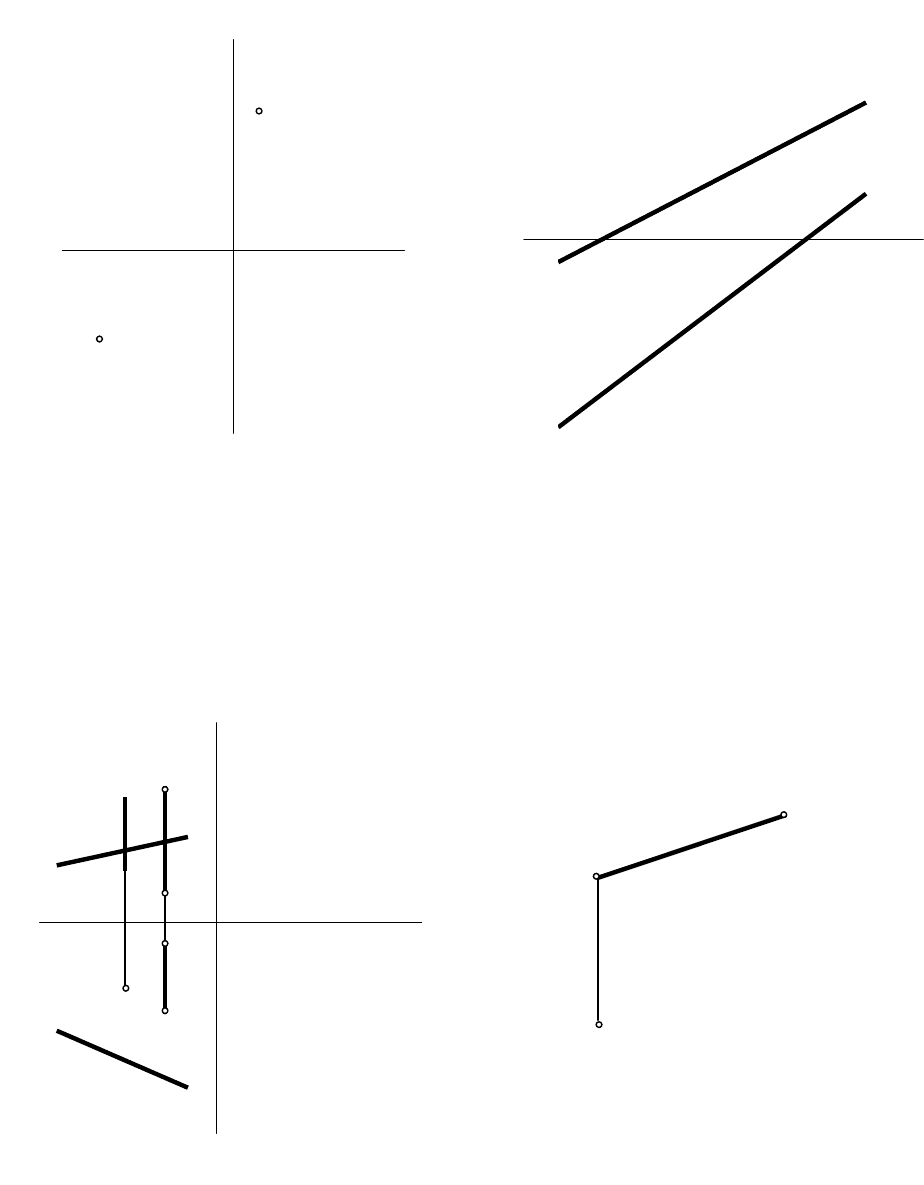
ЗАДАЧИ
1. По заданным проекциям следов прямой m (А
1
, В
3
) построить три её
проекции.
2. Построить проекции прямой m, параллельной прямой KL и пересекающей
прямые a и b.
l
2
l
1
x
O
z
y
x
y
K
1
L
1
a
1
L
2
x
y
z
O
b
1
a
2
b
2
K
2
A
2
A
1
A
1
B
3
B
2
y
3. Построить следы заданной прямой m и определить натуральную величину
расстояния между ними.
4. Дана фронтальная проекция А
2
В
2
отрезка прямой общего положения, равного
40 мм, и проекция А
1
его конца. Построить горизонтальную проекцию А
1
В
1
этого отрезка.
ПЛОСКОСТЬ
Определитель плоскости – совокупность элементов плоскости с
указанием их взаимного расположения, выделяющая однозначно данную
плоскость из всего множества. Основной определитель плоскости – три точки,
не лежащие на одной прямой: Σ (А, В, С).
Перезадать плоскость – означает перейти от одного способа задания к
другому (рис. 3).
A
1
B
2
C
2
A
2
B
1
C
1
A
1
B
2
C
2
A
2
B
1
C
1
A
1
B
2
C
2
A
2
B
1
C
1
A
1
B
2
C
2
A
2
B
1
C
1
A
1
B
2
C
2
A
2
B
1
C
1
Рис. 3
Следы плоскости –
это линии пересечения плоскости с плоскостями
проекций. Задание плоскости следами является частным случаем задания её
двумя пересекающимися прямыми (рис. 4).
П
2
П
1
f
0
h
0
f
2
0
h
1
0
f
1
0
≡ h
2
0
х
х
Рис. 4
Плоскости частного положения перпендикулярны к одной
(проецирующие плоскости) или к двум (плоскости уровня) плоскостям
проекций. Проекции плоскостей на плоскости проекций, к которым они
перпендикулярны, вырождаются в прямые линии
. Эти прямые линии собирают
на себе одноимённые проекции всех элементов, расположенных в плоскости.
Прямая принадлежит плоскости, если она проходит через две точки,
заведомо лежащие в этой плоскости, или проходит через одну точку и
параллельна какой-либо прямой плоскости.
Точка принадлежит плоскости, если она принадлежит прямой, лежащей
в этой плоскости.
Линии
уровня плоскости начинают строить с той проекции, которая
параллельна оси проекций.
УПРАЖНЕНИЯ
1. На каких чертежах заданные прямые линии определяют плоскость?
а) б) в) г)
_______________________________
2. Как расположены по отношению к плоскостям проекций заданные
плоскости?
Σ (a ∩ b)_____ Г (d ∩ k)______ T (c ∩ b)______ ∆ (q ∩ l) _______
3. Определить, принадлежит ли точка М плоскости Г (a ║b).
а) б) в)
a
2
b
2
a
1
b
2
c
2
≡d
2
c
1
d
1
m
2
n
2
m
2
n
2
x
f
1
≡h
2
h
1
f
2
a
2
b
2
a
1
≡ b
1
d
2
k
2
k
1
d
1
c
2
c
1
b
2
b
1
q
2
≡l
2
q
1
l
1
b
2
a
2
a
1
b
1
b
2
a
2
a
1
b
1
a
2
b
2
a
1
≡ b
1
M
1
M
2
M
2
M
2
M
1
M
1
____________ _____________ ____________ ____________
4. На каких чертежах прямая l принадлежит плоскости Т, заданной прямыми a
и b?
а) б) в) г)
___________________________________
5. Провести в каждой из заданных плоскостей горизонталь на расстоянии 10 мм
от П
1
и прямую, параллельную фронтальной плоскости проекций, на
расстоянии 15 мм от П
2.
а) б) в)
6. Построить проекции произвольного треугольника АВС, лежащего в заданных
плоскостях.
Г (Г
1
) Т (N; h) ∆ (a ║ b)
a
2
b
2
l
2
a
1
b
1
l
1
a
2
l
2
b
2
a
1
l
1
b
1
a
2
≡b
2
≡l
2
a
1
l
1
b
1
l
2
a
2
a
1
b
1
l
1
m
2
n
2
n
1
m
1
x
T
1
x
f
2
x
h
1
f
1
≡h
2
h
2
h
1
N
2
N
1
Г
1
a
2
a
1
≡b
2
b
1
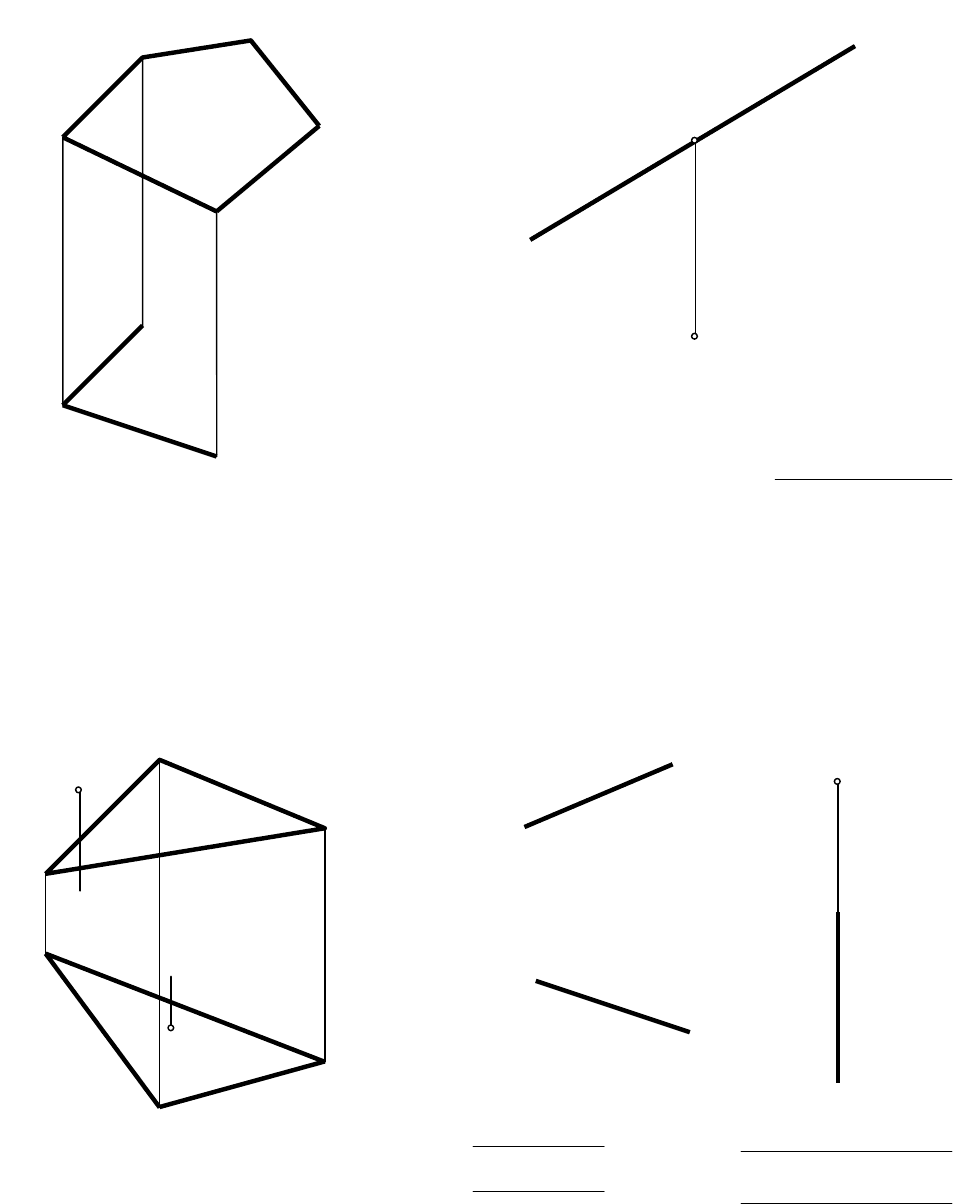
ЗАДАЧИ
1. Достроить горизонтальную
проекцию плоского пятиугольника
ABCDE.
2. Найти недостающие проекции
точек M и N, принадлежащих
плоскости T (∆ ABC). Через точку M
провести в плоскости горизонталь h,
а через точку N - фронталь f.
3. В плоскости Г (Г
2
) построить
окружность диаметром 30 мм с
центром в точке О. Определить и
записать величину большой и малой
осей эллипса.
C
2
B
2
4. Через прямую a провести
плоскости частного положения,
записать их названия.
а) б)
D
2
E
2
A
2
A
1
B
1
E
1
a
2
a
1
a
2
a
1
O
2
Г
2
O
1
В
2
М
2
С
2
А
1
А
2
С
1
В
1
N
1
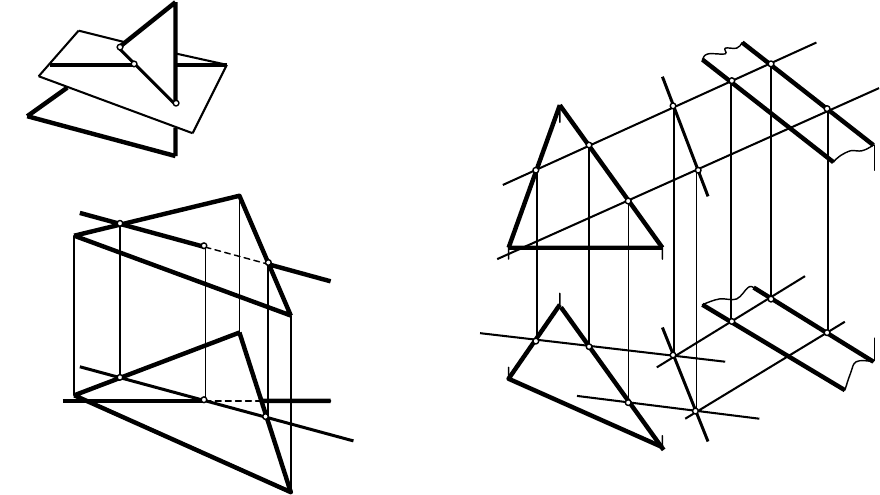
ОСНОВНЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ
Точка пересечения прямой с плоскостью определяется как точка,
принадлежащая одновременно и прямой, и плоскости. Если плоскость
занимает частное положение, то одна из проекций искомой точки находится
как точка пересечения проекции плоскости, выродившейся в прямую, с
одноимённой проекцией прямой. Остальные проекции находятся с помощью
линий связи. Если прямая
и плоскость имеют общее положение (рис. 5), то
для построения точки пересечения необходимо:
1. Провести через данную прямую a вспомогательную секущую плоскость
Г частного положения;
2. Построить линию b пересечения вспомогательной плоскости Г с
заданной плоскостью Σ;
3. Построить точку К пересечения прямых a и b.
Линия пересечения двух плоскостей является
прямой, одновременно
принадлежащей обеим пересекающимся плоскостям. Если одна из двух
пересекающихся плоскостей занимает частное положение, то одна
проекция искомой линии пересечения совпадает с проекцией плоскости,
выродившейся в прямую линию. Другая проекция строится исходя из условия
принадлежности прямой линии плоскости. Если обе плоскости занимают
общее положение, то для построения двух точек,
определяющих искомую
прямую, применяется метод вспомогательных секущих плоскостей. Любая
точка М искомой линии пересечения рассматривается как результат
пересечения двух прямых a и b, которые, в свою очередь, являются результатом
пересечения вспомогательной плоскости частного положения Г с заданными
плоскостями Σ и Т (рис. 6).
Рис. 5 Рис. 6
a
1
b
1
K
1
K
2
a
2
≡
Г
2
≡ b
2
a
b
K
Σ
Г
Г
2
≡ a
2
≡ b
2
1
2
2
2
1
1
2
1
a
1
b
1
3
2
4
2
M
2
4
1
M
1
3
2
