Насыров А.М. Волновые процессы. Электромагнитные волны в линиях передач
Подождите немного. Документ загружается.

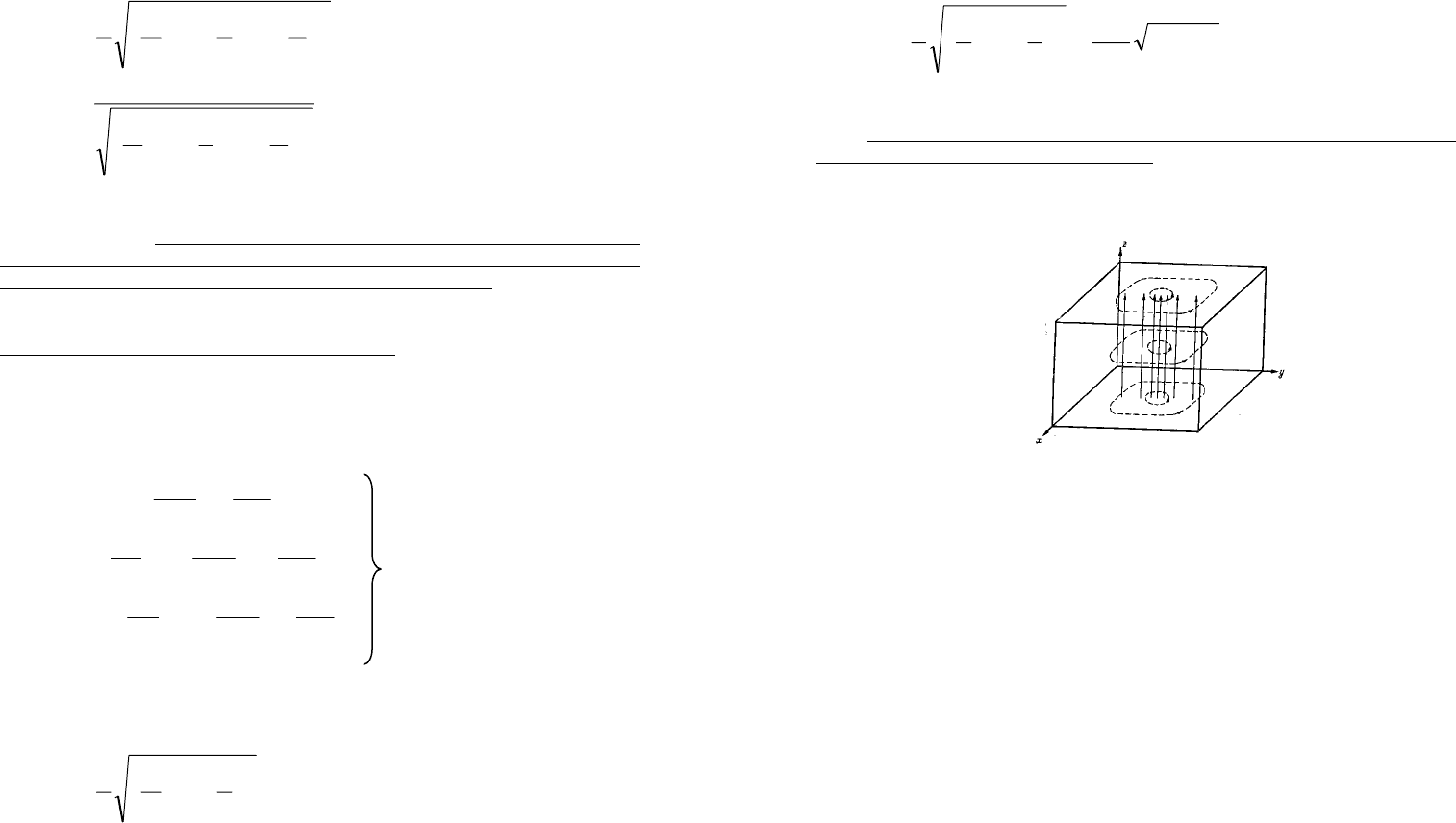
21
ɂɡ (3.4), (3.5), (3.7) ɫɥɟɞɭɟɬ, ɱɬɨ ɤɚɠɞɨɣ ɬɪɨɣɤɟ ɱɢɫɟɥ m, n, p ɫɨɨɬɜɟɬɫɬɜɭɟɬ
ɫɨɛɫɬɜɟɧɧɨɟ ɤɨɥɟɛɚɧɢɟ, ɢɦɟɸɳɟɟ ɫɨɛɫɬɜɟɧɧɭɸ ɱɚɫɬɨɬɭ f ɢ ɫɨɛɫɬɜɟɧɧɭɸ
ɞɥɢɧɭ ɜɨɥɧɵ Ȝ:
222
2
¸
¹
·
¨
©
§
+
¸
¹
·
¨
©
§
+
¸
¹
·
¨
©
§
=
l
p
b
n
a
mc
f (3.8)
222
2
¸
¹
·
¨
©
§
+
¸
¹
·
¨
©
§
+
¸
¹
·
¨
©
§
=
l
p
b
n
a
m
h
(3.9)
ȿɫɥɢ ɫɪɟɞɢ ɱɢɫɟɥ m, n, p ɧɟɬ ɧɭɥɟɣ, ɬɨ ɬɚɤɨɣ ɬɪɨɣɤɟ ɫɨɨɬɜɟɬɫɬɜɭɸɬ ɞɜɚ
ɫɨɛɫɬɜɟɧɧɵɯ ɤɨɥɟɛɚɧɢɹ ɫ ɨɞɧɨɣ ɢ ɬɨɣ ɠɟ ɱɚɫɬɨɬɨɣ, ɧɨ ɫ ɪɚɡɥɢɱɧɨɣ
ɫɬɪɭɤɬɭɪɨɣ ɩɨɥɹ. ȿɫɥɢ ɫɨɛɫɬɜɟɧɧɨɣ ɱɚɫɬɨɬɟ ɫɨɨɬɜɟɬɫɬɜɭɸɬ ɞɜɚ ɢɥɢ ɛɨɥɟɟ
ɫɨɛɫɬɜɟɧɧɵɯ ɤɨɥɟɛɚɧɢɹ, ɬɨ ɝɨɜɨɪɹɬ ɨ ɧɚɥɢɱɢɢ ɜɵɪɨɠɞɟɧɢɹ, ɢ ɞɚɧɧɚɹ
ɫɨɛɫɬɜɟɧɧɚɹ ɱɚɫɬɨɬɚ ɧɚɡɵɜɚɟɬɫɹ ɜɵɪɨɠɞɟɧɧɨɣ ɢɥɢ ɤɪɚɬɧɨɣ.
ɂɧɞɟɤɫɵ m, n, p ɨɩɪɟɞɟɥɹɸɬ ɧɚɩɪɚɜɥɟɧɢɹ ɪɚɫɩɪɨɫɬɪɚɧɟɧɢɹ ɩɥɨɫɤɢɯ
ɜɨɥɧ, ɧɚ ɤɨɬɨɪɵɟ ɪɚɡɥɚɝɚɟɬɫɹ ɩɨɥɟ ɫɨɛɫɬɜɟɧɧɵɯ ɤɨɥɟɛɚɧɢɣ ɪɟɡɨɧɚɬɨɪɚ.
Ⱦɜɭɤɪɚɬɧɨɟ ɜɵɪɨɠɞɟɧɢɟ ɫɨɛɫɬɜɟɧɧɵɯ ɱɚɫɬɨɬ,
ɨ ɤɨɬɨɪɨɦ ɝɨɜɨɪɢɥɨɫɶ ɜɵɲɟ,
ɮɢɡɢɱɟɫɤɢ ɫɜɹɡɚɧɨ ɫ ɬɟɦ, ɱɬɨ ɩɪɢ ɞɚɧɧɨɦ ɧɚɩɪɚɜɥɟɧɢɢ ɪɚɫɩɪɨɫɬɪɚɧɟɧɢɹ
ɩɥɨɫɤɨɣ ɜɨɥɧɵ ɟɺ ɩɨɥɹɪɢɡɚɰɢɹ ɦɨɠɟɬ ɛɵɬɶ ɩɪɨɢɡɜɨɥɶɧɨɣ.
Ɉɫɨɛɨɟ ɩɨɥɨɠɟɧɢɟ ɡɚɧɢɦɚɸɬ ɫɨɛɫɬɜɟɧɧɵɟ ɤɨɥɟɛɚɧɢɹ, ɭ ɤɨɬɨɪɵɯ ɨɞɢɧ
ɢɡ ɢɧɞɟɤɫɨɜ ɪɚɜɟɧ ɧɭɥɸ. Ⱦɥɹ ɩɪɢɦɟɪɚ, ɬɪɨɣɤɟ ɱɢɫɟɥ m, n, p ɫɨɨɬɜɟɬɫɬɜɭɟɬ
ɷɥɟɤɬɪɨɦɚɝɧɢɬɧɨɟ ɩɨɥɟ
b
yn
Sin
a
xm
ɋSinE
z
/
/
=
b
yn
Cos
a
xm
CSin
ikb
n
H
x
/
/
/
= (3.10)
b
yn
Sin
a
xm
CCos
ika
m
H
y
/
/
/
<=
0===
zyx
HEE
ȿɫɥɢ ɜ ɧɨɥɶ ɨɛɪɚɳɚɸɬɫɹ ɞɜɚ ɢɧɞɟɤɫɚ, ɬɨ ɩɨɥɟ ɬɨɠɞɟɫɬɜɟɧɧɨ ɢɫɱɟɡɚɟɬ.
Ɍɚɤɢɟ ɬɪɨɣɤɢ ɢɧɞɟɤɫɨɜ ɫɨɛɫɬɜɟɧɧɵɯ ɤɨɥɟɛɚɧɢɣ ɧɟ ɞɚɸɬ. ɋɨɝɥɚɫɧɨ (1.10)
ɩɨɥɟ ɢɦɟɟɬ ɫɨɛɫɬɜɟɧɧɭɸ ɱɚɫɬɨɬɭ:
22
2
¸
¹
·
¨
©
§
+
¸
¹
·
¨
©
§
=
b
n
a
mc
f (3.11)
22
ɉɪɨɫɬɟɣɲɟɟ ɤɨɥɟɛɚɧɢɟ ɜ ɩɨɥɨɫɬɢ ɩɨɥɭɱɚɟɬɫɹ ɩɪɢ ɡɧɚɱɟɧɢɢ
ɤɨɷɮɮɢɰɢɟɧɬɨɜ m=1, n=1, p=0. ɷɬɨ ɤɨɥɟɛɚɧɢɟ ɨɛɨɡɧɚɱɚɸɬ 110. ɉɪɢ ɭɫɥɨɜɢɢ
ɚ>
l, b >l ɨɧɨ ɢɦɟɟɬ ɱɚɫɬɨɬɭ:
22
22
2
11
2
ba
ab
ɫ
ba
c
f +=
¸
¹
·
¨
©
§
+
¸
¹
·
¨
©
§
= (3.12)
ɗɬɚ ɱɚɫɬɨɬɚ ɛɭɞɟɬ ɧɚɢɦɟɧɶɲɟɣ ɫɪɟɞɢ ɜɫɟɯ ɱɚɫɬɨɬ, ɨɩɪɟɞɟɥɹɟɦɵɯ
ɮɨɪɦɭɥɨɣ (3.8).
Ʉɨɥɟɛɚɧɢɟ ɪɟɡɨɧɚɬɨɪɚ ɧɚɡɵɜɚɸɬɫɹ ɨɫɧɨɜɧɵɦ ɤɨɥɟɛɚɧɢɟɦ, ɟɫɥɢ ɨɧɨ
ɢɦɟɟɬ ɧɚɢɧɢɡɲɭɸ ɫɨɛɫɬɜɟɧɧɭɸ ɱɚɫɬɨɬɭ.
Ʉɨɥɟɛɚɧɢɟ 110 ɹɜɥɹɟɬɫɹ ɨɫɧɨɜɧɵɦ ɤɨɥɟɛɚɧɢɟɦ ɩɪɹɦɨɭɝɨɥɶɧɨɝɨ
ɪɟɡɨɧɚɬɨɪɚ. ɋɬɪɭɤɬɭɪɚ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ
E
r
ɷɬɨɝɨ ɤɨɥɟɛɚɧɢɹ ɩɪɢɜɟɞɟɧɚ
ɧɚ Ɋɢɫ. 9.
_________
E
r
,
-------------
H
r
Ɋɢɫ.9
ɗɥɟɤɬɪɢɱɟɫɤɢɟ ɫɢɥɨɜɵɟ ɥɢɧɢɢ ɨɛɪɚɡɭɸɬ ɩɭɱɨɤ ɩɪɹɦɵɯ ɩɚɪɚɥɥɟɥɶɧɵɯ
ɨɫɢ z. ɉɭɱɨɤ ɧɚɢɛɨɥɟɟ ɝɭɫɬɨɣ ɩɪɢ
2/,2/ byax == . Ɇɚɝɧɢɬɧɵɟ ɫɢɥɨɜɵɟ
ɥɢɧɢɢ ɨɯɜɚɬɵɜɚɸɬ ɷɬɨɬ ɩɭɱɨɤ ɡɚɦɤɧɭɬɵɦɢ ɤɨɥɶɰɚɦɢ. Ʉɨɥɟɛɚɧɢɹ 110
ɧɚɡɵɜɚɸɬ ɤɨɥɟɛɚɧɢɹɦɢ
110
E .
4. ȼɨɥɧɵ ɬɢɩɨɜ ȿ ɢ ɇ ɜ ɜɨɥɧɨɜɨɞɚɯ ɤɪɭɝɥɨɝɨ ɫɟɱɟɧɢɹ
ȼɜɟɞɟɦ ɰɢɥɢɧɞɪɢɱɟɫɤɭɸ ɫɢɫɬɟɦɭ ɤɨɨɪɞɢɧɚɬ
),,( zr
, ɩɪɢɜɟɞɟɧɧɭɸ
ɧɚ Ɋɢɫ. 10.
23
Ɋɢɫ.10
ȼ ɷɬɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ ɭɪɚɜɧɟɧɢɹ ɞɥɹ ɤɨɦɩɨɧɟɧɬ
z
E ɢ
z
ɇ ɢɦɟɸɬ ɜɢɞ:
0
11
2
2
2
22
2
=+
,
,
+
,
,
+
,
,
zc
zzz
Ek
E
rr
E
rr
ȿ
(4.1)
0
11
2
2
2
22
2
=+
,
,
+
,
,
+
,
,
zc
zzz
Hk
H
rr
H
rr
H
, (4.2)
ɝɞɟ
µ_¡ta
~
22
+=
c
k .
Ɉɫɬɚɥɶɧɵɟ ɤɨɦɩɨɧɟɧɬɵ ɨɩɪɟɞɟɥɹɸɬɫɹ ɢɡ ɭɪɚɜɧɟɧɢɣ:
¸
¸
¹
·
¨
¨
©
§
,
,
+
,
,
+
<=
tµ
a
`a
zz
r
H
r
i
r
E
E
0
2
1
2
1
(4.3)
¸
¸
¹
·
¨
¨
©
§
,
,
+
,
,
<
+
<=
r
H
i
E
r
E
z
a
z
tµ
a
`a
2
1
2
1
(4.4)
¸
¸
¹
·
¨
¨
©
§
,
,
<
,
,
+
=
r
HE
r
i
ɇ
zz
r
a
¡t
`a
~
1
2
1
2
(4.5)
¸
¸
¹
·
¨
¨
©
§
,
,
+
,
,
+
<=
a
¡t
`a
zz
H
rr
E
i
ɇ
~
1
2
1
2
(4.6)
Ɂɞɟɫɶ ,ik+=
_
a
_
-ɤɨɷɮɮɢɰɢɟɧɬ ɩɨɝɥɨɳɟɧɢɹ, k -ɜɨɥɧɨɜɨɟ ɱɢɫɥɨ.
a
µ¡t`
~
22
1
= .
4.1. ȼɨɥɧɵ ɬɢɩɚ ȿ
()
0,0 &=
zz
EH ɜ ɜɨɥɧɨɜɨɞɚɯ ɤɪɭɝɥɨɝɨ ɫɟɱɟɧɢɹ
ɍɪɚɜɧɟɧɢɟ (4.1) ɜ ɱɚɫɬɧɵɯ ɩɪɨɢɡɜɨɞɧɵɯ ɪɟɲɚɟɬɫɹ ɦɟɬɨɞɨɦ ɪɚɡɞɟɥɟɧɢɹ
ɩɟɪɟɦɟɧɧɵɯ, ɬ.ɟ. ɩɭɬɟɦ ɩɪɟɞɫɬɚɜɥɟɧɢɹ
z
E ɜ ɜɢɞɟ:
a
z
z
RFeE
<
= , (4.7)
24
ɝɞɟ
R
- ɮɭɧɤɰɢɹ ɩɟɪɟɦɟɧɧɨɣ r: )(rRR = ;
F
-ɮɭɧɤɰɢɹ ɩɟɪɟɦɟɧɧɨɣ
:
)(
FF = . ɉɨɞɫɬɚɜɥɹɹ (4.7) ɜ (4.1) ɩɨɥɭɱɚɟɦ:
0
2
2
=+
vv
+
v
+
vv
RFk
r
RF
r
FR
FR
c
(4.8)
ɉɪɟɨɛɪɚɡɭɟɦ (4.8) ɬɚɤɢɦ ɨɛɪɚɡɨɦ, ɱɬɨɛɵ ɱɥɟɧɵ, ɡɚɜɢɫɹɳɢɟ ɨɬ
r
ɢ
ɧɚɯɨɞɢɥɢɫɶ ɜ ɪɚɡɧɵɯ ɱɚɫɬɹɯ ɭɪɚɜɧɟɧɢɹ:
F
F
rk
R
R
r
R
R
r
c
vv
<=+
v
+
vv
222
(4.9)
ȼ (4.8) ɢ (4.9)
R
v
ɢ
R
vv
-ɩɟɪɜɚɹ ɢ ɜɬɨɪɚɹ ɩɪɨɢɡɜɨɞɧɵɟ ɮɭɧɤɰɢɢ
R
ɩɨ
ɩɟɪɟɦɟɧɧɨɣ
r
.
F
v
ɢ
F
vv
-ɩɟɪɜɚɹ ɢ ɜɬɨɪɚɹ ɩɪɨɢɡɜɨɞɧɵɟ ɮɭɧɤɰɢɢ
F
ɩɨ
ɩɟɪɟɦɟɧɧɨɣ
. ɉɪɢɪɚɜɧɹɟɦ ɥɟɜɵɟ ɢ ɩɪɚɜɵɟ ɱɚɫɬɢ ɭɪɚɜɧɟɧɢɹ (4.9) ɤ ɨɞɧɨɣ ɢ
ɬɨɣ ɠɟ ɜɟɥɢɱɢɧɟ
2
m :
0
2
=+
vv
FmF (4.10)
0
1
2
2
2
=
¸
¸
¹
·
¨
¨
©
§
<+
v
+
vv
R
r
m
kR
r
R
c
(4.11)
Ɋɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ (4.10) ɢɦɟɟɬ ɜɢɞ:
A
F
=
Sinm
Cosm
(4.12)
Ɏɭɧɤɰɢɹ
F
ɞɨɥɠɧɚ ɢɦɟɬɶ ɨɞɧɨ ɢ ɬɨɠɟ ɡɧɚɱɟɧɢɟ ɩɪɢ
.3600
0
==
ɢ ɗɬɨ ɜɨɡɦɨɠɧɨ, ɟɫɥɢ m - ɰɟɥɨɟ ɱɢɫɥɨ ɢɥɢ ɧɭɥɶ.
Ȼɟɡɪɚɡɥɢɱɧɨ, ɤɚɤ ɜɵɪɚɡɢɬɶ ɮɭɧɤɰɢɸ
F
, ɱɟɪɟɡ
Cosm ɢɥɢ
Sinm . Ɂɚɦɟɧɚ
ɪɚɜɧɨɫɢɥɶɧɚ ɢɡɦɟɧɟɧɢɸ ɧɚɱɚɥɚ ɨɬɫɱɟɬɚ
ɧɚ 90
0
. Ⱦɚɥɟɟ ɜɫɸɞɭ ɛɭɞɟɦ
ɜɵɪɚɠɚɬɶ ɮɭɧɤɰɢɸ
F
ɱɟɪɟɡ
Cosm .
ɍɪɚɜɧɟɧɢɟ (4.11) ɢɦɟɟɬ ɪɟɲɟɧɢɟ:
)( rkBJR
cm
= , (4.13)
ɝɞɟ
)( rkJ
cm
- ɮɭɧɤɰɢɹ Ȼɟɫɫɟɥɹ ɜɬɨɪɨɝɨ ɪɨɞɚ.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ:
a
z
cmz
eCosmrkJEE
<
= )(
0
(4.14)
ɉɨɞɫɬɚɜɥɹɹ ɜ ɭɪɚɜɧɟɧɢɟ (4.3)-(4.6)
0=
z
H ɢ ɜɦɟɫɬɨ
z
E ɟɝɨ ɡɧɚɱɟɧɢɟ ɢɡ
(4.14), ɢɦɟɟɦ:
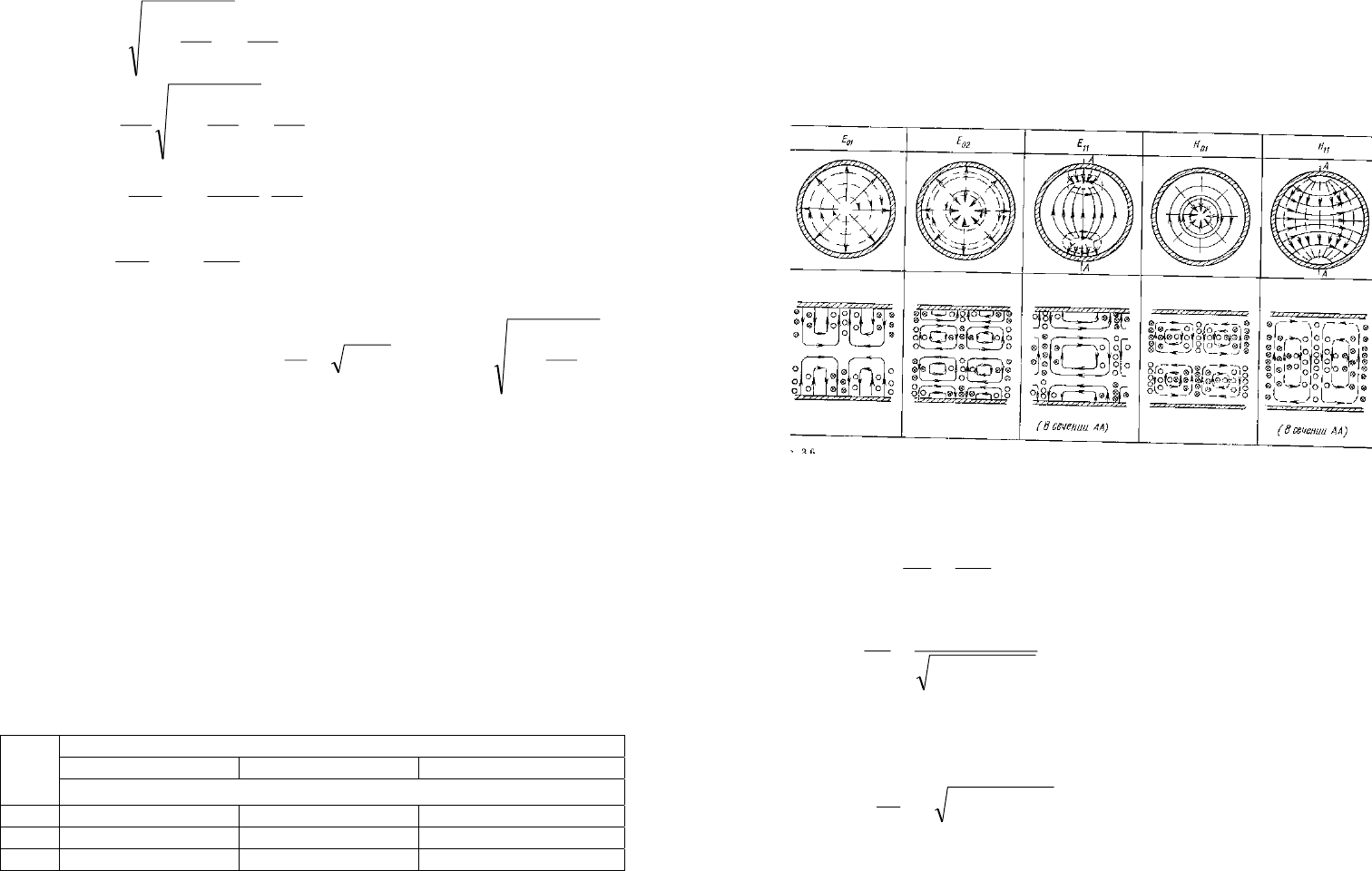
25
a
h
h
h
h
z
cm
kp
ɤɪ
r
eCosmrkJEiE
<
v
u
¸
¸
¹
·
¨
¨
©
§
<<= )(1
0
2
(4.15)
a
h
h
h
h
z
cm
kp
ɤɪc
eSinmrkJE
rk
m
iE
<
u
¸
¸
¹
·
¨
¨
©
§
<= )(1
0
2
(4.16)
a
h
h
z
cm
ɤɪ
BcCE
r
eSinmrkJE
rzk
m
i
z
E
H
<
u<=<= )(
0
(4.17)
a
h
h
z
cm
B
ɤɪ
CE
r
eCosmrkJE
z
i
z
E
H
<
v
u<== )(
0
(4.18)
ȼ ɷɬɢɯ ɭɪɚɜɧɟɧɢɹɯ:
2
1,,/2
¸
¸
¹
·
¨
¨
©
§
<=====
ɤɪ
BCEaaɫɌȿɆCEcɤɪ
zz
H
E
zzk
h
h
¡µ/h
(4.19)
ȿɫɥɢ ɫɬɟɧɤɢ ɜɨɥɧɨɜɨɞɚ ɜɵɩɨɥɧɟɧɵ ɢɡ ɢɞɟɚɥɶɧɨɝɨ ɩɪɨɜɨɞɧɢɤɚ (ɬ. ɟ. ɢɯ
ɭɞɟɥɶɧɚɹ ɩɪɨɜɨɞɢɦɨɫɬɶ
'A
m
), ɬɨ ɜɵɩɨɥɧɹɟɬɫɹ ɝɪɚɧɢɱɧɨɟ ɭɫɥɨɜɢɟ
0=
o
E , ɝɞɟ
o
E -ɤɚɫɚɬɟɥɶɧɚɹ (ɬɚɧɝɟɧɰɢɚɥɶɧɚɹ) ɫɨɫɬɚɜɥɹɸɳɚɹ ɜɟɤɬɨɪɚ
E
r
.
ɉɪɢ ɫɨɛɥɸɞɟɧɢɢ ɷɬɨɝɨ ɭɫɥɨɜɢɹ ɢɡ (4.14) ɫɥɟɞɭɟɬ ɪɚɜɟɧɫɬɜɨ, ɢɡ ɤɨɬɨɪɨɝɨ
ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ
c
k :
0)(
=akJ
cm
(4.20)
Ɏɭɧɤɰɢɹ Ȼɟɫɫɟɥɹ ɨɛɪɚɳɚɟɬɫɹ ɜ ɧɭɥɶ ɩɪɢ ɛɟɫɤɨɧɟɱɧɨ ɛɨɥɶɲɨɦ ɱɢɫɥɟ
ɡɧɚɱɟɧɢɣ ɚɪɝɭɦɟɧɬɚ. ɗɬɨ ɬɚɤ ɧɚɡɵɜɚɟɦɵɟ ɤɨɪɧɢ ɮɭɧɤɰɢɢ Ȼɟɫɫɟɥɹ. ȼ ɬɚɛɥɢɰɟ
1 ɩɪɢɜɟɞɟɧɵ ɤɨɪɧɢ
P
mn
ɮɭɧɤɰɢɢ Ȼɟɫɫɟɥɹ ɞɥɹ ɧɟɤɨɬɨɪɵɯ ɡɧɚɱɟɧɢɣ m ɢ n.
Ɍɚɛɥɢɰɚ 1.
m
n
1 2 3
P
mn
0 2,405 5,52 8,654
1 3,832 7,016 10,173
5,136 8,417 11,620
26
Ʉɚɠɞɨɦɭ ɡɧɚɱɟɧɢɸ P
mn
ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɫɜɨɟ ɡɧɚɱɟɧɢɟ aPk
mnc
/= . Ʉɚɠɞɨɦɭ
ɡɧɚɱɟɧɢɸ m ɢ n ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɨɩɪɟɞɟɥɟɧɧɚɹ ɫɬɪɭɤɬɭɪɚ ɩɨɥɹ ɜ ɜɨɥɧɨɜɨɞɟ. Ⱦɥɹ
ɜɨɥɧ ɬɢɩɚ
01
E ,
02
E ɢ
11
E ɫɬɪɭɤɬɭɪɚ ɩɨɥɹ ɜ ɜɨɥɧɨɜɨɞɟ ɤɪɭɝɥɨɝɨ ɫɟɱɟɧɢɹ
ɩɪɢɜɟɞɟɧɚ ɧɚ Ɋɢɫ. 11.
Ɋɢɫ.11
Ʉɪɢɬɢɱɟɫɤɚɹ ɞɥɢɧɚ ɜɨɥɧɵ ɬɢɩɚ
E
ɨɩɪɟɞɟɥɹɟɬɫɹ ɢɡ ɭɪɚɜɧɟɧɢɹ
mnc
ɤɪȿ
P
a
k
mn
/
/
h
22
== (4.21)
Ɏɚɡɨɜɚɹ ɫɤɨɪɨɫɬɶ ɪɚɫɩɪɨɫɬɪɚɧɟɧɢɹ ɜɨɥɧɵ ɪɚɜɧɚ:
()
2
/1
ɤɪ
E
c
k
v
hh
t
<
==
(4.22)
Ɂɞɟɫɶ ɋ ñ ɫɤɨɪɨɫɬɶ ɷɥɟɤɬɪɨɦɚɝɧɢɬɧɨɣ ɜɨɥɧɵ ɜ ɜɚɤɭɭɦɟ,
h
- ɞɥɢɧɚ ɜɨɥɧɵ
ɌȿɆ ɜ ɫɪɟɞɟ ɛɟɡ ɩɨɬɟɪɶ ɫ ɩɚɪɚɦɟɬɪɚɦɢ
a
¡
ɢ
a
µ
. ɋɤɨɪɨɫɬɶ ɪɚɫɩɪɨɫɬɪɚɧɟɧɢɹ
ɷɧɟɪɝɢɢ:
()
2
2
/1
ɤɪɗ
c
v
ɫ
v
hh
<== (4.23)
Ɂɧɚɱɟɧɢɹ ɤɪɢɬɢɱɟɫɤɢɯ ɞɥɢɧ ɞɥɹ ɜɨɥɧ ɬɢɩɚ ȿ ɩɪɢ ɪɚɡɥɢɱɧɵɯ ɡɧɚɱɟɧɢɹɯ m ɢ n
ɩɪɢɜɟɞɟɧɵ ɜ ɬɚɛɥɢɰɟ 2.
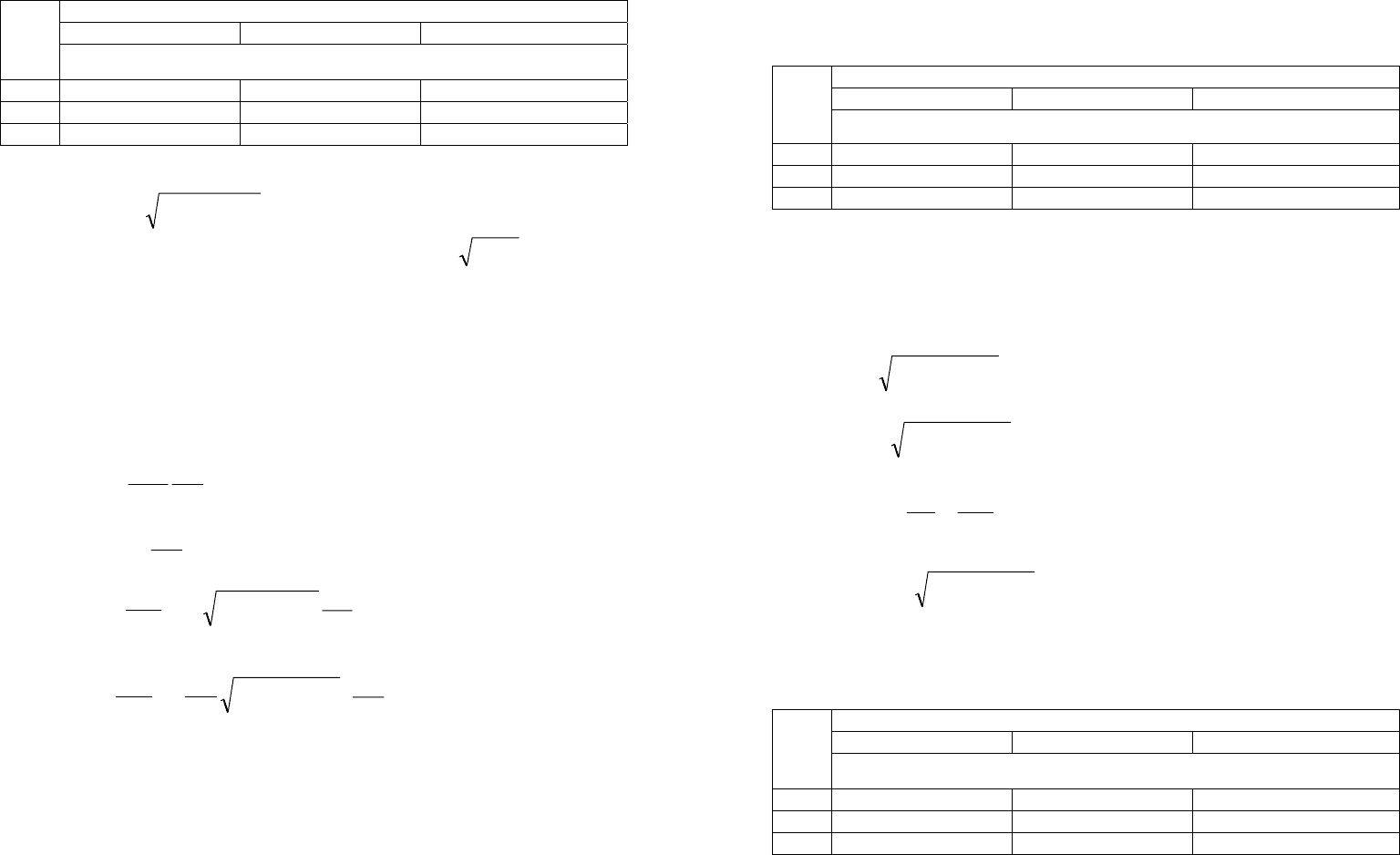
27
Ɍɚɛɥɢɰɚ 2.
m
n
1 2 3
aE
mnɤɪ
/
h
0 2,61 1,14 0,725
1 1,64 0,895 0,62
2 1,22 0,745 0,54
ȼɨɥɧɨɜɵɟ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɜɨɥɧ ɬɢɩɚ ȿ ɪɚɜɧɵ:
()
2
/1
ɤɪBCE
zz
hh
<= (4.24)
B
z - ɜɨɥɧɨɜɨɟ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɞɥɹ ɜɨɥɧ ɬɢɩɚ ɌȿɆ:
ɚɚB
z
¡µ
= .
4.2. ȼɨɥɧɵ ɬɢɩɚ ɇ
()
0,0 =&
zz
EH ɜ ɜɨɥɧɨɜɨɞɚɯ ɤɪɭɝɥɨɝɨ ɫɟɱɟɧɢɹ
Ⱥɧɚɥɢɡ ɫɬɪɭɤɬɭɪɵ ɩɨɥɹ ɜɨɥɧ ɬɢɩɚ ɇ ɩɨɞɨɛɟɧ ɚɧɚɥɢɡɭ ɫɬɪɭɤɬɭɪɵ ɩɨɥɹ
ɜɨɥɧɵ ɬɢɩɚ ȿ. ɂɫɩɨɥɶɡɭɸɬɫɹ ɭɪɚɜɧɟɧɢɹ (4.2)-(4.6), ɜ ɤɨɬɨɪɵɯ ɩɨɥɚɝɚɸɬ
0=
z
E . ȼɵɪɚɠɟɧɢɟ ɞɥɹ ɫɨɫɬɚɜɥɹɸɳɢɯ ɩɨɥɹ ɜɨɥɧ ɬɢɩɚ ɇ ɩɨɥɭɱɚɸɬɫɹ
ɫɥɟɞɭɸɳɢɦɢ:
a
z
cmz
eCosmrkJHH
<
= )(
0
(4.25)
a
h
h
z
cm
ɤp
c
B
r
eSinmrkJH
rk
mz
iE
<
u= )(
0
(4.26)
a
h
h
z
cm
ɤp
B
eCosmrkJHizE
<
u= )(
0
(4.27)
()
a
h
h
hh
z
cm
ɤɪ
ɤɪ
CH
r
eCosmrkJHi
z
E
H
<
v
<<=<=
)(/1
0
2
(4.28)
()
a
h
h
hh
z
cm
ɤɪ
ɤɪ
cCH
r
eSinmrkJH
rk
m
i
z
E
H
<
u<== )(/1
0
2
(4.29)
Ⱦɥɹ ɨɩɪɟɞɟɥɟɧɢɹ ɫɬɪɭɤɬɭɪɵ ɩɨɥɹ ɜ ɜɨɥɧɨɜɨɞɟ ɢɫɩɨɥɶɡɭɟɦ ɭɪɚɜɧɟɧɢɹ,
ɩɨɥɭɱɚɸɳɢɟɫɹ ɢɡ ɭɫɥɨɜɢɹ ɪɚɜɟɧɫɬɜɚ ɧɭɥɸ ɫɨɫɬɚɜɥɹɸɳɟɣ
E ɧɚ
ɩɨɜɟɪɯɧɨɫɬɢ ɜɨɥɧɨɜɨɞɚ. ɂɡ (4.27) ɫɥɟɞɭɟɬ:
0)( =
v
akJ
cm
(4.30)
28
ɍɪɚɜɧɟɧɢɟ (4.30) ɢɦɟɟɬ ɛɟɫɤɨɧɟɱɧɨɟ ɱɢɫɥɨ ɤɨɪɧɟɣ. Ɉɛɨɡɧɚɱɢɦ ɢɯ ɱɟɪɟɡ
mn
P
v
.
ȼ ɬɚɛɥɢɰɟ ɩɪɢɜɟɞɟɧɵ
mn
P
v
ɞɥɹ ɪɚɡɥɢɱɧɵɯ ɡɧɚɱɟɧɢɣ m ɢ n.
Ɍɚɛɥɢɰɚ 3.
m
n
1 2 3
mn
P
v
0 3,832 7,016 10,174
1 1,841 5,332 8,536
2 3,054 6,705 9,965
Ʉɚɠɞɨɦɭ ɡɧɚɱɟɧɢɸ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɨɩɪɟɞɟɥɟɧɧɚɹ ɫɬɪɭɤɬɭɪɚ
ɷɥɟɤɬɪɨɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ. Ⱦɥɹ ɜɨɥɧ ɬɢɩɚ
01
H ɢ
11
H ɫɬɪɭɤɬɭɪɚ
ɷɥɟɤɬɪɨɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɩɪɢɜɟɞɟɧɚ ɧɚ Ɋɢɫ. 11.
Ɏɚɡɨɜɚɹ ɫɤɨɪɨɫɬɶ ɪɚɫɩɪɨɫɬɪɚɧɟɧɢɹ ɜɨɥɧɵ ɬɢɩɚ
H
ɪɚɜɧɚ:
()
2
/1
ɤɪ
cv
hh
<= (4.31)
ɋɤɨɪɨɫɬɶ ɪɚɫɩɪɨɫɬɪɚɧɟɧɢɹ ɷɧɟɪɝɢɢ:
()
2
/1
ɤɪɗ
cv
hh
<= (4.32)
Ʉɪɢɬɢɱɟɫɤɚɹ ɫɭɦɦɚ ɜɨɥɧɵ
mnc
ɤɪH
P
a
k
mn
v
==
/
/
h
22
(4.33)
ȼɨɥɧɨɜɨɟ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɜɨɥɧ ɬɢɩɚ ɇ:
()
2
/1
ɤɪBCH
zz
hh
<= (4.34)
ȼ ɬɚɛɥɢɰɟ 4 ɩɪɢɜɟɞɟɧɵ ɡɧɚɱɟɧɢɹ
ɤɪ
h
ɞɥɹ ɜɨɥɧ ɬɢɩɚ ɇ ɩɪɢ ɪɚɡɥɢɱɧɵɯ
ɡɧɚɱɟɧɢɹɯ m ɢ n.
Ɍɚɛɥɢɰɚ 4.
m
n
1 2 3
aH
mnɤɪ
/
h
0 1,64 0,895 0,62
1 3,41 1,18 0,736
2 2,06 0,935 0,63
29
ɂɡ ɬɚɛɥɢɰ ɜɢɞɧɨ, ɱɬɨ ɫɚɦɭɸ ɧɢɡɤɭɸ ɱɚɫɬɨɬɭ ɜ ɜɨɥɧɨɜɨɞɚɯ ɤɪɭɝɥɨɝɨ
ɫɟɱɟɧɢɹ ɢɦɟɟɬ ɜɨɥɧɚ ɬɢɩɚ
11
H . ɋɬɪɭɤɬɭɪɚ ɩɨɥɹ ɷɬɨɣ ɜɨɥɧɵ ɛɥɢɡɤɚ ɤ
ɫɬɪɭɤɬɭɪɟ ɩɨɥɹ ɜɨɥɧɵ
10
H ɜ ɜɨɥɧɨɜɨɞɟ ɤɪɭɝɥɨɝɨ ɫɟɱɟɧɢɹ. ɉɪɢ ɡɚɞɚɧɧɨɣ
ɞɥɢɧɟ ɜɨɥɧɵ
h
ɪɚɫɩɪɨɫɬɪɚɧɟɧɢɟ ɷɧɟɪɝɢɢ ɜ ɜɨɥɧɨɜɨɞɟ ɤɪɭɝɥɨɝɨ ɫɟɱɟɧɢɹ
ɜɨɡɦɨɠɧɨ, ɟɫɥɢ ɟɝɨ ɪɚɞɢɭɫ ɛɨɥɶɲɟ
hh
93,041,3/
min
==G
5. ɗɥɟɤɬɪɨɦɚɝɧɢɬɧɵɟ ɜɨɥɧɵ ɜ ɤɨɚɤɫɢɚɥɶɧɨɣ ɥɢɧɢɢ
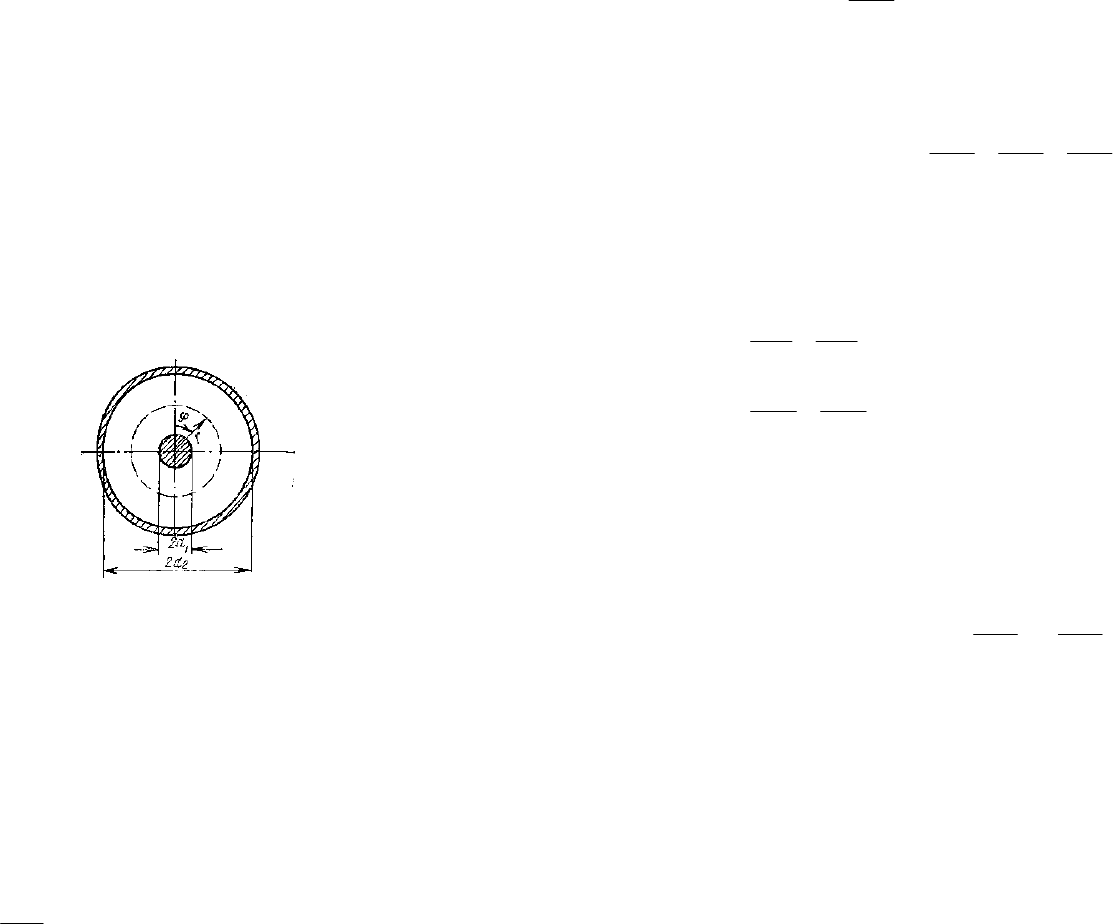
ɋɯɟɦɚ ɤɨɚɤɫɢɚɥɶɧɨɣ ɥɢɧɢɢ ɩɪɢɜɟɞɟɧɚ ɧɚ Ɋɢɫ.12. Ʌɢɧɢɹ ɫɨɫɬɨɢɬ ɢɡ
ɜɧɭɬɪɟɧɧɟɝɨ ɩɪɨɜɨɞɧɢɤɚ ɪɚɞɢɭɫɨɦ
1
a ɢ ɜɧɟɲɧɟɝɨ ɩɪɨɜɨɞɧɢɤɚ (ɷɤɪɚɧɚ) ɫ
ɜɧɭɬɪɟɧɧɢɦ ɪɚɞɢɭɫɨɦ
2
a . Ɇɟɠɞɭ ɩɪɨɜɨɞɧɢɤɚɦɢ ɦɨɠɟɬ ɧɚɯɨɞɢɬɶɫɹ ɜɨɡɞɭɯ
ɢɥɢ ɤɚɤɨɣ-ɥɢɛɨ ɞɢɷɥɟɤɬɪɢɤ.
Ɋɢɫ.12.
ȼ ɤɨɚɤɫɢɚɥɶɧɨɣ ɥɢɧɢɢ ɩɨ ɜɧɭɬɪɟɧɧɟɦɭ ɩɪɨɜɨɞɧɢɤɭ ɦɨɠɟɬ ɬɟɱɶ ɬɨɤ
ɩɪɨɜɨɞɢɦɨɫɬɢ. ɉɨɷɬɨɦɭ ɜɨɡɦɨɠɧɨ ɪɚɫɩɪɨɫɬɪɚɧɟɧɢɟ ɜɨɥɧ ɬɢɩɚ ɌȿɆ. Ɍɚɤɠɟ
ɦɨɝɭɬ ɪɚɫɩɪɨɫɬɪɚɧɹɬɶɫɹ ɜɨɥɧɵ ɬɢɩɨɜ ȿ ɢ ɇ ɡɚ ɫɱɟɬ ɬɨɝɨ, ɱɬɨ ɜɧɭɬɪɢ ɷɤɪɚɧɚ
ɦɨɝɭɬ ɪɚɫɩɪɨɫɬɪɚɧɹɬɶɫɹ, ɫɨɜɟɪɲɚɹ ´ ɫɤɚɱɤɢª, ɩɚɪɰɢɚɥɶɧɵɟ ɜɨɥɧɵ.
5.1 ȼɨɥɧɵ ɬɢɩɚ ɌȿɆ ɜ ɤɨɚɤɫɢɚɥɶɧɨɣ ɥɢɧɢɢ
Ⱦɥɹ ɝɚɪɦɨɧɢɱɟɫɤɢɯ ɤɨɥɟɛɚɧɢɣ ɜ ɨɛɥɚɫɬɢ, ɝɞɟ ɨɬɫɭɬɫɬɜɭɸɬ ɫɬɨɪɨɧɧɢɟ
ɷɥɟɤɬɪɢɱɟɫɤɢɟ ɦɚɝɧɢɬɧɵɟ ɬɨɤɢ ɢ ɡɚɪɹɞɵ, ɜɨɥɧɨɜɵɟ ɭɪɚɜɧɟɧɢɹ ɞɥɹ
ȿ
r
ɢ
H
r
ɩɨɥɟɣ ɨɩɢɫɵɜɚɸɬɫɹ ɭɪɚɜɧɟɧɢɹɦɢ Ƚɟɥɶɦɝɨɥɶɰɚ:
E
t
E
E
aa
r
r
r
µ¡tµ¡
~~
2
2
2
<=
,
,
=6 (5.1)
30
H
t
H
H
aa
r
r
r
µ¡tµ¡
~~
2
2
2
<=
,
,
=6 (5.2)
<6 ɨɩɟɪɚɬɨɪ Ʌɚɩɥɚɫɚ. Ⱦɥɹ ɜɟɤɬɨɪɧɵɯ ɮɭɧɤɰɢɣ:
ArotrotAgraddivA
rrr
<=6 (5.3)
Ⱦɥɹ ɫɤɚɥɹɪɧɵɯ ɮɭɧɤɰɢɣ:
2
2
2
2
2
2
zyx
divgrad
,
^,
+
,
^,
+
,
^,
=^=6^
(5.4)
ɍɫɥɨɜɢɟɦ ɫɭɳɟɫɬɜɨɜɚɧɢɹ ɜɨɥɧ ɬɢɩɚ ɌȿɆ, ɭ ɤɨɬɨɪɵɯ
0==
zz
HE , ɹɜɥɹɟɬɫɹ
ɜɵɩɨɥɧɟɧɢɟ ɪɚɜɟɧɫɬɜɚ:
0
~
222
=+=
ac
k
µ¡ta
(5.5)
ɋ ɭɱɟɬɨɦ (5.5) ɢɡ (5.1) ɢ (5.2) ɫɥɟɞɭɟɬ:
0
2
2
2
2
=
,
,
+
,
,
y
E
x
E
r
r
(5.6)
2
2
2
2
y
H
x
H
,
,
+
,
,
r
r
=0 (5.7)
ɍɪɚɜɧɟɧɢɹ (5.6) ɢ (5.7) ɨɩɪɟɞɟɥɹɸɬ ɫɬɪɭɤɬɭɪɭ ɩɨɥɹ ɜɨɥɧ ɬɢɩɚ ɌȿɆ ɢ
ɩɪɟɞɫɬɚɜɥɹɸɬ ɞɜɭɦɟɪɧɵɟ ɭɪɚɜɧɟɧɢɹ Ʌɚɩɥɚɫɚ. ɉɨɥɹ, ɭɞɨɜɥɟɬɜɨɪɹɸɳɢɟ
ɭɪɚɜɧɟɧɢɹɦ Ʌɚɩɥɚɫɚ, ɹɜɥɹɸɬɫɹ ɩɨɬɟɧɰɢɚɥɶɧɵɦɢ. ɂɡ (5.6) ɢ (5.7) ɫɥɟɞɭɟɬ, ɱɬɨ
ɩɨɥɹ ɜ ɩɨɩɟɪɟɱɧɨɦ ɫɟɱɟɧɢɢ ɤɨɚɤɫɢɚɥɶɧɨɣ ɥɢɧɢɢ ɩɨɬɟɧɰɢɚɥɶɧɵ. ɗɬɨ
ɩɨɡɜɨɥɹɟɬ ɪɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ (5.6) ɞɥɹ
ȿ
r
ɜɵɪɚɡɢɬɶ ɱɟɪɟɡ ɝɪɚɞɢɟɧɬ ɮɭɧɤɰɢɢ
^
, ɧɚɡɵɜɚɟɦɨɣ ɫɤɚɥɹɪɧɵɦ ɩɨɬɟɧɰɢɚɥɨɦ [4]:
aa
zz
e
y
j
x
iegradE
<<
¸
¸
¹
·
¨
¨
©
§
,
^,
+
,
^,
<=^<=
rr
r
(5.8)
Ɂɞɟɫɶ
ji
r
r
,- ɨɪɬɵ ɜɞɨɥɶ ɤɨɨɪɞɢɧɚɬɧɵɯ ɨɫɟɣ. Ⱥɧɚɥɨɝɢɱɧɨɟ ɜɵɪɚɠɟɧɢɟ ɦɨɠɧɨ
ɡɚɩɢɫɚɬɶ ɢ ɞɥɹ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ
H
r
.
ȼ ɭɪɚɜɧɟɧɢɹ (5.6) (5.7) ɧɟ ɜɯɨɞɢɬ ɱɚɫɬɨɬɚ. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɞɥɹ ɜɨɥɧ
ɌȿɆ ɫɬɪɭɤɬɭɪɚ ɩɨɥɹ ɜ ɩɨɩɟɪɟɱɧɨɣ ɩɥɨɫɤɨɫɬɢ ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɱɚɫɬɨɬɵ.
ɍɪɚɜɧɟɧɢɟ Ɇɚɤɫɜɟɥɥɚ ɜ ɫɥɭɱɚɟ ɝɚɪɦɨɧɢɱɟɫɤɢɯ ɩɨɥɟɣ ɢɦɟɟɬ ɜɢɞ:
HiErot
a
r
r
tµ
<= (5.9)
EiHrot
r
r
¡t
~
= (5.10)
ɂɡ ɷɬɢɯ ɭɪɚɜɧɟɧɢɣ ɜ ɫɥɭɱɚɟ
0==
zz
HE (ɜɨɥɧɚ ɬɢɩɚ ɌȿɆ) ɩɨɥɭɱɚɟɦ:

31
¡t
a
~
i
H
E
y
x
<= (5.11)
¡t
a
~
i
H
E
x
y
= (5.12)
ȿɫɥɢ ɫɩɪɨɟɤɬɢɪɨɜɚɬɶ ɭɪɚɜɧɟɧɢɟ (5.10) ɧɚ ɨɫɶ Z ɢ ɩɨɞɫɬɚɜɢɬɶ ɜɦɟɫɬɨ
y
H ɢ
x
H ɢɯ ɜɵɪɚɠɟɧɢɹ ɢɡ (5.11) ɢ (5.12), ɩɨɥɭɱɢɦ:
0=
,
,
+
,
,
y
E
x
E
y
x
(5.13)
ɉɨɞɫɬɚɜɥɹɹ ɜ (5.13) ɜɦɟɫɬɨ
x
E ɢ
y
E ɢɯ ɜɵɪɚɠɟɧɢɹ ɢɡ (5.8) ɩɨɥɭɱɚɟɦ ɞɥɹ
ɫɤɚɥɹɪɧɨɝɨ ɩɨɬɟɧɰɢɚɥɚ:
0
2
2
2
2
=
,
^,
+
,
^,
yx
(5.14)
Ɍ.ɟ. ɫɤɚɥɹɪɧɵɣ ɩɨɬɟɧɰɢɚɥ ɭɞɨɜɥɟɬɜɨɪɹɟɬ ɭɪɚɜɧɟɧɢɸ Ʌɚɩɥɚɫɚ. ȼ
ɰɢɥɢɧɞɪɢɱɟɫɤɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ
z
r
,,
ɭɪɚɜɧɟɧɢɟ (5.14) ɩɪɢɧɢɦɚɟɬ
ɜɢɞ:
0
11
2
2
22
2
=
,
^,
u+
,
^,
u+
,
^,
rrrr
(5.15)
ȼ ɫɢɥɭ ɨɫɟɜɨɣ ɫɢɦɦɟɬɪɢɢ
^
ɧɟ ɡɚɜɢɫɢɬ ɨɬ
, ɩɨɷɬɨɦɭ
,
^
,
=0. ɍɪɚɜɧɟɧɢɟ
(5.15) ɩɪɢɧɢɦɚɟɬ ɜɢɞ:
0
1
2
2
=
,
^,
u+
,
^,
r
r
r
(5.16)
Ɋɟɲɟɧɢɟɦ ɷɬɨɝɨ ɭɪɚɜɧɟɧɢɹ ɹɜɥɹɟɬɫɹ:
B
r
A +<=
^
ln , ɝɞɟ Ⱥ ɢ ȼ ɤɨɧɫɬɚɧɬɵ. (5.17)
ɇɚɩɪɹɠɟɧɧɨɫɬɶ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ:
a
a
aa
z
m
z
zz
r
e
r
a
E
r
Ae
e
r
ergradEE
<
<
<<
==
,
^,
<=^<==
1
, (5.18)
ɝɞɟ
1
a - ɪɚɞɢɭɫ ɜɧɭɬɪɟɧɧɟɝɨ ɩɪɨɜɨɞɧɢɤɚ ɤɨɚɤɫɢɚɥɶɧɨɣ ɥɢɧɢɢ,
m
E - ɧɚɩɪɹɠɟɧɧɨɫɬɶ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ ɧɚ ɟɝɨ ɩɨɜɟɪɯɧɨɫɬɢ )(
1
ar = .
ɇɚɩɪɹɠɟɧɧɨɫɬɶ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɨɩɪɟɞɟɥɹɟɬɫɹ ɜɵɪɚɠɟɧɢɟɦ:
32
a
µ
¡
z
a
a
m
B
r
e
r
a
E
z
E
HH
<
===
1
(5.19)
ɋɬɪɭɤɬɭɪɚ ɩɨɥɹ ɜɨɥɧɵ ɌȿɆ ɜ ɤɨɚɤɫɢɚɥɶɧɨɣ ɥɢɧɢɢ ɩɨɤɚɡɚɧɚ ɧɚ Ɋɢɫ. 13.
Ɋɢɫ.13
ȼɨɥɧɨɜɨɟ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɤɨɚɤɫɢɚɥɶɧɨɣ ɥɢɧɢɢ ɪɚɜɧɨ:
IUZ
ȼ
/= (5.20)
ɝɞɟ U ɢ I - ɧɚɩɪɹɠɟɧɢɟ ɬɨɤ ɜ ɥɢɧɢɢ.
a
z
m
a
a
m
a
a
r
e
a
a
Eadr
r
a
EdrEU
<
³³
===
1
2
1
1
ln
2
1
2
1
(5.21)
Ɂɞɟɫɶ
2
a - ɜɧɭɬɪɟɧɧɢɣ ɪɚɞɢɭɫ ɷɤɪɚɧɚ ɤɨɚɤɫɢɚɥɶɧɨɣ ɥɢɧɢɢ. Ɍɨɤ, ɬɟɤɭɳɢɣ ɜ
ɤɨɚɤɫɢɚɥɶɧɨɣ ɥɢɧɢɢ, ɪɚɜɟɧ ɥɢɧɟɣɧɨɦɭ ɢɧɬɟɝɪɚɥɭ ɨɬ ɧɚɩɪɹɠɟɧɧɨɫɬɢ
ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɩɨ ɡɚɦɤɧɭɬɨɦɭ ɤɨɧɬɭɪɭ, ɨɤɪɭɠɚɸɳɟɦɭ ɜɧɭɬɪɟɧɧɢɣ
ɩɪɨɜɨɞɧɢɤ.
a
/
/
z
mm
eɇadaHI
<
==
³
11
2
0
2 (5.22)
ɡɞɟɫɶ
m
ɇ ñ ɧɚɩɪɹɠɟɧɧɨɫɬɶ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɭ ɩɨɜɟɪɯɧɨɫɬɢ ɜɧɭɬɪɟɧɧɟɝɨ
ɩɪɨɜɨɞɧɢɤɚ
)/(
Bmm
zɇE = .
ȼɨɥɧɨɜɨɟ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɤɨɚɤɫɢɚɥɶɧɨɣ ɥɢɧɢɢ
1
2
ln
2
1
a
a
I
U
Z
a
a
ȼɅ
¡
µ
/
== (5.23)
ȼ ɥɢɧɢɢ, ɡɚɩɨɥɧɟɧɧɨɣ ɜɨɡɞɭɯɨɦ,
Ɉɦ
aa
/¡µ
120/ = . ȼɨɥɧɨɜɨɟ
ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɬɚɤɨɣ ɥɢɧɢɢ ɪɚɜɧɨ:
33
1
2
ln60
a
a
Z
ȼ
= (5.24).
ȼ ɥɢɧɢɢ, ɡɚɩɨɥɧɟɧɧɨɣ ɞɢɷɥɟɤɬɪɢɤɨɦ ɫ ɨɬɧɨɫɢɬɟɥɶɧɨɣ ɞɢɷɥɟɤɬɪɢɱɟɫɤɨɣ
ɩɪɨɧɢɰɚɟɦɨɫɬɶɸ
¡
:
1
2
ln
60
a
a
Z
ȼ
¡
= (5.25)
5.2 ȼɨɥɧɵ ɬɢɩɨɜ ȿ ɢ ɇ ɜ ɤɨɚɤɫɢɚɥɶɧɨɣ ɥɢɧɢɢ.
ȼɨɥɧɨɜɵɟ ɭɪɚɜɧɟɧɢɹ ɞɥɹ ɧɚɯɨɠɞɟɧɢɹ
z
E ɢ
z
H ɫɨɫɬɚɜɥɹɸɳɢɯ ɩɨɥɹ
ɢɦɟɸɬ ɜɢɞ:
0
2
2
2
2
2
=+
,
,
+
,
,
zc
zz
Ek
y
E
x
E
(5.26)
0
2
2
2
2
2
=+
,
,
+
,
,
zc
zz
Hk
y
H
x
H
(5.27)
ȼ ɰɢɥɢɧɞɪɢɱɟɫɤɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ ɷɬɢ ɭɪɚɜɧɟɧɢɹ ɢɦɟɸɬ ɜɢɞ:
0
11
2
2
2
22
2
=+
,
,
u+
,
,
u+
,
,
zc
zzz
Ek
E
rr
E
rr
E
(5.28)
0
11
2
2
2
22
2
=+
,
,
u+
,
,
u+
,
,
zc
zzz
Hk
H
rr
H
rr
H
(5.29)
ɋɨɫɬɚɜɥɹɸɳɢɟ
z
E ɢ
z
ɇ ɨɩɪɟɞɟɥɹɸɬɫɹ ɢɡ ɭɪɚɜɧɟɧɢɣ (5.26) ɢ (5.27).
Ɉɫɬɚɥɶɧɵɟ ɫɨɫɬɚɜɥɹɸɳɢɟ ɨɩɪɟɞɟɥɹɸɬɫɹ ɢɡ ɭɪɚɜɧɟɧɢɣ:
¸
¸
¹
·
¨
¨
©
§
,
,
u+
,
,
+
<=
tµ
a
`a
z
a
z
r
H
r
i
r
E
ȿ
2
1
2
1
(5.30)
¸
¸
¹
·
¨
¨
©
§
,
,
u+
,
,
<
+
=
r
H
i
E
r
ȿ
z
a
z
tµ
a
`a
2
1
2
1
(5.31)
¸
¸
¹
·
¨
¨
©
§
,
,
u<
,
,
+
=
r
HE
r
i
H
zz
r
a
¡t
`a
~
1
2
1
2
(5.32)
¸
¸
¹
·
¨
¨
©
§
,
,
u+
,
,
+
<=
a
¡t
`a
H
rr
E
iH
z
~
1
2
1
2
(5.33)
34
ȼɨɥɧɵ ɬɢɩɚ ȿ )0,0( =&
zz
HE
ȼ ɭɪɚɜɧɟɧɢɹɯ (5.30)-(5.33) ɧɭɠɧɨ ɩɨɥɨɠɢɬɶ 0=
z
H . ɋɨɫɬɚɜɥɹɸɳɚɹ
z
E ɨɩɪɟɞɟɥɹɟɬɫɹ ɢɡ ɭɪɚɜɧɟɧɢɹ (5.28) ɍɪɚɜɧɟɧɢɹ ɞɥɹ ɫɨɫɬɚɜɥɹɸɳɢɯ ɩɨɥɹ
ɩɪɢɨɛɪɟɬɚɸɬ ɜɢɞ:
r
E
ȿ
z
r
,
,
u
+
<=
2
1
2
`a
a
(5.34)
`a
a
,
,
u
+
<=
z
E
r
ȿ
1
2
1
2
(5.35)
`a
¡
t
,
,
u
+
=
z
r
E
r
i
H
1
~
2
1
2
(5.36)
r
Ei
H
z
,
,
u
+
<=
2
1
2
~
`a
¡
t
(5.37)
Ɋɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ (5.28) ɢɦɟɟɬ ɜɢɞ:
a
z
cmz
eCosmrkzEE
<
= )(
0
(5.38)
ɝɞɟ
m
z - ɮɭɧɤɰɢɹ Ȼɟɫɫɟɥɹ, ɇɟɣɦɚɧɚ ɢɥɢ ɏɚɧɤɟɥɹ. ȼ ɫɥɭɱɚɟ ɤɨɚɤɫɢɚɥɶɧɨɣ
ɥɢɧɢɢ ɜɫɸɞɭ ɜ ɢɫɫɥɟɞɭɟɦɨɣ ɨɛɥɚɫɬɢ ɩɨɥɟ ɦɟɠɞɭ ɜɧɭɬɪɟɧɧɢɦ ɩɪɨɜɨɞɧɢɤɨɦ ɢ
ɷɤɪɚɧɨɦ
r ɨɬɥɢɱɧɨ ɨɬ ɧɭɥɹ. ɉɨɷɬɨɦɭ ɩɨɥɧɨɟ ɪɟɲɟɧɢɟ ɞɨɥɠɧɨ ɫɨɞɟɪɠɚɬɶ
ɮɭɧɤɰɢɢ Ȼɟɫɫɟɥɹ ɢ ɇɟɣɦɚɧɚ. Ɏɭɧɤɰɢɸ ɏɚɧɤɟɥɹ ɦɨɠɧɨ ɢɫɤɥɸɱɢɬɶ, ɬ.ɤ. ɨɧɚ
ɜɵɪɚɠɚɟɬɫɹ ɱɟɪɟɡ ɮɭɧɤɰɢɢ Ȼɟɫɫɟɥɹ ɢ ɇɟɣɦɚɧɚ. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɪɟɲɟɧɢɟ
ɭɪɚɜɧɟɧɢɹ (5.30) ɩɪɟɞɫɬɚɜɥɹɟɬɫɹ ɜ ɜɢɞɟ:
[]
a
z
cmcmz
eCosmrkBNrkAJE
<
+= )()( (5.39)
ɝɞɟ
)( rkJ
cm
- ɮɭɧɤɰɢɹ Ȼɟɫɫɟɥɹ ɩɟɪɜɨɝɨ ɪɨɞɚ m- ɝɨ ɩɨɪɹɞɤɚ,
)( rkN
cm
-ɮɭɧɤɰɢɹ ɇɟɣɦɚɧɚ m-ɝɨ ɩɨɪɹɞɤɚ,
Ⱥ, ȼ ñ ɩɨɫɬɨɹɧɧɵɟ.
ɍ ɩɨɜɟɪɯɧɨɫɬɢ ɜɧɭɬɪɟɧɧɟɝɨ ɢ ɜɧɟɲɧɟɝɨ ɩɪɨɜɨɞɧɢɤɚ
z
E ɪɚɜɧɨ ɧɭɥɸ.
Ɉɬɫɸɞɚ ɫɥɟɞɭɟɬ:
0)()(
0)()(
22
11
=+
=+
akBNakAJ
akBNakAJ
cmcm
cmcm
(5.40)
ɂɡ ɷɬɨɣ ɫɢɫɬɟɦɵ ɫɥɟɞɭɟɬ:
)(
)(
)(
)(
2
1
2
1
akN
akN
akJ
akJ
cm
cm
cm
cm
= (5.41)
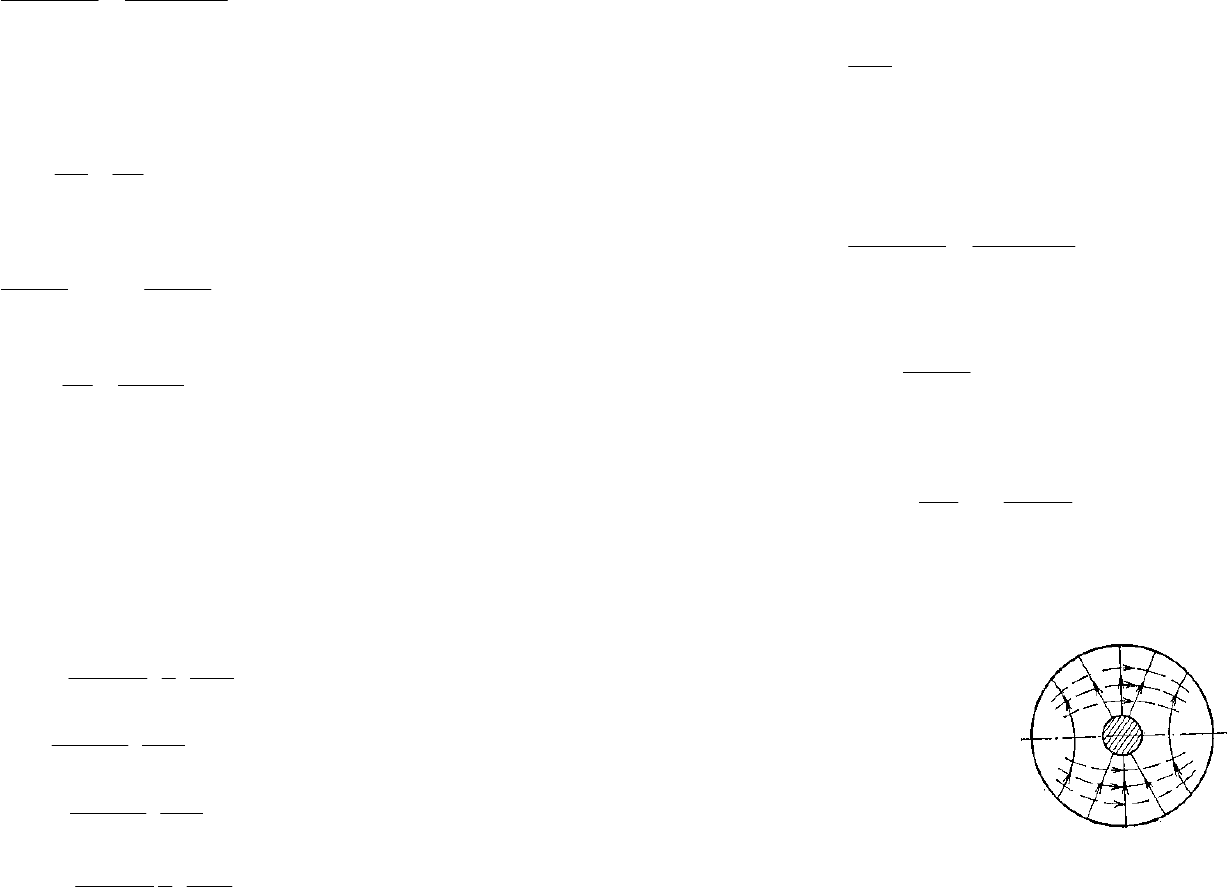
35
Ɉɛɨɡɧɚɱɢɦ
12
/ aab = . Ɍɨɝɞɚ ɭɪɚɜɧɟɧɢɟ (5.41) ɩɪɢɧɢɦɚɟɬ ɜɢɞ:
)(
)(
)(
)(
1
1
1
1
abkN
akN
abkJ
akJ
cm
cm
cm
cm
= (5.42)
ɍɪɚɜɧɟɧɢɟ (5.42) ɢɦɟɟɬ ɛɟɫɤɨɧɟɱɧɨɟ ɦɧɨɠɟɫɬɜɨ ɤɨɪɧɟɣ, ɤɚɠɞɵɣ ɢɡ ɤɨɬɨɪɵɯ
ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɨɩɪɟɞɟɥɟɧɧɨɣ ɤɪɢɬɢɱɟɫɤɨɣ ɞɥɢɧɟ ɜɨɥɧɵ. Ɇɚɤɫɢɦɚɥɶɧɚɹ
ɤɪɢɬɢɱɟɫɤɚɹ ɞɥɢɧɚ ɜɨɥɧɵ ɜ ɥɢɧɢɢ ɨɩɪɟɞɟɥɹɟɬɫɹ ɦɢɧɢɦɚɥɶɧɵɦ
ɡɧɚɱɟɧɢɟɦ
c
k .
cɤɪ
ɤɪ
kf
ɫ
/
h
2
== (5.43)
ɂɫɫɥɟɞɨɜɚɧɢɟ (5.42) ɩɨɤɚɡɵɜɚɟɬ, ɱɬɨ ɦɢɧɢɦɚɥɶɧɨɟ ɡɧɚɱɟɧɢɟ ɢɦɟɟɬ ɩɟɪɜɵɣ
ɤɨɪɟɧɶ (n=1), ɩɨɥɭɱɚɸɳɢɣɫɹ ɩɪɢ m=0 [2]. ɗɬɨɬ ɤɨɪɟɧɶ ɥɟɠɢɬ ɜ ɩɪɟɞɟɥɚɯ
,
3
12
1
01
12
1
aa
a
P
aa
a
<
>>
<
/
ɟɫɥɢ 1>> bz
ɉɪɚɤɬɢɱɟɫɤɢɟ ɡɧɚɱɟɧɢɹ
b ɧɟ ɜɵɯɨɞɹɬ ɢɡ ɷɬɢɯ ɩɪɟɞɟɥɨɜ. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ,
121
01
01
aaa
P
k
C
<
5=
/
ɉɨɞɫɬɚɜɥɹɹ
ɤɪC
k
h/
/2
01
= , ɩɨɥɭɱɚɟɦ
)(2
12
aa
ɤɪ
<5
h
(5.44)
ȼɨɥɧɵ ɬɢɩɚ
)0,0( &=
zzz
HEH
ɋɨɫɬɚɜɥɹɸɳɭɸ
z
H ɨɩɪɟɞɟɥɢɦ ɢɡ ɭɪɚɜɧɟɧɢɹ (5.29). ȼ ɫɥɭɱɚɟ
0=
z
E ɨɫɬɚɥɶɧɵɟ ɫɨɫɬɚɜɥɹɸɳɢɟ ɩɨɥɭɱɚɸɬɫɹ ɢɡ ɭɪɚɜɧɟɧɢɣ (5.30)-(5.33):
`a
t
µ
,
,
uu
+
<=
z
a
r
H
r
i
ȿ
1
2
1
2
(5.45)
r
Hi
ȿ
za
,
,
u
+
=
2
1
2
`a
t
µ
(5.46)
r
H
H
z
r
,
,
u
+
<=
2
1
2
`a
a
(5.47)
`a
a
,
,
u
+
<=
H
r
H
1
2
1
2
(5.48)
36
Ɋɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ (5.29) ɢɦɟɟɬ ɜɢɞ:
[]
a
z
cmcmz
eCosmrkDNrkCJH
<
+= )()( (5.49)
ɉɪɢ
1
ar = ɢ
2
ar = ɤɨɦɩɨɧɟɧɬɚ 0=
E .
[]
a
z
cmcmc
z
eCosmrkNDrkJCk
r
H
<
v
+
v
=
,
,
)()( (5.50)
Ɉɬɫɸɞɚ ɫɥɟɞɭɟɬ:
0)()(
0)()(
22
11
=
v
+
v
=
v
+
v
akNDakJC
akNDakJ
ɋ
cmcm
cmcm
(5.51)
ɂɥɢ
)(
)(
)(
)(
1
1
1
1
abkN
akN
abkJ
akJ
cm
cm
cm
cm
v
v
=
v
v
,
12
/ aab = (5.52)
ɂɫɫɥɟɞɨɜɚɧɢɹ ɭɪɚɜɧɟɧɢɹ (5.52) ɩɨɤɚɡɵɜɚɸɬ, ɱɬɨ ɨɧɨ ɢɦɟɟɬ ɛɟɫɤɨɧɟɱɧɨɟ
ɦɧɨɠɟɫɬɜɨ ɤɨɪɧɟɣ
mn
P
v
. Ʉɨɪɧɢ ɩɪɢɛɥɢɠɟɧɧɨ ɪɚɜɧɵ [2]:
21
1
1
2
aa
ma
P
m
+
5
v
(5.53)
ɋɨɨɬɜɟɬɫɬɜɟɧɧɨ
)/(2/
21111
aamaPk
mcm
+=
v
=
.
Ɉɬɫɸɞɚ ɤɪɢɬɢɱɟɫɤɚɹ ɞɥɢɧɚ ɜɨɥɧɵ
m
aa
k
cm
ɤɪm
21
1
1
2
+
==
/
/
h
(5.54)
ɋɚɦɚɹ ɞɥɢɧɧɚɹ ɤɪɢɬɢɱɟɫɤɚɹ ɜɨɥɧɚ ɩɨɥɭɱɚɟɬɫɹ ɩɪɢ m=1:
)(
2111
aa
ɤɪ
+==
/h
(5.55)
ɋɬɪɭɤɬɭɪɚ ɜɨɥɧɵ
11
H ɜ ɤɨɚɤɫɢɚɥɶɧɨɣ ɥɢɧɢɢ ɩɨɤɚɡɚɧɚ ɧɚ Ɋɢɫ.14.
Ɋɢɫ. 14
ɉɪɢ ɢɫɩɨɥɶɡɨɜɚɧɢɢ ɤɨɚɤɫɢɚɥɶɧɨɣ ɥɢɧɢɢ ɞɥɹ ɪɚɛɨɬɵ ɧɚ ɜɨɥɧɟ ɬɢɩɚ
ɌȿɆ ɧɟɨɛɯɨɞɢɦɨ, ɱɬɨɛɵ ɪɚɛɨɱɚɹ ɜɨɥɧɚ ɛɵɥɚ ɛɨɥɶɲɟ
)(
21
aa +
/
. ȼ
37
ɩɪɨɬɢɜɧɨɦ ɫɥɭɱɚɟ ɨɞɧɨɜɪɟɦɟɧɧɨ ɫ ɜɨɥɧɨɣ ɌȿɆ ɦɨɠɟɬ ɜɨɡɧɢɤɧɭɬɶ ɜɨɥɧɚ
11
H .
6. ɗɥɟɤɬɪɨɦɚɝɧɢɬɧɵɟ ɜɨɥɧɵ ɜ ɨɞɧɨɪɨɞɧɵɯ ɥɢɧɢɹɯ [1]
6.1. Ɍɟɥɟɝɪɚɮɧɵɟ ɭɪɚɜɧɟɧɢɹ
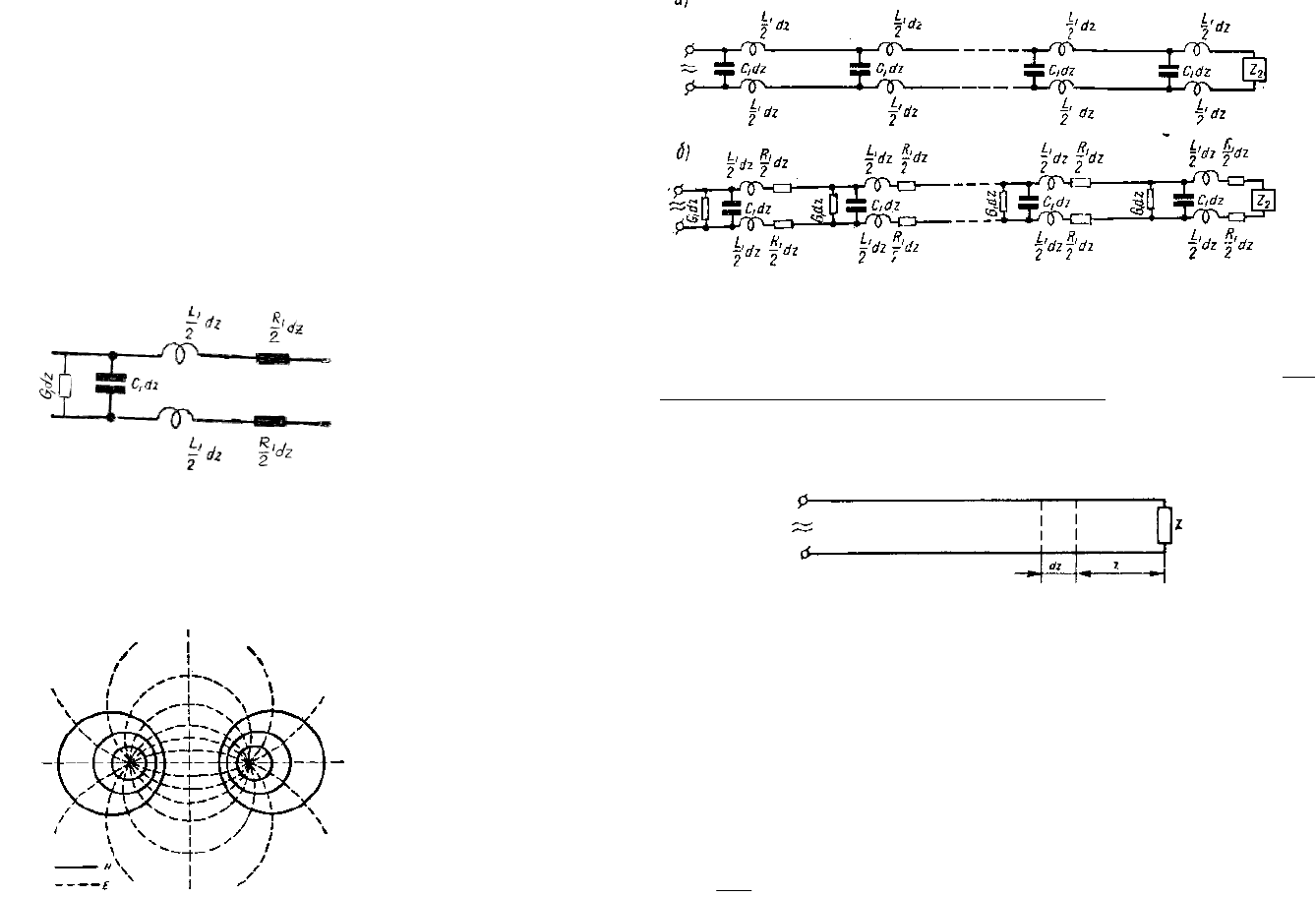
Ⱦɥɹ ɚɧɚɥɢɡɚ ɩɪɟɞɫɬɚɜɢɦ ɥɢɧɢɸ ɤɚɤ ɫɭɦɦɭ ɷɥɟɦɟɧɬɨɜ, ɫɨɫɬɨɹɳɢɯ ɢɡ
ɢɧɞɭɤɬɢɜɧɨɫɬɢ
1
L ɧɚ ɟɞɢɧɢɰɭ ɞɥɢɧɵ ɥɢɧɢɢ,
1
C - ɟɦɤɨɫɬɢ ɧɚ ɟɞɢɧɢɰɭ ɞɥɢɧɵ
ɥɢɧɢɢ,
1
R - ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɧɚ ɟɞɢɧɢɰɭ ɞɥɢɧɵ ɥɢɧɢɢ,
1
G - ɩɪɨɜɨɞɢɦɨɫɬɢ ɧɚ
ɟɞɢɧɢɰɭ ɞɥɢɧɵ ɥɢɧɢɢ. ɗɤɜɢɜɚɥɟɧɬɧɵɣ ɷɥɟɦɟɧɬ ɥɢɧɢɢ ɩɪɢɜɟɞɟɧ ɧɚ Ɋɢɫ.15.
Ɋɢɫ. 15
Ʉɚɠɞɵɣ ɷɥɟɦɟɧɬ ɥɢɧɢɢ ɹɜɥɹɟɬɫɹ ɧɨɫɢɬɟɥɟɦ ɤɚɤ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ, ɬɚɤ ɢ
ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɟɣ. ɇɚ Ɋɢɫ.16 ɩɪɢɜɟɞɟɧɚ ɤɚɪɬɢɧɚ ɪɚɫɩɪɟɞɟɥɟɧɢɹ
ɷɥɟɤɬɪɢɱɟɫɤɢɯ ɢ ɦɚɝɧɢɬɧɵɯ ɩɨɥɟɣ ɫɢɥɨɜɵɯ ɥɢɧɢɣ ɜ ɫɟɱɟɧɢɢ ɞɜɭɯɩɪɨɜɨɞɧɨɣ
ɥɢɧɢɢ.
Ɋɢɫ.16
Ʌɢɧɢɹ ɜ ɰɟɥɨɦ ɦɨɠɟɬ ɛɵɬɶ ɡɚɦɟɧɟɧɚ ɷɤɜɢɜɚɥɟɧɬɧɨɣ ɫɯɟɦɨɣ, ɫɨɫɬɨɹɳɟɣ ɢɡ
ɷɥɟɦɟɧɬɚɪɧɵɯ ɢɧɞɭɤɬɢɜɧɨɫɬɟɣ ɢ ɟɦɤɨɫɬɟɣ, ɩɨɤɚɡɚɧɧɨɣ ɧɚ Ɋɢɫ.17.
38
Ɋɢɫ.17
ɚ) - ɛɟɡ ɭɱɟɬɚ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɭɬɟɱɤɢ
ɛ) - ɫ ɭɱɟɬɨɦ ɫɨɩɪɨɬɢɜɥɟɧɢɹ ɭɬɟɱɤɢ
ɉɨɥɭɱɢɦ ɡɚɜɢɫɢɦɨɫɬɢ ɦɟɠɞɭ ɬɨɤɨɦ ɢ ɧɚɩɪɹɠɟɧɢɟɦ ɨɞɧɨɪɨɞɧɨɣ ɥɢɧɢɢ. ɗɬɢ
ɡɚɜɢɫɢɦɨɫɬɢ ɧɚɡɵɜɚɸɬ ɬɟɥɟɝɪɚɮɧɵɦɢ ɭɪɚɜɧɟɧɢɹɦɢ. Ⱦɥɹ ɜɵɜɨɞɚ ɭɪɚɜɧɟɧɢɣ
ɜɵɞɟɥɢɦ ɛɟɫɤɨɧɟɱɧɨ ɦɚɥɵɣ ɷɥɟɦɟɧɬ
dz ɧɚ ɪɚɫɫɬɨɹɧɢɢ
z
ɨɬ ɤɨɧɰɚ ɞɥɢɧɧɨɣ
ɥɢɧɢɢ. (Ɋɢɫ.18).
Ɋɢɫ.18
ȼɵɞɟɥɟɧɧɵɣ ɷɥɟɦɟɧɬ
dz ɨɛɥɚɞɚɟɬ ɛɟɫɤɨɧɟɱɧɨ ɦɚɥɵɦɢ ɢɧɞɭɤɬɢɜɧɨɫɬɶɸ dL ,
ɟɦɤɨɫɬɶɸ dC , ɫɨɩɪɨɬɢɜɥɟɧɢɟɦ dR ɢ ɩɪɨɜɨɞɢɦɨɫɬɶɸ dG . Ɉɧɢ ɪɚɜɧɵ:
.;;;
1111
dzGdGdzRdRdzCdCdzLdL ==== (6.1)
ɉɚɞɟɧɢɟ ɧɚɩɪɹɠɟɧɢɹ dU ɧɚ ɷɥɟɦɟɧɬɟ dz ɪɚɜɧɨ ɬɨɤɭ
I
, ɩɪɨɯɨɞɹɳɟɦɭ ɩɨ
ɧɟɦɭ, ɭɦɧɨɠɟɧɧɨɦɭ ɧɚ ɩɨɥɧɨɟ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɷɥɟɦɟɧɬɚ:
dzIZdzLiRdLidRIdU
111
)()( =+=+=
tt
(6.2)
ɝɞɟ
t
- ɭɝɥɨɜɚɹ ɱɚɫɬɨɬɚ ɧɚɩɪɹɠɟɧɢɹ, ɩɪɢɥɨɠɟɧɧɨɝɨ ɤ ɥɢɧɢɢ
111
LiRZ
t
+= . ɂɡ (6.2) ɫɥɟɞɭɟɬ:
1
IZ
d
z
dU
= (6.3)
ɂɡɦɟɧɟɧɢɟ ɬɨɤɚ
dI ɧɚ ɷɥɟɦɟɧɬɟ dz ɪɚɜɧɨ ɬɨɤɭ, ɨɬɜɟɬɜɥɹɸɳɟɦɭɫɹ ɜ ɟɦɤɨɫɬɶ
ɢ ɩɪɨɜɨɞɢɦɨɫɬɶ ɷɬɨɝɨ ɷɥɟɦɟɧɬɚ::
39
dzUYdzCiGUdCidGUdI
111
)()( =+=+=
tt
(6.4)
ɝɞɟ
111
CiGY
t
+= . Ⱦɟɥɹ ɨɛɟ ɱɚɫɬɢ ɭɪɚɜɧɟɧɢɹ ɧɚ dz , ɩɨɥɭɱɚɟɦ
1
UY
d
z
dI
= (6.5)
ɍɪɚɜɧɟɧɢɹ (6.3) ɢ (6.5) ɧɚɡɵɜɚɸɬɫɹ ɬɟɥɟɝɪɚɮɧɵɦɢ ɭɪɚɜɧɟɧɢɹɦɢ.
Ɋɟɲɟɧɢɟ ɬɟɥɟɝɪɚɮɧɵɯ ɭɪɚɜɧɟɧɢɣ
ɉɪɨɞɢɮɮɟɪɟɧɰɢɪɭɟɦ ɭɪɚɜɧɟɧɢɹ (6.3) ɢ (6.5) ɩɨ
z
.
d
z
dI
Z
d
z
Ud
1
2
2
= ,
d
z
dU
Y
d
z
Id
1
2
2
= (6.6)
ɉɨɞɫɬɚɜɥɹɹ ɜ (6.6) ɡɧɚɱɟɧɢɹ
d
z
dI
ɢ
d
z
dU
ɢɡ (6.3) ɢ (6.5) ɢ ɩɪɟɨɛɪɚɡɨɜɵɜɚɹ,
ɩɨɥɭɱɢɦ:
0
11
2
2
=< UZY
d
z
Ud
0
11
2
2
=< IZY
d
z
Id
(6.7)
Ⱦɢɮɮɟɪɟɧɰɢɚɥɶɧɵɟ ɭɪɚɜɧɟɧɢɹ ɢɦɟɸɬ ɪɟɲɟɧɢɹ:
aa
aa
zz
zz
eBeAI
eBeAU
<
<
+=
+=
22
11
(6.8)
ɝɞɟ
2121
,,, BBAA - ɩɨɫɬɨɹɧɧɵɟ ɢɧɬɟɝɪɢɪɨɜɚɧɢɹ.
ikCiGLiRYZ +=++==
_tta
))((
111111
, (6.9)
Ɂɞɟɫɶ
a
- ɤɨɷɮɮɢɰɢɟɧɬ ɪɚɫɩɪɨɫɬɪɚɧɟɧɢɹ ɜɨɥɧɵ,
_
- ɤɨɷɮɮɢɰɢɟɧɬ
ɡɚɬɭɯɚɧɢɹ,
k - ɜɨɥɧɨɜɨɟ ɱɢɫɥɨ.
ɉɨɞɫɬɚɜɢɦ (6.8) ɜ (6.3); ɩɨɥɭɱɢɦ:
)(
22111
aaaa
aa
zzzz
eBeAZeBeA
<<
+=< (6.10)
Ɋɚɜɟɧɫɬɜɨ (6.10) ɭɞɨɜɥɟɬɜɨɪɹɟɬɫɹ, ɟɫɥɢ ɜɵɩɨɥɧɟɧɵ ɭɫɥɨɜɢɹ:
211211
, BZBAZA =<=
aa
.
Ɉɬɫɸɞɚ ɫɥɟɞɭɟɬ:
ll
1
2
1
2
,
B
B
A
A <==
, (6.11)
ɝɞɟ ɜɜɟɞɟɧɨ ɨɛɨɡɧɚɱɟɧɢɟ
l
, ɧɚɡɵɜɚɟɦɨɟ ɜɨɥɧɨɜɵɦ ɫɨɩɪɨɬɢɜɥɟɧɢɟɦ ɥɢɧɢɢ.
40
11
11
1
1
CiG
LiR
Y
Z
t
t
l
+
+
==
, (6.12)
ɉɨɞɫɬɚɜɥɹɹ ɜ (6.8) ɫɨɨɬɧɨɲɟɧɢɟ (6.11), ɩɨɥɭɱɚɟɦ:
)(
1
11
11
aa
aa
l
zz
zz
eBeAI
eBeAU
<
<
<=
+=
(6.13)
Ɉɛɨɡɧɚɱɢɦ ɧɚɩɪɹɠɟɧɢɟ ɢ ɬɨɤ ɧɚ ɤɨɧɰɟ ɥɢɧɢɢ (ɜ ɬɨɱɤɟ Z=0) ɱɟɪɟɡ
2
U ɢ
2
I .
ɉɨɞɫɬɚɜɥɹɹ ɜ (6.13) Z=0 ɢ ɪɟɲɚɹ ɨɬɧɨɫɢɬɟɥɶɧɨ
11
,BA , ɢɦɟɟɦ:
)(
2
1
)(
2
1
221
221
l
l
IUB
IUA
<=
+=
(6.14)
ɉɨɞɫɬɚɜɥɹɹ ɜ (6.13) ɜɦɟɫɬɨ
11
, BA ɢɯ ɡɧɚɱɟɧɢɹ, ɩɪɢɜɨɞɢɦ ɷɬɢ ɭɪɚɜɧɟɧɢɹ ɤ
ɜɢɞɭ:
zsh
U
zchII
zshIzchUU
a
l
a
a
l
a
2
2
22
+=
+=
(6.15)
ȼ ɫɥɭɱɚɟ ɜɵɫɨɤɢɯ ɱɚɫɬɨɬ
1111
, GCRL >>>>
tt
, ɩɨɷɬɨɦɭ ɦɨɠɧɨ
ɫɱɢɬɚɬɶ ɩɪɢɛɥɢɠɟɧɧɨ ɜɨɥɧɨɜɨɟ ɫɨɩɪɨɬɢɜɥɟɧɢɟ ɥɢɧɢɢ ɪɚɜɧɵɦ
1
1
C
L
W =5
l
ȿɫɥɢ ɥɢɧɢɢ ɤɨɪɨɬɤɢɟ, ɦɨɠɧɨ ɩɪɟɞɩɨɥɨɠɢɬɶ, ɱɬɨ
0
11
== GR . ɉɪɢ ɷɬɨɦ
ik=
a
ɢ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɬɨɤɚ ɢ ɧɚɩɪɹɠɟɧɢɹ ɢɦɟɸɬ ɜɢɞ:
Sinkz
W
U
iCoskzII
SinkziICoskzUU
2
2
22
+=
+=
(6.16)
Ʌɢɧɢɹ ɛɟɡ ɩɨɬɟɪɶ ɧɚɡɵɜɚɟɬɫɹ ɢɞɟɚɥɶɧɨɣ ɥɢɧɢɟɣ.
6.2. Ʉɨɷɮɮɢɰɢɟɧɬ ɡɚɬɭɯɚɧɢɹ, ɤɨɷɮɮɢɰɢɟɧɬ ɮɚɡɵ ɢ ɮɚɡɨɜɚɹ ɫɤɨɪɨɫɬɶ
ɪɚɫɩɪɨɫɬɪɚɧɟɧɢɹ ɷɥɟɤɬɪɨɦɚɝɧɢɬɧɨɣ ɜɨɥɧɵ
