Nakahara M. Geometry, Topology and Physics

Подождите немного. Документ загружается.

Then the expectation value of

A(t) with respect to an arbitrary state

|ψ=



|n ψ

=n|ψ

ψ|

A(t)|ψ=



m,n

∗

m|

A(t)|n=



|ψ

From the fact that the result of the measurement of A in state |n is always a

,it

follows that the probability of the outcome of the measurement being a

,thatis

the probability of |ψ being in |n,is

|ψ

=|n|ψ|

The number n|ψ represents the ‘weight’ of the state |n in the state |ψ and is

called the probability amplitude.

A has a continuous spectrum a,thestate|ψ is expanded as

|ψ=



da ψ(a)|a.

The completeness relation now takes the form



da |aa|=I. (1.36)

Then, from the identity





a



|a=|a, one must have the normalization

a



|a=δ(a



− a), (1.37)

where δ(a) is the Dirac δ-function. The expansion coefﬁcient ψ(a) is obtained

from this normalization condition as ψ(a) =a|ψ.If|ψ is normalized as

ψ|ψ=1, one should have

1 =



da da



∗

(a)ψ(a



)a|a



=



da |ψ(a)|

It also follows from the relation

ψ|

A|ψ=



a|ψ(a)|

that the probability with which the measured value of A is found in the interval

[a, a + da] is |ψ(a)|

da. Therefore, the probability density is given by

ρ(a) =|a|ψ|

. (1.38)

Finally let us clarify why axiom A5 is required. Suppose that the system

is in the state |ψ and assume that the probability of the state to be in |φ

simultaneously is |ψ|φ|

. This has already been mentioned, when |ψ is an

eigenstate of some observable. Axiom A5 asserts that this is true for an arbitrary

state |ψ.

1.2.3 Heisenberg equation, Heisenberg picture and Schr

odinger picture

The formal solution to the Heisenberg equation of motion

[

H ]

is easily obtained as

A(t) = e

A(0)e

−i

. (1.39)

Therefore, the operators

A(t) and

A(0) are related by the unitary operator

U(t) = e

−i

(1.40)

and, hence, are unitary equivalent. This formalism, in which operators depend on

t, while states do not, is called the Heisenberg picture.

It is possible to introduce another picture which is equivalent to the

Heisenberg picture. Let us write down the expectation value of

A with respect

to the state |ψ as



A(t)=ψ|e

A(0)e

−i

|ψ

= (ψ|e

)

A(0)(e

−i

|ψ).

If we write |ψ(t)≡e

−i

|ψ, we ﬁnd that the expectation value at t is also

expressed as



A(t)=ψ(t)|

A(0)|ψ(t). (1.41)

Thus, states depend on t while operators do not in this formalism. This formalism

is called the Schr

odinger picture.

Our next task is to ﬁnd the equation of motion for |ψ(t). To avoid confusion,

quantities associated with the Schr¨odinger picture (the Heisenberg picture) are

denoted with the subscript S (H), respectively. Thus, |ψ(t)

= e

−i

|ψ

and

(0). By differentiating |ψ(t)

with respect to t, one ﬁnds the

Schr

odinger equation:

|ψ(t)

H|ψ(t)

. (1.42)

Note that the Hamiltonian

H is the same for both the Schr¨odinger picture and the

Heisenberg picture. We will drop the subscripts S and H whenever this does not

cause confusion.

1.2.4 Wavefunction

Let us consider a particle moving on the real line

and let ˆx be the position

operator with the eigenvalue y and the corresponding eigenvector |y; ˆx |y=

y|y. The eigenvectors are normalized as x|y=δ(x − y).

Similarly, let q be the eigenvalue of ˆp with the eigenvector |q; ˆp|q=q|q

such that p|q=δ(p − q).

Let |ψ∈

be a state. The inner product

ψ(x) ≡x |ψ (1.43)

is the component of |ψ in the basis |x,

|ψ=



|xx| dx |ψ=



ψ(x)|x dx.

The coefﬁcient ψ(x) ∈

is called the wavefunction. According to the

earlier axioms of quantum mechanics outlined, it is the probability amplitude of

ﬁnding the particle at x in the state |ψ, namely |ψ(x )|

dx is the probability of

ﬁnding the particle in the interval [x , x + dx]. Then it is natural to impose the

normalization condition



dx |ψ(x)|

=ψ|ψ=1 (1.44)

since the probability of ﬁnding the particle anywhere on the real line is always

unity.

Similarly, ψ(p) =p|ψ is the probability amplitude of ﬁnding the particle

in the state with the momentum p and the probability of ﬁnding the momentum

of the particle in the interval [p, p + dp] is |ψ(p)|

d p.

The inner product of two states in terms of the wavefunctions is

ψ|φ=



dx ψ|x x |φ=



dx ψ

∗

(x )φ(x), (1.45a)



d p ψ|pp|φ=



d p ψ

∗

( p)φ( p). (1.45b)

An abstract ket vector is now expressed in terms of a more concrete

wavefunction ψ(x ) or ψ(p). What about the operators? Now we write down the

operators in the basis |x . From the deﬁning equation ˆx|x =x|x, one obtains

x |ˆx =x |x , which yields after multiplication by |ψ from the right,

x |ˆx|ψ=xx|ψ=x ψ(x ). (1.46)

This is often written as ( ˆxψ)(x) = x ψ(x ).

What about the momentum operator ˆp? Let us consider the unitary operator

U(a) = e

−ia ˆp

Lemma 1.1. The operator

U(a) deﬁned as before satisﬁes

U(a)|x=|x + a. (1.47)

Proof. It follows from [ˆx, ˆp]=ithat[ˆx , ˆp

]=in ˆp

n−1

for n = 1, 2,....

Accordingly, we have

[ˆx,

U (a)]=



ˆx,



(−ia)

ˆp



= a

U(a)

which can also be written as

ˆx

U(a)|x=

U(a)( ˆx + a)|x =(x + a)

U(a)|x .

This shows that

U(a)|x∝|x + a.Since

U (a) is unitary, it preseves the norm

of a vector. Thus,

U(a)|x=|x + a.

Let us take an inﬁnitesimal number ε.Then

U(ε)|x =|x + ε(1 − iε ˆp)|x.

It follows from this that

ˆp|x =

|x + ε−|x

−iε

ε→0

−→ i

|x (1.48)

and its dual

x |ˆp =

x + ε|−x|

iε

ε→0

−→ −i

x |. (1.49)

Therefore, for any state |ψ, one obtains

x |ˆp|ψ=−i

x |ψ=−i

ψ(x). (1.50)

This is also written as ( ˆpψ)(x) =−idψ(x )/dx.

Similarly, if one uses a basis |p, one will have the momentum representation

of the operators as

ˆx|p= −i

d p

|p (1.51)

ˆp|p=p|p (1.52)

p|ˆx|ψ=i

d p

ψ(p) (1.53)

p|ˆp|ψ=pψ(p). (1.54)

Exercise 1.2. Prove (1.51)–(1.54).

Proposition 1.1.

x |p=

√

2π

i px

(1.55)

p|x =

√

2π

−i px

(1.56)

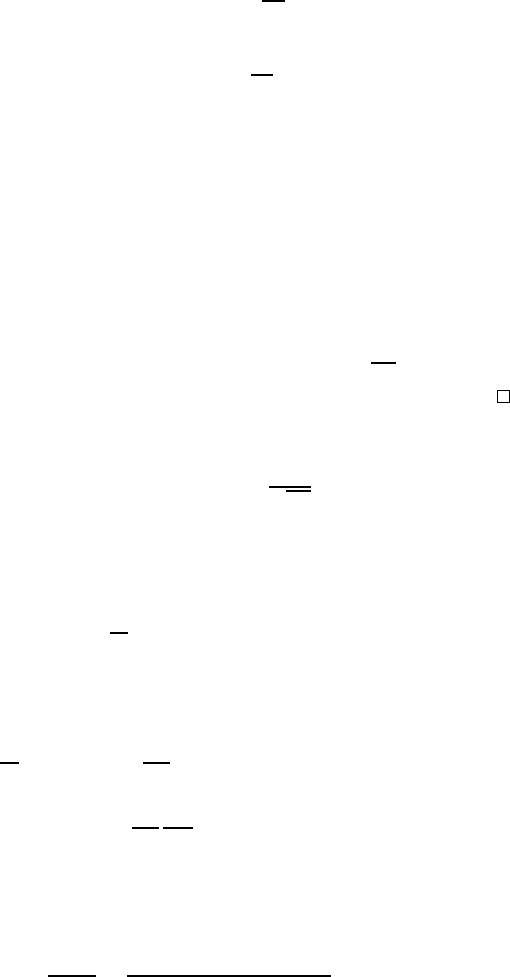
Proof.Take|ψ=|p in the relation

( ˆpψ)(x) =x |ˆp|ψ=−i

ψ(x)

to ﬁnd

px |p=x|ˆp|p=−i

x |p.

The solution is easily found to be

x |p=Ce

i px

The normalization condition requires that

δ(x − y) =x|y=x|



|pp| d p |y

= C



d p e

i p(x−y)

= C

2πδ(x − y),

where C has been taken to be real. This shows that C = 1/

√

2π. The proof of

(1.56) is left as an exercise.

Thus, ψ(x ) and ψ(p) are related as

ψ(p) =p|ψ=



dx p|xx |ψ=



√

2π

−i px

ψ(x) (1.57)

which is nothing other than the Fourier transform of ψ(x ).

Let us next derive the Schr¨odinger equation which ψ(x) satisﬁes. By

applying x | on (1.42) from the left, we obtain

x |i

|ψ(t)=x|

H|ψ(t)

where the subscript S has been dropped. For a Hamiltonian of the type

H =

ˆp

/2m + V ( ˆx ), we obtain the time-dependent Schr

odinger equation:

ψ(x, t) =





ˆp

+ V ( ˆx)



ψ(t)



=−

ψ(x, t) + V (x)ψ(x, t), (1.58)

where ψ(x, t) ≡x|ψ(t).

Suppose a solution of this equation is written in the form ψ(x, t) =

T (t)φ(x ). By substituting this into (1.58) and dividing the result by ψ(x , t),

we obtain



(t)

T (t)

−φ



(x )/2m + V (x)φ(x )

φ(x)

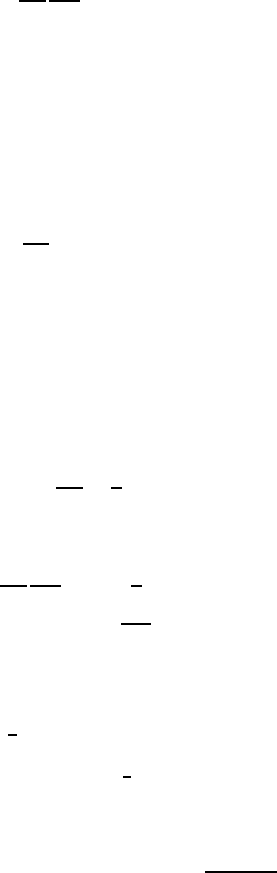
where the prime denotes the derivative with respect to a relevant variable. Since

the LHS is a function of t only while the right-hand side (RHS) of x only, they

must be a constant, which we label E. Accordingly, there are two equations,

which should be solved simultaneously,



(t) = ET(t) (1.59)

−

φ(x) + V (x )φ(x) = Eφ(x). (1.60)

The ﬁrst equation is easily solved to yield

T (t) = exp(−iEt) (1.61)

while the second one is the eigenvalue problem of the Hamiltonian operator

and called the time-independent Schr

odinger equation,thestationary state

Schr

odinger equation or, simply, the Schr

odinger equation. For three-

dimensional space, it is written as

−

∇

φ(x) + V (x)φ(x) = Eφ(x). (1.62)

1.2.5 Harmonic oscillator

It is instructive to stop here for the moment and work out some non-trivial

example. We take a one-dimensional harmonic oscillator as an example since

it is not trivial, it is still solvable exactly and it is very important in the folllowing

applications.

The Hamiltonian operator is

H =

ˆp

mω

ˆx

[ˆx, ˆp]=i. (1.63)

The (time-independent) Schr¨odinger equation is

−

ψ(x) +

mω

ψ(x) = Eψ(x). (1.64)

By rescaling the variables as ξ =

√

mωx , ε = E/

hω, one arrives at



+ (ε − ξ

)ψ = 0. (1.65)

The normalizable solution of this ordinary differential equation (ODE) exists only

when ε = ε

≡ (n +

)(n = 0, 1, 2,...)namely

E = E

≡ (n +

)ω (n = 0, 1, 2,...) (1.66)

and the normalized solution is written in terms of the Hermite polynomial

(ξ) = (−1)

−ξ

dξ

(1.67)

ψ(ξ) =



mω

√

(ξ)e

−ξ

. (1.68)

This eigenvalue problem can also be analysed by an algebraic method.

Deﬁne the annihilation operator ˆa and the creation operator ˆa

†

ˆa =



mω

ˆx + i



2mω

ˆp (1.69)

ˆa

†



mω

ˆx − i



2mω

ˆp. (1.70)

The number operator

N is deﬁned by

N =ˆa

†

ˆa. (1.71)

Exercise 1.3. Show that

[ˆa, ˆa]=[ˆa

†

, ˆa

†

]=0 [ˆa, ˆa

†

]=1 (1.72)

and

[

N, ˆa]=−ˆa [

N , ˆa

†

]=ˆa

†

. (1.73)

Show also that

H = (

N +

)ω. (1.74)

Let |n be a normalized eigenvector of

N ,

N|n=n|n.

Then it follows from the commutation relations proved in exercise 1.3 that

N( ˆa|n) = ( ˆa

N −ˆa)|n=(n − 1)( ˆa|n)

N ( ˆa

†

|n) = ( ˆa

†

N +ˆa

†

)|n=(n + 1)( ˆa

†

|n).

Therefore, ˆa decreases the eigenvalue by one while ˆa

†

increases it by one, hence

the name annihilation and creation. Note that the eigenvalue n ≥ 0since

n =n|

N |n=(n|ˆa

†

)( ˆa|n) =ˆa|n

≥ 0.

The equality holds if and only if ˆa|n=0. Take a ﬁxed n

> 0 and apply ˆa

many times on |n

. Eventually the eigenvalue of ˆa

 will be negative for

some integer k > n

, which is a contradiction. This can be avoided only when n

is a non-negative integer. Thus, there exists a state |0 which satisﬁes ˆa|0=0.

The state |0 is called the ground state.Since

N|0=ˆa

†

ˆa|0=0, this state is

the eigenvector of

N with the eigenvalue 0. The wavefunction ψ

(x ) ≡x |0 is

obtained by solving the ﬁrst-order ODE

x |ˆa|0=



2mω



(x ) + mωxψ

(x )



= 0. (1.75)

The solution is easily found to be

(x ) = C exp(−mωx

/2) (1.76)

where C is the normalization constant given in (1.68). An arbitrary vector |n is

obtained from |0 by a repeated application of ˆa

†

Exercise 1.4. Show that

|n=

√

( ˆa

†

)

|0 (1.77)

satisﬁes

N|n=n|n and is normalized.

Thus, the spectrum of

N turns out to be Spec

N ={0, 1, 2,...} and hence

the spectrum of the Hamiltonian is

Spec

H ={

,...}. (1.78)

1.3 Path integral quantization of a Bose particle

The canonical quantization of a classical system has been discussed in the

previous section. There the main role was played by the Hamiltonian and the

Lagrangian did not show up at all. In the present section, it will be shown that

there exists a quantization process, called the path integral quantization, based

heavily on the Lagrangian.

1.3.1 Path integral quantization

We start our analysis with one-dimensional systems. Let ˆx(t) be the position

operator in the Heisenberg picture. Suppose the particle is found at x

at time

(>0). Then the probability amplitude of ﬁnding this particle at x

at later time

(>t

) is

x

, t

 (1.79)

where the vectors are deﬁned in the Heisenberg picture,

ˆx(t

)|x

, t

=x

, t

 (1.80)

ˆx(t

)|x

, t

=x

, t

. (1.81)

We have dropped S and H again to simplify the notation. Note that |x

, t

 is an instantaneous

eigenvector and hence parametrized by the time t

when the position is measured. This should not be

confused with the dynamical time dependence of a wavefunction in the Schr ¨odinger picture.

The probability amplitude (1.79) is also called the transition amplitude.

Let us rewrite the probability amplitude in terms of the Schr¨odinger picture.

Let ˆx =ˆx(0) be the position operator with the eigenvector

ˆx|x=x|x . (1.82)

Since ˆx has no time dependence, its eigenvector should be also time independent.

ˆx(t

) = e

ˆxe

−i

(1.83)

is substituted into (1.80), we obtain

ˆxe

−i

, t

=x

, t

.

By multiplying e

−i

from the left, we ﬁnd

ˆx[e

−i

, t

] = x

−i

, t

].

This shows that the two eigenvectors are related as

, t

=e

. (1.84)

Similarly, we have

, t

=e

, (1.85)

from which we obtain

x

, t

|=x

−i

. (1.86)

From these results, we express the probability amplitude in the Schr¨odinger

picture as

x

, t

=x

−i

H(t

−t

)

. (1.87)

In general, the function

h(x , y;β) ≡x|e

−

Hβ

|y (1.88)

is called the heat kernel of

H . This nomenclature originates from the similarity

between the Schr¨odinger equation and the heat equation. The amplitude (1.87) is

the heat kernel of

H with imaginary β:

x

, t

=h(x

, x

;i(t

− t

)). (1.89)

Now the amplitude (1.87) is expressed in the path integral formalism. To

this end, we consider the case in which t

− t

= ε is an inﬁnitesimal positive

number. Let us put x

= x and x

= y to simplify the notation and suppose the

Hamiltonian is of the form

H =

ˆp

+ V ( ˆx). (1.90)

y = -x

- R

-plane

Figure 1.1. The integration contour.

We ﬁrst prove the following lemma.

Lemma 1.2. Let a be a positive constant. Then



∞

−∞

−iap

d p =



. (1.91)

Proof. The integral is different from an ordinary Gaussian integral in that the

coefﬁcient of p

is a pure imaginary number. First replace p by z = x + iy.The

integrand exp(−iaz

) is analytic in the whole z-plane. Now change the integration

contour from the real axis to the one shown in ﬁgure 1.1. Along path 1, we have

dz = dx and hence this path gives the same contribution as the original integration

(1.91). The contribution from paths 2 and 4 vanishes as R →∞. Noting that the

variable along path 3 is z = (1 − i)x , we evaluate the contribution from this path

(1 −i)



−∞

∞

−2ax

dx =−e

−iπ/4



The summation of all the contribution must vanish due to Cauchy’s theorem and,

hence,



∞

−∞

d p e

−iap

= e

−iπ/4



Now this lemma is employed to obtain the heat kernel for an inﬁnitesimal

time interval.

Proposition 1.2. Let

H be a Hamiltonian of the form (1.90) and ε be an

inﬁnitesimal positive number. Then for any x, y ∈

,weﬁndthat

x |e

−i

Hε

|y=

√

2πiε

exp



iε





(x − y)



− V



x + y



(ε

) + (ε(x − y)

)



. (1.92)