Nair S. Advanced Topics in Applied Mathematics: For Engineering and the Physical Sciences

Подождите немного. Документ загружается.

Laplace Transforms 189

In this case, terms of the form

(1)

p −p

(2)

p −p

, (4.82)

can be combined to obtain

(1)

(p −λ

) +b

(2)

(p −λ

)

+ω

, (4.83)

which can be inverted in terms e

cosω

t and e

sinω

Example: Vibrations

For a spring and mass system with mass m and spring constant k, the

equation of motion may be written as

m¨u +ku =f (t), u(0) =˙u(0) =0, (4.84)

where f is the force exciting the system. Using

=k/m, (4.85)

the Laplace transform gives

¯u =¯g

f , (4.86)

where

¯g =

+ω

. (4.87)

Inverting,

g(t) =

mω

sinωt, (4.88)

and the solution is

u(t) =

mω



sinω(t −τ)f (τ )dτ . (4.89)

190 Advanced Topics in Applied Mathematics

Example: Higher-Order Differential Equation

Consider the differential equation

−6

+14

−16

+8u =t, (4.90)

with the initial conditions

(0) =

(0) =u(0) =0. (4.91)

Taking the Laplace transform

¯u =

−6p

+14p

−16p +8)

. (4.92)

By inspection, we ﬁnd p = 2 is a double zero. Removing the factors

(p −2)

and p

, what remains is p

−2p +2, which can be written as

[(p −1)

+1]. Thus,

¯u =

(p −2)

[(p −1)

+1]

. (4.93)

A partial fraction expansion of the right-hand side expression is

(p −2)

[(p −1)

+1]

(p −2)

p +C

[(p −1)

+1]

, (4.94)

where the constants A

,..., C

have to be found. Multiplying both sides

by p

and setting p =0, we ﬁnd

, (4.95)

and multiplying with (p −2)

and setting p =2,

. (4.96)

The quadratic expression [(p −1)

+1] can be factored as (p −1 −i)

(p −1 +i). Multiplying by the quadratic and setting p =1 ±i gives

=0, C

. (4.97)

Laplace Transforms 191

The remaining constants are found as

, B

=−

, (4.98)

by setting p to two arbitrary numbers other than the zeros of the

denominator of ¯u, say, p =1andp =−1. Finally,

¯u =



−

p −2

(p −2)

(p −1)



, (4.99)

which has the inverse

u =

[2 +t −2e

+te

+2e

sint]. (4.100)

4.9.2 Boundary Value Problems

In some problems, the differential equation is supplemented with

boundary conditions, instead of the initial conditions we have assumed

so far. In such cases, we substitute unknown constants for the missing

initial conditions while taking the Laplace transform, and solve for

these constants using the unused boundary conditions after inverting

the solution. Most of the time, differential equations containing an

unknown space-dependent variable come with boundary conditions.

4.9.3 Partial Differential Equations

We consider two examples of partial differential equations: transient

heat conduction in a semi-inﬁnite bar and wave propagation in a semi-

inﬁnite string.

Example: Transient Heat Conduction

With u representing the relative temperature above the ambient, the

heat conduction in a semi-inﬁnite bar is described by the equation

∂

∂x

∂u

∂t

,0< x < ∞,0< t < ∞, (4.101)

192 Advanced Topics in Applied Mathematics

where κ is the diffusivity. We assume

u(x,0) =0, u(0,t) =f (t), u(x,t) →0, as x →∞. (4.102)

Taking the transform

L[u(x,t),t → p]=¯u(x, p), (4.103)

∂

¯u

∂x

=p¯u. (4.104)

This second-order ordinary differential equation in x has the general

solution

¯u = Ae

−

√

p/κx

+Be

√

p/κx

. (4.105)

As u →0asx →∞, B =0.

The end condition u(0,t) =f (t) transforms into ¯u(0,p) =

f , and we

ﬁnd

A =

f . (4.106)

Then

¯u(x,p) =

−

√

p/κx

. (4.107)

Using convolution, the solution has the form

u(x,t) =



g(t −τ)f (τ )dτ , (4.108)

where the Green’s function g is given by

g(t) =L

−1

−

√

p/κx

]

√

4πκt

−x

/(4κt)

, (4.109)

wherewehaveusedEq.(4.60).Inthecaseofasuddenincreasein

temperature, T

, at the end of the bar x =0, we have

f (t) =T

, (4.110)

¯u(x,p) =

−

√

p/κx

, (4.111)

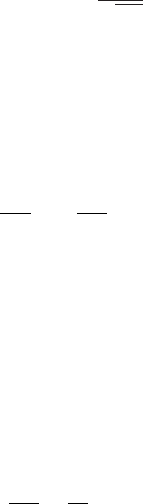
Laplace Transforms 193

and we may invert this directly using Eq. (4.62), without resorting to

convolution, in the form

u(x,t) =T

erfc



√

4κt



. (4.112)

Example: Wave Propagation in a Semi-inﬁnite String

We consider a taut string occupying 0 < x < ∞. The differential

equation describing the perpendicular displacement is

∂

∂t

∂

∂x

, (4.113)

where c is the wave speed that depends on the tension in the string and

the density of the string material. We assume the boundary and initial

conditions:

u(x,0) =˙u(x,0) =0, u(0, t) =f (t), u(x,t) →0asx →∞.

(4.114)

Taking the transform, we obtain the second-order differential equation

in x,

∂

¯u

∂x

¯u, (4.115)

which has the solution

¯u = Ae

−px/c

+Be

px/c

. (4.116)

As it is required for the solution to vanish at inﬁnity, B =0. Using the

end condition, ¯u(0,p) =

f ,weﬁnd

A =

f , (4.117)

¯u =

−px/c

. (4.118)

Noting that the effect of the exponential factor is a shift in time,

u(x,t) =f (t −x/c)h(t −x/c), (4.119)

194 Advanced Topics in Applied Mathematics

where we have used the Heaviside step function for clarity. It can be

seen that the disturbance imparted to the end, x =0, travels along the

string with a speed of c.

Example: D’Alembert Solution for Waves in an Inﬁnite String

In an inﬁnite string, if the displacement and velocities are prescribed

initially, we have

∂

∂t

∂

∂x

, (4.120)

u(x,0) =f (x), ˙u(x,0) =g(x). (4.121)

Taking the transform

¯u −pf (x) −g(x) =c

∂

¯u

∂x

, (4.122)

where, as before,

¯u = L[u(x, t), t → p]. (4.123)

Next, we take the Fourier transform of ¯u(x, p),

U(ξ, p) = F [¯u(x,p), x → ξ ]. (4.124)

Now the differential equation is

)

U = pF(ξ ) +G(ξ ),

U =

pF(ξ ) +G(ξ )

. (4.125)

Inverting the Laplace transform ﬁrst and then the Fourier transform,

U =



ictξ

−ictξ



F(ξ ) +

2icξ



ictξ

−e

−ictξ



G(ξ )



ictξ

−ictξ



F(ξ ) +



−t

icτξ

G(ξ )dτ,

Laplace Transforms 195

u(x,t) =



f (x +ct) +f (x −ct) +



−t

g(x −cτ)dτ





f (x +ct) +f (x −ct) +



x+ct

x−ct

g(x



)dx





, (4.126)

where we have used x



=x −cτ .

The traditional derivation of this result uses new variables (not to

be confused with the Fourier variable),

ξ =x +ct, η = x −ct, (4.127)

to have

∂

∂x

∂

∂ξ

∂

∂η

∂

∂t

∂

∂ξ

−

∂

∂η

. (4.128)

In these new variables, the wave equation becomes

∂

∂ξ∂η

=0. (4.129)

This equation, after integration, gives the solution in terms of two

arbitrary functions, F and G, in the form,

u =F(ξ ) +G(η) =F(x +ct) +G(x −ct). (4.130)

From the initial conditions,

F(x) +G(x) =f (x), F



(x) −G



(x) =g(x)/c. (4.131)

Integrating the second relation,

F(x) −G(x) =



g(x



)dx



, (4.132)

and solving for F and G,

F(x) =



f (x) +



g(x



)dx





, (4.133)

G(x) =



f (x) −



g(x



)dx





. (4.134)

196 Advanced Topics in Applied Mathematics

With these

u =



f (x +ct) +f (x −ct) +



x+ct

x−ct

g(x



)dx





. (4.135)

The new variables, ξ =x+ct and η =x−ct, are called the characteristic

variables. In the (x,t)-plane, a ﬁxed value of ξ or η corresponds to a

straight line known as the characteristic line. The initial conditions

propagate along the characteristic lines.

4.9.4 Integral Equations

Integral equations containing convolution integrals may be solved

using the Laplace transform. Of course, the convolution integrals must

be suitable for the Laplace transform.

Example: Volterra Equation

Consider the integral equation

u(t) +λ



g(t −τ)u(τ )dτ =f (t), (4.136)

where λ is a constant. Kernels of the form g(t −τ)are called hereditary

kernels as they express the history of the unknown, u. Taking the

transform

(1 +λ¯g) ¯u =

f , (4.137)

¯u =

1 +λ¯g

. (4.138)

If we can invert this expression, we obtain the solution. In the special

case,

g(t) =e

−t

, ¯g =

p +1

, (4.139)

¯u =

(p +1)

p +λ +1

f −λ

p +λ +1

, (4.140)

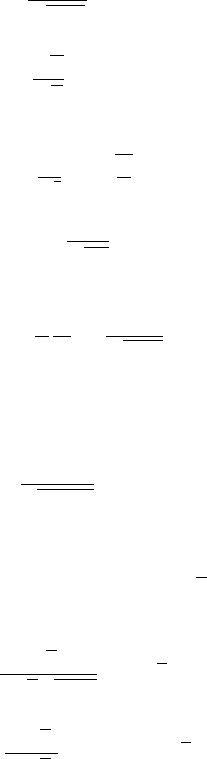
Laplace Transforms 197

which can be inverted to obtain

u(t) =f (t) −λ



−(λ+1)(t−τ)

f (τ )dτ. (4.141)

Example: Abel Equation

The Abel equation,



u(τ )dτ

√

t −τ

=f (t), (4.142)

transforms to

√

¯u =

f , (4.143)

where we have used



√





, (4.144)

¯u =

√

πp

. (4.145)

Inversion yields

u(t) =



f (τ )dτ

√

t −τ

. (4.146)

Example: Generalized Abel Equation

A slight modiﬁcation of the Abel equation has the form



u(τ )dτ

√

−τ

=f (t). (4.147)

We may introduce new variables

x =t

, ξ =τ

, dτ =dξ/(2



ξ), (4.148)

to obtain



√

ξ)dξ

√

x −ξ

=f (

√

x). (4.149)

Let

v(ξ ) =

√

ξ)

√

, g(x) =f (

√

x). (4.150)

198 Advanced Topics in Applied Mathematics

Now we have the Abel equation,



v(ξ )dξ

√

x −ξ

=g(x), (4.151)

which has the solution

v(x) =



g(ξ )dξ

√

x −ξ

. (4.152)

In terms of the original variables,

u(t) =



f (τ )τdτ

√

−τ

. (4.153)

4.9.5 Cagniard–De Hoop Method

To solve partial differential equations involving inﬁnite spaces and

time, we may use the Laplace and Fourier transforms simultaneously

as we have done with the multiple Fourier transforms. Once the trans-

form of the unknown function is isolated, it can be inverted using the

inverse integrals sequentially. The Cagniard-De Hoop method uses the

Fourier inverse ﬁrst, and the line integral from −∞to ∞is distorted to

look like a Laplace transform. In this way the inverse of the two trans-

forms are obtained without any contour integration if there are no

singularities between the original contour and the distorted contour.

We illustrate this method using a semi-inﬁnite medium, −∞ < x <

∞,0 < y < ∞ at a quiescent pressure, p

. At time, t = 0, an addi-

tional pressure of magnitude P

f (x) is applied on the surface y = 0. It

is assumed that the pressure ﬂuctuations p(x, y,t) above the ambient

pressure p

satisfy

∇

p =

∂

∂t

, (4.154)

where c is the speed of sound. The boundary conditions are

p(x,0,t) =P

f (x)h(t), p →0asr →∞, (4.155)

where r =

