Мордасов М.М., Трофимов А.В. Анализ и синтез пневматических устройств. Учебное пособие
Подождите немного. Документ загружается.




Приложение 5
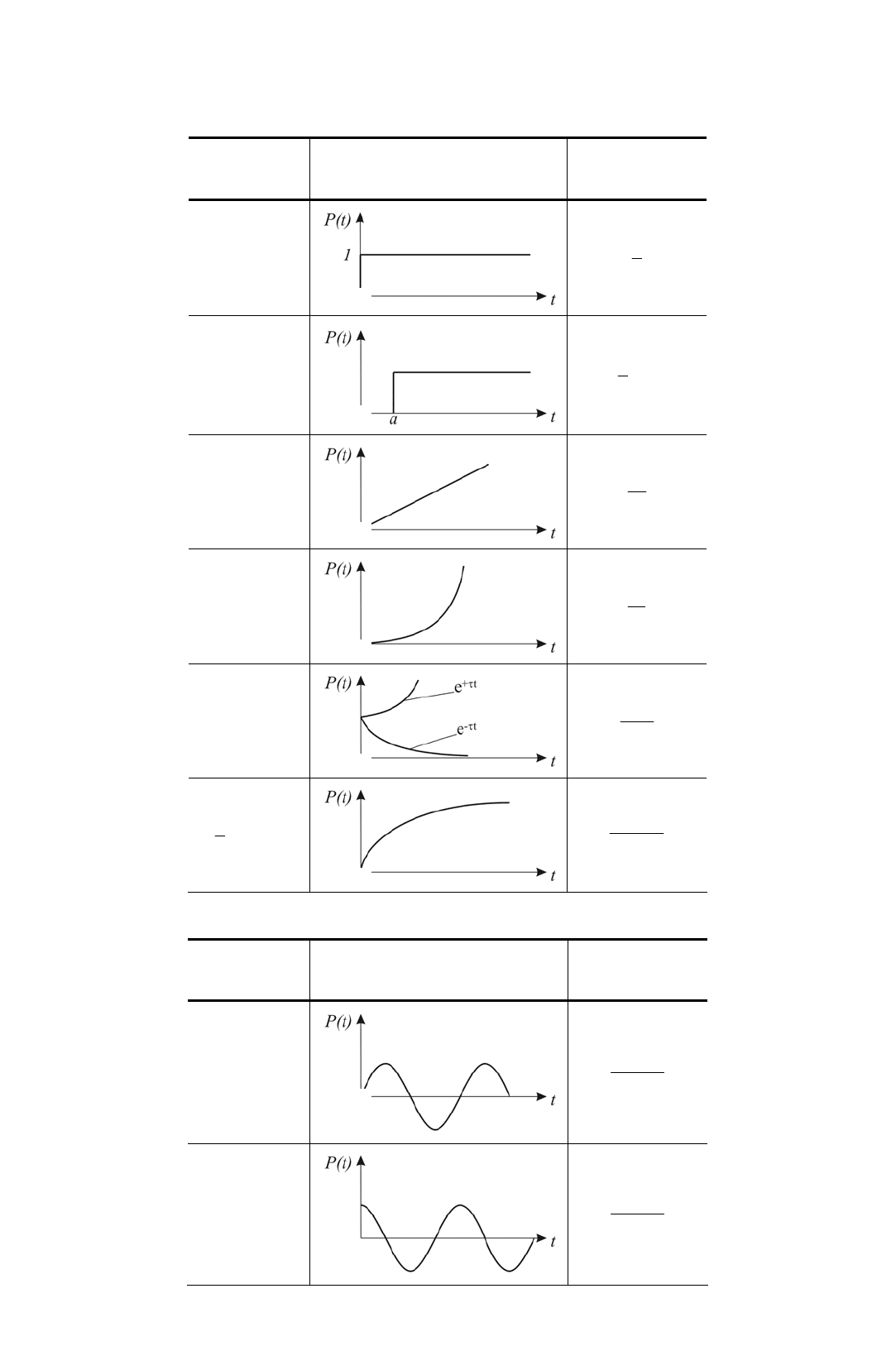
Преобразование Лапласа для некоторых функций,
встречающихся при анализе и синтезе
Оригинал
P(t)
График функции P(t) Изображение
P(s)
(
)
t1
s
1
()
at
−
1
as
e
s
−
1
t
2
1
s
2
t
3
1
s
t
e
τ±
τm
s
1
()
t
e
τ−
−
τ
1
1
)(
1
τ+ss
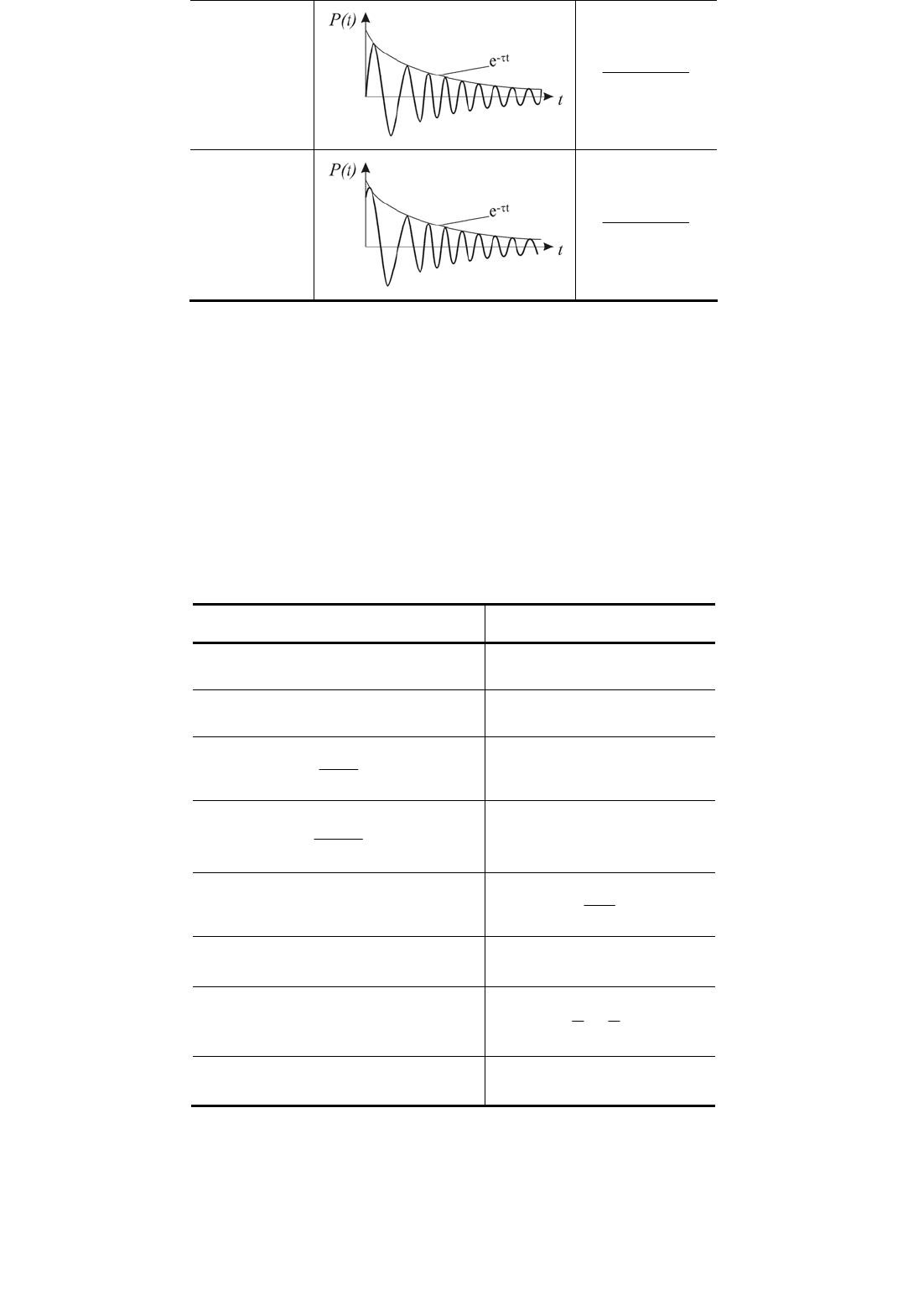
Продолжение прил. 5
Оригинал
P(t)
График функции P(t)
Изображение
P(s)
t
ω
sin
22
ω+
ω
s
t
ω
cos
22
ω+s
s
P (t)
P (t)
P (t)
P (t)
P (t)
P (t)
t
t
t
t
t
t
a
1
e
+τ
t
e
–τ
t
P (t)
P (t)
P (t)
t
e
–τt
te
t
ω
τ−
sin
()
2
2
ω+τ+
τ
s
te
t
ω
τ−
cos
()
2
2
ω+τ+
τ
+
s
s
Приложение 6
Преобразование Лапласа для типовых математических операций
P(t) – оригинал P(s) – изображение
()
taP
(
)
saP
() ()
tPtP
21
±
(
)
(
)
sPsP
21
±
()
d
t
tdP
(
)
(
)
0PssP
−
()
2
2
dt
tPd
(
)
(
)
(
)
00
2
PsPsPs
′
−−
()
∫
dttP
(
)
s
sP
()
τ−tP
(
)
sPe
sτ−
()
atP , 0>a
a
s
P
a
1
()
tPe
at
(
)
asP
−
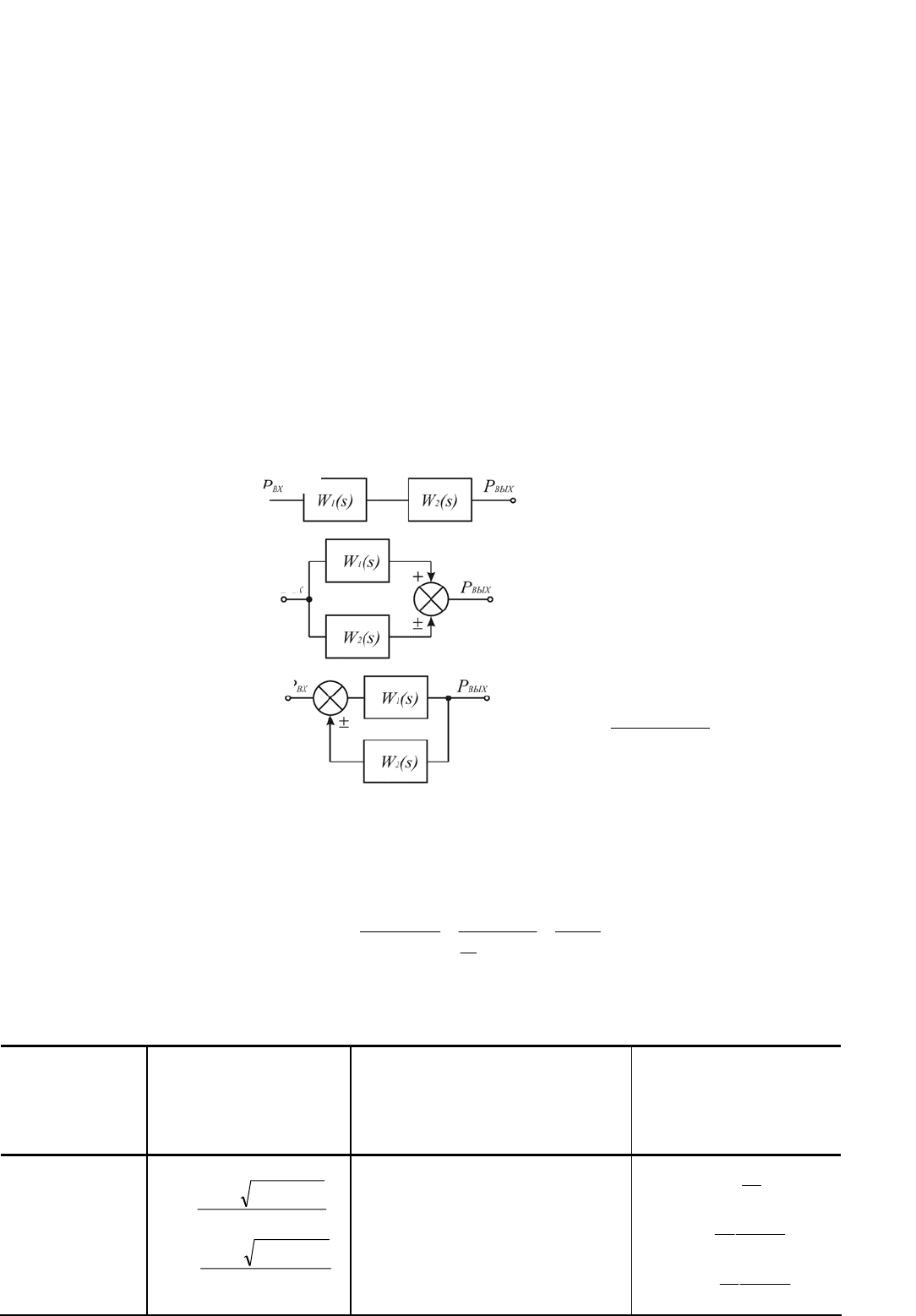
Приложение 7
Виды соединения звеньев
Динамической структурной схемой или просто структурной схемой системы автоматического регу-
лирования называют схему, составленную из типовых динамических звеньев.
Динамическим звеном называют часть системы, описываемую некоторым уравнением. Сложное
звено можно представить как несколько элементарных типовых звеньев, соединенных определенным
образом.
Обычно различают следующие типовые звенья: усилительное, инерционное, колебательное, интег-
рирующее, дифференцирующее, интегро-дифференцирующее, запаздывающее. Любое сложное звено
можно представить как соединение указанных выше типовых звеньев.
Включение звеньев системы может быть выполнено в виде трех основных форм: последовательное
(а), параллельное (б) или с обратной связью (в).
а
)
(
)
(
)()
sWsWsW
21
=
б
)
(
)
(
)()
sWsWsW
21
±=
в)
()
(
)
() ()
sWsW
sW
sW
21
1
1m
=
Если в прямой цепи системы, имеющей отрицательную обратную связь, располагается усилитель-
ное звено с большим коэффициентом усиления
(
)
1>>K , то передаточная функция
()
sW системы опреде-
ляется передаточной функцией
()
sW
ос
обратной связи:
()
()
()
()
sW
sW
K
sKW
K
sW
ос
ос
ос
1
1
1
1
=
+
=
+
=
.
1.5.1. Решение линейного дифференциального уравнения второго порядка
Значение
дискриминанта
характеристиче-
ского уравнения
Значение корней
характеристического
уравнения
Общее решение
дифференциального уравнения
Значение коэффициен-
тов
04
02
2
1
>− ааа
2
02
2
11
1
2
4
а
аааа −+−
=λ
;
2
02
2
11
2
2
4
а
аааа −−−
=λ
(
)
tt
eCeCCtP
21
210вых
λλ
++=
0
0
a
b
С =
;
12
2
0
1
λ−λ
λ−
=
a
b
C
;
12
1
0
2
λ−λ
λ
=
a
b
C
Р
вх
Р
вых
Р
вых
Р
вх
Р
вх
Р
вых
W
1
(s)
W
1
(s) W
2
(s)
W
2
(s)
W
2
(s)
W
1
(s)

04
02
2
1
=− ааа
2
1
21
2a
a−
=λ=λ=λ
(
)
(
)
t
etCCCtP
λ
++=
210вых
0
0
a
b
С =
;
0
1
a
b
C
−
=
;
0
2
a
b
C
λ
=
04
02
2
1
<− ааа
ir
µ
−=λ
1
; ir
µ
+=
λ
2
,
2
1
2a
a
r
−
=
,
2
102
4 aaa −=µ
(
)
021вых
)sincos( CtCtCetP
rt
+µ+µ=
0
0
a
b
С =
;
0
1
a
b
C
−
=
;
0
2
a
rb
C
µ
=
1.6.1. Результаты анализа математической модели процесса измерения
Исходные ус-
ловия
α = const, T =
const
G
и
V
1
V
2
Математическая модель
Началь-
ные ус-
ловия
Решение

Var Var Var
α=
α++
+α=
α++
)(
)(
)(
)(
);()(
)(
)(
)(
1
2
2
2
2
и2
1
1
1
1
tRTPRT
dt
tdV
tP
dt
tdP
V
tRTGtRTPRT
dt
tdV
tP
dt
tdP
V
P
1
(0) =
P
10
,
P
2
(0) =
P
20
,
V
1
(0) =
V
10
,
V
2
(0) =
V
20
,
G
и
(0) =
G
0
.
В общем виде в квадрату-
рах
неразрешимо
Var Con
st
Var
=
+
α
+τ
α
+=+τ
)(1
)(
1
)(
)(
;
)(
)()(
)(
1
2
2
2
2
и
21
1
1
tP
dt
tdV
RT
tP
dt
tdP
tG
tPtP
dt
tdP
P
1
(0) =
P
10
,
P
2
(0) =
P
20
,
V
2
(0) =
V
20
,
G
и
(0) =
G
0
.
В общем виде в квадрату-
рах
неразрешимо
Var Con
st
Con
st
=+τ
α
+=+τ
)()(
)(
;
)(
)()(
)(
12
2
2
и
21
1
1
tPtP
dt
tdP
tG
tPtP
dt
tdP
P
1
(0) =
P
10
,
P
2
(0) =
P
20
,
G
и
(0) =
G
0
.
;)(
)(
1
exp
)(
)(
)(
)(
)(
0
и
21
3
ср
2
21
2
2и
10
2
21
2
2и
ср1
∫
ττ
τ+τα
+
+
τ
−
−
τ+τα
τ
−+
+
τ+τα
τ
+=
t
dG
t
P
tG
P
tG
PtP
∫
ττ
τ+τα
+
+
τ
−
−
τ+τα
ττ
−+
+
τ+τα
ττ
+=
t
dG
t
P
tG
P
tG
PtP
0
и
21
3
10
2
21
21и
ср
2
21
21и
ср1
)(
)(
1
exp
)(
)(
)(
)(
)(
Продолжение табл. 1.6.1
Исходные ус-
ловия
α = const, T =
const
G
и
V
1
V
2
Математическая модель
Началь-
ные ус-
ловия
Решение
Con
st
Con
st
Con
st
=+τ
α
+=+τ
)()(
)(
;
)(
)()(
)(
12
2
2
и
21
1
1
tPtP
dt
tdP
tG
tPtP
dt
tdP
P
1
(0) =
P
10
,
P
2
(0) =
P
20
.
;
)(
exp
)(
)(
)(
)(
)(
21
0
3
ср
2
21
2
2и
10
2
21
2
2и
ср1
τ+τα
+
+
τ
−
−
τ+τα
τ
−+
+
τ+τα
τ
+=
tG
t
P
tG
P
tG
PtP
)(
exp
)(
)(
)(
)(
)(
21
0
3
20
2
21
2
2и
ср
2
21
21и
ср1
τ+τα
+
+
τ
−
−
τ+τα
τ
−+
+
τ+τα
ττ
+=
tG
t
P
tG
P
tG
PtP
0 Con
st
Con
st
=+τ
=+τ
)()(
)(
);()(
)(
12
2
2
21
1
1
tPtP
dt
tdP
tPtP
dt
tdP
P
1
(0) =
P
10
,
P
2
(0) =
P
20
,
P
10
> P
20
.
()
;
,exp)(
21
21
3
3
ср10ср1
τ+τ
ττ
=τ
τ
−−+=
t
PPPtP
()
21
202101
ср
3
20срср2
,exp)(
τ+τ
τ+τ
=
τ
−−−=
PP
P
t
PPPtP
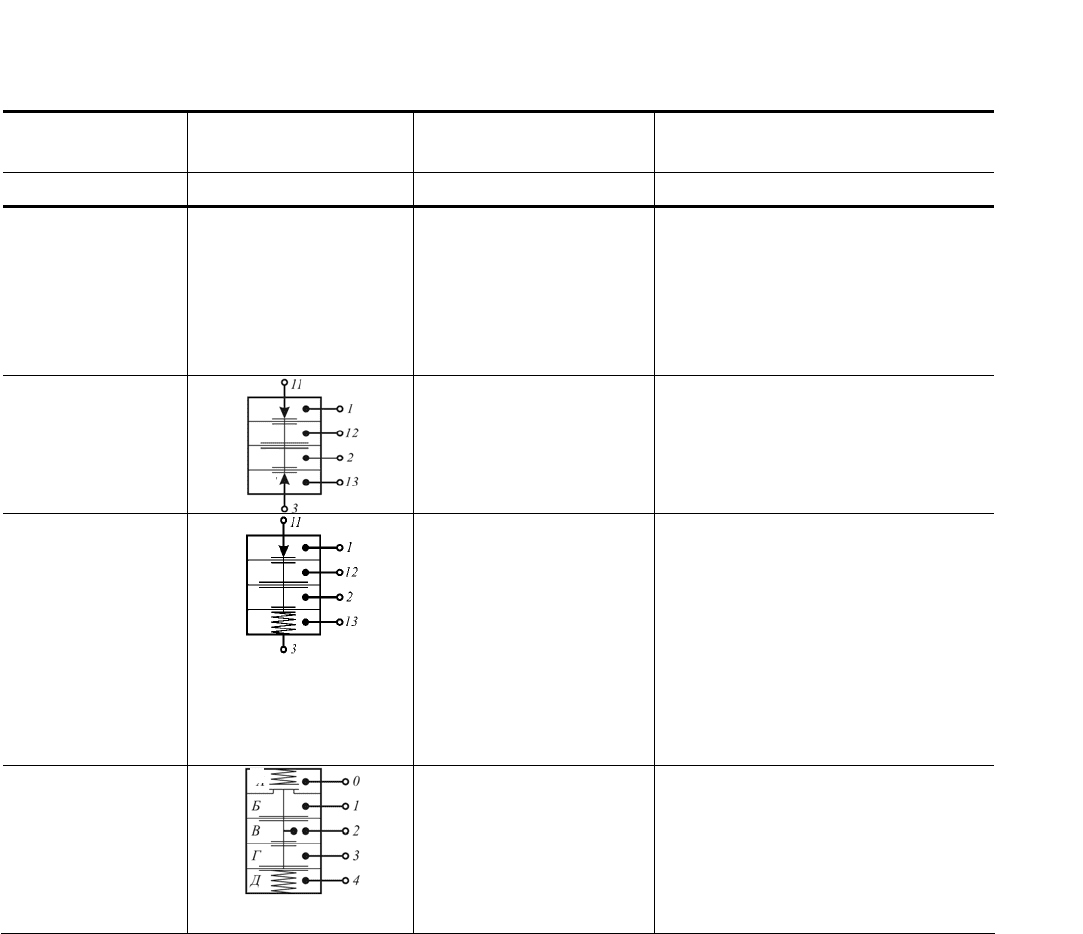
Приложение 4
Технические характеристики комплекса элементов УСЭППА
Название и тип
элемента
Конструкция эле-
мента
Назначение элемента Характеристики элемента
1 2 3 4
Индикатор
пневматический
типа ИП-1
Для визуального
представления дис-
кретной информации
посредством измене-
ния цвета показы-
вающего органа
Выходные пневматические
сигналы – дискретные "0" или
"1"
Реле трехмем-
бранное пневма-
тическое
типа П1Р.1
Для реализации логи-
ческих функций и
коммутации непре-
рывных сигналов
Выходные пневматические сиг-
налы – дискретные "0" или "1"
по ГОСТ 13053–67. Расход воз-
духа на выходе не менее 1,2 м
3
/ч
Реле трехмем-
бранное пневма-
тическое
типа П1Р.З
Для реализации логи-
ческих функций и
коммутации непре-
рывных сигналов. В
начальный момент
мембран блок нахо-
дится в определенном
положении под дей-
ствием пружины
Выходные пневматические сиг-
налы – дискретные "0" или "1"
по ГОСТ 13053–67. Расход воз-
духа на выходе не менее 1,2 м
3
/ч
Реле универ-
сальное пневма-
тическое
типа РУП-1М
Для реализации логи-
ческих функций и
коммутации непре-
рывных сигналов.
Мощный выходной
сигнал
Выходные пневматические сиг-
налы – дискретные "0" или "1"
по ГОСТ 13053–67. Расход воз-
духа на выходе не менее 5 м
3
/ч
А
Б
В
Г
А
Б
В
Г
А
Б
В
Г
Д

Продолжение прил. 4
1 2 3 4
