Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics

Подождите немного. Документ загружается.

R is a constant for the particular gas whose molecular weight is M.

Alternative units for R are kJ/kg

K, Btu/lb

8R, and ft

lbf/lb

8R.

Table 3.1 provides a sampling of values for the gas constant R calcu-

lated from Eq. 3.25.

Equation 3.21 can be expressed in terms of the compressibility fac-

tor as

lim

Z 5 1 (3.26)

That is, the compressibility factor Z tends to unity as pressure tends

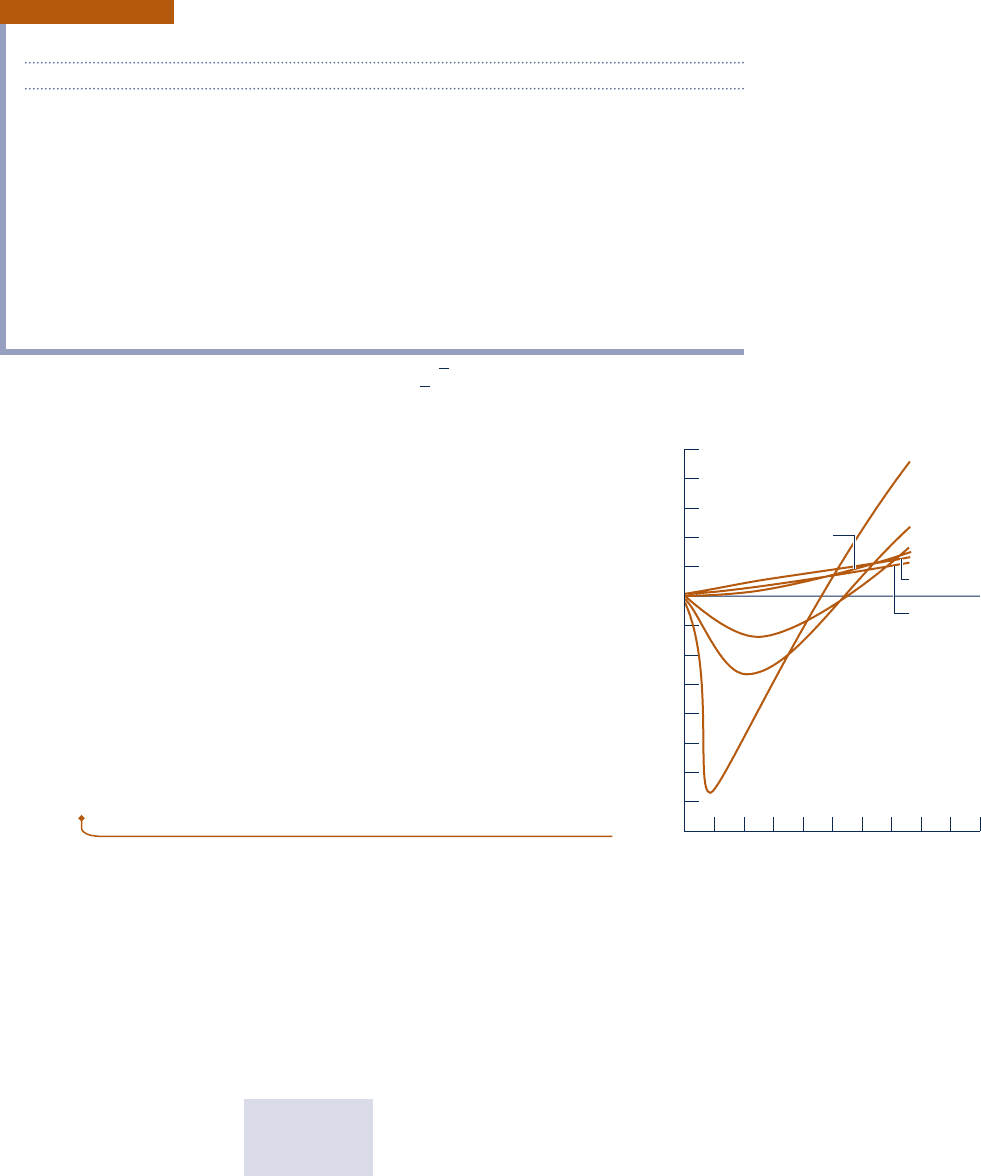
to zero at fixed temperature. This can be illustrated by reference to

Fig. 3.11, which shows Z for hydrogen plotted versus pressure at a

number of different temperatures. In general, at states of a gas where

pressure is small relative to the critical pressure, Z is approximately 1.

3.11.3

Generalized Compressibility Data, Z Chart

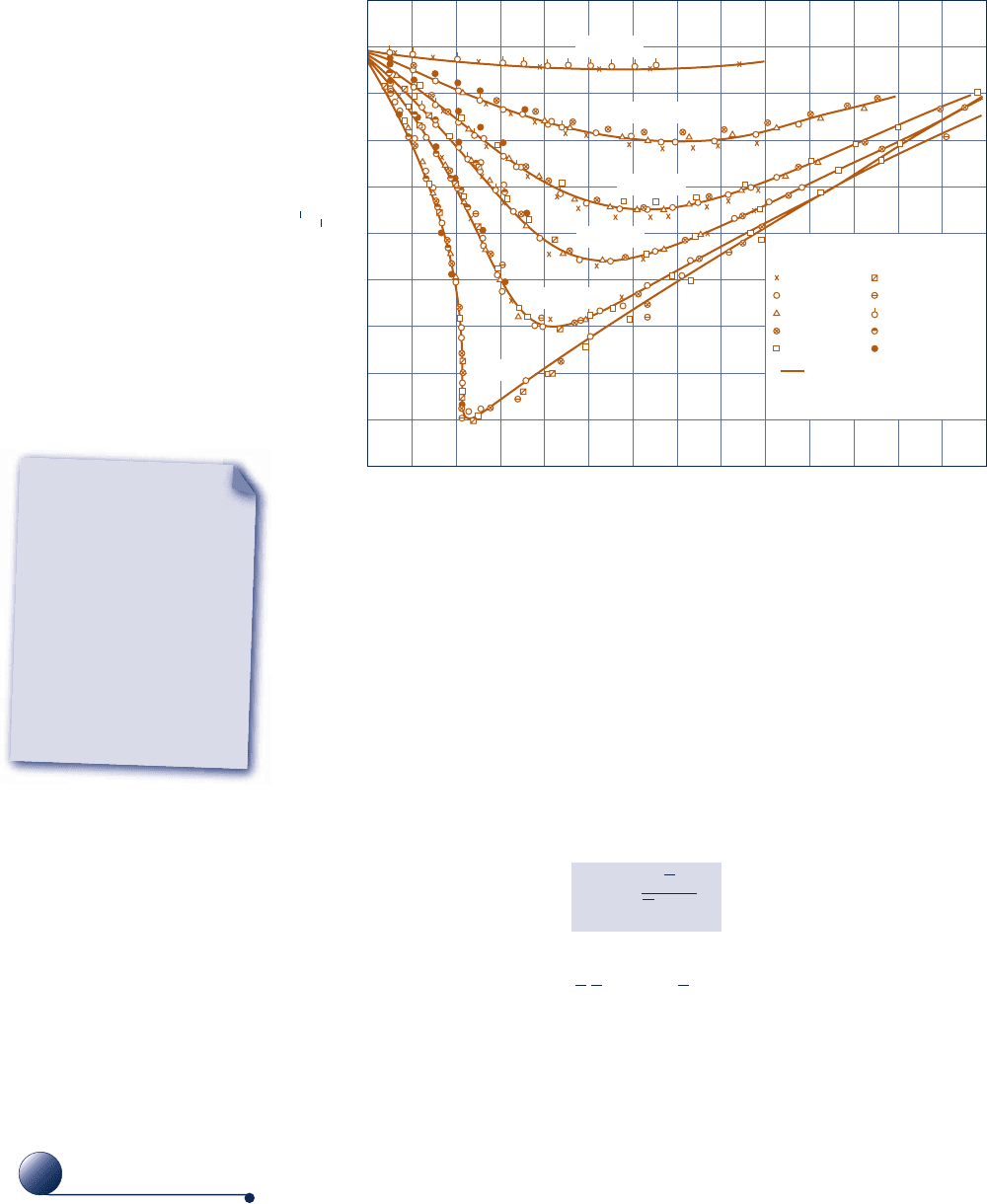
Figure 3.11 gives the compressibility factor for hydrogen versus pres-

sure at specified values of temperature. Similar charts have been pre-

pared for other gases. When these charts are studied, they are found

to be qualitatively similar. Further study shows that when the coordi-

nates are suitably modified, the curves for several different gases coin-

cide closely when plotted together on the same coordinate axes, and so quantitative

similarity also can be achieved. This is referred to as the principle of corresponding

states. In one such approach, the compressibility factor Z is plotted versus a dimen-

sionless

reduced pressure p

and reduced temperature T

, defined as

5 p

(3.27)

5 T

(3.28)

where p

and T

denote the critical pressure and temperature, respectively. This results

in a generalized compressibility chart of the form Z 5 f(p

, T

). Figure 3.12 shows

experimental data for 10 different gases on a chart of this type. The solid lines denot-

ing reduced isotherms represent the best curves fitted to the data. Observe that

Tables A-1 provide the critical temperature and critical pressure for a sampling of

substances.

1.5

1.0

0.5

0 100 200

35 K (63°R)

50 K (90°R)

60 K (108°R)

200 K (360°R)

300 K (540°R)

100 K (180°R)

p (atm)

Fig. 3.11 Variation of the compressibility

factor of hydrogen with pressure at constant

temperature.

Values of the Gas Constant R of Selected Elements and Compounds

Substance Chemical Formula R (kJ/kg

K) R (Btu/lb

8R)

Air — 0.2870 0.06855

Ammonia NH

0.4882 0.11662

Argon Ar 0.2082 0.04972

Carbon dioxide CO

0.1889 0.04513

Carbon monoxide CO 0.2968 0.07090

Helium He 2.0769 0.49613

Hydrogen H

4.1240 0.98512

Methane CH

0.5183 0.12382

Nitrogen N

0.2968 0.07090

Oxygen O

0.2598 0.06206

Water H

O 0.4614 0.11021

TABLE 3.1

Source: R values are calculated in terms of the universal gas constant R 5 8.314 kJ

kmol ? K 5 1.986 Btu

lbmol ? 8R

and the molecular weight M provided in Table A-1 using R 5 R

M (Eq. 3.25).

reduced pressure

and temperature

3.11 Generalized Compressibility Chart 123

c03EvaluatingProperties.indd Page 123 5/19/10 8:32:23 PM user-s146 c03EvaluatingProperties.indd Page 123 5/19/10 8:32:23 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

124 Chapter 3 Evaluating Properties

A generalized chart more suitable for problem solving than Fig. 3.12 is given in

the Appendix as Figs. A-1, A-2, and A-3. In Fig. A-1, p

ranges from 0 to 1.0; in

Fig. A-2, p

ranges from 0 to 10.0; and in Fig. A-3, p

ranges from 10.0 to 40.0. At

any one temperature, the deviation of observed values from those of the general-

ized chart increases with pressure. However, for the 30 gases used in developing

the chart, the deviation is at most on the order of 5% and for most ranges is much

less.

Values of specific volume are included on the generalized chart through the vari-

able y9

, called the pseudoreduced specific volume, defined by

y¿

(3.29)

The pseudoreduced specific volume gives a better correlation of the data than does

the reduced specific volume y

5 y

, where y

is the critical specific volume.

Using the critical pressure and critical temperature of a substance of interest, the

generalized chart can be entered with various pairs of the variables T

, p

, and

y 9

: (T

, p

), (p

, y9

), or (T

, y9

). The merit of the generalized chart for relating p,

y, and T data for gases is simplicity coupled with accuracy. However, the generalized

compressibility chart should not be used as a substitute for p–y–T data for a given

substance as provided by tables or computer software. The chart is mainly useful for

obtaining reasonable estimates in the absence of more accurate data.

The next example provides an illustration of the use of the generalized compress-

ibility chart.

To determine Z for hydrogen, helium, and neon above a T

of 5, the reduced temperature and pressure

should be calculated using T

5 T/(T

1 8) and p

5 p/(p

1 8), where temperatures are in K and pres-

sures are in atm.

pseudoreduced

specific volume

= 1.00

Z =

–––

1.1

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0 1.0 2.0 3.0 4.0 5.0 6.0 7.00.5 1.5 2.5 3.5 4.5 5.5 6.5

Methane

Ethylene

Ethane

Propane

n-Butane

Isopentane

n-Heptane

Nitrogen

Carbon dioxide

Water

Average curve based on

data on hydrocarbons

Legend

Reduced pressure p

= 2.00

= 1.50

= 1.30

= 1.20

= 1.10

Fig. 3.12 Generalized compressibility chart for various gases.

generalized compressibility

chart

TAKE NOTE...

Study of Fig. A-2 shows

that the value of Z tends

to unity at fixed reduced

temperature T

as reduced

pressure p

tends to zero.

That is, Z

as p

0 at fixed T

Figure A-2 also shows that

Z tends to unity at fixed

reduced pressure as reduced

temperature becomes large.

Ideal_Gas

A.15 – Tab a

c03EvaluatingProperties.indd Page 124 6/30/10 10:54:31 AM user-s146 c03EvaluatingProperties.indd Page 124 6/30/10 10:54:31 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

Using the Generalized Compressibility Chart

c c c c EXAMPLE 3.7 c

A closed, rigid tank filled with water vapor, initially at 20 MPa, 5208C, is cooled until its temperature reaches

4008C. Using the compressibility chart, determine

(a) the specific volume of the water vapor in m

/kg at the initial state.

(b) the pressure in MPa at the final state.

Compare the results of parts (a) and (b) with the values obtained from the superheated vapor table, Table A-4.

SOLUTION

Known:

Water vapor is cooled at constant volume from 20 MPa, 5208C to 4008C.

Find: Use the compressibility chart and the superheated vapor table to determine the specific volume and final

pressure and compare the results.

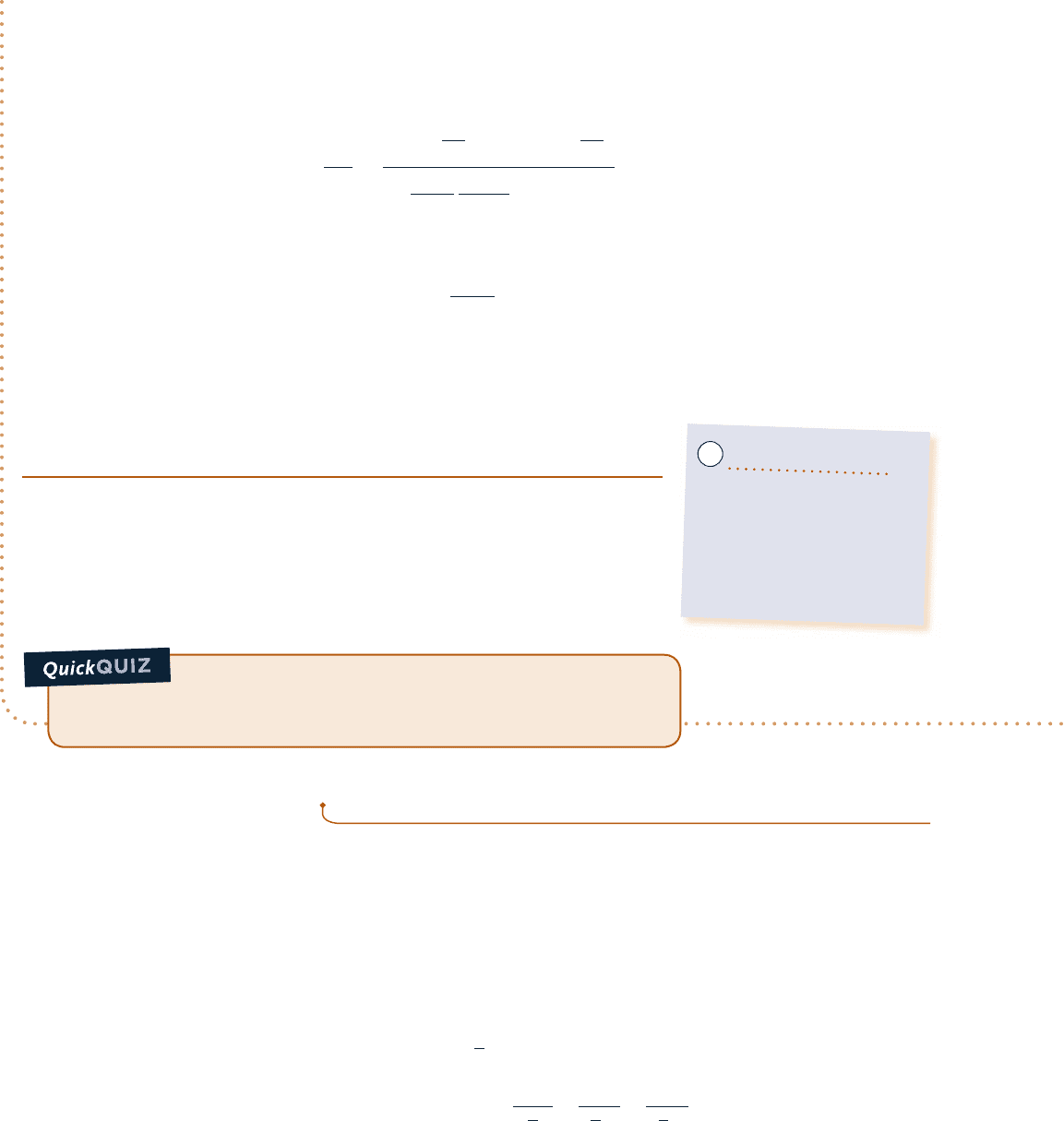
Schematic and Given Data:

Analysis:

(a) From Table A-1, T

5 647.3 K and p

5 22.09 MPa for water. Thus

➊

793

7.3

5 1.23,



.09

5 0.91

With these values for the reduced temperature and reduced pressure, the value of Z obtained from Fig. A-1 is

approximately 0.83. Since Z 5 py/RT, the specific volume at state 1 can be determined as follows:

5 Z

5 0.83

➋

5 0.83 ±

8314

N ?

kmol ? K

18.02

kmol

≤

3 K

20 3 10

5 0.0152 m

The molecular weight of water is from Table A-1.

Engineering Model:

The water vapor is

a closed system.

2. The initial and

final states are at

equilibrium.

3. The volume is

constant.

Fig. E3.7

1.0

0.5

Z =

–––

0 0.5

1.0

v´

= 1.2

v´

= 1.1

= 1.3

= 1.2

= 1.05

Water

vapor

Cooling

Block of ice

Closed, rigid tank

20 MPa

520°C

400°C

3.11 Generalized Compressibility Chart 125

c03EvaluatingProperties.indd Page 125 5/27/10 7:33:11 AM user-f391 c03EvaluatingProperties.indd Page 125 5/27/10 7:33:11 AM user-f391 /Users/user-f391/Desktop/27MAY/Users/user-f391/Desktop/27MAY

126 Chapter 3

Evaluating Properties

3.11.4

Equations of State

Considering the curves of Figs. 3.11 and 3.12, it is reasonable to think that the varia-

tion with pressure and temperature of the compressibility factor for gases might be

expressible as an equation, at least for certain intervals of p and T. Two expressions

can be written that enjoy a theoretical basis. One gives the compressibility factor as

an infinite series expansion in pressure:

Z 5 1 1 B

1T2p 1 C

1T2p

1 D

1T2p

. . .

(3.30)

where the coefficients B

, C

, D

, . . . depend on temperature only. The dots in Eq. 3.30

represent higher-order terms. The other is a series form entirely analogous to Eq. 3.30

but expressed in terms of 1

y instead of p

Z 5 1 1

B1T

C1T

D1T

. . .

(3.31)

Equations 3.30 and 3.31 are known as

virial equations of state, and the coefficients

, C

, D

, . . . and B, C, D, . . . are called virial coefficients. The word virial stems from

the Latin word for force. In the present usage it is force interactions among molecules

that are intended.

Turning to Table A-4, the specific volume at the initial state is 0.01551 m

/kg. This is in good agreement with

the compressibility chart value, as expected.

(b) Since both mass and volume remain constant, the water vapor cools at constant specific volume, and thus

at constant y9

. Using the value for specific volume determined in part (a), the constant y9

value is

y¿

a0.0152

ba22.09 3 10

831

18.02

N ? m

kg ? K

b1647.3 K2

5 1.12

At state 2

673

647.3

5 1.04

Locating the point on the compressibility chart where y9

5 1.12 and T

5 1.04, the corresponding value for p

is about 0.69. Accordingly

5 p

25 122.09 MPa210.6925 15.24 MPa

Interpolating in the superheated vapor tables gives p

5 15.16 MPa. As before,

the compressibility chart value is in good agreement with the table value.

➊ Absolute temperature and absolute pressure must be used in evaluating

the compressibility factor Z, the reduced temperature T

, and reduced

pressure p

➋ Since Z is unitless, values for p, y, R, and T must be used in consistent

units.

Using the compressibility chart, determine the specific vol-

ume, in m

/kg, for water vapor at 14 MPa, 4408C. Compare with the steam

table value. Ans. 0.0195 m

/kg

virial equations of state

Ability to…

❑

retrieve p–y–T data from the

generalized compressibility

chart.

❑

retrieve p–y–T data from

the steam tables..

✓

Skills Developed

c03EvaluatingProperties.indd Page 126 5/19/10 8:32:27 PM user-s146 c03EvaluatingProperties.indd Page 126 5/19/10 8:32:27 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

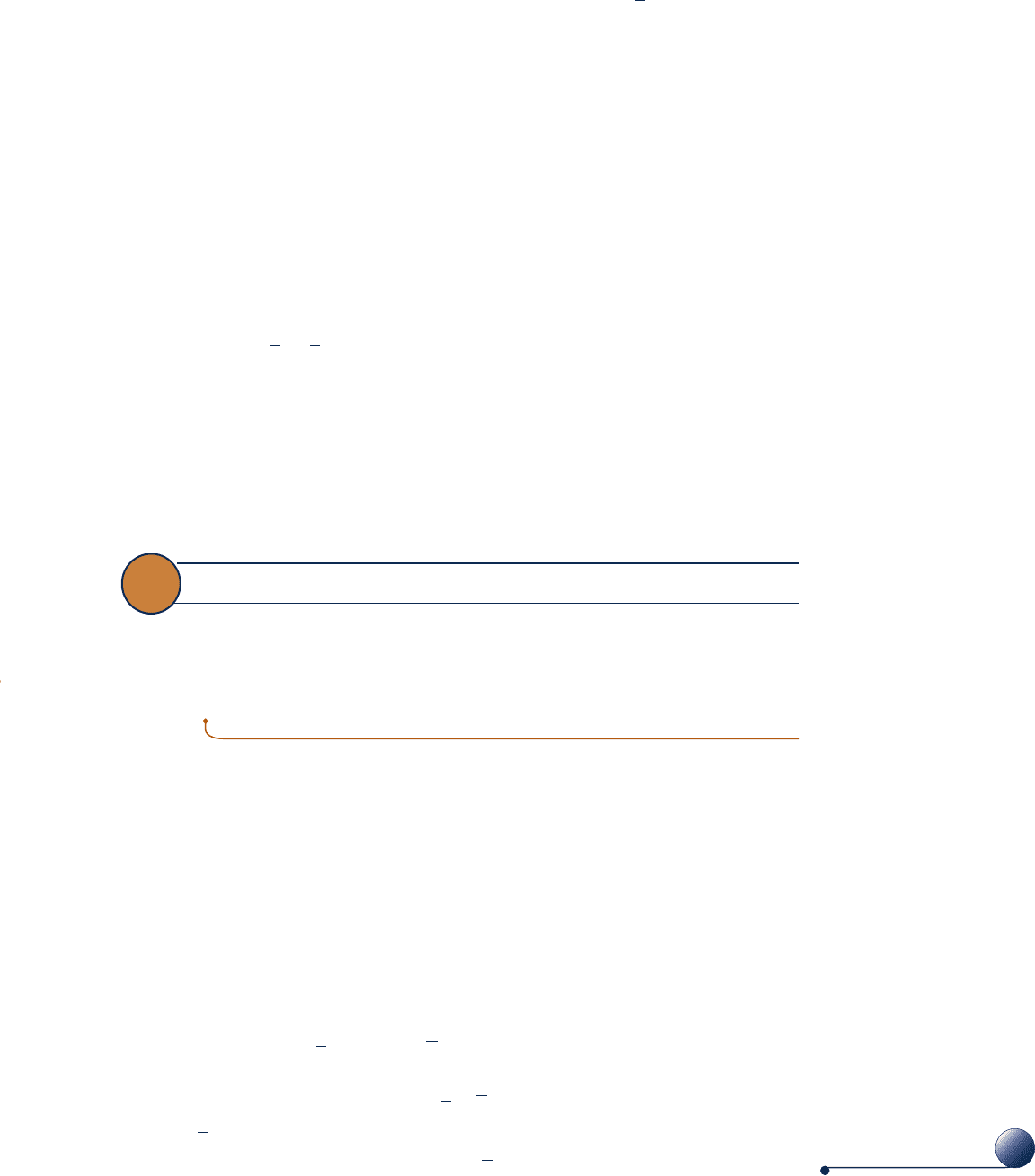
The virial expansions can be derived by the methods of statistical mechanics, and

physical significance can be attributed to the coefficients: B

y accounts for two-

molecule interactions, C

accounts for three-molecule interactions, etc. In principle,

the virial coefficients can be calculated by using expressions from statistical mechan-

ics derived from consideration of the force fields around the molecules of a gas. The

virial coefficients also can be determined from experimental p–y–T data. The virial

expansions are used in Sec. 11.1 as a point of departure for the further study of ana-

lytical representations of the p–y–T relationship of gases known generically as equa-

tions of state.

The virial expansions and the physical significance attributed to the terms making

up the expansions can be used to clarify the nature of gas behavior in the limit as

pressure tends to zero at fixed temperature. From Eq. 3.30 it is seen that if pressure

decreases at fixed temperature, the terms B

p, C

, etc. accounting for various molec-

ular interactions tend to decrease, suggesting that the force interactions become

weaker under these circumstances. In the limit as pressure approaches zero, these

terms vanish, and the equation reduces to Z 5 1 in accordance with Eq. 3.26. Simi-

larly, since specific volume increases when the pressure decreases at fixed tempera-

ture, the terms B

y , C

, etc. of Eq. 3.31 also vanish in the limit, giving Z 5 1 when

the force interactions between molecules are no longer significant.

Evaluating Properties Using

the Ideal Gas Model

3.12 Introducing the Ideal Gas Model

In this section the ideal gas model is introduced. The ideal gas model has many applica-

tions in engineering practice and is frequently used in subsequent sections of this text.

3.12.1

Ideal Gas Equation of State

As observed in Sec. 3.11.3, study of the generalized compressibility chart Fig. A-2

shows that at states where the pressure p is small relative to the critical pressure p

(low p

) and/or the temperature T is large relative to the critical temperature T

(high

), the compressibility factor, Z 5 py/RT, is approximately 1. At such states, we can

assume with reasonable accuracy that Z 5 1, or

py 5 RT (3.32)

Known as the ideal gas equation of state, Eq. 3.32 underlies the second part of this

chapter dealing with the ideal gas model.

Alternative forms of the same basic relationship among pressure, specific volume,

and temperature are obtained as follows. With y 5 V/m, Eq. 3.32 can be expressed as

pV 5 mRT (3.33)

In addition, using y 5 y

M and R 5 R

M, which are Eqs. 1.9 and 3.25, respectively,

where M is the molecular weight, Eq. 3.32 can be expressed as

5 RT (3.34)

or, with y 5 V

n, as

pV 5 nRT (3.35)

ideal gas equation

of state

3.12 Introducing the Ideal Gas Model 127

Ideal_Gas

A.15 – Tab b

c03EvaluatingProperties.indd Page 127 6/30/10 10:56:09 AM user-s146 c03EvaluatingProperties.indd Page 127 6/30/10 10:56:09 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

128 Chapter 3 Evaluating Properties

3.12.2

Ideal Gas Model

For any gas whose equation of state is given exactly by p

5 RT, the specific internal

energy depends on temperature only. This conclusion is demonstrated formally in Sec.

11.4. It is also supported by experimental observations, beginning with the work of

Joule, who showed in 1843 that the internal energy of air at low density (large specific

volume) depends primarily on temperature. Further motivation from the microscopic

viewpoint is provided shortly. The specific enthalpy of a gas described by p

5 RT

also depends on temperature only, as can be shown by combining the definition of

enthalpy, h 5 u 1 p

, with u 5 u(T) and the ideal gas equation of state to obtain

h 5 u(T) 1 RT. Taken together, these specifications constitute the ideal gas model,

summarized as follows

y 5 RT (3.32)

u 5 u1T2 (3.36)

h 5 h1T25 u1T21 RT (3.37)

The specific internal energy and enthalpy of gases generally depend on two

independent properties, not just temperature as presumed by the ideal gas model.

Moreover, the ideal gas equation of state does not provide an acceptable approx-

imation at all states. Accordingly, whether the ideal gas model is used depends on

the error acceptable in a given calculation. Still, gases often do approach ideal gas

behavior, and a particularly simplified description is obtained with the ideal gas

model.

To verify that a gas can be modeled as an ideal gas, the states of interest can be

located on a compressibility chart to determine how well Z 5 1 is satisfied. As shown

in subsequent discussions, other tabular or graphical property data can also be used

to determine the suitability of the ideal gas model.

The next example illustrates the use of the ideal gas equation of state and rein-

forces the use of property diagrams to locate principal states during processes.

ideal gas model

Analyzing Air as an Ideal Gas Undergoing a Thermodynamic Cycle

c c c c EXAMPLE 3.8 c

One pound of air in a piston–cylinder assembly undergoes a thermodynamic cycle consisting of three processes.

Process 1–2: Constant specific volume

Process 2–3: Constant-temperature expansion

Process 3–1: Constant-pressure compression

At state 1, the temperature is 5408R, and the pressure is 1 atm. At state 2, the pressure is 2 atm. Employing the

ideal gas equation of state,

(a) sketch the cycle on p–y coordinates.

(b) determine the temperature at state 2, in 8R.

/lb.

SOLUTION

Known:

Air executes a thermodynamic cycle consisting of three processes: Process 1–2, y 5 constant; Process

2–3, T 5 constant; Process 3–1, p 5 constant. Values are given for T

, p

, and p

TAKE NOTE...

To expedite the solutions of

many subsequent examples

and end-of-chapter problems

involving air, oxygen (O

nitrogen (N

), carbon dioxide

(CO

), carbon monoxide (CO),

hydrogen (H

), and other

common gases, we indicate

in the problem statements

that the ideal gas model

should be used. If not

indicated explicitly, the suit-

ability of the ideal gas model

should be checked using the

Z chart or other data.

c03EvaluatingProperties.indd Page 128 7/1/10 7:17:52 AM user-s146 c03EvaluatingProperties.indd Page 128 7/1/10 7:17:52 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

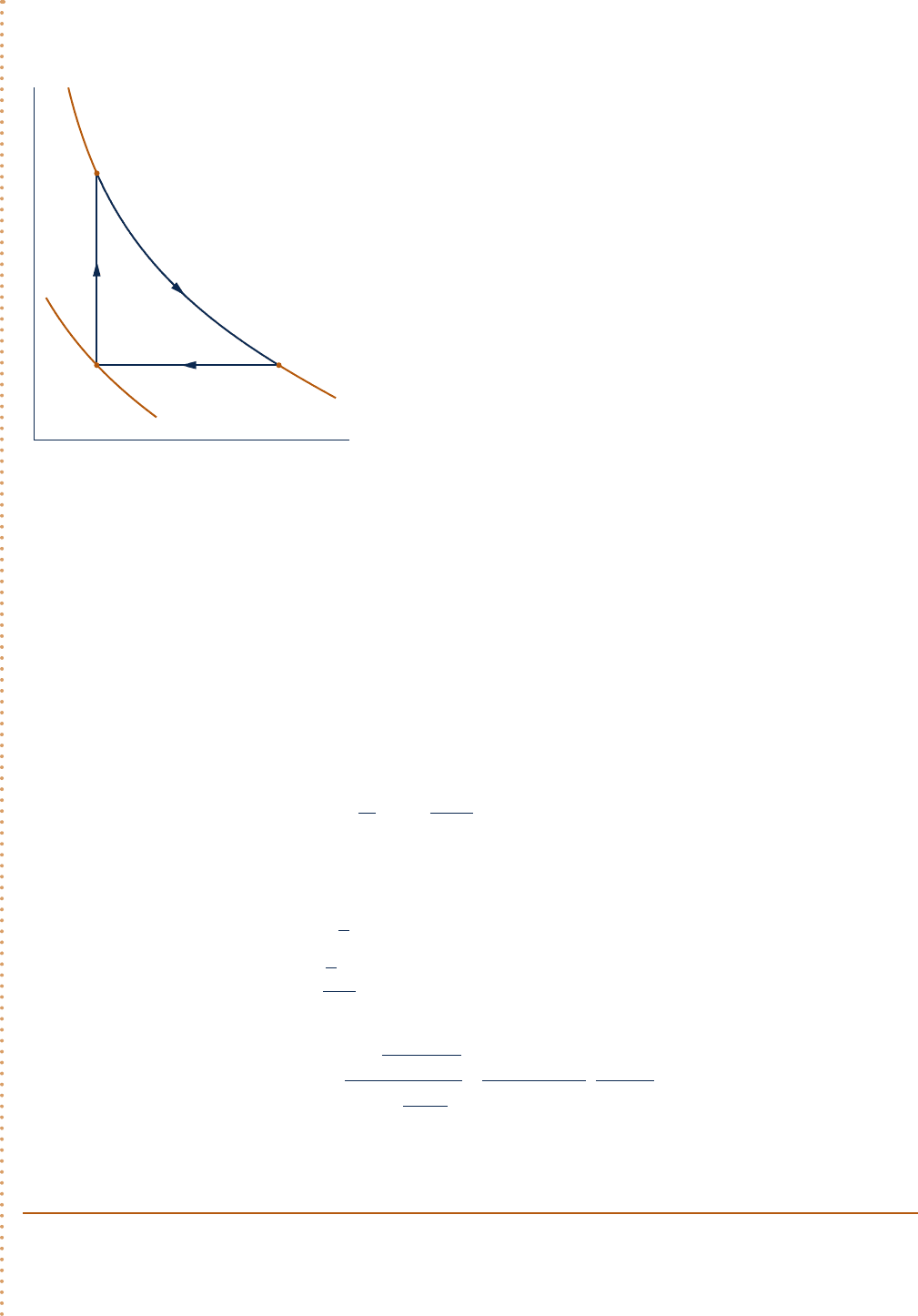
Find: Sketch the cycle on p–y coordinates and determine T

and y

Schematic and Given Data:

Engineering Model:

1. The air is a closed system.

➊ 2. The air behaves as an ideal gas.

3. The piston is the only work mode.

= 1 atm

= 2 atm

T = C

v = C

p = C

1080°R

540°R

Fig. E3.8

Analysis:

(a) The cycle is shown on p–y coordinates in the accompanying figure. Note that since p 5 RT/y and tempera-

ture is constant, the variation of p with y for the process from 2 to 3 is nonlinear.

(b) Using py 5 RT, the temperature at state 2 is

5 p

To obtain the specific volume y

required by this relationship, note that y

5 y

, so

➋ y

5 RT

Combining these two results gives

2 atm

1 atm

15408R25 10808R

5 RT

Noting that T

5 T

, p

5 p

, and

5 R

1545

ft ? lbf

lbmol ? 8R

28.97

lbmol

≤

110808R2

114.7 lbf

in.

1 ft

144 in.

5 27.2 ft

where the molecular weight of air is from Table A-1E.

3.12 Introducing the Ideal Gas Model 129

c03EvaluatingProperties.indd Page 129 5/27/10 7:57:05 AM user-f391 c03EvaluatingProperties.indd Page 129 5/27/10 7:57:05 AM user-f391 /Users/user-f391/Desktop/27MAY/Users/user-f391/Desktop/27MAY

130 Chapter 3 Evaluating Properties

3.12.3

Microscopic Interpretation

A picture of the dependence of the internal energy of gases on temperature at low

density (large specific volume) can be obtained with reference to the discussion of

the virial equations: Eqs. 3.30 and 3.31. As p S 0

y S q

, the force interactions

between molecules of a gas become weaker, and the virial expansions approach Z 5 1

in the limit. The study of gases from the microscopic point of view shows that the

dependence of the internal energy of a gas on pressure, or specific volume, at a

specified temperature arises primarily because of molecular interactions. Accordingly,

as the density of a gas decreases (specific volume increases) at fixed temperature,

there comes a point where the effects of intermolecular forces are minimal. The

internal energy is then determined principally by the temperature.

From the microscopic point of view, the ideal gas model adheres to several ideal-

izations: The gas consists of molecules that are in random motion and obey the laws

of mechanics; the total number of molecules is large, but the volume of the molecules

is a negligibly small fraction of the volume occupied by the gas; and no appreciable

forces act on the molecules except during collisions. Further discussion of the ideal

gas using the microscopic approach is provided in Sec. 3.13.2.

➊ Table A-1E gives p

5 37.2 atm, T

5 2398R for air. Therefore, p

5 0.054,

5 4.52. Referring to Fig. A-1, the value of the compressibility factor at

this state is Z

1. The same conclusion results when states 1 and 3 are

checked. Accordingly, py 5 RT adequately describes the p–y–T relation for

the air at these states.

➋ Carefully note that the equation of state py 5 RT requires the use of abso-

lute temperature T and absolute pressure p.

Is the cycle sketched in Fig. E3.8 a power cycle or a refrigera-

tion cycle? Explain. Ans. A power cycle. As represented by enclosed area

1-2-3-1, the net work is positive.

Ability to…

❑

evaluate p–y–T data using the

ideal gas equation of state.

❑

sketch processes on a p–y

diagram

✓Skills Developed

3.13 Internal Energy, Enthalpy, and Specific

Heats of Ideal Gases

3.13.1

Du, Dh, c

, and c

Relations

For a gas obeying the ideal gas model, specific internal energy depends only on tem-

perature. Hence, the specific heat c

, defined by Eq. 3.8, is also a function of temperature

alone. That is,

1T25



1ideal gas2

(3.38)

This is expressed as an ordinary derivative because u depends only on T.

By separating variables in Eq. 3.38

du 5 c

dT (3.39)

c03EvaluatingProperties.indd Page 130 5/19/10 8:32:32 PM user-s146 c03EvaluatingProperties.indd Page 130 5/19/10 8:32:32 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

On integration, the change in specific internal energy is

u1T

22 u1T

1T2 dT



1ideal gas2

(3.40)

Similarly, for a gas obeying the ideal gas model, the specific enthalpy depends only

on temperature, so the specific heat c

, defined by Eq. 3.9, is also a function of tem-

perature alone. That is

1T25



1ideal gas2

(3.41)

Separating variables in Eq. 3.41

dh 5 c

dT (3.42)

On integration, the change in specific enthalpy is

h1T

22 h1T

1T2 dT



1ideal gas2

(3.43)

An important relationship between the ideal gas specific heats can be developed

by differentiating Eq. 3.37 with respect to temperature

1 R

and introducing Eqs. 3.38 and 3.41 to obtain

5 c

1 R



ideal gas

(3.44)

On a molar basis, this is written as

1T25 c

1T21 R



1ideal gas2 (3.45)

Although each of the two ideal gas specific heats is a function of temperature,

Eqs. 3.44 and 3.45 show that the specific heats differ by just a constant: the gas constant.

Knowledge of either specific heat for a particular gas allows the other to be calculated

by using only the gas constant. The above equations also show that c

. c

and c

. c

respectively.

For an ideal gas, the specific heat ratio, k, is also a function of temperature only

k 5



1ideal gas2

(3.46)

Since c

. c

, it follows that k . 1. Combining Eqs. 3.44 and 3.46 results in

1T25

2 1

(3.47a)

(ideal gas)

1T25

2 1

(3.47b)

Similar expressions can be written for the specific heats on a molar basis, with R being

replaced by

3.13 Internal Energy, Enthalpy, and Specific Heat of Ideal Gases 131

c03EvaluatingProperties.indd Page 131 5/19/10 8:32:33 PM user-s146 c03EvaluatingProperties.indd Page 131 5/19/10 8:32:33 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

132 Chapter 3

Evaluating Properties

3.13.2

Using Specific Heat Functions

The foregoing expressions require the ideal gas specific heats as functions of tem-

perature. These functions are available for gases of practical interest in various

forms, including graphs, tables, and equations. Figure 3.13 illustrates the variation

of c

(molar basis) with temperature for a number of common gases. In the range

of temperature shown, c

increases with temperature for all gases, except for the

monatonic gases Ar, Ne, and He. For these, c

is constant at the value predicted by

kinetic theory: c

R. Tabular specific heat data for selected gases are presented

versus temperature in Tables A-20. Specific heats are also available in equation

form. Several alternative forms of such equations are found in the engineering

literature. An equation that is relatively easy to integrate is the polynomial form

5 a 1 bT 1 gT

1 dT

1 eT

(3.48)

Values of the constants a, b, g, d, and e are listed in Tables A-21 for several gases in

the temperature range 300 to 1000 K (540 to 18008R).

to illustrate the use of Eq. 3.48, let us evaluate the change in spe-

cific enthalpy, in kJ/kg, of air modeled as an ideal gas from a state where T

5 400 K

to a state where T

5 900 K. Inserting the expression for c

1T2 given by Eq. 3.48 into

Eq. 3.43 and integrating with respect to temperature

2 h

1a 1 bT 1 gT

1 dT

1 eT

2dT

a1T

2 T

1000

1000 2000 3000

2000 3000 4000 5000

Temperature, °R

Temperature, K

Air

Ar, Ne, He

Fig. 3.13 Variation of

---

----

R with temperature for a number of gases modeled

as ideal gases.

c03EvaluatingProperties.indd Page 132 5/19/10 8:32:34 PM user-s146 c03EvaluatingProperties.indd Page 132 5/19/10 8:32:34 PM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New