Могилев А.В., Пак Н.И., Хённер Е.К. Информатика

Подождите немного. Документ загружается.

Uses Crt; Var I, N : Longint; X, Y : Real;

Begin

Randomize; N := 0;

For I := 1 To 100000 Do

Begin

X := Random; Y := Random;

If Sqr(X - 0.5) + Sqr(Y - 0.5) < 0.25 Then N := N + 1

End;

WriteLn ('pi=', (N / 100000 / Sqr(0.5)) : 8 : 5) ;

Repeat Until KeyPressed End.

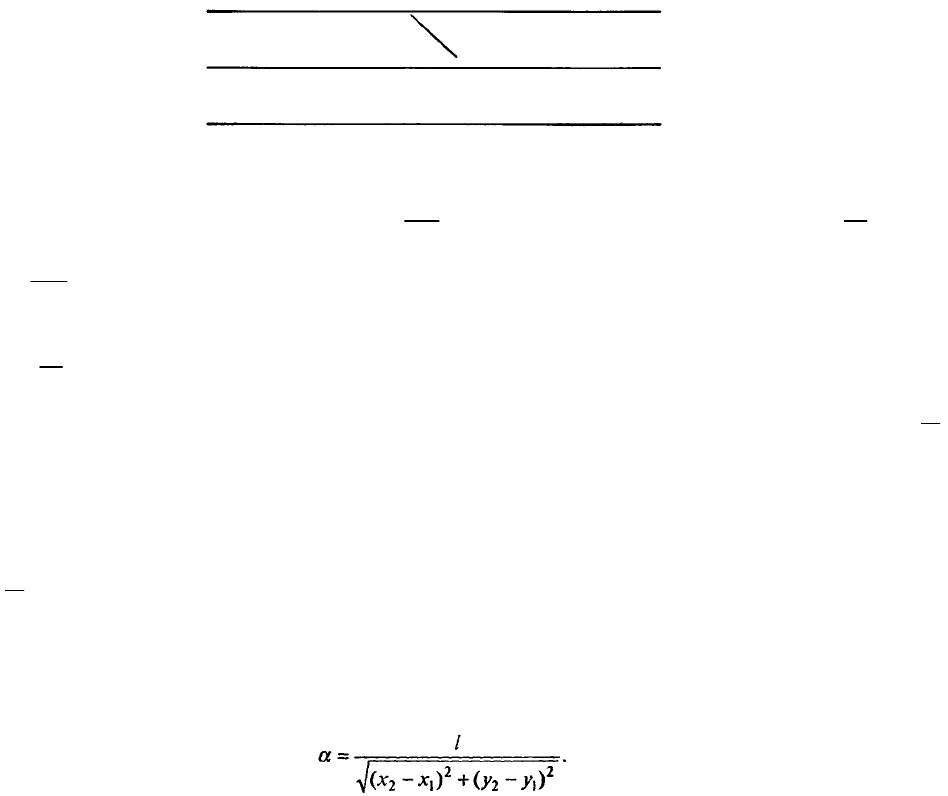
2. Задача Бюффона. На поле, разграфленное параллельными прямыми, расстояние между

которыми L, бросается наугад игла длиной l (рис. 7.60). Какова вероятность того, что игла, упав,

пересечег хотя бы одну прямую?

Рис. 7.60. К. задаче Бюффона

Ж.Бюффон (XVIII в.) подсчитал: р =



. Таким образом, если L = 2l, то р =



. Кроме

того, р =

, где N - число бросаний, N

- число пересечений иглы с линиями.

Относительная доля случаев, когда игла пересечет хотя бы одну из параллельных прямых

равно р =



. Это был один из старинных способов опредения числа π.

Имитационное моделирование проведем следующим образом. Примем L = 1 и l =

«Иглу» будем «бросать» в квадрат размером, скажем, 20х20, левый нижний угол которого имеет

координаты (0, 0). Положение концов иглы будем задавать с помощью датчика равномерно

распределенные, случайных чисел в диапазоне от 0 до 20. Точнее говоря, эти числа определят

направление отрезка, вдоль которого находится очередная игла; для того, чтобы ее длина была

равна

, вторую из случайных точек - концов отрезка - подвинем вдоль него до достижения

указанной длины иглы. В математическом отношении это сводится к следующей несложной

процедуре;

• генерация координат точек А(х

, y

), B(x

, у

);

• определение координат точки В

(х

+ α(х

– х

), у

+ α(у

– у

)), где

Поскольку расстояние между горизонтальными линиями взято равным единице, а сами

линии имеют целочисленные координаты по у, то определить, пересекает ли игла прямую, очень

просто - да, если целые части ординат тoчeк A и В

различны.

Программа 155 Решение задачи Бюффона.

Program Buffon;

Uses Crt; Var I, J, K, M, N : Integer; XI, X2, Y1, Y2, Al : Real;

Begin

Randomize; M := 30000; N := 1;

For I := 1 To M Do

Begin

X1 := Random * 20; Yl := Random * 20; X2 := Random * 20;

Y2 := Random * 20;

671

A1 := 0.5 / Sqrt(Sqr(X2 – X1) + Sqr(Y2 - Yl) ) ;

J := Round(Yl); К := Round(Yl + A1 * (Y2 – Y1));

If J <> К Then N := H + 1

End;

WriteLn('pi=', W / N) : 8 : 5); Repeat Until KeyPressed

End.

Создание демонстрационной программы, которая выводит на экран несколько

параллельных прямых из общего набора и имеющие к ним отношение «иглы», предоставляем

читателю.

Рекомендуем провести с предложенной программой несколько экспериментов. Понятно,

что чем больше значение т, тем, по-видимому, точнее результат. Однако. почему он постоянно

слегка занижен? Все ли учтено на краях той зоны, в которой разыгрываются броски иглы? Чтобы

почувствовать проблему, следует увеличить число параллельных прямых, что в данной программе

очень легко сделать. Почему результат становится лучше? Отметим, что проблема краевых

условий, когда события должны по условиям задачи разыгрываться на бесконечном поле, а при

имитационном моделировании фактически разыгрываются на конечном (и даже не очень

большом), возникает часто и решение ее нетривиально.

3. Нефтяное месторождение. Дано нефтяное месторождение, в котором область залегания

нефти G ограничивается кривой С. Дебит скважины, т.е. количество получаемой из нее нефти в

единицу времени, зависит от пластового давления нефти U в точке скважины. Поэтом) для

прогнозирования нефтедобычи важно знать распределение пластового давления на всем

месторождении при условии, что оно экспериментально измерено лишь на его границе. В

математическом плане функция U(r) удовлетворяет уравнению Лапласа

)(

rU

= 0; задача

нахождения его решения внутри области при заданном значении U(r) на границе - так называемая,

краевая задача Дирихле; в данной задаче это решение, которое часто совсем не просто найти

аналитически, позволило бы правильно определить точку для скважины.

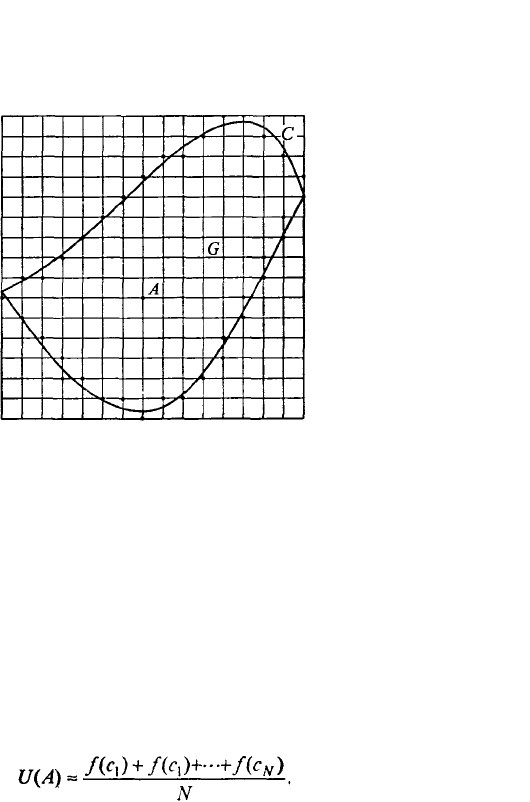
Рис. 7.61. Наложение сетки на заданную область

Покроем область G мелкой сеткой. Отметим узлы, наиболее близкие к границе С, и будем

считать, что значения функции U в этих узлах приблизительно равны значениям этой функции в

ближайших к ним точках границы. Будем искать значение функции U(A) в некотором внутреннем

узле A (рис. 7.61).

Поместим в точке А блуждающую частицу, которая может перемещаться по области в

последовательные моменты времени, переходя из одного угла в соседний. Направления

перемещений случайны, равновероятны и не зависят от ее положения и предыстории блуждания.

Случайный эксперимент состоит в наблюдении факта выхода блуждающей частицы в некоторый

граничный узел. Когда блуждание прекращается, запоминается значение функции f(с

) в этой

точке, и так далее, N раз. Замечательный факт состоит в том, что решение в точке

Другими словами, среднее значение приближенно равно решению задачи Дирихле в точке

А.

4. Модель «пьяницы» (модель случайного блуждания). Зададим блуждание точки

672

(объекта) по горизонтальной линии по правилу: если случайное число из интервала [0, 1] меньше

0,5, то точка делает шаг вправо x = х + h, в противном случае x = х - h.

Программа 156. Модель случайного блуждания

Program Tochka;

Uses Crt, Graph; Var I, J : Integer; Z, P, X, H, Y : Integer;

Begin

X := 320; Y := 240; H := 10; P := 4; DetectGraph(I, J) ;

InitGraphd, J, ");

SetColor(15); Line(10, 312, 630, 312); Randomize;

Repeat

Z := Random(8); If Z >= P Then X := X + H Else X := X - H;

SetColor(Green); Circle(X, Y, 10); Delay(200);

SetColor(0); Circle(X, Y, 10)

Until KeyPressed Or (X >= 640) Or (X <= 0); CloseGraph

End.

В программе шаг является постоянным, но никто не мешает нам сделать его переменным,

выбирая из интервала [0, hmax] случайным образом. Для этого зададим максимально возможный

шаг НМах и в цикле определим H := Random(HMax).

Если задать аналогичным образом вероятности движения точки вверх – вниз, вправо -

влево (0 < рх < 1, 0 < рy < 1), получим хаотическое блуждание точки на плоскости. Для

моделирования блуждания точки в замкнутом прямоугольном объеме примем абсолютно упругое

(зеркальное) отражение от стенок.

Программа 157. Хаотическое блуждание точки

Program Broun;

Uses Crt, Graph;

Var I, J, X, Y, HxMax, HyMax, Hx, Ну : Integer; PI, P2, Z1, Z2 : Real;

Begin

X := 320; Y :== 240; HxMax := 30; PI := 0.5; P2 := 0.5; HyMax := 30;

DetectGraph (I, J) ; InitGraph (1, J, ''); SetColor(15);

Randomize; RectAngle(100, 100, 540, 380);

SetColor(Green); Circle(X, Y, 10); Delay(200); SetColor(0);

Circle(X, У, 10);

Repeat

Zl := Random; Z2 := Random; Hx := Random(HxMax);

Ну := Random(HyMax) ;

If (Zl < PI) Then X := X + Hx Else X := X - Hx;

If (Z2 < P2) Then Y := Y + Ну Else Y :" У - Ну;

If X <= 110 Then X := X + 2 * (110 - X) ;

If X >= 530 Then X := X - 2 * (-530 + X) ;

If Y <= 110 Then Y := Y + 2 * (110 - Y) ;

If Y >= 370 Then Y := Y - 2 * (Y - 370);

SetColor(Green); Circle(X, Y, 10); Delay(100);

SetColor(0); Circle(X, Y, 10)

Until Keypressed; CloseGraph

End.

Подобным (хотя и более сложным) образом происходит броуновское движение, хорошо

известное из курса физики. Если след точки не стирать, то можно будет наблюдать на экране

траекторию такого движения. Нет большого труда перейти к случаю п частиц. Для этого

необходимо завести два массива координат точек и аналогично предыдущему примеру

организовать их движение.

Программа 158. Броуновское движение

Program Gaz;

673

Uses Crt, Graph;

Var I, J, HxMax, HyMax, Hx, Ну, N, I : Integer;

X, Y : Array[0..500] Of Integer; PI, P2, Z1, Z2 : Real;

Begin N := 100;

For I := 1 To N Do Begin X[I] := 320; Y[I] := 240 End;

HxMax := 10; PI := 0.5; P2 := 0.5; HyMax := 10;

DetectGraph (1, J) ; InitGraphd, J, ' '); SetColor(15);

Randomize; RectAngle(100, 100, 540, 380);

For I := 1 To N Do PutPixel(X[I], Y[I], White); Delay(200);

For I := 1 To N Do PutPixel(X(I], Y[I], 0) ;

Repeat

For I := 1 To N Do

Begin

Zl := Random; Z2 := Random;

Hx := Random(HxMax); Ну := Random(HyMax);

If Zl < PI Then X[I] := X[I] + Hx Else X[I] := X[I]— Hx;

If Z2 < P2 Then Y[I] := Y[I] + Ну Else Y[I] := Y[I] - Ну;

If X[I] <= 110 Then X[I] := X[I] + 2 * (110 - X[I]);

If X(I] >= 530 Then X[I] := X[I] - 2 * (-530 + Х[I];

If Y[I] <= 110 Then Y(I] := Y[I] + 2 * (110 - Y[I]);

If Y[I] >= 370 Then Y[I] := Y[I] - 2 * (Y[I] - 370);

PutPixel (X[I], Y[I], 15)

End; Delay(100);

For I := 1 To N Do PutPixel(X[I], Y[I], 0)

Until KeyPressed; CloseGraph

End.

Построенная компьютерная модель в первом приближении может позволить моделировать

многие явления и процессы, происходящие в газах: рассеивание облака, диффузия газов. С ее

помощью можно получить многие зависимости параметров газа друг от друга. В частности,

давление (число соударений частиц на стенки) от длины свободного пробега (величин HxMax и

HyMax) или от числа частиц.

Представляет значительный интерес имитационное моделирование явлений в сплошных

средах, удовлетворяющих законам идеального газа, таких, как истечение газа в вакуум, ударная

волна, волны разрежения и т.п. Для модернизации модели можно ввести в алгоритм упругое

столкновение частиц друг с другом, возникновение кластерных ансамблей и многое другое.

При вероятностном моделировании используют различные методы, которые позволяют

решать задачи из различных областей. Ниже перечислены сферы применения вероятностных

методов.

Метод статистического моделирования: решение краевых задач математической физики,

решение систем линейных алгебраических уравнений, обращение матриц и сводящиеся к ним

сеточные методы решения систем дифференциальных уравнений, вычисление кратных

интегралов, решение интегральных и интегродифференциальных уравнений, задач ядерной

физики, газовой динамики, фильтрации, теплотехники.

Метод имитационного моделирования: моделирование систем массового обслуживания,

задачи АСУ, АСУП и АСУТП, задачи защиты информации, моделирование сложных игровых

ситуаций и динамических систем.

Метод стохастической аппроксимации: рекуррентные алгоритмы решения задач

статистического оценивания.

Метод случайного поиска: решение задач оптимизации систем, зависящих от большого

числа параметров, нахождение экстремумов функции большого числа переменных.

Другие методы: вероятностные методы распознавания образов, модели адаптации,

обучения и самообучения.

Контрольные вопросы и задания

Для ответов на эти вопросы может понадобиться выход за пределы кратких сведений,

изложенных в данном параграфе.

674

1. Какие случайные события называют достоверными? невозможными? несовместимыми?

противоположными?

2. Дайте классическое определение вероятности случайного события.

3. В чем заключаются теоремы сложения и умножения вероятностей?

4. Сформулируйте локальную и интегральную теоремы Лапласа для вероятности появления

заданного числа случайных событий.

5. Сформулируйте теорему Бернулли для оценки частоты появления случайных событий

при независимых повторных испытаниях.

6. Что такое случайная величина дискретная? непрерывная?

7. Дайте определение функции распределения непрерывной случайной величины и

плотности распределения.

8. Что такое математическое ожидание и дисперсия случайной величины (при дискретном и

при непрерывном распределениях)?

9. Какое распределение называется нормальным? В чем особая значимость нормального

распределения в теории вероятностей?

10. Что такое независимая повторная выборка? Как находятся выборочные средние?

выборочные дисперсии? В каких связях они с математическим ожиданием и дисперсией

случайной величины?

11. Как построить гистограмму выборочного распределения случайной величины? Как по

ней судить о функции распределения?

12. Какими свойствами должна обладать точечная оценка параметров функции

распределения?

13. Как оценить отклонение выборочного среднего от математического ожидания при

малом числе испытаний? при большом числе испытаний? Что такое доверительный интервал?

14. Сформулируйте один из критериев согласия эмпирической и теоретической функций

распределения.

15. Что такое «случайное число»? Сформулируйте метод компьютерной генерации

последовательности равномерно распределенных псевдослучайных чисел.

16. Сформулируйте один из методов генерации последовательности псевдослучайных

чисел с заданным законом распределения.

17. Как формулируются задачи теории массового обслуживания?

18. Какие случайные процессы являются исходными (входными) для обсуждаемой в тексте

задачи? Каковы их характеристики?

19. Какие случайные процессы являются объектом исследования (выходными процессами)

для обсуждаемой в тексте задачи?

20. Как промоделировать пуассоновский процесс - входной поток клиентов в очередь?

21. Что такое «марковские» случайные процессы и являются ли исследуемые в данном

параграфе процессы «марковскими»?

22. С чем связано в первой из приведенных выше программ ограничение на объем

выборки? Можно ли его преодолеть и какими способами?

23. Может ли данная программа сделаться несостоятельной при очень большом объеме

выборки? Как преодолеть проблему, связанную с периодичностью датчика псевдослучайных

чисел?

24. Изучите распределения длительности ожидания в очереди и длительности простоя

«продавца» и соответственно средние времена ожидания в системе с одним «прилавком» при

различных комбинациях распределений промежутков времен между приходами «покупателей» и

времен обслуживания, используя следующие распределения: а) равновероятное; б) пуассоновское;

в) нормальное.

25. Выполняя задание 24, возьмите одну из рекомендованных комбинаций параметров и так

варьируйте параметр, задающий одно из распределений, чтобы выяснить его критическое

значение, переход через которое приводит к неограниченному росту очереди.

26. На междугородной телефонной станции несколько телефонисток обслуживают общую

очередь заказов. Очередной заказ обслуживает та телефонистка, которая первой освободилась.

Смоделируйте эту ситуацию, обдумайте возникающие проблемы.

27. Пусть на телефонной станции используется обычная система отказа: если абонент занят

675

(и не подключена система «ждите ответа»), очередь не формируется, и необходимо набрать номер

вновь. Допустим, что несколько абонентов пытаются связаться с одним и тем же адресатом и в

случае успеха разговаривают с ним некоторое (случайное, но не более 3 минут) времяю

Смоделируйте ситуацию. Какова вероятность того, что некто, пытающийся дозвониться, не

сможет сделать это за определенное время Т?

28. Одна ткачиха обслуживает несколько ткацких станков, осуществляя по мере неполадок

краткосрочное вмешательство, длительность которого - случайная величина. Какова вероятность

простоя сразу нескольких станков? Как велико среднее время простоя одного станка? Если

задействованы две работницы, что выгоднее: поручить каждой по отдельной группе станков или

обеим сдвоенную группу?

29. Разработайте модель перемешивания (диффузии) газов в замкнутом сосуде и

осуществите моделирование с целью изучения закономерностей процесса (зависимости ширины

зоны диффузии от числа частиц в газах, их скорости, длины свободного пробега).

30. Разработайте модель поведения газа в плоском канале с поршнем. Рассмотрите случаи

вдвижения и выдвижения поршня в замкнутом канале. Изучите поведение ударной волны в

зависимости от параметров газа (числа частиц, их скорости, длины свободного пробега)

31 Разработайте модель истечения газа из трубы.

32. Создайте модель «пчелиного роя».

33. Придумайте модель случайного блуждания точки в заданном лабиринте.

34. Предложите модель формирования очереди на стоянке такси.

35. Рассчитайте модель автобусного маршрута с h остановками.

36. Смоделируйте работу продовольственного магазина.

37. Опишите модель автозаправочной станции.

§7. КОМПЬЮТЕРНОЕ МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В ЭКОНОМИКЕ

7.1. ПОСТАНОВКА ЗAДAЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

В последние годы мы особенно отчетливо ощутили, что нет ничего важнее для общества,

чем здоровая экономика Научное исследование основ функционирования экономики - сложная и

интересная деятельность. Математические методы в ней играют возрастающую с каждым

десятилетием роль, а реализация возникающих при этом математических моделей и получение

практически важных результатов невозможны без ЭВМ.

В данном параграфе рассматривается лишь один из разделов - оптимальное планирование -

и внутри него одна из моделей, так называемое, линейное программирование. Это связано с

относительной простотой и ясностью как содержательной постановки соответствующих задач, так

и методов решения. О таких интересных, но более сложных проблемах, как выпуклое

программирование, динамическое программирование, теория игр мы лишь упомянем, отсылая

читателей за подробностями к специальной литературе. Отметим еще, что термин

«программирование» в названии этих разделов теории оптимального планирования весьма

условен, связан с историческими обстоятельствами и к программированию в общепринятом

сейчас смысле прямого отношения не имеет.

Общеизвестно, сколь важно для решения экономических задач планирование -как при

рыночной, так и при плановой экономике. Обычно для решения экономической проблемы

существует много способов (стратегий), отнюдь не равноценных по затратам финансов, людских

ресурсов, времени исполнения, а также по достигаемым результатам. Наилучший из способов (по

отношению к выбранному критерию - одному или нескольким) называют оптимальным. Приведем

простейший пример такого рода задач.

Пример 1. На некотором предприятии могут выпускать изделия двух видов (например,

мотоциклы и велосипеды). В силу ограниченности возможностей сборочного цеха в нем могут

собирать за день либо 25 мотоциклов (если не собирать вообще велосипеды), либо 100

велосипедов (если не собирать вообще мотоциклы), либо какую-нибудь комбинацию тех и других,

определяемою приемлемыми трудозатратами. Склад может принять не более 70 изделий любого

вида в сутки. Известно, что мотоцикл стоит в 2 раза дороже велосипеда. Требуется найти такой

план выпуска продукции, который обеспечил бы предприятию наибольшею выручку.

676

Такого рода задачи возникают повседневно в огромном количестве, но в реальности число

изделий гораздо больше двух, да и дополнительных условий тоже больше. Решить подобную

задачу путем перебора всех мыслимых вариантов часто невозможно даже на ЭВМ. В нашем

примере, однако, в ЭВМ нет необходимости -задача решается очень легко.

Обозначим число выпускаемых за день мотоциклов х, велосипедов - у. Пусть τ

-время (в

часах), уходящее на производство одного мотоцикла, а τ

- одного велосипеда. Из условия задачи

следует, что τ

= 4τ

. Если завод работает круглосуточно, то, очевидно, при одновременном

выпуске обоих изделий

Но



- число максимально производимых велосипедов, равное 100. Итак, возможности

производства определяют условие

4x + y ≤ 100.

Еще одно условие - ограниченная емкость склада:

x + y ≤ 70

Обозначим цену мотоцикла а

(руб.), цену велосипеда – а

(руб.). По условию а

= 2a

Общая цена дневной продукции

S = а

∙ х + a

∙ у = 2a

∙ х + а

∙ у = а

∙ (2х + у).

Поскольку a

- заданная положительная константа, то наибольшего значения следует

добиваться отвеличины f = 2х + у.

Итак, учитывая все условия задачи, приходим к ее математической модели: среди

неотрицательных целочисленных решений системы линейных неравенств

(7.71)

найти такое, которое соответствует максимуму линейной функции

(7.72)

Проще всего решить эту задачу чисто геометрически. Построим на плоскости (х, у) область,

соответствующую неравенствам (7.71) и условию неотрицательности x и у. Эта область выделена

на рис. 7.62 жирной линией. Всякая ее точка удовлетворяет неравенствам (7.71) и

неотрицательности переменных. Пунктирные линии на рисунке - семейство прямых,

удовлетворяющих уравнению f = 2х + у = с (с разными значениями константы с). Вполне

очевидно, что наибольшему возможному значению f, совместному с предыдущими условиями,

соответствует жирная пунктирная линия, соприкасающаяся с областью М в точке Р.

677

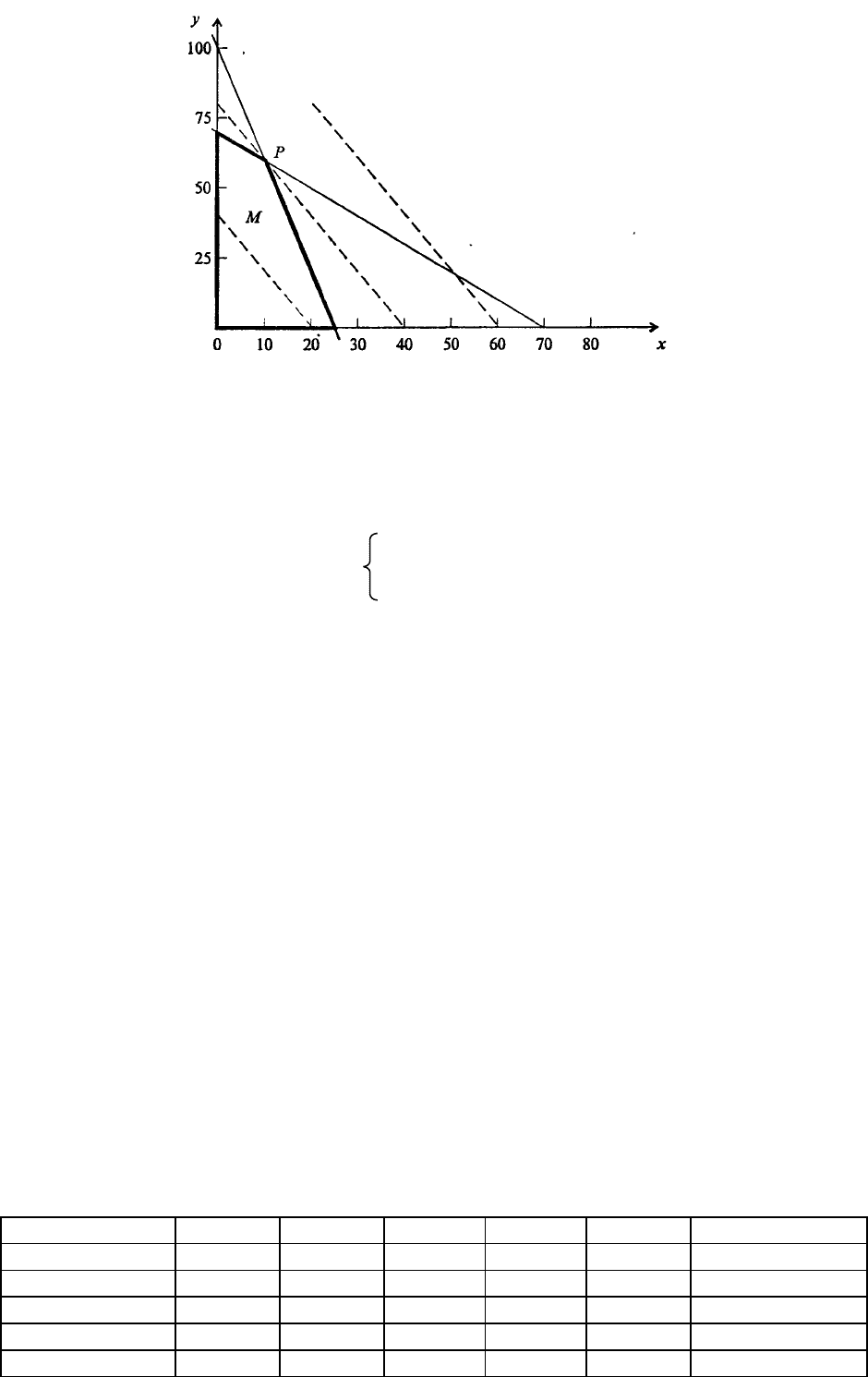
Рис. 7.62. Графическое решение задачи об оптимальном плане производства (к примеру 1)

Этой линии соответствует значение f = 80. Пунктирная линия правее хоть и соответствует

большему значению f, но не имеет общих точек с М, левее - меньшим значениям f. Координаты

точки Р(10, 60) - искомый оптимальный план производства.

Отметим, что нам «повезло» - решение (х, у) оказалось целочисленным. Если бы прямые

4x + y = 100

х + у = 70

пересеклись в точке с нецелочисленными координатами, мы бы столкнулись со значительными

проблемами. Еще больше их было бы, если бы наш завод выпускал три и более видов продукции.

Прежде чем обсуждать возникающие при этом математические проблемы, дадим

формулировки нескольких классических задач линейного программирования в общем виде.

Пример 2. Транспортная задача. Некий продукт (например, сталь) вырабатывается на т

заводах P

, P

, ..., Р

, причем ежемесячная выработка составляетдь а

, a

, …, а

тонн,

соответственно. Пусть эту сталь надо доставить на предприятия Q

, Q

,..., Qk (всего k), причем b

, ..., b

- ежемесячная потребность этих предприятий. Наконец, пусть задана стоимость c

перевозки одной тонны стали с завода Р

на предприятие Q

,. Естественно считать, что общее

производство стали равно суммарной потребности в ней:

+ a

+…+a

= b

+ b

+…+b

(7.73)

Необходимо составить план перевозок, при котором

1) была бы точно удовлетворена потребность в стали предприятий Q

, Q

,..., Q

2) была бы вывезена вся сталь с заводов Р

, Р

,....,P

;

3) общая стоимость перевозок была бы наименьшей.

Обозначим через x

количество стали (в тоннах), предназначенной к отправке с завода Р

на

предприятие Q

. План перевозок состоит из (m∙k) неотрицательных чисел x

(i= 1, 2,..., m;j = 1,2,...,

k).

Таблица 7.10

Схема перевозок стали

в Q

… в Q

Отправлено

из P

… x

из Р

… x

… … … … … … …

из P

… x

Привезено b

… b

678

Первое условие примет вид

(7.74)

Второе условие примет вид

(7.75)

Раз стоимость перевозки одной тонны из Р

в Q

равна c

, то общая стоимость S всех

перевозок равна

(7.76)

Таким образом, мы приходим к следующей чисто математической задаче: дана система

m+k линейных алгебраических уравнений (7.74) и (7.75) c m∙k неизвестными (обычно т∙k >> m+k)

и линейная функция S. Требуется среди всех неотрицательных решений данной системы найти

такое, при котором функция S достигает наименьшего значения (минимизируется).

Практическое значение этой задачи огромно, ее умелое решение в масштабах нашей страны

могло бы экономить ежегодно огромные средства.

Пример 3. Задача о диете. Пусть у врача-диетолога имеется n различных продуктов F

, ..., F

, из которых надо составить диету с учетом их питательности. Пусть для нормального

питания человеку необходимо т веществ N

, N

, ..., N

. Предположим, что за месяц каждому

человеку необходимо γ

кг вещества N

, γ

кг вещества N

, ..., γ

кг вещества N

. Для составления

диеты необходимо знать содержание питательных веществ в каждом продукте. Обозначим через

количество i-го питательного вещества, содержащегося в одном килограмме j-го продукта. Всю

эту информацию представляют в виде, так называемой, матрицы питательности (табл. 7.11).

Таблица 7.11

Матрица питательности

Питательное вещество Продукт

… F

… α

… … … … …

… α

Предположим, что диетолог уже выбрал диету, т.е. определил, что человек должен за месяц

потреблять η

кг продукта F

,..., η

кг продукта F

. Полное количество питательного вещества N

будет

По условию требуется, чтобы его, по крайней мере, хватило

+ η

+…+ η

≥ γ

Точно то же и для остальных веществ. В целом

+ η

+…+ η

≥ γ

(i = 1, 2,… m)

679

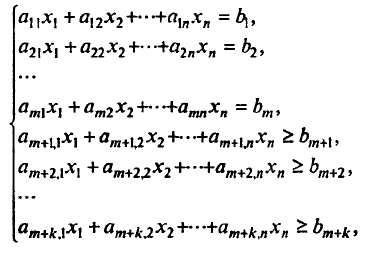
Эти условия определяют наличие минимума необходимых питательных веществ. Диета,

для которой выполнены условия (7.78) - допустимая диета. Предположим, что из всех допустимых

диет должна быть выбрана самая дешевая. Пусть π

- цена 1 кг продукта F

. Полная стоимость

диеты, очевидно,

S = π

+ π

+… + π

. (7.79)

Таким образом, мы пришли к задаче: найти неотрицательное решение η

, …, η

системы

неравенств (7.78), минимизирующее выражение (7.79).

В примерах, приведенных выше. имеется нечто общее. Каждый из них требует нахождения

наиболее выгодного варианта в определенной экономической ситуации. С чисто математической

стороны в каждой задаче требуется найти значение нескольких неизвестных так, чтобы

1) все эти значения были неотрицательны;

2) удовлетворяли системе линейных уравнений или линейных неравенств;

3) при этих значениях некоторая линейная функция имела бы минимум (или максимум).

Таким образом, линейное программирование - это математическая дисциплина, изучающая методы

нахождения экстремального значения линейной функции нескольких переменных при условии,

что последние удовлетворяют конечному числу линейных уравнений и неравенств. Запишем это с

помощью формул: дана система линейных уравнений и неравенств.

Запишем это с помощью формул: дана система линейных уравнений и неравенств

(7.80)

и линейная функция

f = c

+ c

+ … + c

(7.81)

Требуется найти такое неотрицательное решение

≥ 0, x

≥ 0, …, x

≥ 0

системы (7.80), чтобы функция f принимала наименьшее (или наибольшее) значение.

Условия (7.80) называют ограничениями данной задачи, а функцию f - целевой функцией

(или линейной формой). В приведенных выше примерах ограничения имели вид не уравнений, а

неравенств. Заметим, что ограничения в виде неравенств всегда можно свести к системе в виде

равенств (способом введения добавочных неизвестных).

Так, для неравенства

+ a

+ … + a

≥ b

вводя добавочное неизвестное x

n +1

, получаем

n+1

= a

+ a

+ … + a

- b

Потребовав его неотрицательности наряду с остальными неизвестными, получим, что

условие x

n + 1

≥ 0 превращает (7.84) в (7.83). Введя по отдельному дополнительному неизвестному

для каждого из неравенств, получим систему уравнений, равносильную исходной системе

неравенств. Пример. Дана система неравенств

680